KSEEB SSLC Class 10 Maths Solutions Chapter 2 Triangles Ex 2.3 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 2 Triangles Exercise 2.3.
Karnataka SSLC Class 10 Maths Solutions Chapter 2 Triangles Exercise 2.3
Question 1.
State which pairs of triangles In the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
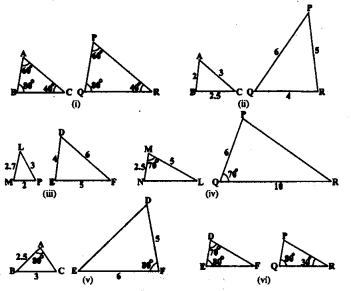
Solution:
(i)
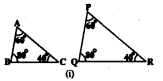
In ∆ABC and ∆PQR,
∠A = ∠P = 60°
∠B=∠Q = 80°
∠C =∠R = 40°
∴ SimilarIty criterion of two triangles is A.A.A.
∴ ∆ABC ~ ∆PQR.
(ii)
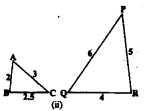
In ∆ABC and PQR, we have
\(\frac{A B}{Q R}=\frac{B C}{P R}=\frac{A C}{P Q}=\frac{1}{2}\)
i.e., sides of one triangle are proportional to the sides of the other triangle.
∴SImilarity criterion is S.S.S.
∴ ∆ABC ~ ∆PQR.
(iii)
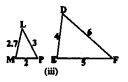
∆LMP and ∆DEF are not similar triangles because one pair of sides are not proportional to each other.
\(\quad \frac{\mathrm{MP}}{\mathrm{DE}}=\frac{\mathrm{LP}}{\mathrm{DF}}=\frac{2}{4}=\frac{3}{6}=\frac{1}{2}\)
But, \(\frac{\mathrm{LM}}{\mathrm{EF}}=\frac{2.7}{5} \neq \frac{1}{2}\)
∴ These are not similar triangles
(iv)
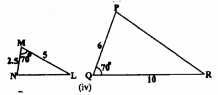
In ∆MNL and ∆PQR, we have
∠M = ∠Q = 70°
But, \(\frac{\mathrm{MN}}{\mathrm{PQ}} \neq \frac{\mathrm{ML}}{\mathrm{QR}}\)
∴ These are not similar triangles
(v)
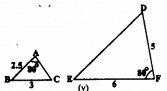
In ∆ABC and ∆DEF, we have
\(\frac{A B}{D F}=\frac{B C}{E F}=\frac{1}{2}\)
∠A = ∠F = 80°
∴ Similarly criterion for these triangles is S.A.S
∴ ∆ABC ~ ∆DEF
(vi)
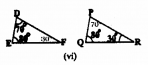
Sum of three angles of is 180°, but in ∆DEF. sum of two angles. ∠F= 30°. In ∆PQR, ∠P = 70°.
In ∆DEF and ∆PQR. we have
∠D = ∠P = 70°
∠E =∠R = 80°
∠F = ∠R = 30°
∴ Three angles of these triangles are equal to each other.
∴ SimIlarity criterion here is A.A.A.
∴ ∆DEF ~ ∆PQR.
Question 2.
In the following figure. ∆OBA ~ ∆ODC, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
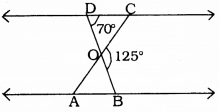
Solution:
∆OBA ~ ∆ODC (data)
In ∆OBA and ∆ODC, we have
∠ODC = ∠OBA = 70° (. Alternate angle)
∠AOB = 180°- 125° = 55° ( Adjacent angle)
∴ ∠AOB = ∠DOC = 55° (: VertIcally opposite angles)
∠OAB = ∠OCD = 55° (. Alternate angles)
∴ ∠DOC=55°
∠DCO = 55%
∠OAB= 55%.
Question 3.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)
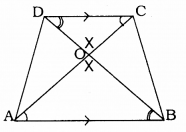
Solution:
Data: Diagonals AC and BD of a trapezium ABCD with AB || DC. intersect each other at the point O.
To Prove: \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)
In the trapezium ABCD AB || DC.
∴ ∠OCD = ∠OAB (Alternate angles)
∠ODC = ∠OBA (Alternate angles)
∠DOC = ∠AOB (Vertically opposite angles)
∴ These are equlangular triangles.
∴ These triangles are similar.
∴ ∆ODC ~ ∆OAB
\(\quad \frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)
∵ Corresponding sides are in proportional.
Question 4.
In the following figure. \(\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{PR}}\) and ∠1 = ∠2. Show that ∆PQS ~ ∆TQR.
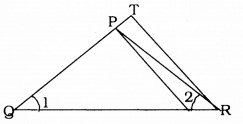
Solution:
Data: Here \(\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{PR}}\)and ∠1 = ∠2
To prove: ∆PQS ~ ∆TQR.
In ∆PQS and ∆TQR, we have
\(\frac{\mathrm{Q} \mathrm{R}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{PR}}\)
∠PQR = ∠PRQ (∵ ∠1 = ∠2)
Here, Similarity criterion used here is side, angle, side (SAS).
∴ ∆PQS ~ ∆TQR.
Question 5.
S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
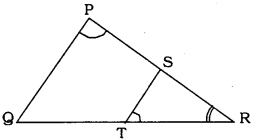
Solution:
Data: S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS.
To Prove: ∆RPQ ~ ∆RTS.
In ∆RPQ and ∆RTS,
∠P = ∠RTS (Data)
∠PRQ = ∠SRT (Common)
∴ 3rd angle ∠PRQ = ∠SRT
∴ These are equiangularangular triangles.
∴ Here A.A.A. similarity criterion.
∴ ∆RPQ ~ ∆RTS.
Question 6.
In the given fIgure. ∆ABE ≅ ∆ACD. show that ∆ADE ~ ∆ABC.
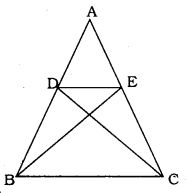
Solution:
Data: ∆ABE ≅ ∆ACD.
To Prove: ∆ADE ~ ∆ABC.
∆ABE ≅ ∆ACD
AB = AC
AD = AE.
Then DC = BE
AB = AC
AD + DB = AE + EC
∴ DB = EC
(∵ DA = AE)
In ∆ADE and ∆ABC,
\(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{\mathrm{DE}}{\mathrm{BC}}\)
Here, corresponding sides are in proportion.
∴ Similarity criterion for ∆ is side, side, side
∴ ∆ADE ~ ∆ABC
Question 7.
In following figure. altitudes AD and CE of ∆ABC Intersect each other at the point P. Show that:
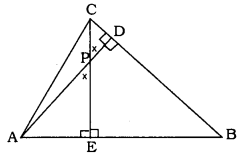
i) ∆AEP ~ ∆CDP
ii) ∆ABD ~ ∆CBE
iii) ∆AEP ~ ∆AÐB
iv) ∆PDC ~ ∆BEC.
Solution:
Data: altitudes AD and CE of ABC
Intersect each other at the point P.
To Prove: i) ∆AEP ~ ∆CDP
ii) ∆ABD ~ ∆CBE
iii) ∆AEP ~ ∆ADB
iv) ∆PDC ~ ∆BEC
i) In ∆AEP and ∆CDP.
∠AEP = ∠CDP = 90° (data)
∠APE = ∠CPD (Vertically opposite angle)
∴ ∠PAE = ∠PCD
These are equiangular triangles.
Similarity criterion for ∆ is A.A.A
∴ ∆AEP ~ ∆CDP
(ii) In ∆ABD and ∆CBE.
∠ADB = ∠CEB = 90° (data)
∠ABD = ∠CBE (common)
∴ ∠DAB = ∠BCE
These are equiangular triangles.
∴ Similarity criterion for is A.A.A.
∴ ∆ABD ~ ∆CBE
(iii) In ∆AEP and ∆ADB.
∠AEB = ∠ADB = 90° (data)
∠PAE = ∠DAB (common)
∴ ∠APE = ∠ABD.
∴ These are equiangular triangles.
∴ Similarity criterion for is A.A.A.
∴ ∆AEP ~ ∆ADB
(iv) In ∆PDC and ∆BEC.
∠PDC = ∠BEC = 90° (data)
∠PCD = ∠BCE (common)
∴ ∠CPD = ∠CBE
∴ These are equiangularangular triangles.
Similarity criterion for ∆ is A.A.A.
∴ ∆PDC ~ ∆BEC.
Question 8.
E is a point on the side AD produced of a parallelogram ABCD and BE Intersects CD at F. Show that ∆ABE ~ ∆CFB.
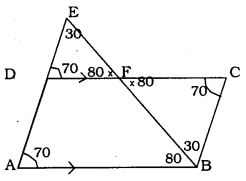
Solution:
Data: E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F.
To Prove: ∆ABE ~ ∆CFB
In \(\) ABCD Adjacent angles are equal.
Let ∠DAB = ∠BCD = 70°
∠DAB = ∠EAF = 70° (∵ Corresponding angle)
In ∆EDF, ∠DEF = 30° then,
∠EFD = 80°.
∠EFD = ∠BFC = 80° (vertIcally opposite angles)
In ∆FBC, ∠FBC = 30°. ,
Now in ∆ABE and ∆CFB,
∆EAB = ∆BCF = 70°
∆AEB = ∆FBC = 30°
∆ABE = ∆BFC = 80°
∴ Similarity criterion for ∆ is A.A.A.
∴ ∆ABE ~ ∆CFB
Question 9.
In the given figure. ∆ABC and ∆AMP are two right triangles, right angled at B and M respectively. Prove that:
i) ∆ABC ~ ∆AMP
ii) \(\frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}\)
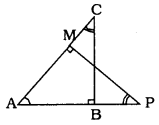
Solution:
Data: ∆ABC and ∆AMP are two right triangles, right angled at B and M respectvely.
To Prove: i) ∆ABC ~ ∆AMP
ii) \(\frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}\)
(i) In ∆ABC and ∆AMP,
∠ABC = ∠AMP = 90° (data)
∠CAB = ∠MAP (common)
∴ ∠ACB = ∠MPA
∴ These are equiangular triangles.
Similarity criterion for ∆ is A.A.A.
∴ ∆ABC ~ ∆AMP
(ii) ∆ABC ~ ∆AMP(Proved)
∴ Corresponding sides are in proportion.
LC and LP are corresponding angles.
∴ Adjacent sides are CA, PA.
Similarly BC and MP are adjacent sides.
\(\quad \frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}\)
Question 10.
CD and OH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively.
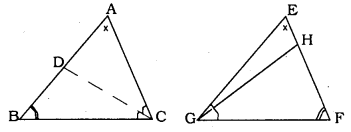
If ∆ABC ~ ∆EFG, show that
i) \(\frac{C D}{G H}=\frac{A C}{F G}\)
ii) ∆DCB ~ ∆HGE
iii) ∆DCA ~ ∆HGF
Solution:
Data : CD and OH are respectively the bisectors of ∠ACB and ∠EGF such that D and H 11e on sides AB and FE of ∆ABC and ∆EFG respectively.
∆ABC ~ ∆EFG
To Prove: i) \(\frac{C D}{G H}=\frac{A C}{F G}\)
ii) ∆DCB ~ ∆HGE
iii) ∆DCA ~ ∆HGF
Proof: ∆ABC ~ ∆EFG (data given)
∴ Their corresponding sides are in proportion.
\(\quad \frac{\mathrm{AB}}{\mathrm{EF}}=\frac{\mathrm{BC}}{\mathrm{FG}}=\frac{\mathrm{AC}}{\mathrm{EG}}\)
∠B = ∠F, ∠A = ∠E, ∠C = ∠G.
(i) In ∆ADC and ∆EHG,
∠A = ∠E .
∠ACD = ∠EGH
∴ Their sides are in proportion.
\(\frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}}\)
(ii) In ∆DCB and ∆HGE.
\(\frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{BC}}{\mathrm{GF}}\)
∴ ∆DCB ~ ∆HGE
(iii) In ∆DCA and ∆HGE,
\(\frac{\mathrm{DC}}{\mathrm{GH}}=\frac{\mathrm{AD}}{\mathrm{EH}}=\frac{\mathrm{AC}}{\mathrm{EG}}\)
∴ ∆DCA ~ ∆HGE
Question 11.
In the following figure. E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ∆ABD ~ ∆ECF
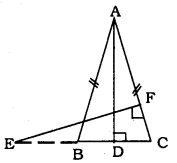
Solution:
Data: E Is a point on side CB produced of an isosceles ∆ABC with AB = AC. AD ⊥ BC and EF ⊥ AC,
To Prove: ∆ABD ~ ∆ECF
In ∆ABD and ∆ECF.
∠ADB = ∠EFC = 90° (data)
∠ABD = ∠FCE (∵ ∠B = ∠C)
∠BAD = ∠FEC
∴ Equiangular triangles.
∴ Similarity criterion for triangles is A.A.A.
∴ ∆ABD ~ ∆ECF.
Question 12.
Sides AB and BC and median AD of a ¿ABC are respectively proportional to sides PQ and QR and median PM of ∆PQR. (Sec figure gIven below) Show that ∆ABC ~ ∆PQR
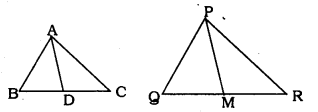
Solution:
Data: Sides AB and BC and median AD of a ∆ABC are respectively proportional to sides P9 and QR and medIan PM of ∆PQR.
To Prove: ∆ABC ~ ∆PQR
In ∆ABC and ∆PQR,
Side \(\frac{\mathrm{AB}}{\mathrm{PG}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
D is the mid-point of BC
∴ BD = DC
M is the mid-point of QR.
∴ QM = MR.
In ∆ADC and ∆PMR,
\(\frac{\mathrm{AD}}{\mathrm{PM}}=\frac{\mathrm{DC}}{\mathrm{MR}}=\frac{\mathrm{AC}}{\mathrm{PR}} \quad \left(\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\frac{1}{2} \mathrm{BC}}{\frac{1}{2} \mathrm{QR}}\right)\)
Similarity criterion is S.S.S.
∴ ∆AÐC ~ ∆PMR
Now, In ∆ABC and ∆PQR.
\(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\)
∴ SimilarIty criterion is S.S.S.
∴ ∆ABC ~ ∆PQR.
Question 13.
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
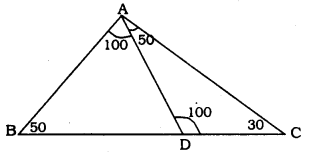
Solution:
Data: D is a point on the side BC of a triangle ∆ABC such that ∠ADC = ∠BAC.
To Prove: CA2 = CB × CD
Let ∠ADC = ∠BAC = 100°
In ∆ABC, If ∠B = 50°,then ∠C = 30°
In ∆ADC, If ∠C = 30°. then ∠DAC = 50°
In ∆BCP, ∠A= 100°, ∠B= 50°, ∠C= 30°
In ∆ADC, ∠ADC = 100. ∠DAC = 50°.
∠ACD = 30°
Similarity criterion of ∆ is A.A.A.
∴ In ∆ABC and ∆ADC,
\(\frac{\mathrm{CA}}{\mathrm{BC}}=\frac{\mathrm{DC}}{\mathrm{CA}}\)
∴ CA × CA = BC × DC
∴ CA2 = BC × DC.
Question 14.
Sides AB and AC and median AD of a triangle ∆ABC are respectively proportional to sides PQ and PR and mediam PM of another triangle ∆PQR. Show that ∆ABC ~ ∆PQR.
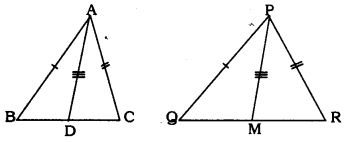
Solution:
Data: Sides AB and AC and median AD of a triangle ∆ABC are respectively proportional to sides PQ and PR and medIan PM of another triangle ∆PQR.
To Prove: ∆ABC ~ ∆PQR
In ∆ABC and ∆PQR
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
Corresponding sides are proportional.
Similarity criterion for ∆ is S.S.S
∴ ∆ABC ~ ∆PQR.
Question 15.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
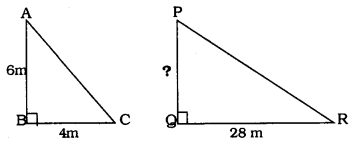
Solution:
Height of PQ =?
In ∆ABC and ∆PQR,
∠B = ∠Q = 90°
∴ Hypotenuse AC is proportional to PQ
\(\quad \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{MR}}=\frac{\mathrm{AC}}{\mathrm{PR}}\)
\(\frac{6}{\mathrm{PQ}}=\frac{4}{28}\)
∴ 4 × PQ = 6 × 28
\(\quad \mathrm{PQ}=\frac{6 \times 28}{4} \quad \quad \mathrm{PQ}=42 \mathrm{m}\)
Question 16.
If AD and PM are medians of triangles ∆ABC and ∆PQR respectively, where ∆ABC ~ ∆PQR. prove that \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
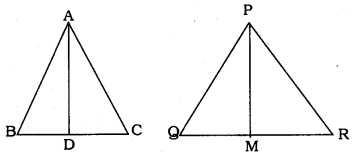
Solution:
Data : AD and PM are medians of triangles ∆ABC and ∆PQR respectively. ∆ABC ~ ∆PQR.
To Prove: \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
∆ABC ~ ∆PQR.(data)
∴ we have \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{BC}}{\mathrm{QR}}\)
D is the mid-point of BC. BD = DC.
M Is the mid-point of QR. QM = MR
\(\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\frac{1}{2} \mathrm{BC}}{\frac{1}{2} \mathrm{QR}}=\frac{\mathrm{BD}}{\mathrm{QM}}\)
\(\quad \frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{BD}}{\mathrm{QM}}\)
In ∆ABD and ∆PQM, we have
\(\quad \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BD}}{\mathrm{QM}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
\(\quad \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 2 Triangles Ex 2.3 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 2 Triangles Exercise 2.3, drop a comment below and we will get back to you at the earliest.