Students can Download Karnataka SSLC Maths Model Question Paper 1 with Answers, Karnataka SSLC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus SSLC Maths Model Question Paper 1 with Answers
Time: 3 Hours
Max Marks: 80
I. In the following questions, four choices are given for each question, choose and write the correct answer along with its alphabet: ( 1 × 8 = 8 )
Question 1.
The pair of linear equations 3a + 4b = k, 9a + 12b = 6 have infinitely many solutions when,
a) K = -2
b) K = 3
c) K = 2
d) K = -3
Answer:
c) K = 2
Question 2.
The HCF and LCM of 12, 15 and 21 are ________ and ________ respectively
a) 3,1
b) 420,3
c) 3, 420
d) 420,1
Answer:
c) 3,420
Solution:
Factors of 12 = 2 × 2 × 3
= 3 × 5
= 7 × 3
![]()
Question 3.
The value of \(\frac{\sin 18}{\cos 72}\) is ________
a) 1 / 2
b) 1
c) 0
d) √3 / 2
Answer:
b) 1
Solution:

Question 4.
The distance between the points p(2, 3) and Q(4, 1) is
a) 3√6
b) 2√2
c) 2√4
d) 3√9
Answer:
b) 2√2
Solution:

Question 5.
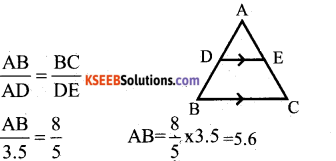
In the given figure^ABC, DE||BC. If DE=5cm, BC=8cm and AD=3.5 cm, then the length of AB is
a) 5.6cm
b) 4.8cm
c) 5.2cm
d) 6.4 cm
Answer:
a) 5.6cm
Solution:
Question 6.
6. The 10th term of an A.P : 2, 7, 12,
a) 1
b) 47
c) 9
d) 17
Answer:
b) 47
Solution:
a = 2, d= 7 – 2 = 5, ri= 10
an = a + (n – 1)d
= 2 + (10-1) (5)
= 2 + 45 = 47
∴ 10th term of an AP is 47.
![]()
Question 7.
A box consists, of 4 red, 5 black and 6 white balls. One ball is drawn out at random, find the probability that the ball drawn is black.
a) 1/15
b) 1
c) 1/4
d) 1/3
Answer:
d) 1/3
Solution:

Question 8.
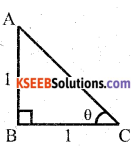
In the given fig, the angle of elevation θ is
a) 30°
b) 45°
c) 90°
d) 60°
Answer:
b) 45°
Solution:
Tan θ = \(\frac{A B}{B C}=\frac{1}{1}\)
Tan θ = Tan 45°
θ = 45°
II. Answer the following Questions : ( 1 × 8 = 8 )
Question 9.
7 × 11 × 13 + 13 is a composite number. Why?
Answer:
7 × 11 × 13 + 13 = 1014 is a number divisible by some other numbers other than itself and by one.
∴ 1014 is a composite number.
Question 10.
If one of the roots of the quadratic equation 6x2 – x – 2 = 0 is 2/3. Find the other.
Answer:
Let a and p are the roots.

![]()
Question 11.
Find the Value of cos90° + tan 45° Soln: cos90 + tam45 = 0+1 = 1
Answer:
cos 90 + tan 45 = 0 + 1 = 1
Question 12.
If F(2, P) is the mid point of the Sine segment joining the points A(6, -5) and B(-2, 11). Find the value of P.
Answer:
Since P is the mid point of AB,
Co – ordinates of P are


Co – ordinates of P are (2, 3)
Question 13.
If the probability of winning a game is 5/11, what is the probability of losing it.
Answer:
PE(E) + P(Ē) = 1
\(\frac{5}{11}\) + P(Ē) = 1
P(Ē) = 1 – \(\frac{5}{11}\) = 1 – \(\frac{5}{11}\)
∴ P(Ē) = \(\frac{6}{11}\)
Question 14.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then the what is the measure of ∠POA = ?
Answer:
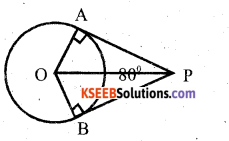
In ∆ POA , ∠OAP = 90°
∠APO = y = 40
∠POA = 90 – 40 = 50°
∴ ∠POA = 50°
Question 15.
Write the formula to find the volume of a hemisphere.
Answer:
Volume of hemisphere = 2/3 πr3
Question 16.
What is the Area of the shaded region?
Answer:
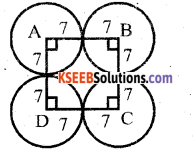
Area of the shaded region = Area of square – Area of circle
= (14)2 \(\frac{22}{7}\) × 7 × 7
= 196 – 154
= 42 sq.cms .
III. Answer the following : ( 2 ×8 = 16 )
Question 17.
P.T 5 – √3 is irrational.
Answer:
Let 5 – √3 be rational no. in the form of p/q
where p and q are integers and q ≠ 0.
5 – √3 = p/q
5 = \(\frac{p}{q}+\sqrt{3}\)
⇒ 5 is rational number, \(\frac{p}{q}+\sqrt{3}\) is irrational which leads to the contradiction.
Hence our assumption is wrong.
5 – √3 is not a rational number ,
⇒ 5 – √3 is an irrational number.
Question 18.
In the figure DE || AC and DF || AE. BF BE
Prnvp that = \(\frac{\mathbf{B F}}{\mathbf{F E}}=\frac{\mathbf{B E}}{\mathbf{E C}}\)
Answer:
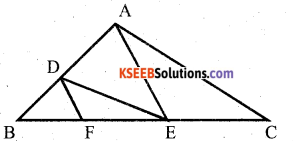
By Thales theorem,
In ∆ ABC, DE || AC


OR
In fig LM || CB and LN || CD Prove that \(\frac{A M}{A B}=\frac{A N}{A D}\)
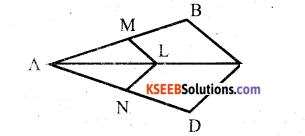
Answer:
In ∆ ABC
LM || CB
According to Thales theorem,
\(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AL}}{\mathrm{AC}}\) ….. (1)
In ∆ ADC LN || CD
According to corollary of Thales
\(\frac{A N}{A D}=\frac{A L}{A C}\) ……. (2)
From (1) and (2)
\(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\)
Question 19.
On comparing the ratios \(\frac{\mathbf{a}_{1}}{\mathbf{a}_{2}}, \frac{\mathbf{b}_{1}}{\mathbf{b}_{2}}\) and \(\frac{\mathbf{c}_{1}}{\mathbf{c}_{2}}\) find out whether the lines representing the following pair of linear equations interesect at a point, are parallel or coincident
5x – 4y + 8 = 0
7x + 6y – 9 = 0
5x – 4y + 8 = 0 is the line a1x + b1y + C1 = 0
7x + 6y – 9 = 0 is the line a2x + b2y +c2 =0
a1 = 5, b1 = -4, c1 = 8
a2 = 7, b2 = 6, c2 = -9
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) The two lines are intersecting lines.
![]()
Question 20.
Draw a circle of radius 4cm and construct a pair of tangents to the circle from a point 8cm away from the centre.
Answer:
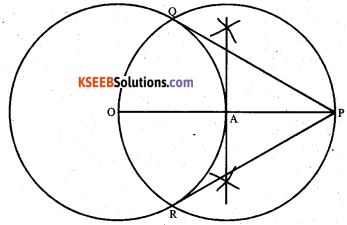
Question 21.
Find a quadratic polynomial, the sum and product of whose zeroes are -3 and 2 respectively.
Answer:
Let the quadratic polynomial be ax2 + bx + c and its zeroes be α and β
α + β = -b/a = -3
αβ = c/a = 2
Equation is x2 – ( α + β) x + αβ
x2 – (-3)x + 2
x2 + 3x + 2
Question 22.
A kite is flying at a height of 60m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that is no slack in the string.
Answer:
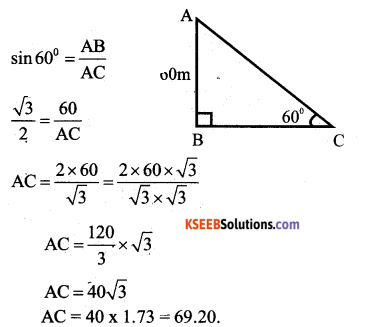
OR
Two solid right circular cones have same height and the radii of bases are r1 and r2. Both the cones are metled and recasted to form a cylinder of same height. Show that the radius of the base of the cylinder is \(\sqrt{\frac{\mathbf{r}_{1}^{2}+\mathbf{r}_{2}^{2}}{3}}\)
Answer:
Volume of the cylinder = Sum of the volumes 2 cones

Question 23.
A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Answer:
Distance covered by the wheel in one revolution = Distance moved / Number of revolutions
= \(\frac{11}{5000}\) cm
= \(\frac{11}{5000}\) × 1000 × 100cm
= 220cm
∴ Circumference of the wheel = 220 cm
2πr = 220cm
= 2 × \(\frac{22}{7}\) × r
= 220
=3- r = 35 cm
∴ Diameter = 2r = 2 × 35 = 70cm
Hence, the diameter of the wheel = 70cm.
Question 24.
A conical vessel whose internal radius is 5cm and height 24cm is full of water. The water is emptied into a cylindrical vessel with internal radius lOcms. Find the height to which the water rises.
Answer:
r1 = radius o the conical vessel = 5cm
h1 = height of the conical vessel = 24cm
r2 = radius of the cylindrical vessel = 10cm.
∴ Volume of water in conical vessel = Volume of water in cylindrical vessel.

∴ Height of the water in the cylindrical vessel = 2cm.
III. Answer the following : ( 3 × 9 = 27 )
Question 25.
If 2 is added to numerator and denominator to a fraction, it becomes 9/10 If 3 is subtracted from numerator and denominator, the fraction becomes 4/5 Find the function.
Answer:
Let the fraction be x / y
where x < y
If 2 is added to Nr and Dr, we get 9/10
∴ \(\frac{x+2}{y+2}=\frac{9}{10}\)
10(x + 2) = 9(y + 2)
10x + 20 = 9y + 18
10x – 9y + 20 – 18 = 0
10x – 9y + 2 = 0
l0x – 9y = -2 ..(1)
If 3 is subtracted from same fraction, we
\(\frac{x-3}{y-3}=\frac{4}{5}\)
5(x – 3) = 4(y – 3)
5x – 15 = 4y – 12
5x – 4y = -12 + 15
5x – 4 = 3….. (2)
Solve (1) and (2)
(10x – 9y = -2) x 5
(5x – 4y = 3) x 10
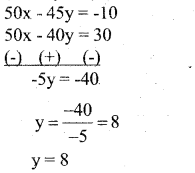
Substitute the value of y in (1)
10x – 9y = -2
10x – 9(8) = -2
10x – 72 = -2
10x = -2 + 72
10x = 70
x = 7
∴ Fraction = \(\frac{x}{y}=\frac{7}{8}\)
OR
A girl is twice as old as her sister. Four years, hence the product of their ages (in years) will be 160. Find their
present ages.
Answer:
Let Girls present age be x years.
Sister’s age = 2x years.
After 4 years, their respective ages will be (x + 4) years and (2x + 4) years.
(x + 4) (2x + 4) =160
2x2 + 4x+ 8x + 16= 160
2x2 + 12x+ 16= 360
x2 + 6x + 8 = 80
x2 + 6x + 8 – 80 = 0
x2 + 6x – 72 = 0
x2+ 12x – 6x – 72 = 0
x(x + 12) – 6(x + 12) = 0
(x + 12) (x – 6) = 0
x + 12 = 0
x = -12 or x – 6 = 0, x = 6.
Girls present age = 6 years.
Sister’s age = 12 years.
![]()
Question 26.
The difference of squares of two natural numbers is 84. The square of the larger number is 25 times the smaller number. Find the numbers.
Answer:
Let the two natural numbers be x and y such that x > y.
x2 – y2 = 84 ……..(1)
x2 = 25y …….(2)
By eq.(1) and (2)
25y – y2 = 84
y2 – 25y + 84 = 0
y2 – 21y – 4y + 84 = 0
y (y – 21) – 4(y – 21) = 0
(y – 21) (y – 4) = 0
y – 21 = 0,y = 4
Substitute the value of y in (2)
x2 = 25 x 21
x = \(\sqrt{25 \times 21}=5 \sqrt{21}\)
x2 = 25y
x2 = 25 × 4= 100
x = √10o = 1o
∴ Two numbers are 10 and 4.
Question 27.
Find the value of K if the points A(2, 3) B (4, k) and C(6, -3) are collinear.
Answer:
Since the given points are collinear, the area of the triangle formed by them must be O.
\(\frac{1}{2}\)[2(k + 3) + 4(-3 -3) + 6(3 – k)] = 0 1
\(\frac{1}{2}\)[2k + 6 + 4(-6) + 6(3 – k)] = 0
\(\frac{1}{2}\)[2k + 6 – 24 + 18 – 6k] = 0
\(\frac{1}{2}\)(-4k) = 0
-2k = 0 or k = 0.
OR
Find the area of a triangle whose vertices are (1, -1) (-4, 6) and (-3, -5)
Answer:
Area of the triangle =
= \(\frac{1}{2}\)[x1(y2 – y3) + x2 (y3 – y2) + x3 (y1 – y2)]
x1 = 1 x2 = -4 x3 = -3
y1 = -1 y2 = 6 y3 = -5
Area = \(\frac{1}{2}\)[1(6 + 5) + (-4) (-5 + 1) + (-3)(-l- 6)]
= \(\frac{1}{2}\) [11 + (-4(-4) +(-3) (-7)]
= \(\frac{1}{2}\) (11 + 16 + 21)
= \(\frac{1}{2}\) (48) = 24 .
∴ Area of the triangle = 24 square units.
Question 28.
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
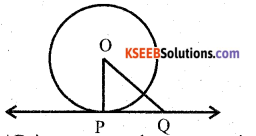
Answer:
Given
centred ‘O’ at the point of contact ‘P’.
To Prove that : OP ⊥ AB
Construction : Take any point Q, other than P, on the tangent AB, Join OQ, OQ cuts the circle at R.
Proof : “Of all the line segments joining the point ‘O’ to the tangent AB, perpendicular OP is the shortest distance from O to AB.
∴ OP = OR [ Radii of the same circle]
OQ = OR + RQ .
OQ > OR
OQ > OP (∵ OP = OR)
OP > OQ
∴ ‘OP’ is the shortest distance from point O to AB.
OP ⊥ AB
Question 29.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44cm, each bullet being 4cm in diameter.
Answer:
d = 4cm, r = 2cm, a = 44cm.
Volume of cube = a3 = 443cm3.

OR
A circus tent is cylinderica! upto a height of 3m and conical above it. If the diameter of the base is 105m and the slant height of th conial part is 53m, find the total canvas used in making the tent.
Answer:
d= 105m, r = 105/2 = 52.5m, l = 53m,
h = 3m.
Total canvas used = C.S.A of cylinder + C.S.A. of cone
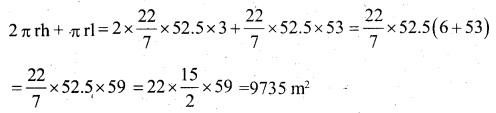
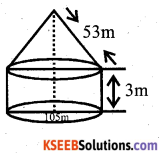
Question 30.
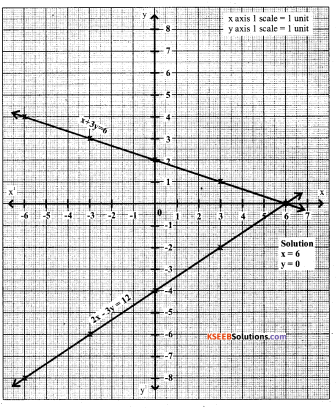
Solve the following system of equations graphically.
x + 3y = 6
2x – 3y = 12
Answer:
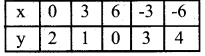
x + 3y = 6
3y = 6- x
y = \(\frac{6-x}{3}\)
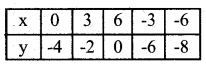
2x – 3y = 12
-3y = 12 – 2x
3y = 2x – 12
y = \(\frac{2 x-12}{3}\)
![]()
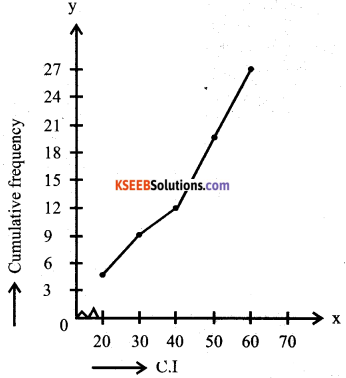
Question 31.
Draw less than Ogive for the given data:

Answer:
| C.I | F | C.f |
| 20- 30 | 5 | 5 |
| 30-40 | 4 | 9 |
| 40-50 | 3 | 12 |
| 50-60 | 8 | 20 |
| 60-70 | 7 | 27 |
Question 32.
How many terms of the series 54, 51, 48…. be taken. So that their sum is 513? Find the last term.
Answer:
n = ? a = 54, d = 51 – 54 = -3, Sn = 513. S„=
Sn\(\frac{\mathrm{n}}{2}\) [2a + (n-1)d]
513 = \(\frac{\mathrm{n}}{2}\) [2(54) + (n – 1)(-3)]
513 = \(\frac{\mathrm{n}}{2}\) (l08-3n + 3)
n(111 -3n)= 1026
111n – 3n2 – 1026 = 0
-3n2 + 111n- 1026 = 0
Divide by -3.
n2-37n + 342 = 0
n2 – 19n – 18n + 342 = 0
n(n – 19) – 18(n -19) = 0
(n – 19) (n – 18) = 0
∴ n = 19 or n = 18
T19 = a + 18d
= 54-54 =54-51
T19 = 0
OR
T18 = a + 17d
= 54 + 18(-3)
= 54 + 17(-3)
T18 = 3
∴ Sum of 18termsas well as that of 19 terms is 513.
Question 33.
The sum of two numbers is 15. If the sum of their reciprocals is 3/10. Find the numbers.
Answer:
Let the numbes be x and (15 – x)
By data,
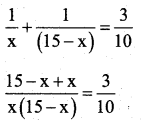
45x – 3x2 = 150
3x2 – 45x + 150 = 0
Divide by 3 .
x2 – 45x + 150=0
Divide by 3
x2 – 15x + 50 = 0
x2 – 10x – 5x + 50 = 0
x(x – 10) – 5(x – 10) = 0
(x – 10) (x – 5) = 0
x -10 = 0
x = 10 OR
x – 5 = 0
x = 5
Hence the two numbers are 10 and 5.
OR
Seven years ago Keshav’s age was five times the square of Raghav’s age. Three years hence Raghav’s age will be two fifth of Keshav’s age. Find their present ages.
Answer:
Seven years ago, let Raghav’s age be x years. Then, seven years ago Keshav’s age was 5x2 years.
Raghav’s present age = (x + 7) years.
Keshav’s present age = (5x2 + 7) years.
Three years hence, we have R
aghav’s age = (x + 7 + 3) years = (x + 10) years.
Keshav’s age = (5x2 + 7 + 3) years = (5x2 +10) years.
It is given that three years hence Raghav’s 2
age will be 2/5 of Keshav’s age.
x + 10 = \(\frac{2}{5}\) (5x2 +10)
x + 10 = 2x2 + 4
2x2 + 4-x – 10 = 0
2x2 – 6 – x = 0
2x2 – 4x + 3x – 6 = 0
2x(x – 2) + 3(x – 2) = 0 ,
(x – 2) (2x + 3) =0
x – 2 = 0, 2x + 3 = 0
x = 2, x = -3/2
Raghav’s present age = (2 + 7) years = 9 years.
Keshav’s present age = (5 x 22 + 7) = 27 years.
![]()
V. Answer the following : ( 4 × 4 = 16 )
Question 34.
The first and the last term of an A.P are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum? Soln: Let a be the first term and d be the common difference.
Answer:
Let 1 be its last term. Then a = 17,1 = an =350 and d = 9
1 = an = 350 ”
a + (n – 1)d = 350
9(n – 1) = 350 – 17 = 333
n – 1 = 333/9 = 38
n = 37 + 1 = 38
Putting a = 17,1 = 350 and n = 38
Sn = \(\frac{n}{2}\) (a + 1)
S38 = \(\frac{38}{2}\) (17 + 350) .
= 19 × 367
= 6973
Hence, there are 38 terms in A.P having their sum as 6973.
OR
Find the sum of first 51 terms of an A.P whose 2nd term and 3rd term are 14 and 18 respectively.
Answer:
Let a be the first term and d be the common difference of given A.P. Then
a2= 14 and a3 = 18 a + d = 14 and a + 2d = 18
Solve
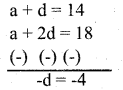
d= 4
a + d= 14
a + 4 = 14
a = 14 – 4 = 10
a = 10
Putting a = 10, d = 4 nd n = 51
Sn = \(\frac{n}{2}\) [2a + (n-l)d]
S5l= \(\frac{51}{2}\)[2×10 + (51 – 1) × 4]
= \(\frac{51}{2}\)[20 + 50 × 4]
= \(\frac{51}{2}\)(20 + 200)
= \(\frac{51}{2}\) × 220
= 51 × 110= 5610
Question 35.
Find the mean for the following data

Answer:

![]()
Question 36.
Prove the Identity
\(\frac{\tan ^{2} \theta}{\sin ^{2} \theta-1}+\frac{\csc ^{2} \theta}{\sec ^{2} \theta-\csc ^{2} \theta}=\frac{1}{\sin ^{2} \theta-\cos ^{2} \theta}\)
Answer:
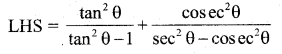

Question 37.
Construct a triangle with sides 5cm. 6cm and 7cm and then another triangle
whose sides are 7/5 of the corresponding sides of the first triangle.
Answer:
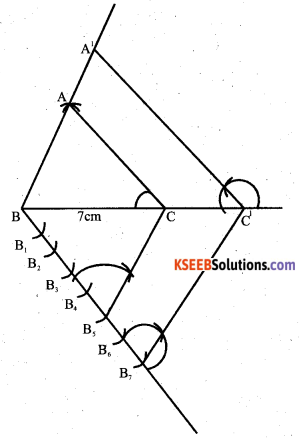
VI. Answer the following : ( 5 × 1 = 5 )
Question 38.
Areas of similar triangles are proportional to the squares on the corresponding sides.
Answer:
Areas of similar triangles are proportional to the squares on the corresponding sides.
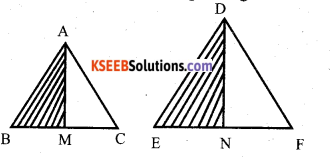
Data: ∆ ABC ∆DEF
∠A = ∠D
∠B = ∠F
∠C = ∠F
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{EF}}\)
