KSEEB SSLC Class 10 Maths Solutions Chapter 13 Statistics Ex 13.4 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 13 Statistics Exercise 13.4.
Karnataka SSLC Class 10 Maths Solutions Chapter 13 Statistics Exercise 13.4
Question 1.
The following distribution gives the dialy income of 50 workers of a factory.

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:
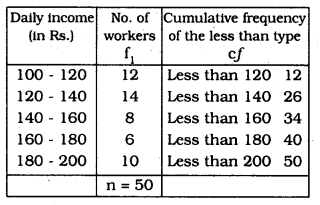
n = 50, ∴ \(\frac{n}{2}\) = 25
On a graph paper mark the following points :
(120, 12), (140, 26), (160, 34), (180, 40), (200, 50).
For the Ogive graph,
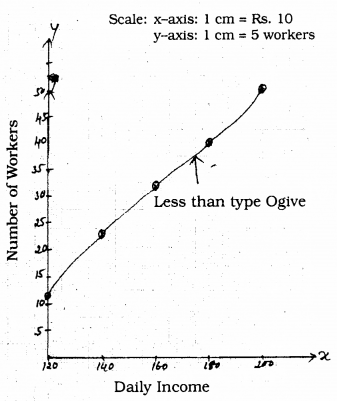
Question 2.
During the medical check-up of 35 students of a class, their weights were recorded as follows :
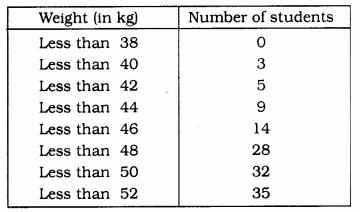
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:
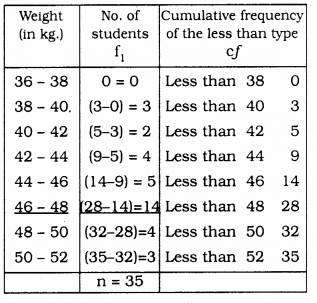
To draw ogive of the less than type.
we have to join the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35).
From the graph, Median is 46.5 kg
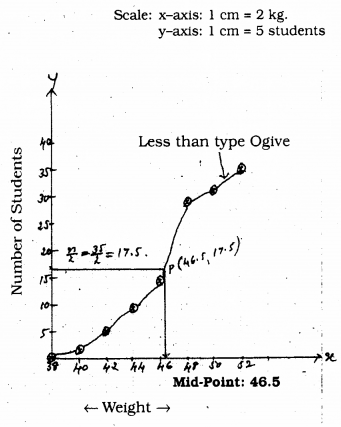
n = 35 ∴ \(\frac{\mathrm{n}}{2}\) = 17.5
Class interval which has median is = (46 – 48)
l = 46, n = 35, f = 14, cf = 14, h = 2
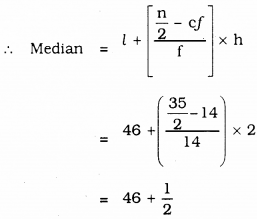
= 46.5
∴ Median = 46.5 kg.
Question 3.
The following table gives production yield per hectare of wheat of 100 farms of a village.
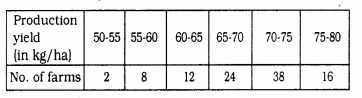
Change the distribution to a more than type distribution, and draw its ogive.
Solution:

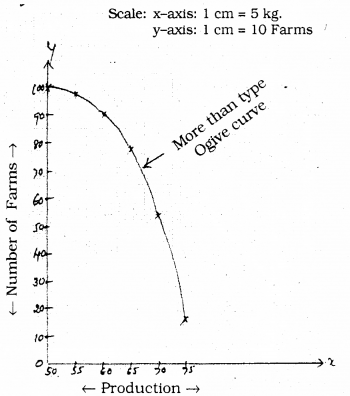
We can draw Ogive graph by plotting ordered pairs:
(50, 100), (55, 98), (60, 90), (65, 78). (70, 54), (75, 16).
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 13 Statistics Ex 13.4 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 13 Statistics Exercise 13.4, drop a comment below and we will get back to you at the earliest.