Students can Download Chapter 7 Congruence of Triangles Ex 7.2, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.2
Question 1.
Which congruence criterion do you use in the following ?
a) Given : AC = D
AB = DE
BC = EF
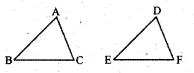
So, ∆ ABC = ∆ DEF
SSS congruence criterion
b) Given : ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆ PQR ≅ ∆ XYZ
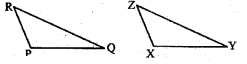
SAS congruence criterion
![]()
c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ∆LMN ≅ ∆GFH
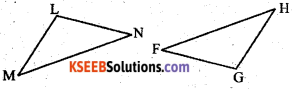
ASA congruence criterion.
d) Given : EB = DB
AE = BC
∠A = ∠C = 90°
So, ∆ ABC ≅ ∆ CDB
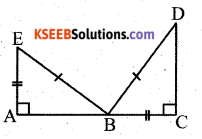
RHS congruence criterion
Question 2.
You want to show that ∆ ART ≅ ∆ PEN,
a) If you have to use SSS criterion, then you need to show
i) AR =
AR = PE,
ii) RT =
RT = EN,
iii) AT =
AT = PN
b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
i) RT =
RT = EN and
ii) PN =
PN = AT
c) If it is given that AT = PN and you to use ASA criterion, you need to have
i) ?
∠ATR = ∠PNE and
ii) ?
∠TAR = NPE.
Question 3.
You have to show that ∆ AMP ≅ ∆ AMQ.
In the following proof, supply the missing reasons
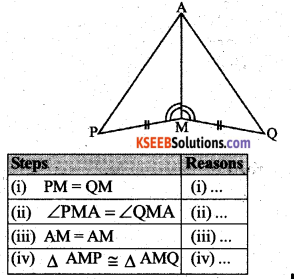

Question 4.
In ∆ ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ∆ PQR,
![]()
A student says that ∆ ABC ≅ ∆ PQR by AAA congruence criterion. Is he justified? Why or why not?
Solution:
No, he is not justified because AAA is not a criterion for the congruence of triangles.
Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆ RAT ≅ ?
Solution:
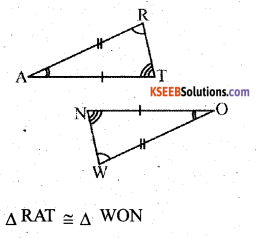
Question 6.
Complete the congruence statement:
Solution:
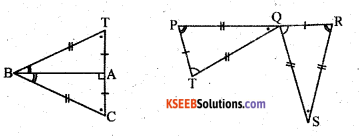
∆ BCA ≅ ? ∆ QRS ≅ ?
∆ BCA ≅ ? ∆ BTA ≅ ?
∆ QRS ≅ ? ∆ TPQ
![]()
Question 7.
In a squared sheet, draw two triangles of equal areas such that
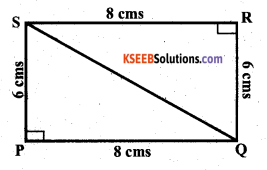
i) The triangles are congruent.
Solution:
Consider the ∆S PQS and SQR
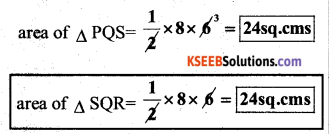
In ∆ PQS and ∆ SQR
PS = QR = 6 cms
∠SPQ = ∠QRS = 90°
QS = QS = common
By RHS congruence criterion
∆PQS ≅ ∆SQR.
Perimeter of the ∆ PQS = PQ + QS + PS
Perimeter of the ∆ SQR = SR + QS + QR
∴ Perimeter of the ∆ PQS = Perimeter of the ∆ SQR (∵ PQ = SR & PS = QR)
ii) the triangles are not congruent. What can you say about their perimeters?
Solution:
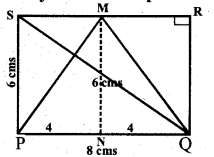

∴ area of ∆ PQS = Area of ∆ PQM.
By seeing the figure the ∆ PQS = PQ + PS + SQ = 8 + 6 + 10 = 24 cms.
Perimeter of the ∆ PQM = PQ + PM + QM
= 8 + 7.2 + 7.2
= 22.4 cms.
∴ Their perimeters are not equal.
PM = QM
(PM)2 = PN2 + MN2
= 42 + 62
= 16 + 36 = 52
PM = QM = \(\sqrt{52}\) = 7.2
Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Solution:
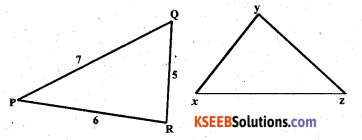
Considering the two triangles PQR and XYZ
In ∆ PQR and XYZ
PQ = XZ = 7 cms
PR = YZ = 6 cms
RQ = XY = 5 cms
∠PRQ = ∠XYZ
∠PQR = ∠XZY
In the above 2 triangles 5 pairs of the congruent present. Still, they are not congruent.
Question 9.
If ∆ ABC and ∆ PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
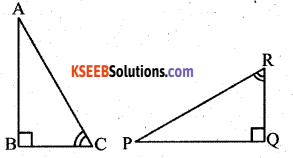
The additional corresponding part is BC = RQ by ASA congruence rules
![]()
Question 10.
Explain, why ∆ ABC ≅ ∆ FED
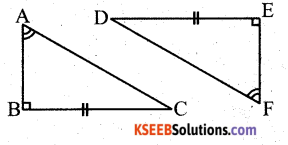
Solution:
∠ABC = ∠DEF = 90°
BC = DE ∠ACD = ∠EDF
( ∵ The sum of the measures of three angles of a triangle is 180°.)
∴ ∆ ABC ≅ ∆ DEF
(By ASA congruence criterion.)