Students can Download Chapter 6 The Triangles and Its Properties Ex 6.4, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.4
Question 1.
Is it possible to have a triangle with the following sides ?
i) 2 cm, 3 cm, 5 cm.
Solution:
greatest side is 5 cms.
2 + 3 = 5
Here sum of the side is equal to third side.
So it is impossible to construct the triangle by given measures.
Because the property of a triangle says that the sum of the two sides of a triangle is greater than the length of the third side.
ii) 3 cm, 5 cm, 7 cm
Solution:
The greatest side is 7 cm.
3 + 6 = 9 cms > 7
6 + 7 = 13 > 3
7 + 3 = 10 > 6
∴ It is possible to construct the triangle with the sides of 3, 6 and 7 cms.
![]()
iii) 6 cm, 3 cm, 2 cm
6 + 3 = 9 > 2
3 + 2 = 5 > 6
2 + 6 = 8 > 3
∴ It is not possible to construct the triangle with the sides of 6, 3 and 2 cms.
Question 2.
Take any point ‘O’ in the interior of a triangle PQR. Is
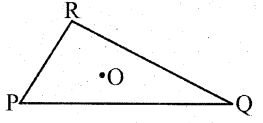
i) OP + OQ > PQ
Solution:
Yes. Sum of the length of any two sides of a triangle is greater than the length of the 3 side.
ii) OQ + OR > QR
Solution:
Yes, Sum of the length of any two sides of a triangle is greater than the length of the 3rd side.
iii) OR + OP > RP
Solution:
Yes, Sum of the length of any two sides of a triangle is greater than the length of the 3rd side.
![]()
Question 3.
AM is a median of a triangle ABC. Is AB + BC + CA > 2 AM ?
(Consider the sides of triangles ∆ ABM and ∆ AMC.)
Solution:
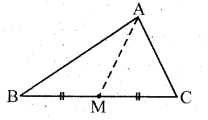
Consider the triangle ABM
In ∆ ABM
AB + BM > AM — 1 (Sum of the length of any 2 sides of a triangle is greater that the 3rd side.)
In ∆ ACM
CM + CA > AM — 2 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
Add 1 and 2
(AB + BM) + (CM + CA) > AM + AM
AB + (BM + CM) + CA > 2AM
AB + BC + CA > 2AM (yes, it is proved.)
Question 4.
ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?
Solution:
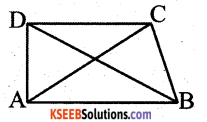
Consider the ∆ ABC
AB + BC > CA — 1 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
In ∆ ACD
AD + CD > AC — 2 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
Adding 1 and 2
AB + BC + CD + DA > 2AC — 3
In ∆ ABD
AB + DA > BD — 4 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
In ∆ BCD
BC + CD > BD — 5 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
Adding 4 and 5
AB + DA + BC + CD > 2BD — 6
Adding 3 and 6
![]()
∴ AB + BC + CD + DA > AC + BD (yes, it is proved)
![]()
Question 5.
ABCD is quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD) ?
Solution:
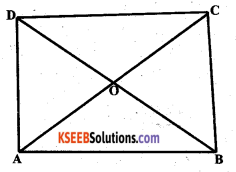
In ∆ AOB OA + OB > AB — 1 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
In ∆ BOC
OB + OC > BC — 2 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
In ∆ COD
OC + CD > CD — 3 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
In ∆ AOD
OA + OD > AD — 4 (Sum of the length of any 2 sides of a triangle is greater than the 3rd side.)
Add all the 4

∴ AB + BC + CD + DA< 2 (AC + BD) (proved)
Question 6.
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution:
Let ‘x’ cm to the length of the 3rd side.
According to the sum of the length of any 2 sides of a triangle is greater than 3rd side.
∴ 12 + 15 >x
27 > x
or x < 27 15 + x > 12
x > 12 – 15 = -3
x + 12 > 15
x > 15 – 12 = 3
∴ x > -3 and x > 3 we should take x > 3
∴ The length of 3rd side of a triangle should be in between 3 cm and 27 cms.