Students can Download Class 10 Maths Chapter 5 Areas Related to Circles Additional Questions Questions, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your in examinations
Karnataka State Syllabus Class 10 Maths Chapter 5 Areas Related to Circles Additional Questions
I. Multiple Choice Questions:
Question 1.
The radius of a circle is 5cm, then its area is
a) 154 cm3
b) 1386 cm3
c) 169 cm3
d) 308 cm3
Answer:
a) 154 cm3
Question 2.
The diameter of a semicircle is 4cm Its area is.
a) π cm2
b) 2π cm2
c) 4π cm2
d) 8π cm2
Answer:
b) 2π cm2
Question 3.
The radii of two concentric circles are 3cm and 2cm. the ratio of their areas.
a) 3 : 4
b) 9 : 2
c) 9 : 4
d) 4 : 3
Answer:
c) 9 : 4
Question 4.
The diameter of a circle whose area is equal to the areas of two circles of radii 24cm and 7cm is
a) 25 cm
b) 31 cm
c) 28 cm
d) 50 cm
Answer:
d) 50 cm
Question 5.
The radius of a circle is 21cm then its circumference is
a) 66 cm
b) 33 cm
c) 132 cm
d) 99 cm
Answer:
c) 132 cm
Question 6.
Formula to find area of Quadrant is
a) \(\frac{\pi r^{2}}{2}\)
b) πr2
c) \(\frac{\pi r^{2}}{3}\)
d) \(\frac{\pi r^{2}}{4}\)
Answer:
d) \(\frac{\pi r^{2}}{4}\)
Question 7.
Find the perimeter of a Quadrant of a circle of radius 7cm.
a) 25 cm
b) 49 cm
c) 14 cm
d) 66 cm.
Answer:
a) 25 cm
Question 8.
If the perimeter and the area of a circle are equal numerically, then the diameter of the circle is.
a) 8 units.
b) n units
c) 4 units
d) 2 units.
Answer:
c) 4 units
Question 9.
The central angle of a Quadrant of a circle measures.
a) 60°
b) 90°
c) 120
d) 30°
Answer:
b) 90°
Question 10.
The measure of the central angle of a circle is.
a) 360°
b) 180°
c) 270°
d) 90°
Answer:
a) 360°
Question 11.
If the diameter of a semi-circular protractor is 7cm, then its perimeter is
a) 7 cm
b) 36 cm
c) 21 cm
d) 18 cm
Answer:
d) 18 cm
Question 12.
The external and internal radius of a circular path are 5m and 3m respectively. The area of the circular path is.
a) 87π m2
b) 167π m2
c) 157π m2
d) 327π m2
Answer:
b) 167π m2
Question 13.
Find the area of a ring-shaped region enclosed between two concentric circles of diameter 8cm and 6cm.
a) 22 cm2
b) 44 cm2
c) 66 cm2
d) 88 cm2
Answer:
a) 22 cm2
![]()
Question 14.
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is.
a) 11 : 4
b) 22 : 7
c) 14 : 1
d) 7 : 22
Answer:
c) 14 : 1
Question 15.
The area of circle whose circumference is 44cm is
a) 77 cm2
b) 308 cm2
c) 168 cm2
d) 154 cm2
Answer:
d) 154 cm2
Question 16.
A bicycle wheel makes 2500 revolutions in moving. 11km. Find the circumference of the wheel.
a) 220 cm
b) 55 cm
c) 110 cm
b) 100 cm.
Answer:
c) 110 cm
Question 17.
The minute hand of a clock is of length 4cm. then the angle swept by the minute hand in 15 minutes.
a) 45°
b) 60°
c) 120
d) 90°
Answer:
d) 90°
Question 18.
The perimeter of the sector with radius 10.5cm and sector angle 60° is
a) 23 cm
b) 32 cm
c) 35 cm
d) 28 cm
Answer:
b) 32 cm
Question 19.
The radius of a semicircular protractor is 35m. then its perimeter.
a) 90 m
b) 45 m
c) 180 m
d) I20 m.
Answer:
c) 180 m
Question 20.
The area swept out by a horse tied in a rectangular grass field with a rope 8m long is
a) 647π m2
b) 327π m2
c) 128π m2
a) 48π m2
Answer:
a) 647π m2
Question 21.
The area (in cm2) of the circle that can be inscribed in a square of side 8cm is.
a) 64π
b) 16π
c) 8π
d) 32π
Answer:
b) 16π
Question 22.
The area of a circle that can be inscribed in a square, of side 10cm is
a) 407π cm2
b) 307π cm2
c) 1007π cm2
d) 257π cm2
Answer:
d) 257π cm2
Question 23.
The area of the largest triangle that can be inscribed in a semicircle of radius r is
a) r2
b) 2r2
c) r2
d) 2r3
Answer:
a) r2
Question 24.
The area of the largest square that can be inscribed in a circle of radius 12cm is.
a) 24 cm2
b) 249 cm2
c) 288 cm2
d) 196 \(\sqrt{2}\) cm2
Answer:
c) 288 cm2
Question 25.
The perimeter of a square circumscribing a circle of radius a unit is
a) 2a units
b) 4a units
c) 8a units
d) 16a units.
Answer:
c) 8 a units
![]()
II. Short Answer Questions:
Question 1.
Find the area of the circle inscribed in a square of side b cm.
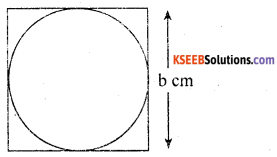
Answer:
Diameter of a circle = b ; r = b/2
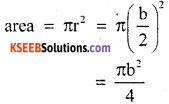
Question 2.
Find the area of a square inscribed in a circle of radius a.
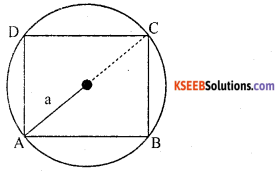
Answer:
radius = a & diameter = 2a
Diagonal of square = 2a
AC2 = AB2 + BC2
(2a)2 = (side)2 + (side)2
4a2 = 2side2
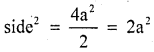
Area of square = side2 = 2a2.
Question 3.
If the diameter of semicircular protractor is 14 cm then find its perimeter.
Answer:
Perimeter of semicircular protractor
= πr + diameter
= \(\frac{22}{7}\) × 7 + 14 = 22 + 14 = 36 cm.
Question 4.
Find the number of revolutions if circumference of a wheel is 22cm and travells a distance 110km.
Answer:
Number of revolutions

Question 5.
If circumference and the area of a circle are numerically equal, find the diameter of the circle
Answer:
2πr = πr2
2r = r2
r = 2
d = 2r = 2 × 2 = 4 units.
Question 6.
Difference between the circumference and radius of a circle is 37cm. Find the area of circle.
Answer:
2πr – r = 37
r(2π – 1) = 37
pppppppp
Question 7.
Find the radius the area of a circular playground is 22176m2
Answer:
Area of circular playground = 22176 m2
πr2 = 22176
\(\frac{22}{7}\) r2 = 22176
r = 84 m
![]()
III. Long Answer Questions.
Question 1.
The area of a circular playground is 2217m2. Find the cost of fencing this ground at the rate of? 50 per/m.
Answer:
Area of circular playground

= 44 x 12
= 528 m
Cost of fencing this ground
= 528 x 50
= ₹ 26400
Question 2.
The circumference of a circle exceeds the diameter by 16.8cm. Find the radius of the circle.
Answer:
Let the radius of circle be r cm.
∴ Diameter = 2r cm
circumference = 2πr cm
circumference = 16.8 + Diameter
2πr = 16.8 + 2r

Hence radius is 3.92 cm
Question 3.
A race track is in the form of a ring whose inner circumference is 352m, and the outer circumference is 396 in. Find the width of the track.
Answer:
Inner circumference = 352m
27πr = 352m

∴ Width of track = R – r = 63 – 56 = 9m
Question 4.
The minute hand of a clock is 10cm long. Find the area of the face of the clock described by the minute hand between 10 AM and 10-30 AM.
Answer:
Angle described by the minute hand in one minute = 6°
∴ Angle describes by minute hand between 10 AM and 10.30 Am = 30 minutes = 30 x 6 = 180°
∴ Area swept by the minute hand in 30 minutes
= Area of sector of circle radius 10cm

Question 5.
A circle of radius 6cm is inscribed in a square as shown in the given figure. Find the shaded region.
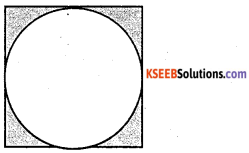
Answer:
From the figure, side of a square = Diameter of a circle = 2r
= 2 x 6 = 12cm
∴ Area of square = (side)2
= (12)2 = 144cm2
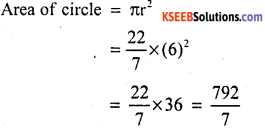
∴ Area of the shaded region
= Area of square-Area of the circle
= 144 – 133.04
= 30.96 cm2
![]()
Question 6.
Find the length of the arc that subtends an angle of 72° at the centre of a circle of radius 5cm.
Answer:

Question 7.
In the given figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10cm as centers, to intersect the sides BC, CA and AB at their respective midpoints D,E and F. Find the area of the shaded region.
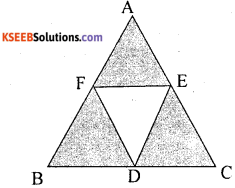
Answer:
= \(\frac{1}{2}\) (Side of equilateral ∆le)
= \(\frac{1}{2}\) × 10 = 5 cm
Area of shaded region
= Sum of areas of there equal sectors

Question 8.
A paper is in the form of a rectangle ABCD in which AB = 18 cm and BC = 14cm. A semicircle with BC as diameter is cut off. Find the area of the remaining portion.
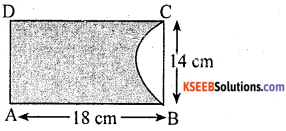
Answer:
∴ Area of rectangle ABCD = l × b
= AB × BC
= 18 × 14 = 252 cm2
Radius of semicircle (r)
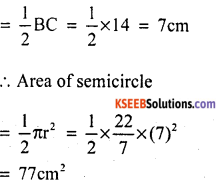
Area of the remaining portion
= 252 – 77
= 175cm2
![]()