Students can Download Class 10 Maths Chapter 1 Arithmetic Progressions Additional Questions, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your in examinations
Karnataka State Syllabus Class 10 Maths Chapter 1 Arithmetic Progressions Additional Questions
I. Multiple-choice Questions:
Question 1.
If an = n2 – 1 and an = 99 then the value of n is
a) 100
b) 10
c) 9
d) 99
Answer:
b) 10
Question 2.
If an= 2n2 – 1 then the value of 4th term is
a) 32
b) 30
c) 31
d) 18
Answer:
c) 31
Question 3.
If an= 2n + 1 then the common difference of the AP is
a) 3
b) 5
c) 2
d) 1
Answer:
c) 2
Question 4.
The general form of an A.P is
a) a, ar, ar2,…
b) a, a + d, a + 2d,…
c) a, a-d,.a-2d,….
d) \(\frac{1}{a}, \frac{1}{a+d}, \frac{1}{a+2 d}\) …..
Answer:
b) a, a + d, a + 2d,…
Question 5.
In an A.P the common difference is 3 first term is 1 then the value of 10th term is
a) 28
b) 27
c) 25
d) 40
Answer:
a) 28
Question 6.
The formula to find nth term of an A.P is.
a) a + (n – 1)d
b) arn-1
c) \(\frac{1}{a+(n-1) d}\)
d) a – (n + 1)d
Answer:
a) a + (n – 1)d
Question 7.
If 20, x + 1, 4 are In AP then value of x is
a) 11
b) 12
e) 24
d) 13
Answer:
a) 11
Question 8.
In an arithmetic progression an+5 = 35 & an+1 = 23 then common difference is
a) 3n
b) 4n
c) 2
d) 3
Answer:
d) 3
![]()
Question 9.
In an A.P the relation between a5 and a7 and common difference is (d) is
a) a5 = a7 + 2d
b) a5 = a7 + d
c) a7 = a5 + 3d
d) a7 = a5 + 2d
Answer:
d) a7 = a5 + 2d
Question 10.
If a is constant then a + 2a + 3a +…. + na is

Answer:
![]()
Question 11.
The value of Σ(n – 1) s
a) \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\)
b) \(\frac{n(n-1)}{2}\)
c) \(\frac{n}{2}\)
d) \(\frac{n^{2}}{2}\)
Answer:
b) \(\frac{n(n-1)}{2}\)
Question 12.
In an A.P, if S5 = 35 and S4 = 22 then 5th term is.
a) 35
b) 10
c) 13
d) 22
Answer:
c) 13
Question 13.
The nth term of 3, 7, 11, 15, is
a) 4n – 1
b) 4n + 1
c) 4n + 3
d) 3n + 4
Answer:
a) 4n – 1
Question 14.
In an A.P, if a4 = 8 & a = 2, then its common difference is
a) 6
b) 4
c) 2
d) 10
Answer:
c) 2
Question 15.
In an A.P an+5 = 50 and an+1 = 38 then common difference
a) 3
b) 2
c) 3n
d) 2n
Answer:
a) 3
Question 16.
Among the following arithmetic progression is
a) 1, 4, 6,…
b) 12, 10, 14,…
c) 35, 32, 25,….
d) 8, 13, 19,
Answer:
c) 35, 32, 25,….
Question 17.
In an AP, the correct relation is
a) an-5 = an-4 + d
b) an-5 = an-6 + d
C) an-5 = an + d
d) an+5 = an-5 – d
Answer:
b) an-5 = an-6 + d
Question 18.
The value of \(\sum_{n=1}^{n}10\) is
a) 10
b) 11
c) 55
d) 110
Answer:
c) 55
Question 19.
If 2x + 1, 4x, 13-x are in Arithmetic progression then x is equal to
a) 2
b) 3
c) 4
d) 5
Answer:
a) 2
Question 20.
In a progression, if an = 2n2 + 1, then S2 is
a) 9
b) 12
c) 10
d) 11
Answer:
b) 12
II. Short answer Questions:
Question 1.
Write the formula to find nth term of an A.P?
Answer:
an = a + (n – 1)d
Question 2.
Write the formula to find arithmetic mean of 3 numbers
Answer:
AM = \(\frac{a+b+c}{3}\)
Question 3.
The first term of an A.P is q and its common difference is p. Find its 20th term.
Answer:
a20 = a + 19d
= q + 19p
![]()
Question 4.
If an = 5n – 3, find the common difference
Answer:
an = 5n – 3
a1 = 5(1) – 3 = 5 – 3 = 2
a2 = 5(2) – 3 = 10 – 3 = 7
d = a2 – a1 = 7 – 2 = 5
common difference = 5
Question 5.
Find the 9th term from the end (towards the first term) of the A.P 5, 9, 13, ….185
Answer:
a = 185, d = – 4 & 1 = 5
a9 = a + (n – 1)d
a9= 1 + (9 – 1) – 4
a9 = 185 + 8x – 4
= 185 – 32
a9 = 153
Question 6.
For what value of p are 2p + 1, 13, 5p – 3, three consecutive terms of a AP?
Answer:
a2 – a1, = a3 – a2
13 – (2p + 1) = 5p – 3 – 13
13 – 2p – 1 = 5p – 16
12 + 16 = 5p + 2p
7p = 28

p = 4
Question 7.
Find the common difference of an AP in which a18 – a14 = 32
Answer:
a18 – a14 = 32
(a + 17d) – (a + 13d) = 32
a + 17d – a – 13d = 32
4d = 32

d = 8
Question 8.
In an A.P an = 20 & Sn = 399 find Sn-1
Answer:
an = Sn – Sn-1
Sn-1 = Sn – an
= 399 – 20
Sn-1 = 379
Question 9.
In an AP, if d = – 4, n = 7, an = 4 then find a.
Answer:
an = a + (n – 1)d
4 = a + (7 – 1) – 4
4 = a + 6 x – 4
4 = a – 24
a = 4 + 24
a = 28
III. Long Answer Questions:
Question 1.
Find the number of terms in the A.P, 100, 96, 92,….., 12
Answer:
100, 96, 92,………, 12
a = 100 d = a2 – a1, d = 96 – 100 = – 4
an = 12 & n = ?
an = a + (n – 1)d
12 = 100 + (n – 1)d
12 – 100 = (n – 1) x – 4
– 88 = (n – 1) x – 4
\(\frac{-88}{-4}\) = n – 1
n – 1 = 22
n = 22 + 1
n = 23
Question 2.
The angles of a triangle are in A.P if the smallest angle is 50°, find the other two angles.
Answer:
Let the smallest angle = 50°
Three angles of AP are a, a + d, a + 2d – Sum of the angles of a triangle = 180° a + a + d + a + 2d = 180°
50° + 50° + d + 50° + 2d = 180°
3d = 180°- 150°
3d = 30°

d = 10°
Required angles a = 50°
a + d = 50° + 10° = 60°
a + 2d = 50 + 2(10) = 50 + 20 = 70°
Question 3.
An A.P consists of 50 terms of which 3rd term is 12 and last term is 106. Find the 29th term.
Answer:
n = 50
a3 = 12
a + 2d = 12
a = 12 – 12d → (1)
a = 106
a29 = ?
an = a + (n – 1) d
106 = 12 – 2d + (50 – 1)d
106 – 12 = – 2d + 49d
94 = 47d

d = 2
Put d = 2 is eqn (1)
a = 12 – 2 (2)
a = 12 – 4
a = 8
![]()
Question 4.
The sum of 4th and 8th terms of an A.P is 24 and the sum of 6th and 10th terms of the same A.P is 44. Find the first three terms.
Answer:
Sum of 4th and 8th terms = 24
a4 + a8 = 24
a + 3d + a + 7d = 24
2a + 10d = 24
÷ by 2 on both the sides
a + 5d = 12 → (1)
Sum of 6th and 10th terms = 44
a6 + a10 = 44
a + 5d + a + 9d = 44
2a + 14d = 44 by 2
a + 7d = 22 → (2)
Subtract eqn (1) & (2)
a + 5d = 12
a + 7d = 22
(-) (-) (-)
________
– 2d = – 10
+ d = \(\frac{10}{2}\) = 5
Put d = 5 is eqn (1)
a = 12 – 5d
a = 12 – 5(5)
= 12 – 25 a = – 13
required terms a, a + d, a + 2d…….
– 13, – 13,+ 5, – 13 + 2(5)
– 13,- 8, – 3
Question 5.
The ratio of 7th to 3rd term of an A.P is 12 : 5 find the ratio of 13th to 4th term
Answer:
\(\frac{a_{7}}{a_{3}}=\frac{12}{5}\)
\(\frac{a+6 d}{a+2 d}=\frac{12}{5}\)
5(a + 6d) = 12 (a + 2d)
5a + 30d= 12a + 24d
30d – 24d = 12a – 5a
6d = 7a
d = \(\frac{7}{6}\) a
The ratio of 13th to 4th term

Question 6.
A company employed 400 persons in the year 2001 and each year increased by 35 persons. In which year the number of employees in the company will be 785?
Answer:
2001 + 2002 ………………..
400, 435, 470, ………….. 785
a = 400, d = a2 – a1 an = 785, n = ? d = 435 – 400
d = 35
an = a + (n – 1)d
785 = 400 + (n – 1) 35
785 – 400 = (n – 1) × 35
385 = (n – 1) x 35
n – 1 = \(\frac{385}{35}\)
n – 1 = 11
n = 11 + 1
n = 12
Employes in the company will be 785 reach in year 2012.
Question 7.
If the pth term of an A.P is q and the qth term is p. Prove that the nth term equal to (p + q – n)
Answer:
Let a be the first term and ‘d’ the common difference
ap = a + (p – 1)d and aq = a + (q – 1)d
Now ap = q and aq = p given
a + (p – 1)d = q → (1)
a + (q – 1)d = p → (2)
On subtracting (1) from (2) we get

Putting d = – 1 in the eqn (i) we get a + (p – 1 ) x – 1 = q
a – p + 1 = q a = p + q – 1
∴ nth term = a + (n – 1)d
= p + q – 1 + (n – 1) x – 1
= p + q – 1 + n + 1
nth term = p + q – n
Hence it is proved
Question 8.
Find four numbers in A.P such that the sum of 2nd and 3rd terms is 22 and the product of 1st and 4th terms is 85.
Answer:
Sum of 2nd and 3rd terms = 22

Question 9.
Find the sum of all natural numbers between 1 and 201 which are divisible by 5.
Answer:
5 + 10 +15 +………….+ 200
which are divisible by 5
a = 5
d = a2 – a1 = 10 – 5 = 5
l = an = 200 + (n – 1)d
200 = 5 + (n – 1) x 5
195 = (n – 1) x 5
n – 1 = \(\frac{195}{5}\)

Question 10.
Find three numbers in AP whose sum and products are respectively. 21 and 231
Answer:
Let the numbers be a – d, a, a + d
Sum = 21
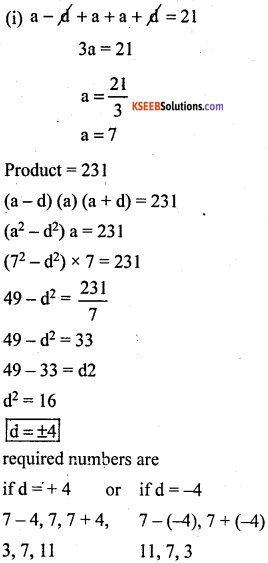
Question 11.
The sum of 6 terms which form an A.P is 345. The difference b/w the first and last terms is 55 find the terms.
Answer:
Let the numbers be a, a + d, a + 2d, a + 3d
a + 4d, a + 5d, a + 6d
6d + 15d = 345 – 3
2a + 5d = 115 → (1)
the difference b/w first term and last term is 55
a6 – a1 = 55
a + 5d – a = 55
5d = 5
d = \(\frac{55}{5}\)
d = 11
Put d = 11 in eqn (1)
2a + 5d = 115
2a + 55 = 115
2a = 115 – 55
2a = 60
a = \(\frac{60}{2}\)
a = 30
required numbers
a, a + d, a + 2d, a + 3d, a + 4d, a + 5d
30, 30 + 11, 30 + 2(11), 30 + 3(11), 30 + 4(11), 30 + 5(11)
30, 41, 52, 63, 74, 85.
![]()
Question 12.
In an AP whose first term is 2, the sum of first five terms is one fourth the sum of the next five terms show that T20 = – 112, Find S20.
Answer:
Let the five number a, a + d, a + 2d, a + 3d, a + 4d, next 5 numbers be
a + 5d, a + 6d, a + 7d, a + 8d, a + 9d a = 2
a + a + d + a + 2d + a + 3d + a + 4d
= \(\frac{1}{4}\) (a + 5d + a + 6d + a + 7d + a + 8d + a + 9d)
5a + 10d = \(\frac{1}{4}\) (5a + 35d)
5(2) + 10d = \(\frac{1}{4}\) [(5 x 2) + 35d]
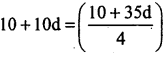
4(10 + 10d) = 10 + 35d
40 + 40d = 10 + 35d
40d – 35d = 10 – 40
5d = – 30
d = \(\frac{-30}{5}\)
d = – 6
a20 = ?, n = 20
an = a + (n – 1)d
a20 = 2 + (20 – 1) x 6
= 2 – 114 a20 = – 112
a20 = l = – 112
S20 = ? n = 20
S = f{2+(-112)]
s20 =10(2-112) = 10(-110)
s20 = -1100
Question 13.
The third term of an A.P is 8 and the ninth term of the A.P exceeds three times the third term by 2 find the sum of its first 19 terms.
Answer:
a3 = 8 (given)
a + 2d = 8 → (1)
a9 = 3(a3) + 2 (given)
a + 8d = 3(8) + 2 [bye qn (1)]
a + 8d = 26
a + 2d + 6d = 26
8 + 6d = 26 (a + 2d = 28)
6d = 26 – 8
6d = 18
d = \(\frac{18}{6}\)
d = 3
Put d = 3 in eqn (1)
a + 2(3) = 8
a + 6 = 8
a = 8 – 6
a = 2
n = 19
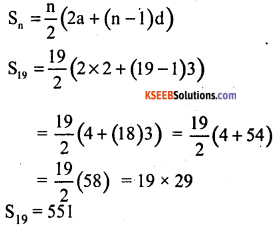
Question 14.
If the sum of m terms of an AP is the same as the sum of its n terms, show that the sum of its (m + n) terms is 120°. Find the number of sides of the zero.
Answer:
Let a be the first term and d be the common difference of the given AP
Then Sm = Sn
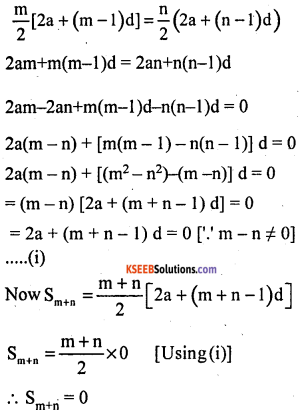
Question 15.
Find the sum of all the first ‘n’ odd natural numbers.
Answer:
1, 3, 5, 7, 9,…… up to n
a = 1, d = 3 – 1 = 2, n = n

Question 16.
The common difference between any two consecutive Interior angles of a polygon is 5°. If the smallest angle is 120°. Find the number of sides of the polygon?
Answer:
Let the AP be 120°, 125°…… with
a = 120°and d = 5
The number of sides in a polygon is the sum of its interior angles. Therefore (2n – 4)90°
= 180n – 360°
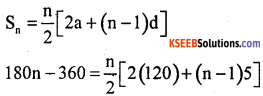
2 [180n- 360] = n [240 + 5n – 5]
360n – 720 = n (235 + 5n)
360n – 720 = 235n + 5n2
5n2 + 235n – 360n + 720 = 0
5n2 – 125n + 720 = 0 + by 5
n2-25n + 144 = 0
n2 – 16n – 9n + 144 0
n(n – 16) – 9(n – 16) = 0
(n – 16) (n – 9) = 0
n – 16 = 0, and n – 9 = 0
n = 16 and n = 9
∴ n = 9
∴ number of sides is 9 so it is a nanogon.
Question 17.
In an AP whose first term is 2, the sum of first five terms is one fourth the sum of the next five terms show that T20 = – 112
Answer:
a = 2, S5 =\(\frac{1}{4}\)[S10 – S5], T20 = – 112
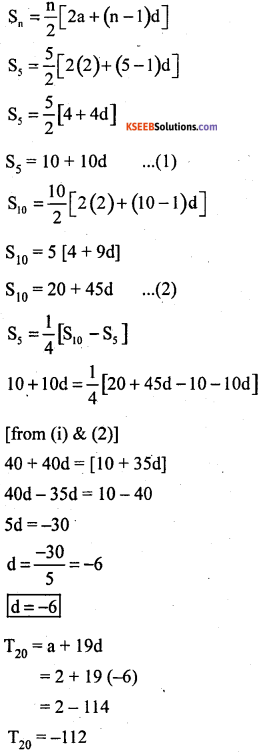
Question 18.
In an arithmetic progression the sum of first 10 terms is 175 and the sum of the next 10 terms is 475 find the arithmetic progression.
Answer:
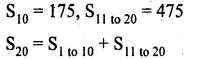


![]()