KSEEB Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.4 are part of KSEEB Solutions for Class 9 Maths. Here we have given Karnataka Board Class 9 Maths Chapter 5 Triangles Exercise 5.4.
Karnataka Board Class 9 Maths Chapter 5 Triangles Ex 5.4
Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.
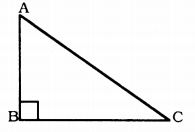
Solution:
In ∆ABC, ∠ABC = 90°
∠A + ∠C = 90°
∠ABC > ∠BAC and ∠ABC < ∠BCA
∴ D is the largest side of ∠ABC.
∴ AC is opposite side of larger angle.
∴ AC hypoternuse is largest side of ∆ABC.
Question 2.
In sides AB and AC of ∆ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
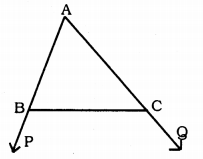
Solution:
Data: AB and AC are the sides of ∆ABC and AB and AC are produced to P and Q respectively.
∠PBC < ∠QCB.
To Prove: AC > AB
Proof: ∠PBC < ∠QCB
Now, ∠PBC + ∠ABC = 180°
∠ABC = 180 – ∠PBC ………. (i)
Similarly, ∠QCB + ∠ACB = 180°
∠ACB = 180 – ∠QCB …………. (ii)
But, ∠PBC < ∠QCB (Data)
∴ ∠ABC > ∠ACB Comparing (i) and (ii), AC > AB
(∵ Angle opposite to larger side is larger)
Question 3.
In fig ∠B < ∠A and ∠C < ∠D. Show that AD < BC.
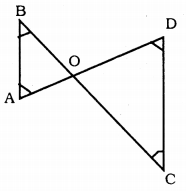
Solution:
Data : ∠B < ∠A and ∠C < ∠D.
To Prove: AD < BC
Proof: ∠B < ∠A
∴ OA < OB …………. (i)
Similarly, ∠C < ∠D
∴ OD < OC …………. (ii)
Adding (i) and (ii), we have
OA + OD < OB + OC
∴ AD < BC.
Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD. Show that ∠A > ∠C and ∠B > ∠D.
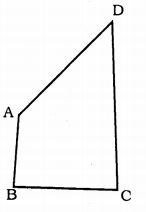
Solution:
Data : AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD.
To Prove :
(i) ∠A > ∠C
(ii) ∠B > ∠D
Construction: Join AC and BD
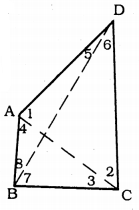
Proof: In ∆ABC, AB < BC (data)
∴ ∠3 < ∠4 ………. (i)
In ∆ADC, AD < CD (data)
∴ ∠2 <∠1 …………. (ii)
Adding (i) and (ii),
∠3 + ∠2 < ∠4 + ∠1
∠C < ∠A
∠A > ∠C
By adding B,
In ∆ABD, AB < AD
∠5 < ∠8
In ∆BCD, BC < CD
∠6 < ∠7
∴ ∠5 + ∠6 < ∠8 + ∠7
∠D < ∠B
OR ∠B > ∠D.
Question 5.
In Fig. PR > PQ and PS bisect ∠QPR. Prove that ∠PSR > ∠PSQ.
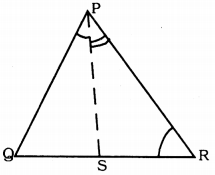
Solution:
Data: PR > PQ and PS bisect ∠QPR.
To Prove: ∠PSR > ∠PSQ
Proof: In ∆PQR, PR > PQ
∴ ∠PQR > ∠PRQ ………. (i)
PS bisects ∠QPR.
∴ ∠QPS = ∠RPS ………… (ii)
By adding (i) and (ii),
∠PQR + ∠QPS > ∠PRQ + ∠RPS ………. (iii)
But, in ∆PQS, ∠PSR is an exterior angle.
∴ ∠PSR = ∠PQR + ∠QPS ………… (iv)
Similarly, in ∆PRS, ∠PSQ is the exterior angle.
∴ ∠PSQ = ∠PRS + ∠RPS ……… (v)
In (iii), subtracting (iv) and (v),
∠PSR > ∠PSQ.
Question 6.
Show that of all line segments drawn from a given point, not on it, the perpendicular line segment is the shortest.
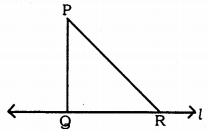
Solution:
P is a point on straight line l.
PR is the segment for l drawn such that PQ ⊥ l.
Now, in ∆PQR,
∠PQR = 90° (Construction)
∴ ∠QPR + ∠QRP = 90°
∴ ∠QRP < ∠PQR
∴ PQ < PR
Any line segment is drawn from P to l they form a small angle.
∴ PQ ⊥ l is smaller.
We hope the KSEEB Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.4 help you. If you have any query regarding Karnataka Board Class 9 Maths Chapter 5 Triangles Exercise 5.4, drop a comment below and we will get back to you at the earliest.