Students can Download 2nd PUC Physics Previous Year Question Paper March 2020, Karnataka 2nd PUC Physics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Physics Previous Year Question Paper March 2020
Time: 3 Hrs 15 Min
Max. Marks: 70
Instructions:
- All parts are compulsory.
- Answer without relevant diagram/figure/circuit wherever necessary will not carry any marks.
- Numerical problems solved without writing the relevant formulae carry no marks.
Part – A
I. Answer ALL the following questions: (10 × 1 = 10)
Question 1.
Write the SI unit of electric flux.
Answer:
Vm.
Question 2.
Graphically represent the variation of resistivity of a semiconductor with absolute temperature.
Answer:

![]()
Question 3.
Give any one use of electromagnet.
Answer:
Electromagnets are used in calling bells, electromagnetic cranes to displace huge or iron material.
Question 4.
What is the significance of Lenz’s law?
Answer:
Lenz’s law is used to find polarity induced emf.
Question 5.
How does capacitive reactance vary with frequency?
Answer:
Xc ∝ \(\frac{1}{2 \pi f}\), Xc ∝ \(\frac{1}{f}\).
Question 6.
Arrange the following electromagnetic waves in ascending order of their wavelength. Radio waves, Gamma rays, Infrared waves, X-rays.
Answer:
Gamma rays, X-rays, Infrared waves, Radio waves.
Question 7.
Why does the sky appear blue?
Answer:
The sky appears blue because of scattering of light by atmospheric particles.
Question 8.
Mention a method to increase the resolving power of a microscope.
Answer:
R.P. = \(\frac{2 n \sin \theta}{\lambda}\)
∴ R.P can be increased by placing a medium of refractive index ‘n’ between the object and the objective.
Question 9.
Write the nuclear reaction equation for alpha decay of ![]()
Answer:
![]()
![]()
Question 10.
Draw the logic symbol of NOR gate.
Answer:
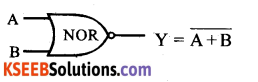
Part – B
II. Answer any FIVE of the following questions: (5 × 2 = 10)
Question 11.
State and explain Coulomb’s law in electrostatics.
Answer:
Coulomb’s law:
‘The Electrostatic force of attraction or repulsion between two stationary point charges separated in free space or air is directly proportional to the product of magnitudes of charge on them and inversely proportional to the square of the distance between them and the force acts along the line joining the two point charges’.
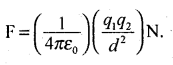

Question 12.
A parallel plate capacitor with air between the plates has capacitance C. What will be the capacitance if
- The distance between the plates is doubled?
- The space between the plates is filled with a substance of dielectric constant 5?
Answer:
- Since C ∝ \(\frac{1}{d}\), capacitance gets halved.
- Since C ∝ ∈r , capacitance increases 5 times.
Question 13.
Write two limitations of Ohm’s law.
Answer:
- Ohm’s law cannot be applied for non-ohmic devices such as semiconductors, electrolytes of a cell, discharge tubes, thermionic valve devices.
- Ohm’s law cannot be applied for conductors for varying temperatures, for temperatures near absolute temperature and for higher temperatures.
![]()
Question 14.
In a region, an electric field \(\overline{\mathbf{E}}\) = 5 × 103 \(\hat{\mathbf{j}}\) NC-1 and a magnetic field of \(\overline{\mathbf{B}}\) = 0.1 \(\hat{\mathbf{k}}\) T are applied. A beam of charged particles are projected along X-direction. Find the velocity of charged particles which move undeflected in this crossed fields.
Answer:

Question 15.
Define ‘retentivity’ and ‘coercivity’.
Answer:
1. Retentivity:
The property of a material to retain the magnetism even after the removal of the magnetising field is known as retentivity.
2. Coercivity:
Coercivity refers to the property of a material which shows the tendency of opposition to the removal of residual magnetism in the material.
Question 16.
Mention two sources of energy loss in transformer.
Answer:
Sources of energy loss in transformers are due to
- Copper loss
- Magnetic flux linkage loss
- Hysteresis loss
- Eddy current loss.
Question 17.
What is displacement current? Give the expression for it.
Answer:
The current in a capacitor is called displacement current.

Question 18.
An alpha particle, a proton and an electron are moving with equal kinetic energy. Which one of these particles has the longest de Broglie wavelength? Give reason.
Answer:
For same K.E., λ ∝ \(\frac{1}{\sqrt{\mathrm{m}}}\)
∵ mα > mp > me; λe > λp > λα
Hence electrons have longest wavelength.
Part – C
III. Answer any FIVE of the following questions: (5 × 3 = 15)
Question 19.
Establish the relation between electric field and electric potential.
Answer:
Consider a point charge ‘+q’. Let ‘P’ be a point initially at infinity. Let ‘A’ be a point inside the . field region. Let ‘+1C’ be a unit positive charge moved from the point at infinity to point ‘A’. Let ‘A’ be at a distance of ‘r’ from the given point charge. Let ‘B’ be another point at distance of ‘dr’, from’A’towards the point charge +q.

The work done in moving positive test charge from Ato B, against the force of repulsion is dW = -Fdr. The -ve sign indicates that the work is done against the direction of the force and dr is the displacement of +1C of test charge in the direction opposite to the electric field.
But electric potential dV = \(\frac{d W}{+q_{0}}\) and electric field
E = \(\frac{\mathrm{F}}{+q_{0}}\)
When q0 = +1C then dW = dV, E = F
Hence dV = -Edr or E = \(-\frac{d \mathrm{V}}{d r}\)
i.e., Electric field intensity at a point is the negative potential gradient at that point and electric field intensity is in the direction of decreasing electrostatic potential.
![]()
Question 20.
Derive the expression for the energy stored in a charged capacitor?
Answer:
Let ‘C’ be the capacitance of a parallel plate capacitor. By definition C = \(\frac{Q}{V}\). By definition amount of work done to raise the charge by ‘dq’ is dW = Vdq.
i.e., dW= \(\frac{q}{C}\)dq
where ‘q’ is the instantaneous value of charge on the conductor.
Total work done in charging the capacitor is given by,

or W = \(\frac{1}{2} \frac{Q^{2}}{C}\), amount of work done is stored in the form of energy.
Therefore E = \(\frac{1}{2}\left(\frac{Q^{2}}{C}\right)\)
Using Q = CV, E = \(\frac{1}{2}\)CV2, where ‘ V is the maximum voltage supplied to a capacitor.
Question 21.
Give the principle of cyclotron and draw the neat labelled schematic diagram of cyclotron.
Question 22.
Mention three properties of diamagnetic materials.
Question 23.
Arrive at the relation between focal length and radius of curvature of a spherical concave mirror.
Answer:
- The distance between the pole and the principle focus of the mirror is called focal length (f).
- f = \(\frac{\mathrm{R}}{2}\) where R – radius of curvature of a spherical mirror.
Question 24.
Using Huygen’s principle, show that the angle of incidence is equal to the angle of reflection when a plane wavefront is reflected by a plane surface.
Question 25.
Define work function. Write Einstein’s photoelectric equation and explain the terms.
Answer:
Work function:
The minimum energy which is just enough to liberate electrons from a given surface is called its photo electric work function.
hv = w + \(\frac{1}{2}\)mv2, E = hv
energy of incidence photon.
Where W – work function; \(\frac{1}{2}\) mv2 = maximum kinetic energy of photo electrons
![]()
Question 26.
Give three differences between intrinsic and extrinsic semiconductors.
Answer:
| Intrinsic Semiconductors | Extrinsic Semiconductors |
| 1. These are semiconductors without doping. | These are semiconductors with doping. |
| 2. Number density of electrons = Number density of holes | Number density of electrons ≠ Number density of holes. |
| 3. Resistivity is large | Resistivity is less than those of intrinsic semiconductors. |
Part – D
IV. Answer any TWO of the following questions: (2 × 5 = 10)
Question 27.
Derive the expression for conductivity of a material: σ = \(\frac{\mathbf{n} \mathrm{e}^{2} \tau}{\mathbf{m}}\); where the terms have their usual meaning.
Question 28.
Obtain the expression for the force between two straight long parallel conductors carrying current. Hence define ‘ampere’.
Answer:
X and Y are two long straight parallel conductors carrying currents I1 and I2 respectively, and placed close to each other. d is the separation between the two conductors and L is the length of the conductors.
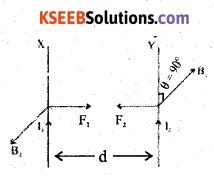
The magnetic field at any point on the conductor Y due to current I1 in the conductor X, is given by
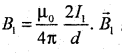
Acts in a direction perpendicular to the plane containing the two conductors. The conductor Y which carries current I2, experiences a mechanical force due to B1 acting on it and this force is given by F1 = B1 I2 L sin θ.
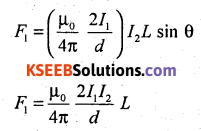
According to Fleming’s left hand rule, the direction of the force F1 on X is perpendicular to B2 and is towards the conductor Y.
The magnetic field at any point on the conductor X due to the current I2 in y, is given by
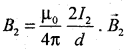
Acts on X and opposite to B1. The mechanical force acts on X due to B2 is I1 L sin θ.
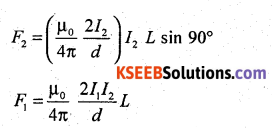
According to Fleming’s left hand side rule, the direction of the force F2 on X is perpendicular to X and it is towards the conductor y if the current I1 is inwards (or away from the conductor Y if the current I2 is outwards).
The Force F1 acting on a certain length of the conductor Y due to the current in the conductor X is equal in magnitude to the force F2 acting on the same length of X due to the current in conductor Y.
If the two conductors carry the currents in the same direction (parallel currents) then the forces attract each other. If the two conductors carry the currents in the opposite directions (anti parallel currents), then they are found to repel each other because the two forces act away from each other.
The force per unit length on each conductor is
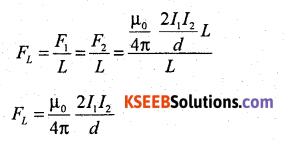
One ampere of current can be defined as that constant current which when maintained through each of the two infinitely long straight parallel conductors of negligible area of cross section in the same direction placed 1 metre apart in vacuum, causes an attractive force of 2 × 10-7 N m-1 length on each conductor.
![]()
Question 29.
With the help of a labelled diagram, derive the expression for instantaneous emf induced in an AC generator.
V. Answer any Two of the following questions: (2 × 5 = 10)
Question 30.
Obtain the expression for the fringe width of interference fringes in Young’s Double slit experiment.
Answer:
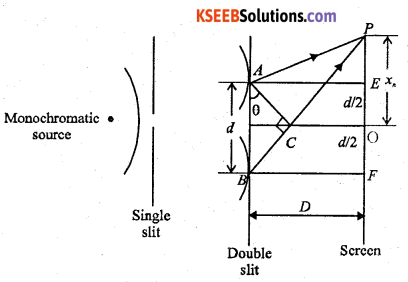
Let A and B be two slits separated by a distance ‘d’. Let ‘λ’ be the wavelength of light. Let ‘D’ be the distance between the screen and the double slit.
Let ‘C’ be a point on BP such that AP ≈ CP.
Path difference between the two waves reaching ‘P’ is given by BP – AP = BC = δ.
From the Δ BFP, BP2 = BF2 + FP2 and from the Δ AEP, AP2 = AE2 + EP2
BP2 – AP2 = (D2 + FP2) – (D2 – EP2)
i.e; BP2 – AP2 = FP2 – EP2
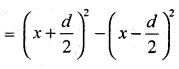
(BP – AP) (BP + AP) = 2(2x.\(\frac{d}{2}\))
For a point ‘p’ close to ‘O’,
BP ≈ AP = D
(BP – AP) (2D) = 2x.d.
But (BP – AP) = BC = δ
i.e; δ = \(\frac{x d}{D}\)
or
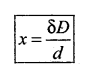
For a constructive interference δ = nλ.
![]()
Distance of nth bright fringe from the central bright fringe xn = n\(\frac{\lambda D}{d}\)
Distance of (n + 1)th bright fringe from the central bright fringe xn+1 = (n + 1)\(\frac{\lambda D}{d}\)
By definition, Fringe width is the distance between two consecutive bright or dark fringes.
xn+1 – xn = β = \(\frac{\lambda}{d}\)(n + 1 – n)
i.e;
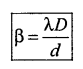
Fringe width β ∝ D, β ∝ λ and β ∝ \(\frac{1}{d}\).
We can show that the fringe width between any two dark fringes is also β = \(\frac{\lambda D}{d}\).
Question 31.
Using Bohr’s postulates, derive the expression for the radius of nth stationary orbit of electron in hydrogen atom. Hence write the expression for Bohr radius.
Answer:
Consider an atom of atomic number Z. The charge on its nucleus is + Ze. Let an electron of mass m and charge ‘-e’ revolve round the nucleus in a circular orbit.
Let v be its velocity.
The coulomb’s electrostatic force of attraction between the electron and the nucleus is
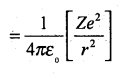
This provides the centripetal force \(\frac{m v^{2}}{r}\) needed for the orbital motion of the electron.

From Bohr’s Quantization rule, for the nth orbit,
we have, mvr = \(\frac{n h}{2 \pi}\) _______(2)
Squaring equation (2)
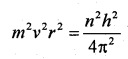 ______(3)
______(3)
Dividing equation (3) by equation (1)

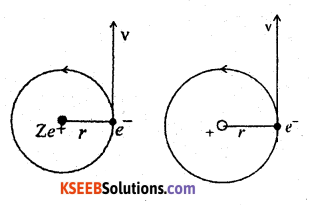
For H2 atom put Z = 1 and r = \(\frac{\varepsilon_{0} n^{2} h^{2}}{\pi m e^{2}}\). For I orbit, put n = 1
i.e; r = ε0h2/ πme2 for the I orbit of hydrogen atom.
![]()
Question 32.
What is rectification? Explain the working of a p-n junction diode as a half wave rectifier. Draw the input and output waveforms.
Answer:
The process of conversion of ac into pulsating dc is called rectification.
Answer:
The circuit of a half wave rectifier using a semiconductor diode is shown in figure below.
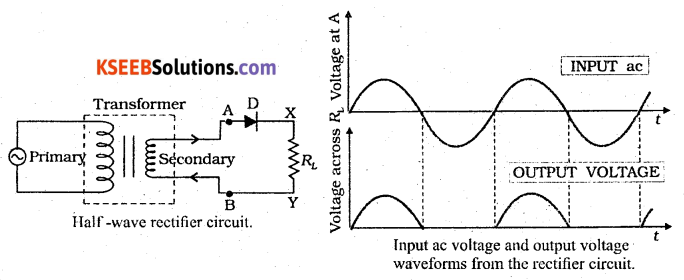
The diode in series with a load resistor is connected to the secondary of a transformer. The AC voltage to be rectified is applied to the primary of the transformer.
This produces induced voltage across the secondary of the transformer. During the positive half cycles of transformer output i.e., when A is positive, diode D is forward biased and hence it conducts. During negative half cycles, the diode D is reverse biased and hence does not conduct. Current flows through the diode circuit only during positive half cycles. The current flowing through load resistance RL produces the rectified voltage.
VI. Answer any THREE of the following questions: (3 × 5 = 15)
Question 33.
Two point charges qA = 5μC and qB = -5μC are located at A and B separated by 0.2 m in vacuum.
- What is the electric field at the midpoint O of the line joining the charges?
- If a negative test charge of magnitude 2nC is placed at O, what is the force experienced by the test charge.
Answer:
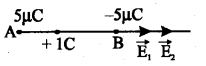
We know that: Electric field at a point due to a point charge

Net electric field at P = E1 + E2
= 2 × 4.5 × 106 Vm-1 along AB.
i.e. E = 9.0 × 106 Vm-1 along AB.
Force on q0 = -2nC is given by
F = Eq0 = – 9 × 106 × 2 × 10-9 = – 1.8 × 10-2 N along BA.
![]()
Question 34.
- Three resistors 3Ω, 4Ω and 12Ω are connected in parallel. What is the effective resistance of the combination.
- If the combination is connected to a battery of emf 6V and internal resistance 0.5Ω, find the current drawn from the battery and terminal potential difference across the battery.
Answer:
1. We know that \(\frac{1}{\mathrm{R}_{\mathrm{p}}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}}\)

2. We know I =

and V = IR = 3 × 1.5 = 4.5 V
Question 35.
A series LCR circuit contains a pure inductor of inductance 5.0H, a capacitor of capacitance 20pF and a resistor of resistance 40Ω.
- Find the resonant frequency of the circuit.
- Calculate the quality factor (Q-factor) of the circuit.
- What is the impedance at resonant condition?
Solution:
Given L = 5H, C = 20 × 10-6 F, R = 40Ω, f0 = ?, Q = ?
1. We know that f0 =
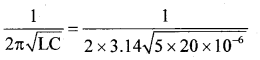
2. ∴ f0 = 15.92Hz
3.

Impedance of the circuit at resonance = Z = R = 40Ω.
![]()
Question 36.
At what angle should a ray of light be incident on the face of an equilateral prism, so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.5
Answer:
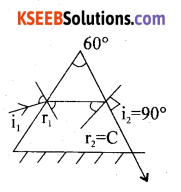
Given A = 60°, i2 = 90°, n = 1.5
r2 = C, i1 = ?
We know that n = \(\frac{1}{\sin C}\)
i.e. sinC = \(\frac{1}{1.5}=\frac{2}{3}\) = 0.6667
hence C = 41.8°.
For non-syittmetric refraction A = r1 + r2
i.e. r1 = A – r2 = 60° – 41.8°= 18.2°
since n = \(\frac{\sin \mathrm{i}_{1}}{\sin \mathrm{r}_{1}}\)
sin i1 = 1.5 × sin 18.2° = 1.5 × 0.3123
i.e. sin i1 = 0.4685
or
![]()
Angle of incidence = 27.9°.
![]()
Question 37.
A copper coin has a mass of 63.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. The coin is entirely made of 2963Cu atoms.
Mass of 2963Cu atom = 62.92960 u
Mass of proton = 1.00727 u
Mass of neutron = 1.00866 u
Avogadro’s number = 6.022 × 1023.
Answer:
rest mass of constituents:
rest mass of 29 protons =29 × 1.00727 = 29.21083 u
rest mass of 34 neutrons =34 × 1.00866 = 34.29444 u
rest mass of 29 electrons = 29 × 0.00055 = 0.01595 u
63.52122 u
Mass defect Δm = rest mass of constituents – rest mass of atom
i.e. Δm = 63.52122 – 62.92960 = 0.59162 u
Energy equivalent of mass defect
B.E. = 0.59162 × 931 MeV = 550.79822 MeV per atom
i.e. E = (550.79822 × 106 × 1.6 × 10-19) × (6.023 × 1023) J.
i.e. E = 5.307 × 1013 J is required to separate all the nucleous in 63.0 g of copper coin.