Students can Download Maths Chapter 4 Determinants Ex 4.4 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 4 Determinants Ex 4.4
2nd PUC Maths Determinants NCERT Text Book Questions and Answers Ex 4.4
Write the minors and co-factors of the elements of following determinants
Question 1.
(i)
\(\left|\begin{array}{cc}{2} & {-4} \\{0} & {3}\end{array}\right|\)
Answer:

(ii)
\(\left|\begin{array}{ll}{a} & {c} \\{b} & {d}\end{array}\right|\)
Answer:
![]()
![]()
![]()
Question 2
(i)
\(\left|\begin{array}{lll}{\mathbf{1}} & {\mathbf{0}} & {\mathbf{0}} \\{\mathbf{0}} & {\mathbf{1}} & {\mathbf{0}} \\{\mathbf{0}} & {\mathbf{0}} & {\mathbf{1}}\end{array}\right|\)
Answer:
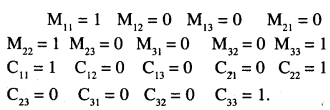
(ii)
\(\left|\begin{array}{ccc}{1} & {0} & {4} \\{3} & {5} & {-1} \\{0} & {1} & {2}\end{array}\right|\)
Answer:

Question 3.
Using cofactors of elements of second row, Evaluate
\(\Delta\left|\begin{array}{lll}{1} & {0} & {0} \\{0} & {1} & {0} \\{0} & {0} & {1}\end{array}\right|\)
Answer:
C21 = 0 C22 = 1 C23 = 0
∴ Δ A = 0 x 0 + 1 x 1 + 0 x 0 = 1
![]()
Question 4.
Using cofactors of elements of 3rd column
\(\Delta=\left|\begin{array}{lll}{\mathbf{1}} & {\mathbf{x}} & {\mathbf{y} \mathbf{z}} \\{\mathbf{1}} & {\mathbf{y}} & {\mathbf{z} \mathbf{x}} \\{\mathbf{1}} & {\mathbf{z}} & {\mathbf{x} \mathbf{y}}\end{array}\right|\)
Answer:
M13 = (z – y) M23 = (z-x) M33 = (y-x)
C13 = (z-y) C23 = -(z-n), C33 = (y – x)
Δ = yz (z – y) + zx{-(z – x)} + xy (y – x)
= yz2 – y2z – z2x + zx2 + xy2 – x2y
x2 (z – y) + z (y2 – z2) + yz (z – y)
x2 (z – y) + x (y+ z) (y- z) + yz (z – y)
(z – y) {x2 – x (y + z) + yz}
(z – y) {x2 – xy – xz + yz}
(z – y) {x (x – y) – z (x – y)}
(z – y) (x – y) (x – z) = (z – y) (y – x) (z – x)
![]()
Question 5.
\(\text { If } \Delta=\left|\begin{array}{lll}{\mathbf{a}_{11}} & {\mathbf{a}_{12}} & {\mathbf{a}_{13}} \\{\mathbf{a}_{21}} & {\mathbf{a}_{22}} & {\mathbf{a}_{23}} \\{\mathbf{a}_{31}} & {\mathbf{a}_{32}} & {\mathbf{a}_{33}}\end{array}\right|\) is a cofactors of aij then the calue of Δ is given by of
(A) a11 A31 + a12 A32 + a13 A33
(B) an An + a12 A21 + a13 A31
(C) a21 Au + a22 A12 + a23 A13
(D) an An + a21 A21 + a31 A31
Answer:
Answer is (D)
i.e., a11 A11 + a21+ a31 A31