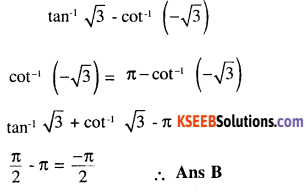Students can Download Maths Chapter 2 Inverse Trigonometric Functions Ex 2.2 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
2nd PUC Maths Question Bank Chapter 2 Inverse Trigonometric Functions Ex 2.2
2nd PUC Maths Inverse Trigonometric Functions NCERT Text Book Questions and Answers Ex 2.2
Question 1.
\(3 \sin ^{-1} x=\sin ^{-1}\left(3 x-4 x^{3}\right), \quad x \in\left[-\frac{1}{2}, \frac{1}{2}\right]\)
Answer:
Let sin-1 x be θ ⇒ x = sin θ
In RHS putting the value of x
sin-1 (3x – 4x3) ⇒ sin-1 (3 sinθ – 4 sin3θ)
= sin-1 (sin 3θ)
[∵ 3sinθ – 4sin3 θ = sin3θ]
= 3θ
putting the value of θ
3θ = 3 sin-1 x = LHS
∴ 3sin-1 x = sin-1 (3x – 4x3)
Hence proved.
![]()
Question 2.
\(3 \cos ^{-1} x=\cos ^{-1}\left(4 x^{3}-3 x\right), x \in\left[\frac{1}{2}, 1\right]\)
Answer:
Let cos-1 x be θ ⇒ x = cos θ
In RHS, putting the value of x
cos-1 (4x3 – 3x) ⇒ cos1 (4cos3 θ – 3 cosθ)
⇒ cos-1 (cos 3θ)
[∵ 4cos3 θ – 3cosθ = cos 3θ]
= 30
putting the value of 0 = 30
⇒ 3 cos-1 x = LHS
LHS = RHS
Hence proved
Question 3.
\(\tan ^{-1} \frac{2}{11}+\tan ^{-1} \frac{7}{24}=\tan ^{-1} \frac{1}{2}\)
Answer:
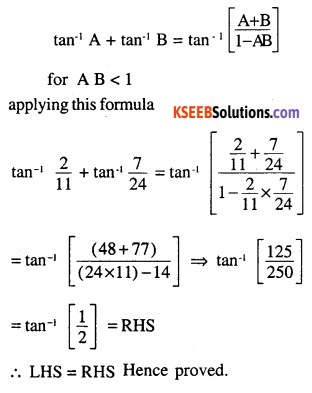
Question 4.
\(2 \tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{7}=\tan ^{-1} \frac{31}{17}\)
Answer:


![]()
Write the following function in the simplest form:
Question 5.
\(\tan ^{-1} \frac{\sqrt{1+x^{2}}-1}{x}, x \neq 0\)
Answer:

Question 6.
\(\tan ^{-1} \frac{1}{\sqrt{x^{2}-1}},|x|>1\)
Answer:
Let cosec-1 x = 0
⇒ x = cosec 0

Question 7.
\(\tan ^{-1}(\sqrt{\frac{1-\cos x}{1+\cos x}}), 0<x<\pi\)
Answer:
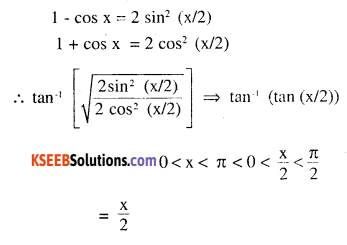
Question 8.
\(\tan ^{-1}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right), \frac{-\pi}{4}<x<\frac{3 \pi}{4}\)
Answer:
Divide each term of numerator and denominator inside the brackets by cos x
\(\Rightarrow \tan ^{-1}\left[\frac{(\cos x-\sin x) / \cos x}{(\cos x+\sin x) / \cos x}\right] \Rightarrow \tan ^{-1}\left[\frac{1-\tan x}{1+\tan x}\right]\)
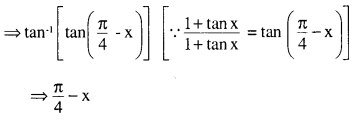
Question 9.
\(\tan ^{ -1 } \frac { { x } }{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } } ,|{ x }|<{ a }\)
Answer:

![]()
Question 10.
\(\tan ^{-1}\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right), a>0 ; \frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\)
Answer:

Find the values of each of the following
Question 11.
\(\tan ^{-1}\left[2 \cos \left(2 \sin ^{-1} \frac{1}{2}\right)\right]\)
Answer:

Question 12.
cot (tan-1 a + cot-1 a)
Answer:

Question 13.
\(\begin{aligned}&\tan \frac{1}{2}\left[\sin ^{-1} \frac{2 x}{1+x^{2}}+\cos ^{-1} \frac{1-y^{2}}{1+y^{2}}\right]\\&|x|<1, y>0 \text { and } x y<1\end{aligned}\)
Answer:

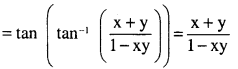
![]()
Question 14.
In \(\sin \left(\sin ^{-1} \frac{1}{5}+\cos ^{-1} x\right)=1\)
Answer:

Question 15.
\(\text { If } \tan ^{-1} \frac{x-1}{x-2}+\tan ^{-1} \frac{x+1}{x+2}=\frac{\pi}{4}\)Then find the value of x
Answer:

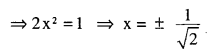
Find the values of each of the expressions in Exercises 16 to 18.
Question 16.
\(\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)\)
Answer:

Question 17.
\( \tan ^{-1}\left(\tan \frac{3 \pi}{4}\right)\)
Answer:
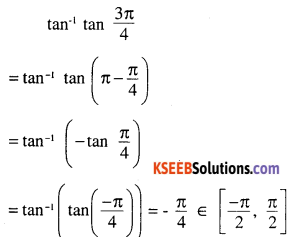
![]()
Question 18.
\(\tan \left(\sin ^{-1} \frac{3}{5}+\cot ^{-1}\left(\frac{3}{2}\right)\right)\)
Answer:
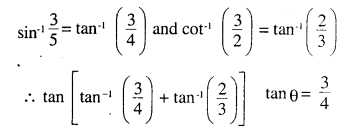

Choose the correct Answer:
Question 19.
\(\cos ^{-1}\left(\cos \frac{7 \pi}{6}\right) \text { is equal to }\)
(A) \(\frac{7 \pi}{6}\)
(B) \(\frac{5 \pi}{6}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{\pi}{6}\)
Answer:

Question 20.
\(\sin \left(\frac{\pi}{3}-\sin ^{-1}\left(-\frac{1}{2}\right)\right)\)is equal to
(A) π
(B) \(-\frac{\pi}{2}\)
(C) 0
(D) \(2 \sqrt{3}\)
Answer:
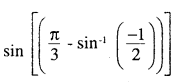

Question 21.
\(\tan ^{-1} \sqrt{3}-\cot ^{-1}(-\sqrt{3})\) is equal to
(A) π
(B) \(-\frac{\pi}{2}\)
(C) 0
(D) \(2 \sqrt{3}\)
Answer: