Students can Download Maths Chapter 12 Linear Programming Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 12 Linear Programming Miscellaneous Exercise
Question 1.
Refer to Example 9. How many packets of each food should be used to maximise the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?
Answer:
| Amount of | P(x) | Q (y) |
| Calcium | 12 | 3 |
| Iron | 4 | 20 |
| Chlosterol | 6 | 4 |
| Vitamin A | 6 | 3 |
Z = 6x + 3y subject to the constraints
(i) 12x + 3y ≥240 ⇒ 4x + y ≥ 80
(ii) 4x + 20y ≥ 460 ⇒x + 5y ≥115
(iii) 6x + 4y ≤ 300 ⇒ 3x + 2y≤150
(iv) x ≥0 ; y≥0
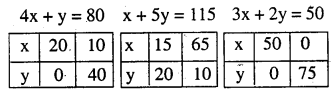
ABC is the solution region
A (15,20) Z = 6 x 15+ 3 x 20= 150
B(40,15) Z = 6 x 40+ 3 x 15 = 285
C (2,72) Z = 6 x 2 + 3 x 72 = 228
Vitamin A is maximised at B (40,15) to 285 if P contains 40 units and Q containts 15 units.
![]()
Question 2.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ? 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ?200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
Answer:

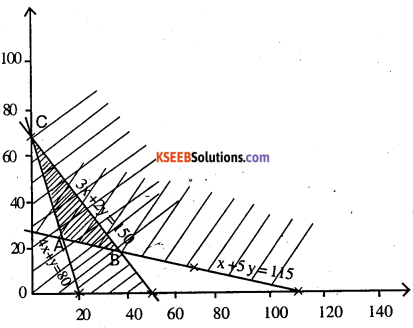
ABCD is the unbounded solution region
A (3,6) Z = ₹ 1950
B (9,2) Z = ₹ 2650
C (0,12) Z = ₹ 2400
D (18,0) Z = ₹ 4500
cost is minimum at A (3,6)
Z = ₹ 1950 with 3 packets of P and 6 packets of Q.
![]()
Question 3.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹ 16 and one kg of food Y costs ₹ 20. Find the least cost of the mixture which will produce the required diet?
Answer:
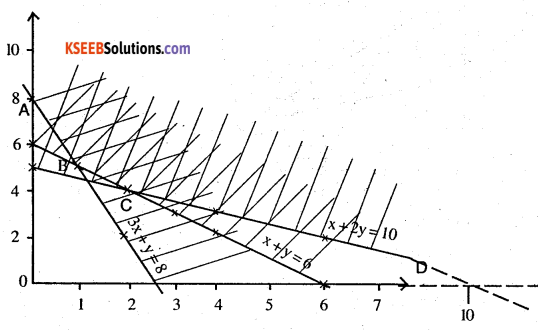
Mininize
Z = 16x +20y Subject to the constraints
(i) x + 2y ≥ 10
(ii) 2x + 2y ≥ 12 ⇒ x + y ≥ 6
(iii) 3x + y ≥ 8
(iv) x ≥ 0; y ≥ 0
shaded region is the un bounded solution region
A (0,8) Z = ₹ 160
B (1,5) Z = ₹ 116
C (2,4) Z = ₹ 112
D (10,0) Z = ₹ 160
The cost is minimised at C (2,4) Z = ₹ 112 2 kg of X and 4 kg of Y.
![]()
Question 4.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | |
| I | II III | |
| A | 12 | 18 6 |
| B | 6 | 0 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is ₹ 7.50 and that on each toy of type B is ₹ 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
Answer:
| Machines | ||||
| Toys | I | II | III | Profit |
| A (x) | 12 | 18 | 6 | ₹ 7.50 |
| B(y) | 6 | 0 | 9 | ₹ 5 |
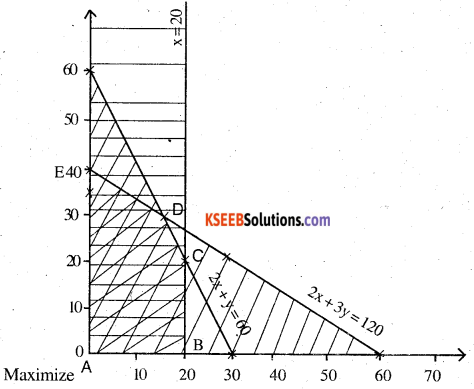
\(Z=\frac{15}{2} x+5 y\) subject to the constraints
(i) 12x + 6y ≤ 360 ⇒ 2x+y ≤ 60
(ii) 18x ≤ 360 ⇒ x ≤ 20
(iii) 6x + 9y ≤ 360 ⇒ 2x +3y ≤ 120
(iv) x ≥ 0 , y ≥ 0
ABCDE is the solution region
A (0, 0) Z = 0
B (20, 0) Z = ₹ 150
C (20, 20) Z = ₹ 250
D (15, 30) Z = ₹ 262.5 ,
E (0, 40) Z = ₹ 200 ‘
At D (15, 30) Z is maximised to ₹ 262. 5
Hence proved.
![]()
Question 5.
An aeroplane can carry a maximum of 200 passengers. A profit of t 1000 is made on-each executive class ticket and a profit of ₹ 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
Answer:
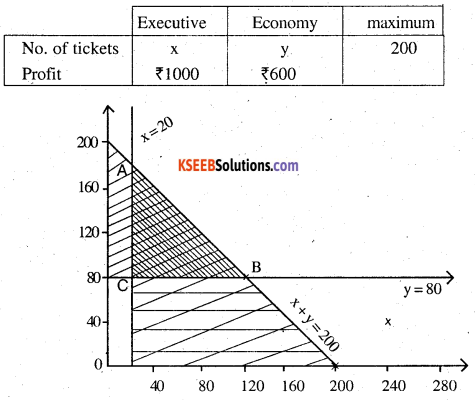
Z = 1000 x + 600 y
subject to the constreint
(i) x + y ≤ 200
(ii) x ≥ 20
(iii) y ≥ 80
(iv) x ≥ 0; y ≥ 0
A (20,180) Z= ₹ 128000
B(120,80) Z= ₹ 168000
C (20,80) Z = ₹ 68000
Z is maximised at B (120, 80) ₹ 168000
120 executive at B 80 economic class tickets
![]()
Question 6.
Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table: How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
| Transportation Cost Per quintal (in ₹) | ||
| From/To | A | B |
| D | 6 | 4 |
| E | 3 | 2 |
| F | 2.50 | 3 |
Answer:
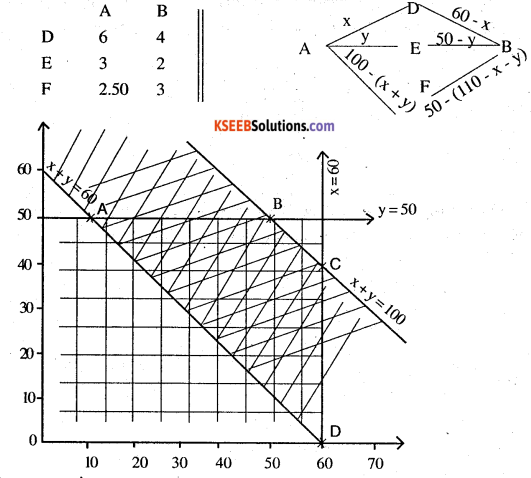

(i) 60 – x ≥ 0 ⇒ x ≤ 60
(ii) 50 – y ≥0 ⇒ y ≤ 50
(iii) 100 – (x + y) ≥ 0 ⇒ x + y ≤ 100
(iv) x + y – 60 ≥ 0 ⇒ x + y ≥ 60
ABCD is the solution region
A (10, 50) Z = ₹ 510
B(50, 50) Z = ₹ 610
C (60, 40) Z = ₹ 620
D (60, 0) Z = ₹ 560
Cost is minimised to ₹ 510 at A (10,50)
Question 7.
An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:
| Distance in (Km) | ||
| From/To | A | B |
| D | 7 | 3 |
| E | 6 | 4 |
| F | 3 | 2 |
Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?
Answer:
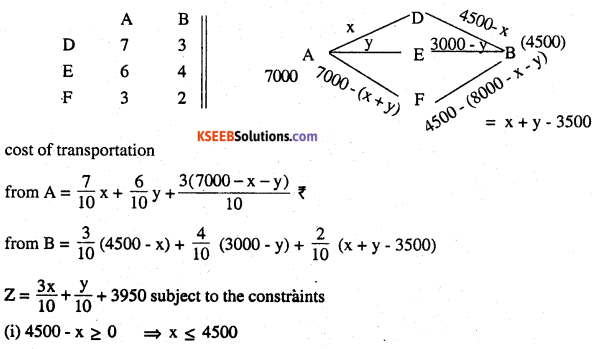
(ii) 3000 – y ≥ 0 = y ≤ 3000
(iii) x + y – 3500 ≥ 0 = x+y ≥ 3500 x ≥ 0
(iv) 7000 – (x + y) ≥ 0= x + y ≥ 3500 y ≥ 0

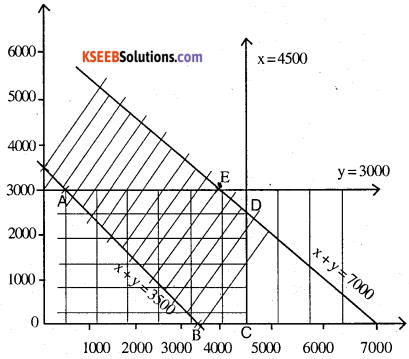
ABCD is the the solution region
A (500, 3000) Z = ₹ 4400
B (3500,0) Z = ₹ 5000
C (4500,0) Z = ₹ 5300
D (4500, 2500) Z = ₹ 5550
E (4000,3000) Z = ₹ 5450
Z is minimised at (500,3000)
i.e. ₹ 4400
From A to D 500 Ltrs
From A to E 3000 Ltrs
From A to F 3500 Ltrs
From B to D 4000 Ltrs.
![]()
Question 8.
A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine. If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
| kg per bag | ||
| Brand P | Brand Q | |
| Nitrogen | 3 | 3.5 |
| Phosphoric acid | 1 | 2 |
| Potash | 3 | 1.5 |
| Chlorine | 1.5 | 2 |
Answer:
| P(x) | Q (y) | |
| N2 | 3 | 3.5 |
| Phosphoric | 1 | 2 |
| Potash | 3 | 1.5 |
| Chlorine | 1.5 | 2 |
\(\text { To minimise } \mathrm{N}_{2} \mathrm{Z}=3 \mathrm{x}+\frac{7}{2} \mathrm{y}\)

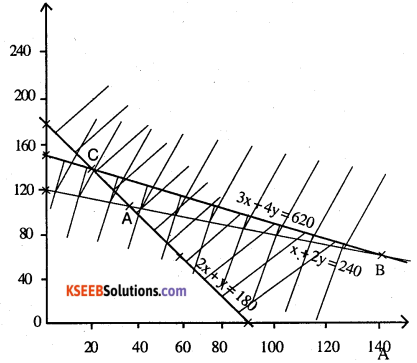
∴ Amount of nitrogen is minimised equal to 470 kg when 40 bags of P and 100 bags of Q are mixed.
![]()
Question 9.
Refer to Question 8. If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?
Answer:
The amount of N2 is maximum equal to 595kg when 140 bags of P and 50 bags of Q are mixed.
Question 10.
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of ₹ 12 and ₹ 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximise the profit?
Answer:
x be the no. of dolls A
y be the no. of dolls B
Maximize Z = 12x + 16 y subject to the constraints
(i) x + y < 1200
(ii) \(y \leq \frac{x}{2} \Rightarrow x-2 y \geq 0\)
(iii) x ≤ 3y + 600 ⇒ x -3y < 600
(iv) x ≥ 0; y ≥0
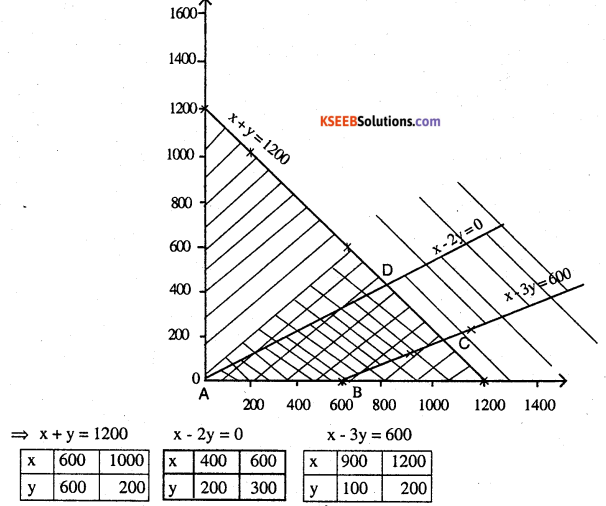
ABCD is the solution region
A (0,0) Z = 0
B (600,0) Z = ₹ 7200
C(1050,150) Z = ₹15000
D (800,400) Z = ₹ 16000
∴ Profit is maximum equal to ₹ 16000 when 800 balls A and 400 balls B are manufactured if sold.
2nd PUC Maths Linear Programming Miscellaneous Exercise Additional Question and Answers
Question 1.
One kind of cake required 300g of flour and 15g of fat, another kind requires 150gm of flour and 30gm of fat. Find the maximum number of cakes which can be made from 7.5kg of flour and 600gm of fat. (CBSE 2010)
Answer:
Let the 1st type of cake x and
2nd type of cake be y
∴ maximize z = x + y subject to
300x + 150 y ≤ 7500, 2x + y ≤ 50
15 x + 30 y ≤ 600 x + 2y ≤ 40
x ≤ 0, y ≤0
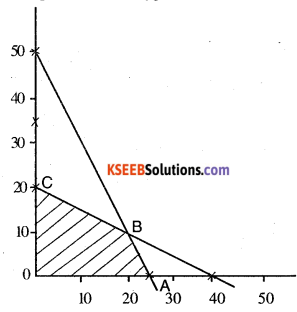
comer point are (0,0), (25,0) (20, 10), (0, 20)
At 0, Z = 0
A, Z = 25
B, Z = 30 – Maximum
C, C = 20
Maximum at B (20, 10)
∴ 20 pieces of 1 st type and
10 pieces of 2nd type cake
![]()
Question 2.
A merchant plans to sell two type of computer and desktop model and a portable model that will cost ₹ 25,000/ and ₹ 40,000. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computer should stock to get maximum profit if he does not want to invest more than 70 lakhs and his profit on the desktop models is ₹ 4500/ and on the portable model is ?5000/ (CBSE 2011)
Answer:
No. of desktop computer be x and no. of portable be y
Maximize
∴ Z = 4500 x + 5000 y
subject to x + y ≤ 250
25000 x + 4000 y ≤ 70,00,000
or 5x + 8y ≤ 1400, x ≥ 0, y
The corner points are.
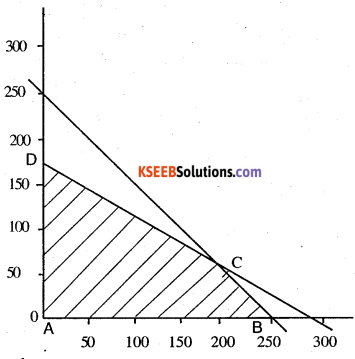
0 (0,0), B (250,0), C (200,50), D (0,175)
At 0, Z = 0
At C Z = 1150000
B Z= 1125000
D Z = 875000
Maximum of C (200, 50)
∴ No. of desktop model = 200
No. of portable = 50