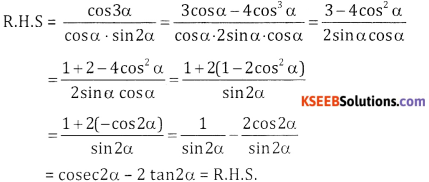2nd PUC Basic Maths Question Bank Chapter 14 Compound Angles, Multiple Angles, Submultiple Angles & Transformation Formulae Ex 14.2

Students can Download Basic Maths Exercise 14.2 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Basic Maths Question Bank Chapter 14 Compound Angles, Multiple Angles, Submultiple Angles & Transformation Formulae Ex 14.2

Part – A & B

2nd PUC Basic Maths Compound Angles, Multiple Angles, Submultiple Angles & Transformation Formulae Ex 14.2 One or Two Marks Questions and Answers

Question 1.
If sin A = \(\frac { 1 }{ 2 }\) find sin 2A
Answer:
Given sin A = \(\frac { 1 }{ 2 }\) ⇒ cos A = \(\frac{\sqrt{3}}{2}\) sin2A

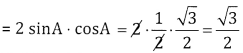
Question 2.
If cos A = \(\frac{\sqrt{3}}{2}\) find cos 2A
Answer:

Question 3.
If tan A = \(\frac{1}{\sqrt{3}}\) find tan 2A
Answer:

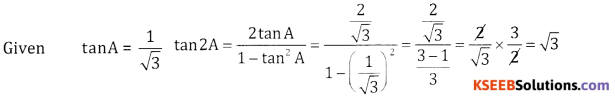
Question 4.
If sin A = \(\frac { 3 }{ 5 }\) find sin 3A
Answer:
Given sin A = \(\frac { 3 }{ 5 }\) sin3A = 3sinA – 4sin³A = \(3 \cdot \frac{3}{5}-4\left(\frac{3}{5}\right)^{3}\)
\(=\frac{9}{5}-4 \cdot \frac{27}{125}=\frac{225-108}{125}=\frac{117}{125}\)

Question 5.
If cos A = \(\frac { 4 }{ 5 }\) 4 find cos 3A
Answer:
Given cos A = \(\frac { 4 }{ 5 }\)

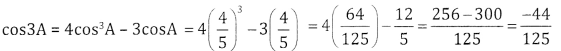
Question 6.
If tan A = \(\frac { 3 }{ 4 }\) find tan 3A
Answer:

Question 7.
Find the value of 3 sin 10° – 4 sin³10°
Answer:
3sin10° – 4sin³10° is of the form 3 sin A – 4sin³A = sin3A = sin 3-10° = sin 30° = \(\frac { 1 }{ 2 }\)

Question 8.
If cot A = \(\frac { 12 }{ 5 }\) and A is acute find sin3A
Answer:
Given cot A = \(\frac { 12 }{ 5 }\) ⇒ sin A = \(\frac { 5 }{ 13 }\) cosA = \(\frac { 12 }{ 13 }\)
∴ sin 3A = 3sinA – 4 sin³A

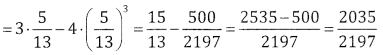
Question 9.
Show that tan A = \(\frac{\tan (A-B)+\tan B}{1-\tan (A-B) \tan B}\)
Answer:

Question 10.
Prove that \(\frac{\cos 2 A}{1+\sin 2 A}=\frac{\cos A-\sin A}{\cos A+\sin A}\)
Answer:

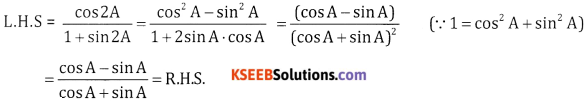
Question 11.
Prove that \(\frac{1+\sin 2 \theta}{\cos 2 \theta}=\frac{1+\tan \theta}{1-\tan \theta}\)
Answer:

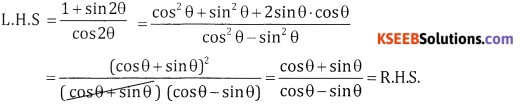
Question 12.
Prove that \(\frac{\sin A+\sin 2 A}{1+\cos A+\cos 2 A}=\tan A\)
Answer:

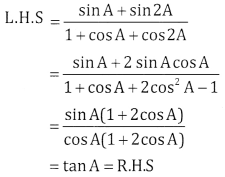
Question 13.
Prove that \(\frac{\sin 2 \theta}{1+\cos 2 \theta}=\tan \theta\)
Answer:

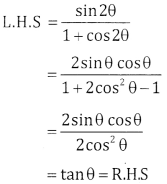
Question 14.
Prove that (sin A – cos A)² = 1 – sin 2A
Answer:
L.H.S (sinA – cosA)²
= sin²A + cos²A – 2sinA cosA
= 1 – sin2A = R.H.S.

Question 15.
Prove that cos⁴θ – sin⁴θ = 2 cos²θ – 1
Answer:
L.H.S. cos⁴θ – sin⁴θ
= (cos²θ)² – (sin²θ)²
= (cos²θ + sin²θ) (cos²θ – sin²θ)
= 1 . (cos²θ – (1 – cos²θ)
= cos²θ – 1 + cos²θ = 2cos²θ – 1 = R.H.S.

Question 16.
Prove that \(\frac{\cos ^{3} A-\sin ^{3} A}{\cos A-\sin A}=1+\frac{1}{2} \sin 2 A\)
Answer:

Part – C

2nd PUC Basic Maths Compound Angles, Multiple Angles, Submultiple Angles & Transformation Formulae Ex 14.2Five Marks Question and Answers

Prove the following

Question 1.
\(\frac{1+\cos 2 A+\sin 2 A}{1-\cos 2 A+\sin 2 A}=\cot A\)
Answer:

Question 2.
\(\frac{\cos 3 A}{2 \cos 2 A-1}=\cos A\) and hence find cos 15°
Answer:

Question 3.
\(\frac{1-\cos 2 A+\sin 2 A}{1+\cos 2 A+\sin 2 A}=\tan A\)
Answer:

Question 4.
cos⁶A+ sin⁶A = 1 – \(\frac { 3 }{ 4 }\) sin³(2A)
Answer:
cos⁶A+ sin⁶A [∵ a³ + b³ = (a + b)³ – 3ab(a+b)]
= (cos²A)³ + (sin²A)³
= (cos²A + sin²A)³ – 3cos²A – sin²A(cos³A + sin³A)
= 1³ – 3cos²A · sin²A.1

Question 5.
Provfe that \(\frac{\sin 3 \theta}{\sin \theta}-\frac{\cos 3 \theta}{\cos \theta}=2\)
Answer:

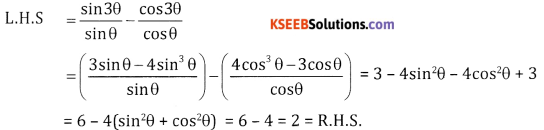
Question 6.
sec (45° + A) · sec(45° – A) = 2 sec 2A
Answer:

Question 7.
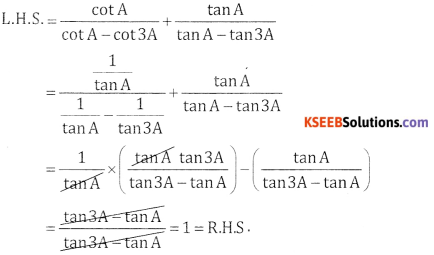
\(\frac{\cot A}{\cot A-\cot 3 A}+\frac{\tan A}{\tan A-\tan 3 A}=1\)
Answer:

Question 8.
Prove that \(\frac{\cos 2 A}{1+\sin 2 A}\) = tan(45° – A)
Answer:

Question 9.
If tan α = \(\frac { 1 }{ 3 }\), tan β = \(\frac { 1 }{ 7 }\) P.T. tan(2α + β) = 45°.
Answer:
L.H.S = tan(2α + β)

tan(2α + β) = 1 = tan 45° = R.H.S.

Question 10.
If tan²(45° + θ) = \(\frac { a }{ b }\) prove that \(\frac{b-a}{b+a}\) = – sin 2θ
Answer:

Question 11.
Prove that tan 2θ – tanθ = tan θ . sec 2θ.
Answer:
L.H.S = tan2θ – tanθ

Question 12.
Prove that cos 2α – tan α = \(\frac{\cos 3 \alpha}{\cos \alpha \cdot \sin 2 \alpha}\)
Answer: