Students can Download 2nd PUC Basic Maths Model Question June 2018 with Answers, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Model Question June 2018 with Answers
Time: 3.15 hours
Max. Marks: 100
Instructions
- The question paper has 5 parts A, B, C, D, and E. Answer all the parts.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C carries, Part – D carries 30 marks and Part – E carries 10 marks.
- Write the question number properly as indicated in the question paper.
Part – A
I. Answer all the questions: (10 × 1 = 10)
Question 1.
If A = \(\left[\begin{array}{ccc}1 & -5 & 4 \\2 & 3 & 6\end{array}\right]\) find 4A’.
Solution:
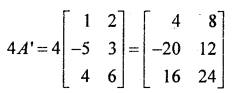
Question 2.
If \(^{n} C_{8}=^{n} C_{5}\), find n.
Solution:
n = 8 + 5 = 13
![]()
Question 3.
Write symbolically “If two numbers are equal then their squares are equal”.
Solution:
p → q
Question 4.
Find third proportional of 7 and 28.
Solution:
7 : 28 : : 28 : x
x = \(\frac { 28\times 28 }{ 7 }\) = 112
![]()
Question 5.
What income can be obtained from ₹ 8,000 of 4% stock?
Solution:
For 100 Rs. → Income 4 Rs.
for 8000 Rs → \(\frac{8000 \times 4}{100}\) = Rs. 320
Question 6.
Write the formulae for learning index.
Solution:
Index of learning = \(\frac{\text { Log (learing ratio) }}{\log 2}\)
Question 7.
Find cos 2A if sin A = \(\frac{1}{2}\)
Solution:
Cos 2A = 1 – 2sin2 A = 1 – 2(\(\frac{1}{4}\)) = \(\frac{1}{2}\)
Question 8.
Evaluate: \(\lim _{x \rightarrow 0} \frac{2}{x} \log (1+x)\)
Solution:
\(2 \lim _{x \rightarrow 0} \frac{\log (1+x)}{x}\) = 2 × 1 = 2.
![]()
Question 9.
If y = sec (sec x) find \(\frac{d y}{d x}\).
Solution:
\(\frac{d y}{d x}\) = sec(sec x) . tan(sec x) = sec x . tan x
Question 10.
Evaluate \(\int\left(x^{a}+e^{x}-\frac{1}{x}\right) d x\)
Solution:
\(\left[\frac{x^{a+1}}{a+1}+e^{x}-\log x\right]+C\)
Part – B
II. Answer any ten questions: (10 × 2 = 20)
Question 11.
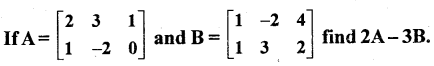
Solution:
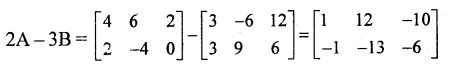
Question 12.
In how many ways can the letters of the word ‘HOPPER’ be arranged?
Solution:
No. of arrangements = \(\frac{6 !}{2 !}\) = 6 × 5 × 4 × 3 = 360
![]()
Question 13.
If P(A) = \(\frac{1}{4}\), P(B) = \(\frac{2}{5}\), P(A∪B) = \(\frac{1}{2}\), find P(A/B).
Solution:

Question 14.
If (~p ∨ q) ∨~r is a false proposition, then find the truth values of p, q and r.
Solution:
F ∨ F = F
~p ∨ q is false
p = T and q = F and r = T
Question 15.
Divide ₹ 6,000 in ratio 3 : 4 : 5.
Solution:
Ist part = \(\frac{3}{12}\) × 6000 = 15000
IInd part = \(\frac{4}{12}\) × 6000 = 2000
IIIrd part = \(\frac{5}{12}\) × 6000 = 2500
Question 16.
T.D on a bill was ₹ 100 and BG was ₹ 10. What is the face value of the bill?
Solution:
Given T.D = 100, B.G = 10, F = ?
BD – TD = BG
⇒ B.D = BG + TD = 100 + 10 = 110
F = \(\frac{B D \times T D}{B . G}\) = \(\frac{110 \times 100}{10}\)
![]()
Question 17.
Prove that (sin A + cos A)2 = 1 + sin 2A.
Solution:
L.H.S = sin2 A + cos2 A + 2 sinA . cosA
= 1 + sin 2A
= R.H.S
Question 18.
Prove that: \(\frac{\sin x-\sin y}{\sin x+\sin y}=\tan \left(\frac{x-y}{2}\right) \cot \left(\frac{x+y}{2}\right)\)
Solution:
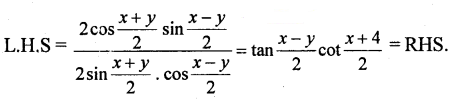
Question 19.
Find the equation of the parabola given that vertex (0, 0) and directrix x = -5.
Solution:
The curve turns right side and a = 5.
y2 = 20x is equation of the parabola.
Question 20.
Find the value of K, if the function 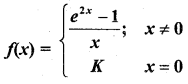 is continuous at x = 0.
is continuous at x = 0.
![]()
Question 21.
Find \(\frac{d y}{d x}\) if y = xx.
Solution:
Taking logm both sides
log y = log xx
log y = x log x
diff w.t.r x
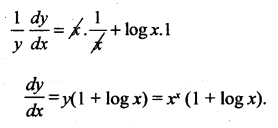
Question 22
If the displacement ‘s’ at any time ‘t’ is given by s = \(\sqrt{1-t}\). Show that the velocity is inversely proportional to the displacement.
Solution:

Question 23.
Evaluate : \(\int \frac{3 x^{8}}{1+x^{9}} d x\)
Solution:
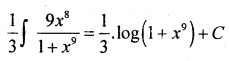
![]()
Question 24.
Evaluate : \(\int_{0}^{\pi / 4} \sec ^{2} 3 x \cdot d x\)
Solution:
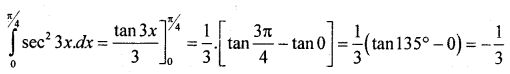
Part – C
III. Answer any Ten Questions: (10 × 3 = 30)
Question 25.
Prove that A2 – 4A – 5I = 0, where I = \(\left[\begin{array}{lll} 1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{array}\right]\) is the unit matrix and A = 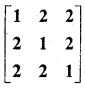
Question 26.
Prove that \(\left[\begin{array}{ccc}1 & 1 & 1 \\a & b & c \\b c & c a & a b\end{array}\right]\) = (a – b)(b – c)(c – a)
Solution:

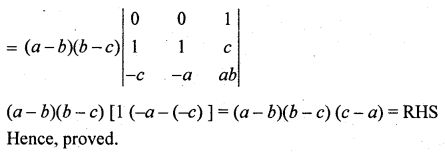
Question 27.
If a convex polygon has 170 diagonals, find the number of sides of the polygon.
Solution:
170 = \(n C_{2}\) – n
⇒ 170 = \(\frac{n(n-1)}{2}\) – n
⇒ 340 = n2 – 3n
⇒ n2 – 3n – 340 = 0
⇒ (n – 20)(n + 17) = 0
⇒ n = 20
![]()
Question 28.
A bag contains 10 gold and 8 silver coins. Two successive drawings of 4 coins are made. Find the probability that the first drawing will get 4 gold and second 4 silver coins if coins are replaced before the second trial.
Solution:
4 coins can be drawn from 18 coins in \(^{18} \mathrm{C}_{4}\) ways.
4 goldcoins can be drawn in \(^{10} \mathrm{C}_{4}\) ways.
P(4 gold coins in Ist draw) = \(\frac{_{10 \mathrm{C}_{4}}}{18 \mathrm{C}_{4}}\)
Since 4 coins are replaced in the second draw again 4 coins are drawn from 18 coins in \(^{18} \mathrm{C}_{4}\) ways.
Silver coins can be selected in \(^{8} \mathrm{C}_{4}\) ways.
P (4 silver coins in II draw) = \(\frac{^{8} C_{4}}{^{18} C_{4}}\)
P (4 gold and 4 silver) = \(\frac{^{10} \mathrm{C}_{4}}{^{18} \mathrm{C}_{4}} \times \frac{^{8} \mathrm{C}_{4}}{^{18} \mathrm{C}_{4}}\)
Question 29.
5 men each working 9 hours a day can finish a work in 30 days. How many men are required to finish eight times the work in 25 days, each working 8 hours a day?
Solution:
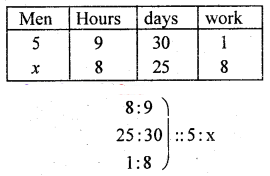
more men fewer hours → Inverse proposition
more men fewer days → Inverse proposition
more work, more men → Direct proportion
x = \(\frac{5 \times 9 \times 30 \times 8}{8 \times 25 \times 1}\) = 54 men
54 men are required to finish the work.
![]()
Question 30.
Banker’s gain on a bill due after 6 months at 4% p.a is ₹ 24. Find TD, BD and bill amount.
Solution:
Given B.G = 20, t = 6 months = \(\frac {1}{2}\) yr, r = 4% = 0.04
(i) B.G = T.D. tr
20 = TD (0.5 × 0.04)
TD = \(\frac{20}{0.020}\) = Rs. 1000
(ii) B.D = T.D + B.G = 1000 + 20 = 1020
(iii) F = \(\frac{B . D \times T . D}{B . G}\) = \(\frac{1020 \times 100}{20}\) = 51000
Question 31.
Prashanth sold 25 Biocon shares when the market price was ₹ 400 per share. He then bought 10 Reliance shares which were selling at ₹ 800 per share. Brokerage for each transaction was 0.25%. The balance amount he gave to his daughter Sonu for shopping. How much did Sonu receive?
Solution:
Amount received by selling Biocon shares = 25 × 400 = ₹ 10,000.
Brokerage = \(\frac {0.25}{100}\) × 10,000 = ₹ 25
Net Amount Received = 10,000 – 25 = ₹ 9,975
Amount paid for Reliance shares = 800 × 10 = ₹ 8, 000
Brokerage = \(\frac {0.25}{100}\) × 8000 = ₹ 20
Net Amount paid = 8000 + 20 = ₹ 8020
Balance Amount = 9975 – 8020 = ₹ 1955
Amount paid to Sonu for shopping is ₹ 1955.
Question 32.
A colour TV is marked for sale for ₹ 17,600 which include sales tax at 10%. Calculate the sales tax in ₹?
Solution:
S.P = ₹ 17,600, S.T% = 10%, S.T. = ?
Let M.P = x
Total amount to be paid (S.P) = M.P + ST% of M.P
17,600 = x + 10% of x
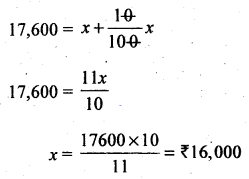
S.T = S.P – M.P = 17,600 – 16,000 = ₹ 1,600.
![]()
Question 33.
If one end of the diameter of the circle x2 + y2 + 2x + 6y – 22 = 0 is (3, -7). Find the co-ordinates of the other end point.
Solution:
Centre of the given circle = (-1, -3)
Oneendisgivenas A(3, -7)
Let the other end be B(x, y) = ?
W.K.T. centre = mid point of the diameter
⇒ (-1, -3) = \(\left(\frac{3+x}{2}, \frac{-7+y}{2}\right)\)
⇒ 3 + x = -2, -7 + y = -6
⇒ x = -5, y = 1
The other end of the diameter = B(-5, 1).
Question 34.
Differentiate “sin x” from the first circles.
Solution:
Let y = f(x) = sin x, then
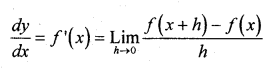
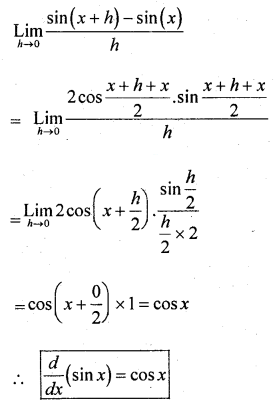
Question 35.
Find the maxima and minima of the function f(x) = 3x3 – 9x2 – 27x + 30
Solution:
Given f(x) = 3x3 – 9x2 – 27x + 30 …….. (1)
f'(x) = 9x2 – 18x – 27 …….. (2)
f”(x) = 18x – 18 ……. (3)
for a function to be maximum or minimum f'(x) = 0
⇒ 9x2 – 18x – 27 = 0
⇒ x2 – 2x – 3 = 0
⇒ (x – 3)(x + 1) = 0
⇒ x = 3 or -1
Case I: Put x = 3 in Eqn. (3).
f”(x) = 18 × 3 – 18 = 36 > 0
f(x) is minimum at x = -1 and minimum value is given by
f(3) = 3(3)3 – 9(3)2 – 27(3) + 30 = -51
Case II :
Put x = -1 in equation (3)
f”(-1) = 18(-1) – 18 = -36 < 0
f(x) is maximum, at x = -1 and maximum value is given by
f(-1) = 3(-1)3 – 9(-1)2 – 27(-1) + 30 = -3 – 9 + 27 + 30 = 45
![]()
Question 36.
A man 2 mt. height walks at a uniform speed of 6 km/hr away from the lamp post 6 mt high. Find the rate at which the
(i) length of his shadow increase
(ii) Rate at which the tip of the shadow is moving.
Solution:
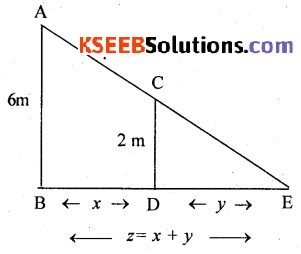
Given the rate of man walking \(\frac{d x}{d t}\) = 6 km/hr
Rate of shadow length increase = \(\frac{d y}{d t}\) = ?
Rate of tip of the shadow increasing = \(\frac{d z}{d t}\) = ?
∆ABE and ∆CDE are similar
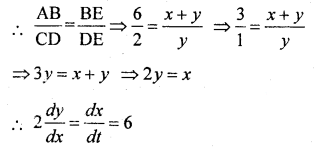
Rate of increase of length of shadow = \(\frac{d y}{d t}=\frac{6}{2}\) = 3 km/hr
Again Z = x + y
Differentiate w.r. to x.
\(\frac{d z}{d t}=\frac{d x}{d t}+\frac{d y}{d t}\) = 6 + 3 = 9 km/hr
Rate at which tip of shadow is moving = 9 km/hr
Question 37.
Evaluate : ∫x cos x dx
Solution:
∫x(sinx) – ∫sin x dx
= x sin x – (-cos x) + C
= x sin x + cos x + C
![]()
Question 38.
Evaluate:\(\int \frac{1}{1+\cos x} d x\)
Solution:
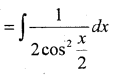
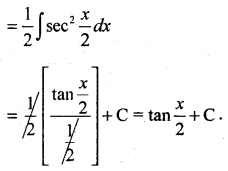
Part – D
IV. Answer any six questions: (6 × 5 = 30)
Question 39.
Find the coefficient of x5 in the expansion of \(\left(x+\frac{1}{x^{2}}\right)^{17}\)
Solution:
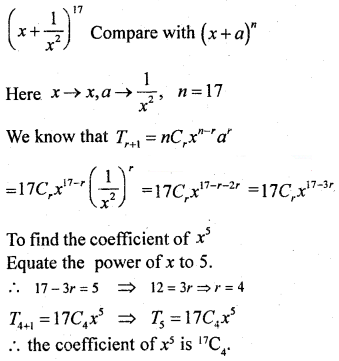
Question 40.
Resolve into partial fractions: \(\frac{3 x+2}{(x-2)(x+3)^{2}}\)
Solution:
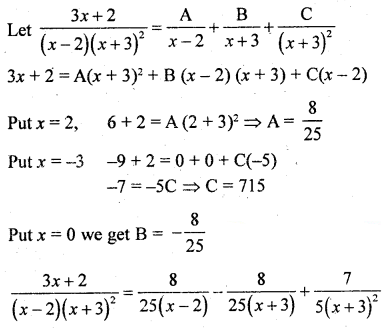
Question 41.
Prove that ~(p → q) = p∧~ q
Solution:

Question 42.
A jar contains two liquids A and B in the ratio 7 : 5 when 9 litres of the mixture is drawn and the jar is filled with the same quantity of B, the ratio of A and B becomes 7 : 9. Find the quantity of A in the jar initially.
Solution:
Let the quantities of the two liquids be 7x and 5x, 9 litres are drawn and the jar is filled with the same quantity of B i.e. 5.
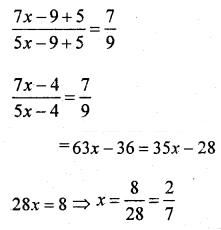
Initial quantity Of liquid A = 7x = 7 × \(\frac{2}{7}\) = 2 litres
![]()
Question 43.
XYZ company supplies water tankers to the Government. The first water tanker takes 20,000 labour hours. The government auditors suggest that there should be a 90% learning effect rate. The management expects an order of 8 water tankers in the next year. What will be the labour cost the company will incur at the rate of ₹ 20 per hour?
Solution:
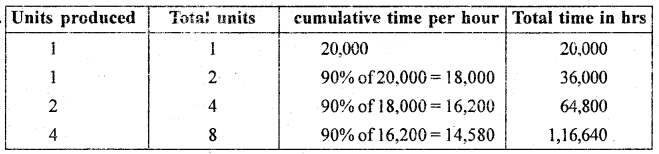
Total labour hrs produced = 1,16,640
Total labour cost produced for 8 water tankers at the rate of 20/- hr = 1,16,640 × 20 = 23,32800
Question 44.
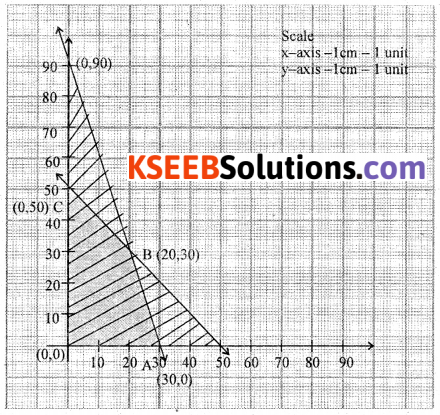
Solve the following L.P.P graphically maximise z = 60x + 15y subject to the constraints x + y ≤ 50, 3x + y ≤ 90, x ≥ 0, y ≥ 0.
Solution:
Consider x + y = 50
Put x = 0, y = 50, (0, 50)
Put y = 0, x = 50 (50, 0)
3x + y = 90
x = 0, y = 90, (0, 90)
y = 0, x = 30 (30, 0)
OABC is the feasible region.

Question 45.
Prove that sin 20° sin 40° sin 60° sin 80° = \(\frac{3}{16}\)
Solution:
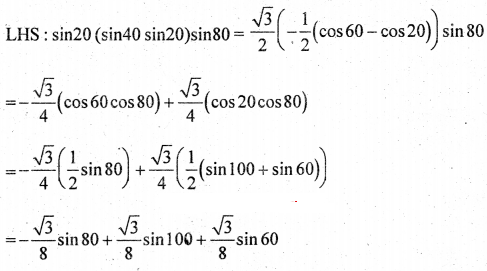
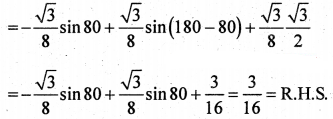
![]()
Question 46.
Find the equation of the circle passing through the points (1, 2) and (2, 1) and has its centre on the y-axis.
Solution:
Let the required equation of the circle be x2 + y2 + 2gx + 2fy + c = 0
It passes through the points (1, 2) and (2, 1) and the centre lies on y-axis
⇒ g = 0 ……. (1)
(1, 2) ⇒ 12 + 22 + 2g(1) + 2f(2) + C = 0
⇒ 4f + c + 5 = 0 ……..(2)
(2, 1) ⇒ 22 + 12 + 2g(2) + 2f(1) + c = 0
⇒ 2f + c + 5 = 0 …….. (3)
Eqn. (3) – Eqn. (2) gives 2f = 0 ⇒ f = 0
put g = 0 and f = 0 in eqn (3) gives c = -5 ⇒ c = -5
the required equation of the circle is x2 + y2 + 2(0)x + 2(0)y – 5 = 0
⇒ x2 + y2 – 5 = 0
Question 47.
If y = (x2 + a2)6 prove that (x2 + a2)y2 – 10xy1 – 12y = 0
Solution:
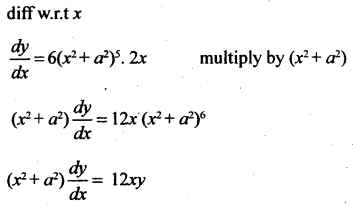
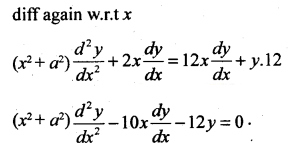
Question 48.
Find the area bounded by the parabola y2 = 4x and the line y = 2x – 4.
Solution:
The given parabola is y2 = 4x ……… (1)
The given line is y = 2x – 4 and x = \(\frac{y+4}{2}\) ……. (2)
Solving (1) and (2) we get \(\frac{y^{2}}{4}=\frac{y+4}{2}\)
⇒ y2 – 2y – 8 = 0
⇒ (y + 2)(y – 4) = 0
⇒ y = -2 or 4
The points of intersection are A(1, 2) and B(4, 4)
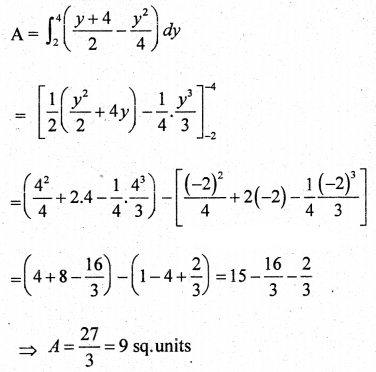
Part – E
V. Answer any one questions. (1 × 10 = 10)
Question 49.
(a) Transport corporation operates bus service between two villages. Date regarding the passenger traffic during the first three days of the week is given below’ along with the total revenue. The data does not include bus fare charged per child, senior citizen and adults.

Find the bus fare charged per child, senior citizen and per adult by using matrix method.
Solution:
Let x, y & z denote the raters of commission in Rupees/unit for the child, senior citizen and per adult respectively. Then the data given can be expressed as a system of linear equations.
100x + 100y + 200z = 900
300x + 200y + 100z = 1000
100x + 200y + 300z = 1400
or
x + y + 2z = 9
3x + 2y + z = 10
x + 2y + 3z = 14
Solve these equations by Matrix Method.


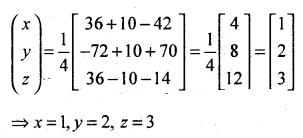
(b) A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he returns 40 metres from the bank, he finds the angle to be 30°. Find the height of the tree and the breadth of the river.
Solution:
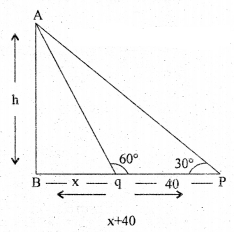
Let AB = height of the tree = h
Breadth of the river = x mts
From ∆AQB, tan 60° = \(\frac{\mathrm{AB}}{\mathrm{QB}}\)
⇒ √3 = \(\frac{h}{x}\)
⇒ h = x√3 …… (1)
From ∆APB, tan 30° = \(\frac{\mathrm{AB}}{\mathrm{PB}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{40+x}\)
⇒ 40 + x = √3.h
⇒ 40 + x = 3x
⇒ 40 = 2x
⇒ x = 20 mts
h = x√3 = 20√3 mts
Hence height of tree = 20√3 mts, Breadth of the river = 20 mts
![]()
Question 50.
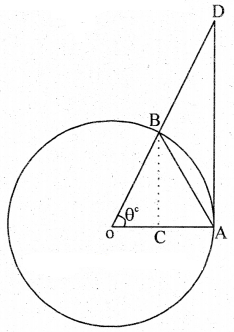
(a) If the angle q is measured in radians then prove that \(\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta}=1\)
Solution:
Let ‘O’ the centre of unit circle, assume that θ is measured in positive radians
Let ∠AOB = θc, from A, draw AD is ⊥ to OA, meeting OB produced to D, therefore OA = OB = radians
From the diagram we have area of ∆AOB = area of sector AOB = area of ∆AOD
area of ∆AOB ≤ area of sector ∆AOB ≤ area of ∆AOD
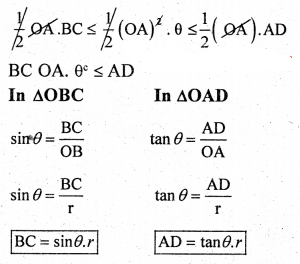

(b) Using binomial theorem find the value of (1.01)5 corrected up to four.
Solution:
(1 .01)5
= (1 + 0.1)5
![]()
= 1 + 5(0.01) + 10(0.001) + 10(0.000001) + Neglect the next terms
= 1 + 0.05 + 0.001 + 0.00001
= 1.0510 correct upto 4 decimals