Students can Download 1st PUC Statistics Model Question Paper 1 with Answers, Karnataka 1st PUC Statistics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Statistics Model Question Paper 1 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Note :
- Graph sheets and statistical tables will be supplied on request.
- Scientific calculators may be used.
- All working steps should be clearly shown.
Section-A
I. Answer any TEN of the following questions. (10 × 1 = 10)
Question 1.
How did the world statistics originate
Answer:
The word statistics originates from the Latin word ‘status’ or a German word ‘statistik’.
Question 2.
Define the term statistical enquiry.
Answer:
Search for the knowledge through statistical methods is Statistical enquiry.
Question 3.
What is classification?
Answer:
Classification is the process of arranging the data into groups or classes according to common characteristics of the data.
Question 4.
What is the correction factor used in the formation of frequency distribution?
Answer:
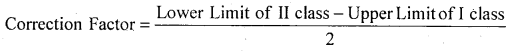
It is used to convert in elusive, classes into exclusive closses.
Question 5.
Which measure of control tendency is located from Histogram?
Answer:
Mode is located from histogram.
![]()
Question 6.
What is frequency density?
Answer:
The frequency per unit of class interval is the frequency density

Question 7.
Find the mode: 4, 8, 5, 6, 4, 9, 3, 4.
Answer:
Here mode(Z) = 4. Repeated more number of times.
Question 8.
Write down the formulae of Q3 for a continuous data.
Answer:
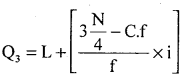
Question 9.
What is correction between variables.
Answer:
Correlation is said to exists between two variables, if they vary directly or indirectly together.
Question 10.
What is extrapolation?
Answer:
Extrapolation is a procedure of estimating the unknown value of dependent variable for a given value of independent variable which is outside the limits or the range of the independent variable.
Question 11.
Define equally likely events in Probability.
Answer:
Outcomes of a random experiments are said to be equally likely if they have equal chance of occurrence.
Question 12.
If E(x) = 3, Find E(3x)
Answer:
E(3x) = 3, E(x) = 3 × 3 = 9.
Section- B
IV. Answer any TEN of the following questions. (10 × 2 = 20)
Question 13.
Define discrete variable and given example.
Answer:
A variable which assumes a specific values in the given range discrete variable.
Ex: Number of children/number of rooms in a college.
Question 14.
Mention any two causes of errors in statistical investigation.
Answer:
- Errors of origin
- Errors of manipulation.
Question 15.
What do you mean by exclusive class intervals? Give an example.
Answer:
In a class, if in a class lower limit is included and upper limit is excluded but included in the next class is a exclusive class interval:
Ex: (0- 10), (10-20), (20-30).
Question 16.
What are source and foot notes of a table?
Answer:
Source is written just below the foot note in a table, which indicate the data obtained from publications, books, journals etc.
Footnote is to indicate the errors, ommissions, remarks, abrevations of the data in the table.
Question 17.
Mention any two rules of formation of a frequency distribution.
Answer:
- The lower limit of the first class is either’O’or a multiple of 5.
- Exclusive classes should be formed for better continuity.
![]()
Question 18.
Mention the different types of diagrams.
Answer:
- Simple Bar diagram
- Multiple Bar diagram
- Component Bar diagram
- Percentage Bar diagram.
Question 19.
Find the GM. of 4,25.
Answer:
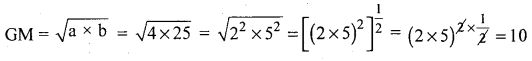
Question 20.
For a data if Q3 = 78 and = Q1 Find Quartile deviation.
Answer:
Quartile deviation. = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}=\frac{78-32}{2}=23\)
Question 21.
Writed down two properties of correlation coefficient.
Answer:
The coefficient of correlation is
- Independents of units of measurement
- Independent of orgin and scale.
Question 22.
If in a 2 × 2 contingency table the frequencis of first order (A) = 130 and (B) = 120 then find the total frequency.
Answer:
In a 2 × 2 contingeven table N – is frequency of zero order, is obtained as N = (A) + (B)
∴ N = 130 + 120 = 250
Question 23.
Find the probability of getting an even number when die is thrown once.
Answer:
P (getting anewen number) = \(\frac { m }{ n }\) = \(\frac { 3 }{ 6 }\) = \(\frac { 1 }{ 2 }\)
Question 24.
If E(x) = 3.5 E(y) = 2 and E(xy) = 8 find cov (x, y).
Answer:
cov (x, y) = E(x y) – E(x). E(y) = 8 – 3.5 × 2 = 8 – 7= l
Section- C
IV. Answer any EIGHT of the following questions. (8 × 5 = 40)
Question 25.
Write the characteristics statistics.
Answer:
The characteristics of statistis are :
- Aggregates of facts
- Affected to a marked extent by multiplicity of causes.
- Numerically empressed.
- Enumerated or estimated according to a reasonable standards of accuracy.
- Collected in a systematic manner
- Collected for predetermined purpose
- Should be placed in relation to each other
Question 26.
Explain direct and indirect method of collection of primary data with relative merits and demerits.
Answer:
1. Direct personal observation; In this method the investigator, collects the required information by personal observation of the units, through the enumerator, from the informants. This methods is successively employed Where the field of enquiry is confidential, small, greater accuracy and sufficient time is available.
Merits: This method is most reliable, accurate and confidential.
Demerits: This method is expensive, time consuming and this method becomes difficult where the enquiry is field of large. In this method there is chance of personal bias in collection of data, needs trained and skilled personnel.
2. Indirect oral interview: This method is applied, where the required information from the informant is not possible to obtain by direct interview method. In this method the investigator/enumerator approaches the witnesses or third parties, who are capable to supply the necessary information about the first person/informant.
Merits: This method is simple, convenient, free from bias and successively employed by News paper, Broadcasting, Investigating agencies.
Demerits: In this method there is an ample scope of bias by influencing the enquiry by the third person.
Question 27.
Prepare a blanks table to show the population of a town according to
(i) Se.Y-men, women
(ii) Literacy – literates, illiterates
(iii) Employment – Employed, unemployed.
Answer:
Table showing the population of a town according to sex, literacy and employment
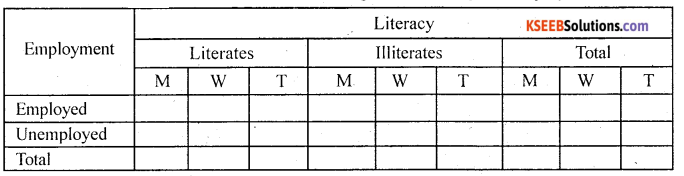
Foot Note: M – men, W – Women, T – Total
Source:
![]()
Question 28.
Following data relating to export and import (₹ in crores) for the year 2005-2006.
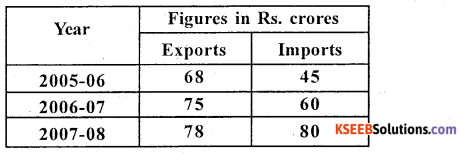
Answer:
Draw multiple bar diagram
Multiple bar diagram of export axed imports (₹ crores)
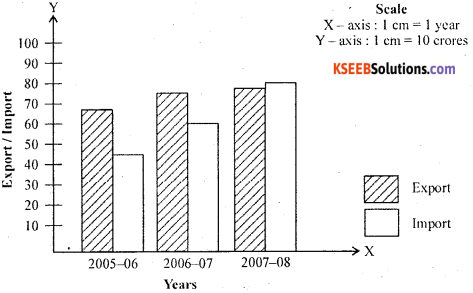
Question 29.
Compute Arithmetic mean for the following

Answer:
Let X (C.l) and f be the income and number of workers.
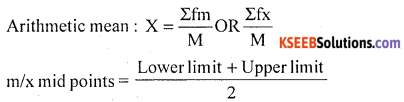
X̄ = \(\frac { 458 }{ 54 }\) = 10.409
Mean income of worker is 10.409 (000’s ₹)
Question 30.
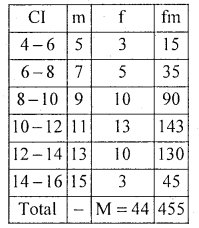
Compute Karl Pearson’s coefficient of correlation from the following data

Answer:
Let X and Y be demanc and supply
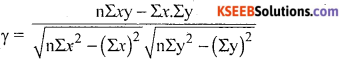
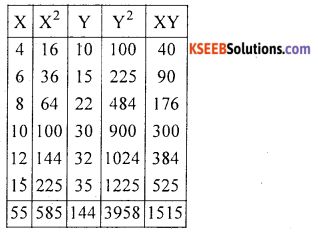
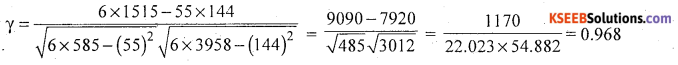
There exists high degree positive correlation between demand and supply
![]()
Question 31.
Following data relates to a bivariate of x and y : n = 10; Σx = 25, Σy = 40, the regression coefficients of x on y and y on x are 1.203 and 0.42. Find the most probable value of x when y = 3.8.
Answer:
![]()
bxy = 1.230, byx = 0.42
To find X when y = 3.8
Regression equation of x only is
(x.x̄) = bxy (y – ȳ)
x – 2.5 = 1.203 (3.8 – 4)
x – 2.5 = 1.203 × (-0.2)
= -0.2406 + 2.5
x = 2.2594
Question 32.
In a class of 80 students, number of married were 32. But 24 of failed students 10 are married. Find whether marriage and failure of students are independent.
Answer:
Let A married and B failed students and α – unmarried β – passed students.
The 2 × 2 contingency table is :

There exists very low degree of association between marriage and failure, which means independent.
Question 33.
From the following table interpalate missing value:

Answer:

Since 4 known valus of y are given the binomial expansion 4th leading difference
Since 4 known valus of y are given the binomial expansion 4th leading difference
Δ4 = 0 ie., (y – l)6 = y4 – 473 + 6y2 – 47y1+ 70 = 0
22 – 4 × 18 +6y2 – 4 × 16+ 14 = 0
22 – 72 + 6y2 – 64 +14 = 0
-100 – 6y2 = 0
y2 = \(\frac { 100 }{ 6 }\) = 16.7
Question 34.
State and prove the addition theorem of prabability forany two mutually exclusive events:
Answer:
Statement: Let A and B be two mutually exclusive events with respective probabilities P(A) and P(B). Then the probability of occurrence of atleast one of the events is
P (A ∪ B) = P(A) + P(B)
Proof: Arandom experiment results ‘n’ exhaustive mutually exclusive out comes, of which m and m7 outcomes are favorable to events A and B.
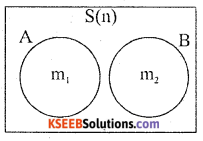
Then P(A) = \(\frac{m_{1}}{n}\)
P(B) = \(\frac{m_{2}}{n}\) Results (1)
Here the favourable events to occur either A or B are (m1 + m2)
![]()
P (A ∪ B) = P(A) + P(B)
Hence the proof.
![]()
Question 35.
If in a class of 4 boys and 3 girls, find the probability of selection 2 students are (i) boys and (ii) girls.
Answer:
n = 2 students can be selects from 4 boys and 3 girls = 7C, ways = 21 ways.
Let P(A) = P(Boys selected)
P(B) = P (girls selected)
(i) p(A) = \(\frac { m }{ n }\) = \(\frac { 412 }{ 712 }\) = \(\frac { 6 }{ 21 }\)
(ii) P(B) = \(\frac { 312 }{ 712 }\) = \(\frac { 3 }{ 21 }\)
Question 36.
A random varable x assumes the vallues 0, 1 and 2 with respective probabilities \(\frac { 1 }{ 4 }\), \(\frac { 2 }{ 4 }\) and \(\frac { 1 }{ 4 }\) Find E(x).
Answer:
The given probability distribution of x is
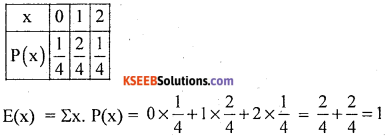
Section- D
IV. Answer any TWO of the following questions. (2 × 10 = 20)
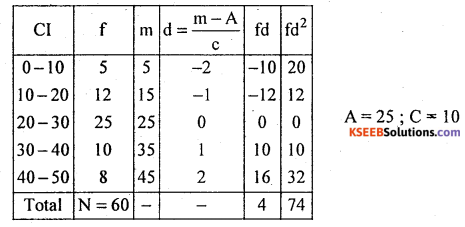
Question 37.
From the following frequency distribution find the coefficient of variation.

Answer:
Let X (Cl) and f be the marks and number of students

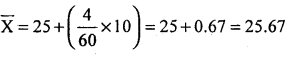

![]()
Question 38.
Calculate Bowley’s coefficient of skewness for the following data

Answer:
Let X (C.I) and f be the profit and no of firms
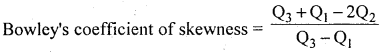
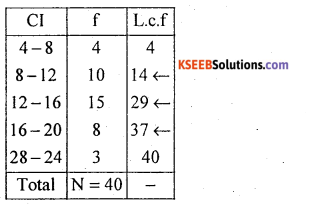

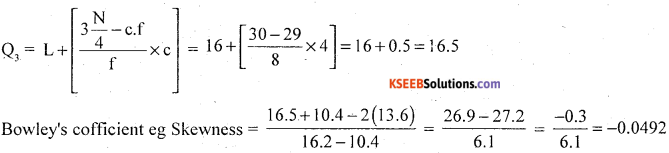
The distribution is very low Negative skewness.
Question 39.
For the following Bivariate, frequence distribution compute the Karl person’s n t eg correction and interpret.
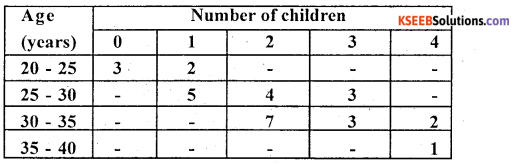
Answer:
Let x and y be the age and number of children

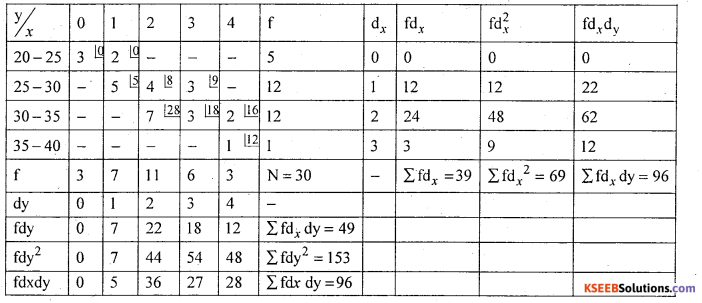

There exists a high degree positive correlations between age and number of children
![]()
Question 40.
For the following bivariate probability distribution find -γxy
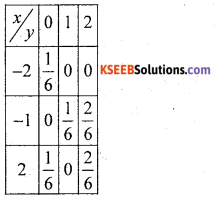
Answer:


Section-E
V. Answer any TWO of the following questions. (2 × 5 = 10)
Question 41.
Intossing a coin game, person will get ₹. 5 if he get head other wise he loses ₹2. Find the expected amount.
Ans.
Let x denoted the amount which takes the values 5 and -2 with respective Probabilitis each:
His expceted amount is
E(x)=ΣxP(x) = 5 × \(\frac { 1 }{ 2 }\) – 2 × \(\frac { 1 }{ 2 }\) = ₹1.50/-
Question 42.
For the following ages of kg classchildren prepare a frequency table.
Age (in years) : 2.5, 3.2, 2.8, 2.4, 2.3, 2, 3.1, 3.6, 4.1, 4.9, 3,6, 4.2, 3.7, 3.5, 2.7, 2.8, 2.7, 2.9, 3.4, 4.5, 4.8, 4.6, 4.3, 3.2.
Answer:
The frequency table of ages of KG class children (in years)

![]()
Question 43.
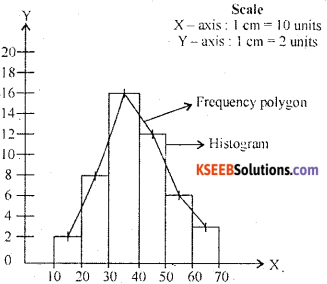
Draw frequency polygon based on historgram for the following data.

Answer:
Histagram and frequency polygon
Question 44.
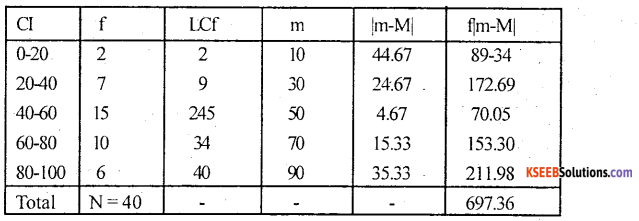
For the following data compute mean deviation from median.

Answer: