You can Download Chapter 8 Gravitation Questions and Answers, Notes, 1st PUC Physics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Physics Question Bank Chapter 8 Gravitation
1st PUC Physics Gravitation Textbook Questions and Answers
Question 1.
Answer the following:
1. You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
2. An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?
3. If you compare the gravitational force on the earth due to the sun to that due to the moon, you would find that the Sun’s pull is greater than the moon’s pull, (you can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the moon’s pull is greater than the tidal effect of the sun. Why?
Answer:
1. No, It is impossible to screen the influence of gravitational force. This is mainly because unlike other forces the gravitational force acts on a body independent of the material medium or the status of the body on which it is acting or that of the body due to which it is present.
2. Yes, If the mass of the space station is large enough then the astronaut can detect gravity acting on him.
3. The tidal effect is inversely proportional to the cube of the distance while the gravitational force is inversely proportional to the square of the distance. Since the distance between sun and earth is much greater than that between the moon and earth, the effect observed due to the moon is more that due to the sun.
Question 2.
Choose the correct alternative:
1. Acceleration due to gravity increases/decreases with increasing altitude.
2. Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density).
3. Acceleration due to gravity is independent of the mass of the earth/ mass of the body.
4. The formula – G Mm(1/r2 – 1/r1) is more/less accurate than the formula mg(r2 – r1) for the difference of potential energy between two points r2 and r1 distance away from the centre of the earth.
Answer:
1. Decreases.
The value of acceleration due to gravity at a height ‘h’ above the ground ‘gh’ is given by,
gh = \(g\left[1-\frac{2 h}{R_{e}}\right]\), where Re is radius of Earth. Therefore gh decreases with an increase in height.
2. Decreases.
The value of acceleration due to gravity at a depth ‘d’ below the ground (gd), is given by, gd = \(g\left[1-\frac{d}{R_{e}}\right]\), where Re is the radius of earth. This shows that with an increase in the value of ‘d’ i the value of gd decreases.
3. Mass of the body
The acceleration due to gravity of any planet of mass ‘M’ and radius ‘R’ is given by, g = \(\frac{G M}{R^{2}}\), where, G is the universal gravitational constant. So, the value of ‘g’ is dependent on the mass of the earth but independent of mass of the body.
4. More accurate
The gravitational potential energy of any point at a distance ‘r’ from the centre of the earth is
V (r) = \(-\frac{G m M}{r}\)
So, Potential Energy difference
= V(r2) – V(r1)

= gm (r2 – r1)
= mgr2 – mgr1
(Assuming r2 – r1 ≈ R2)
Thus -GmM \(\left(\frac{1}{r_{2}}-\frac{1}{r_{1}}\right)\) is a more accurate relation.
Question 3.
Suppose, there existed a planet that went around the sun twice as fast as the earth. What would be its orbital size as compared to that of the earth?
Answer:
Let TE be the time taken for one revolution by earth and Tx be that by the planet. Similarly, let RE be the orbital radius of earth and Rx be that of the planet.
From Kepler’s 3rd Law of planetary motion, R3 ∝ T2
⇒ \(\frac{R_{x}^{3}}{R_{\varepsilon}^{3}}=\frac{T_{x}^{2}}{T_{E}^{2}}\)
Rx = RE\(\left(\frac{T_{x}}{T_{E}}\right)^{2 / 3}\)
⇒ Rx = (0.5)2/3 RE
[∵ give that TE = 2TX]
⇒ Rx = (0.63) RE
So, the orbital size of the planet is lesser by a factor of 0.63.
![]()
Question 4.
One of the satellites of Jupiter has an orbital period of 1.769 days and the radius of the orbit is 4.22 × 108m. Show that the mass of Jupiter is about one-thousandth that of the sun.
Answer:
For the satellite around Jupiter
T10 = 1.769 days
R10 = 4.22 × 108m
For earth around sun
Te = 365.25 days
Re = 1.496 × 1011m
We know that,
M = \(\frac{4 \pi \mathrm{R}^{3}}{\mathrm{GT}^{2}}\)
⇒ \(\frac{M_{S}}{M_{J}}=\left(\frac{1.496 \times 10^{11}}{4.22 \times 10^{8}}\right)^{3} \times\left(\frac{1.769}{365.25}\right)^{2}\)
= 1045.039
= 1000
Thus mass of Sun is about thousand times Mass of Jupiter.
Question 5.
Let us assume that our galaxy consists of 2.5 × 1011 stars each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic centre take to complete one revolution? Take the diameter of the Milky Way to be 105 ly.
Answer:
Number of stars in our galaxy = 2.5 × 1011
Mass of each star = 1 solar mass
= 2 × 1030 kg
⇒ Mass of our galaxy
= 2.5 × 1011 × 2 × 1036 kg
= 5 × 1041 kg
Diameter of milky way = 105 ly
d = 105 × 3 × 108 ms-1 × 1yr
The distance of the star = radius of its orbit = 5 × 104 ly.
Therefore, the time period of the revolving star is given by,

T2 = 1.259 × 1017 yr2
T = 3.549 × 108 yrs
It takes about 3.55 × 108 years to complete one revolution for a star around the milky way.
Question 6.
Choose the correct alternative:
- If the zero of potential energy is at infinity, the total energy of an orbiting satellite is negative of Its kinetic/ potential energy.
- The energy required to launch an orbiting satellite out of earth’s gravitational influence is more/less than the energy required to project a stationary object at the same height (as the satellite) out of earth’s influence.
Answer:
1. Kinetic energy
The potential energy of a satellite rotating in its orbit is zero. The total energy of a system is the sum of its kinetic energy (+ve) and potential energy. Since the earth satellite system is a bound system. The satellite has a negative total energy. So, the energy of the satellite is the negative of its kinetic energy.
2. Less
An orbiting satellite has more energy than a stationary object at the same height. This additional energy is provided by the orbit. It requires lesser energy to make it move out of the earth’s influence than a stationary object.
Question 7.
Does the escape speed of a body from the earth depend on?
- the mass of the body,
- the location from where it is projected,
- the direction of projection,
- the height of the location from where the body is launched?
Answer:
Escape velocity of a body from earth is given by v = \(\sqrt{2 g R}\).
g = Acceleration due to Gravity.
R = Radius of earth.
1. No.
Escape velocity is independent of mass of the object.
2. No.
Assuming the value of g is the same in all the locations, it is independent of location of projection.
3. No.
The direction of projection is also immaterial as long as it is projected with the velocity above ground.
4. Yes.
It depends on the gravitational potential energy which depends on the height. Since g changes with height. The escape velocity also depends on height.
Question 8.
A comet orbits the sun in a highly elliptical orbit. Does the comet have a constant?
- linear speed,
- angular speed,
- angular momentum,
- kinetic energy,
- potential energy,
- total energy throughout its orbit?
Neglect any mass loss of the comet when it comes very close to the Sun.
Answer:
- No, linear speed varies from point to point in the orbit.
- No, angular speed varies from point to point in the orbit.
- Yes, angular momentum is conserved at any point
- No, kinetic energy varies as the speed varies.
- No, potential energy varies as distance, from Sun varies.
- Yes, the total energy of the system is always constant.
![]()
Question 9.
Which of the following symptoms is likely to afflict an astronaut in space
- swollen feet,
- swollen face,
- headache,
- orientational problem.
In the following two exercises, choose the correct answer from among the given ones:
Answer:
- No, swollen feet will not affect the astronaut as the astronaut feels weightlessness and legs do not support the weight.
- Yes, since most of the sense organs are on the face astronaut will feel its effect.
- Yes, headaches are not affected by gravity.
- Yes, orientation is necessary for doing any work, & without gravity also is necessary.
Question 10.
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see the following figure).
1. a,
2. b,
3. c,
4. 0
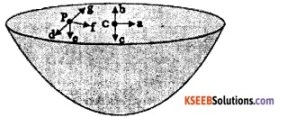
Answer:
The answer is (3) c.
The gravitational intensity at any point is defined as the negative of the potential gradient i.e., \(\left(-\frac{\mathrm{dv}}{\mathrm{dr}}\right)\)
At any point inside the spherical shell, the value of gravitational potential is constant implying the intensity is zero.
So, intensity at all points inside is zero. Since the upper half is cut off there is no attractive force on the upper portion to pull if upwards. So effectively the net force is downwards along c.
Question 11.
For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow.
- d,
- e,
- f,
- g
Answer:
Since, the gravitational intensity is defined as the negative of the gradient of gravitational potential i.e., \(\left(-\frac{\mathrm{dv}}{\mathrm{dr}}\right)\) and the value of gravitational potential inside the spherical shell is constant, the value of gravitational intensity is zero.
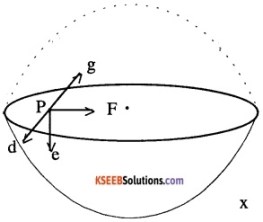
Consider any point p as shown, inside a sphere then the net gravitational intensity at that point is zero. If the upper half is cut off, the pull in the left and right side cancel each other just like the full sphere base but the pull upwards is missing. Thus the effective force is downwards along e.
Question 12.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 × 1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
Answer:
Let the distance from the earth to the point where gravitational force is to zero be x

Given that,
Mass of sum = Ms = 2 × 1030 kg
Mass of Earth = Me = 6 × 1024kg
Orbital radius = r = 1.5 × 1011 m
Now,
We know that, gravitational force ∝ \(\frac{M}{R^{2}}\)
Since, gravitational force of Earth = Gravitational force of Sun

x = 2.594 × 108 m
At a distance of about 2.6 × 105 km gravitational force is zero.
Question 13.
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 × 108 km.
Answer:
Given that
Orbital radius, r = 1.5 × 108 km
= 1.5 × 1011 m
We know that, Time for one revolution = 1 year
= 365.25 × 24 × 60 × 60s
Now,
M = \(\frac{4 \pi^{2} r^{3}}{G T^{2}}\)
G is universal gravitational constant.
⇒ M = \(\frac{4 \pi^{2} \times\left(1.5 \times 10^{8}\right)^{3}}{6.67 \times 10^{-11} \times\left(3.156 \times 10^{7}\right)^{2}}\)
= 2.005 × 1030 kg
≈ 2 × 1030 kg
The estimate mass of sun is 2 × 1030 kg
Question 14.
A Saturn year is 29.5 times the earth year. How far is the Saturn from the sun if the earth is 1.50 × 108 km away from the sun?
Answer:
Distance of earth from sun is the Earth’s orbital radius;
re = 1.5 × 108 km
= 1.5 × 1011 m
Time period of Earth = Te
Time period of Saturn = (29.5 × Te)
From Kepler’s 3rd Law of planetary motion
T2 ∝ R3
⇒ \(\frac{T_{s}^{2}}{T_{e}^{2}}=\frac{r_{s}^{3}}{r_{e}^{2}}\)
⇒ rs3 = \(\left(\frac{T_{s}}{T_{e}}\right)^{2}\) re3
= (29.5)2 × (1.5 × 1011)3
rs = (29.5)2/3 × 1.5 × 1011
= 1.432 × 1012 m.
![]()
Question 15.
A body weighs 63 N on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth?
Answer:
Weight of the body = 63 N = mg
Now at a certain height h, let the acceleration due to gravity be gn.
So, New weight = mgn
We know that gn = \(\frac{g}{\left(1+\frac{h}{R_{e}}\right)^{2}}\)
at a height of Re/2
gn = \(\frac{g}{\left(1+\frac{R_{e} / 2}{R_{e}}\right)^{2}}\)
= \(\frac{g}{(3 / 2)^{2}}\)
gn = \(\frac{4}{9}\) g
New weight = mgn= (mg) × \(\frac{4}{9}\)
= 63 × \(\frac{4}{9}\)
= 28 N
Question 16.
Assuming the earth to be a sphere of uniform mass density, how much would a body weigh halfway down to the centre of the earth if it weighed 250 N on the surface?
Answer:
Weight of body = 250 N
Now, at a depth d, let acceleration due to gravity be gd,
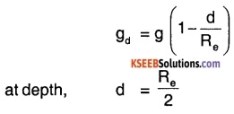
gd = g(1-1/2)
= g/2
New weight = mgd
= mg/2
= \(\frac{250 \mathrm{N}}{2}\)
= 125 N
Question 17.
A rocket is fired vertically with a speed of 5 km s-1 from the earth’s surface. How far from the earth does the rocket go before returning to the earth? Mass of the earth = 6.0 × 1024 kg; mean radius of the earth = 6.4 × 106 m; G= 6.67 × 10-11 N m2 kg-2.
Answer:
Initial velocity of the rocket,
Vi = 5 × 103 m s-1
Mass of the Earth, M = 6.0 × 1024 kg
Radius of the Earth, R = 6.4 × 106 m
Let the rocket be of mass, ‘m’ and reach an height ‘h’
Now, The initial energy of the rocket is given by,
Total initial energy (TEi) = Initial Kinetic Energy (KEi) + Initial Potential Energy (PEi)
KEi = \(\frac{1}{2}\) × m × Vi2
= \(\frac{m\left(5 \times 10^{3}\right)^{2}}{2}\) = 1.25 × m × 107
PEi = \(-\frac{G M m}{R}\)
⇒ TEi = 1.25 × m × 107 – \(\frac{\mathrm{GM}}{\mathrm{R}}\) × m
At the heighest point, the kinetic energy is 0. Total Energy at height ‘h’ (TEn) = PEn
⇒ TEn = \(-\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}\) × m
Since the total energy of system is conserved TEi = TEn

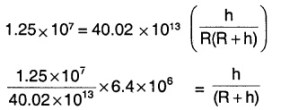
0.2 (R+h) = h
0.2 R = 0.8 h
h = (R/4) = 1.6 × 106m
The rocket goes 1.6 × 106 m from the surface pf the Earth and (6.4 + 1.6) × 106 = 8.0 × 106 m from the center of the Earth.
Question 18.
The escape speed of a projectile on the earth’s surface is 11.2 km s-1. A body is projected out with thrice this speed. What is the speed of the body far away from the earth? Ignore the presence of the sun and other planets.
Answer:
Escape velocity of projectile = 11.2 km s-1
Vesc =1.12 × 104 m s-1
Initial velocity of the projectile,
Vi =3 Vesc
= 3.36 × 104 m s-1
Let m be the mass of the projectile and Vf be the final velocity after it has escaped from the Earth’s gravitational field.
Initial Energy = KEi + PEi
KEi = \(\frac{1}{2}\) mVi2
By definition of Vesc, PEi = \(-\frac{1}{2} m V_{e s c}^{2}\)
Final Energy is = \(\frac{1}{2} m V_{f}^{2}\)
So, By conservation of energy
\(\left(-\frac{1}{2} m V_{e s c}^{2}\right)+\left(\frac{1}{2} m V_{1}^{2}\right)=\left(\frac{1}{2} m V_{f}^{2}\right)\)
⇒ Vf2 = Vi2 – V2esc

≈ 3.17 km s-1
Question 19.
A satellite orbits the earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the earth’s gravitational influence? Mass of the satellite = 200 kg; mass of the earth = 6.0 × 1024 kg; radius of the earth = 6.4 × 106 m; G = 6.67 × 10-11 N m2 kg-2.
Answer:
Mass of the satellite = 200 kg.
Mass of the Earth = 6.0 × 1024 kg
Radius of Earth = 6.4 × 106 m
Height of the satellite = 400 km
We knew that,
Orbital velocity of the satellite,
Vo = \(\sqrt{\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}}\)
So, Initial KE = \(\frac{1}{2} m V_{0}^{2}\)

Now we need to apply (- TEi) energy to force it out of the Earth’s influence.
So, Energy needed = \(\frac{\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}\)

= 5.9 × 109 J
Question 20.
Two stars each of one solar mass (2 × 1030 kg) are approaching each other for a head-on collision. When they are a distance 109 km, their speeds are negligible. What is the speed with which they collide? The radius of each star is 104 km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
Answer:
Mass of the Stars, M = 2 × 1030kg
Radius of the Stars, R = 104 km
= 107 m
Distance between Stars, d = 109 km
= 1012 m
Initial velocity almost 0, So KEi of each is 0. So, Initial potential energy
\(=-\frac{\mathrm{GMM}}{(\mathrm{d}+2 \mathrm{R})}=-\frac{\mathrm{GMM}}{\mathrm{d}}\)
[∵ d>>>R]
So, Initial Total Energy TEi = \(-\frac{\mathrm{GM}}{\mathrm{d}}\)
When the two Stars are about to collide let their velocity be V and separaion is 2R.
So, TE

By conservation of energy;
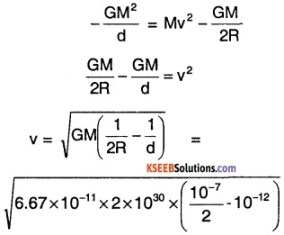
≈ \(\sqrt{6.67 \times 10^{12}}\)
v = \(\sqrt{6.67}\) × 106 m s-1
Question 21.
Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table. What is the gravitational force and potential at the midpoint of the line joining the centres of the spheres ? is an object placed at that point in equilibrium? if so, is the equilibrium stable or unstable?
Answer:
Mass of each sphere = 100 kg
Radius of each sphere = 0.1 m
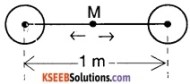
At the midpoint M, the gravitational pull by each sphere is exactly the same since they are identical spheres.
So, The gravitational force is zero.
The potential at M = – \(\frac{\mathrm{GM}}{(0.5)}-\frac{\mathrm{GM}}{(0.5)}\)
= – 4GM
= – 4 × 6.67 × 10-11 × 100
= – 2.668 × 10-8 J/kg
So, the potential at ‘M’ is – 2.67 × 10-8 J/kg
At object at M will be in equilibrium. Since mt force on it is zero. The equilibrium is unstable as a slight ctange in position of the mass, the net foce becomes non zero and it will move.
![]()
Question 22.
It’s you have learnt in the text, a geostationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth’s gravity at the sit* of this satellite? (Take the potential energy at infinity to be zero). Mas of the earth = 6.0 × 1024 kg, radius = 6400 km.
Answer:
Mass of the Earth = 6.0× 1024 kg
Radius of Earth = 6.4 × 106m.
Height of the satellite from surface of Earth is 36000 km = 3.6 × 107m
Distance of the satellite from centre of Earth is d = (3.6 × 107m + 6.4 × 106 m)
= 4.24 × 107 m
Gravitational potential due to Earth on the satellite is v = \(-\frac{G M}{d}\)
\(-\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{4.24 \times 10^{7}}\)
= – 9.438 × 107 J/kg
= – 9.4 × 107J/kg.
Question 23.
A star 2.5 times the mass of the sun and collapsed to a size of 42 km rotates with a speed of 1.2 rev. per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity? (mass of the sun = 2 × 1030 kg).
Answer:
Since the Star is rotating, there is a force pushing it outward (centrifugal force) and a force pulling it inwards, (gravitational force).
If gravitational force (FG) > Centrifugal force (Fc)
Then the object on the equator remains stuck on the star.
Mass of Star, M = 2.5 (MSun)
= 2.5 × 2 × 1030 kg
= 5 × 1030 kg
Radius of Star = 12 km = 1.2 × 104 m
⇒ FG = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}=\frac{6.67 \times 10^{-11} \times 5 \times 10^{30}}{\left(1.2 \times 10^{4}\right)^{2}}\)
= \(\frac{6.67 \times 5}{1.44}\) × 1011 × m
= 2.316 × 1012 × m N
Fc = mr ω2
Where, r = radius of Star = 12 km
ω = angular speed = 2 × π × (1.2)
⇒ Fc = m × 1.2 × 104 × (2.4π)2
= 6.82 × 105 × m N
Since Fc < FG the object is stuck to Star’s surface.
Question 24.
A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system? Mass of the space ship = 1000 kg; mass of the sun = 2 × 1030 kg; mass of mars = 6.4 × 1023 kg; radius of mars = 3395 km; radius of the orbit of mars = 2.28 × 108 km; G = 6.6 7 × 10-11 N m2 kg-2.
Answer:
Mass of Spaceship, ms = 1000 kg
Mass of mars Ms = 6.4 × 1023 kg;
Radius of mars rm = 3.395× 106 m
Radius of the orbit of Mars
= 2.28 × 108 km = 2.28 × 1011 m
Initial velocity of spaceship is = 0
So, the Total Initial Energy is only potential energy.
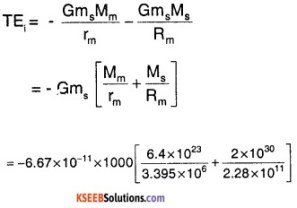
= – 6.67 × 10-8[1.88 × 1017 + 8.772 × 1018]
= – 6.67 × 8.96 × 1010
= – 5.976 × 1011 = – 6 × 1011 J
Question 25.
A rocket is fired ‘vertically’ from the surface of mars with a speed of 2 km s-1. If 20% of its initial energy is lost due to martian atmospheric resistance, how far will the rocket go from the surface of Mars before returning to it? Mass of mars = 6.4 × 1023 kg; radius of mars = 3395 km; G = 6.67 × 10-11 Nm2kg-2.
Answer:
Mass of Mars = 6.4 × 1023kg
Radius of Mars, R = 3.395 × 106 m.
Initial velocity of the rocket = 2 km s-1
= 2 × 103 ms-1
Let the mass of the rocket be m, then the initial kinetic energy is, \(\frac{1}{2}\) mv2
= \(\frac{1}{2}\) × m × (2 × 103)2
= 2 m × 106 J
Since 20% of the energy is lost due to atmost resistance, only 80% of energy is to be considered. Now,

Let the rocket reach a height ‘h’, at height h the velocity is 0. So, KEf = 0
and PEf = \(-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}\)
TEf = \(-\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}\) ….(2)
By conservation of Energy , (1) = (2)


0.1872 (R + h)= h
0.1272 R = 0.878 h
⇒ h = \(\frac{0.1272 \times 3.395}{0.8728}\) × 106
h = 0.495 × 106 m
h = 495 km
So, the satellite reaches a height of 495 km.
1st PUC Physics Gravitation One Mark Questions and Answers
Question 1.
What is acceleration due to gravity?
Answer:
The acceleration produced on a body falling freely under gravity is known as acceleration due to gravity.
Question 2.
Write the dimensional formula of G
Answer:
M-1L3T-2
![]()
Question 3.
What is the unit of G?
Answer:
Nm2kg-2
Question 4.
What are the factors affecting the value of G?
Answer:
It is a universal constant and is not affected by any factors.
Question 5.
Give the SI unit and dimensional formula of ‘g’.
Answer:
SI unit – m s-2, Dimensional formula LT-2
Question 6.
Write the expression for acceleration due to gravity at a height (altitude) ‘h’.
Answer:
The acceleration due to gravity at a height ‘h’ from the surface of earth is given by, g1= g \(\left[1-\frac{2 h}{R}\right]\) where g is the acceleration due to gravity on the surface of earth and R is the radius of the earth.
Question 7.
How does g vary with height above the surface of earth?
Answer:
g decreases with an increase in height.
Question 8.
Write the expression for acceleration due to gravity at a depth h below Earth’s surface.
Answer:
\(g^{\prime}=g\left[1-\frac{d}{R}\right]\), where g is the acceleration due to gravity and R is the radius of the Earth.
![]()
Question 9.
Where is the acceleration due to gravity on earth maximum?
Answer:
Acceleration due to gravity is maximum at the poles.
Question 10.
Where is acceleration due to gravity on earth minimum?
Answer:
Acceleration due to gravity is minimum at the equator.
Question 11.
What is the orbital velocity of a satellite?
Answer:
The velocity with which a satellite revolves in its closed orbit is called orbital velocity.
Question 12.
Write the expression for the orbital velocity of the satellite.
Answer:
The expression for orbital velocity of a satellite revolving round the earth in a closed orbit of radius ‘r’ is given by,
v = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}\)
where G is the gravitational constant and M is the mass of the earth.
Question 13.
What is the escape velocity of a body?
Answer:
The minimum velocity with which a body must be projected such that it escapes from the earth’s gravitational pull is called escape velocity.
Question 14.
Give the expression for the escape velocity.
Answer:
Escape velocity is given by,
Ve = \(\sqrt{\frac{2 G M}{R}}\)
where G is the gravitational constant, M is the mass of the earth and R is the radius of the earth.
![]()
Question 15.
What is a satellite?
Answer:
Satellite is an object moving round a planet in a closed and stable orbit.
Question 16.
What is a geostationary satellite?
Answer:
A satellite which revolves round the earth with the same angular speed and the same direction as that of earth around its axis is a geostationary satellite.
Question 17.
What is the period of a geostationary satellite?
Answer:
24 hours
Question 18.
What is meant by remote sensing?
Answer:
Obtaining data about a material from a distance using sensors is called remote sensing.
Question 19.
Mention the relation between escape velocity and Orbiting velocity.
Answer:
Escape velocity ve = \(\sqrt{2}\) vo
Question 20.
Assume a hole is made through the centre of the Earth along the diameter. What type of motion does the mass execute if it is dropped into the hole?
Answer:
Simple Harmonic Motion.
Question 21.
Is the potential energy of an object on the surface of Earth zero?
Answer:
No, It is given by \(-\frac{\mathrm{GM}}{\mathrm{R}}\).
Question 22.
What is basis for Kepler’s 2nd Law of Planetary Motion?
Answer:
The law of conservation of angular momentum.
![]()
Question 23.
If the Earth stops rotating axis. What will happen to the value of
Answer:
Since the Earth stopped rotation the centrifugal force pushing the objects outside becomes zero. So the value of g increases.
Question 24
Write one most important application of geostationary satellite.
Answer:
Long-distance communication.
Question 25.
What is the effect of Non-sphericity of Earth on the value of ‘g’?
Answer:
The value of g keeps varying with different places on Earth. It is maximum at poles and minimum at the equator.
Question 26.
What is the condition for a uniform sphere to be black hole?
Answer:
Condition is, \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\) = c,
Where M is mass of the sphere,
R is radius of sphere,
C is velocity of light.
Question 27.
How does the Orbital velocity of a satellite depends on the mass of the satellite?
Answer:
It is Independent of mass of satellite.
Question 28.
What does a spring balance measure mass or weight?
Answer:
Weight.
Question 29.
The Gravitational Potential Energy of a body at a point in a gravitational field of another body is \(-\frac{G M m}{r}\) What does -ve sign show?
Answer:
The negative sign implies that the body is bound to the body of mass M.
1st PUC Physics Gravitation Two Marks Questions and Answers
Question 1.
Define the potential energy of a body. Give an expression for the gravitational potential energy of a body.
Answer:
The energy possessed by a body due to its position is called potential energy. Gravitational potential energy is = mg h.
Question 2.
State and explain Newton’s law of gravitation.
Answer:
Everybody in this universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. If m1 and m2 are the masses of two bodies separated by a distance ‘r’, then the gravitational force F between them is,
\(\mathrm{F} \propto \frac{\mathrm{m}_{1} \mathrm{m}_{2}}{\mathrm{r}^{2}}\) or
\(\mathrm{F}=\frac{\mathrm{Gm}_{1} \mathrm{m}_{2}}{\mathrm{r}^{2}}\)
Where ‘G’ is.called the gravitational constant.
Question 3.
Define universal gravitational constant G. What is the dimensional formula of G?
Answer:
Gravitational constant is numerically equal to the force of attraction between two bodies of unit masses separated by unit distance.
Dimensional formula of G is [M-1L3 T-2]
Question 4.
Derive the relation between acceleration due to gravity (g) and the gravitational constant (G)
Answer:
Consider a body of mass ‘m’ on the surface of the earth of mass M. Let R be the radius of the Earth. The gravitational force exerted on the body according to Newton’s second law is,
F1 = mg ……(1)
where ‘g’ is acceleration due to gravity. According to Newton’s law of gravitation, the force between the body close to the surface of the earth and the earth is,
F2 = G. \(\frac{m M}{R^{2}}\) ………(2)
But F1 = F2
∴ mg = \(\frac{G m M}{R^{2}}\)
g = \(\frac{G M}{R^{2}}\).
![]()
Question 5.
Explain the variation of ‘g’ due to the shape of the earth?
Answer:
On the surface of the earth g = \(\frac{G M}{R^{2}}\)
Since G and M are constants g \(\propto \frac{1}{R^{2}}\)
Due to the ellipsoidal shape of the earth equatorial radius is greater than the polar radius. So ‘g’ is maximum at the poles than at the equator.
Question 6.
Mention the factors on which the orbital velocity and escape velocity depends.
Answer:
The orbital velocity and escape velocity depends on mass of the planet and its radius.
Question 7.
State and explain Kepler’s law for planetary motion.
Answer:
I Law :
Every planet moves in an elliptical orbit around the sun with sun at one of the focus.
II Law:
The line joining the planet to the sun sweeps out equal areas in equal interval of time.
III Law:
The square of the period of any planet about the sun is proportional to the cube of the semi-major axis of the ellipse.
Question 8.
Explain what is meant by weightlessness?
Answer:
The weight of a body is measured by the reaction of the surface which supports the body. When a person is standing on the lift the person the presses the surface with a force equal to his weight. The equal and opposite reaction of the surface on the person gives the sensation of weight.
When the lifts starts moving downwards with an acceleration, the reaction on the person becomes less and he feels his weight to be less.
When the lifts falls freely, both the person and the lift are moving downwards with equal acceleration. Thus the surface does not exert any force on the body. Such a state is called weightlessness. Similarly, the astronauts in a spacecraft orbiting round the earth experience weightlessness.
![]()
Question 9.
Give any two applications of remote sensing.
Answer:
- remote sensing is used for mapping of forests.
- remote sensing is used for groundwater exploration.
Question 10.
How is a satellite launched?
Answer:
In order to launch a satellite, it is taken vertically upwards to the required orbit and then appropriate horizontal velocity is imparted to the satellite so that it revolves round the earth.
Question 11.
Distinguish between inertial mass and gravitational mass.
Answer:
Inertial mass of a body is a measure of its inertia. It is determined using Newton’s second law of motion. Gravitational mass is a measure of the gravitational pull acting on it. It is determined using Newton’s law of gravitation.
Question 12.
Find the expression for the weight of the body at centre of the Earth.
Answer:
We know that, the value of acceleration due to gravity at depth d is given by \(\mathrm{g}_{\mathrm{d}}=\mathrm{g}\left[1-\frac{\mathrm{d}}{\mathrm{R}}\right]\) where R is radius of Earth.
At depth = R, gd = g[1 – R/R] = 0
So, weight of the body at centre of Earth is 0.
![]()
Question 13.
Is it possible to keep a satellite, so that it is always over Kashmir? Why?
Answer:
No, It is possible to place a geostationary satellite on an equatorial plane. Since Kashmir is not on the equator it is not possible to place a satellite above it.
Question 14.
Find the height at which g is the same as that at depth R/2.
Answer:
The acceleration due to- gravity at depth R/2 is
gd = g[1 – d/R] = g \(\left[1-\frac{\mathrm{R} / 2}{\mathrm{R}}\right]\)
= g/2
At height h

h = R/4
Question 15.
The mass of 2 bodies are tripled and distance is halved, how will the gravitational force change?
Answer:
We know that Fg = \(\frac{\mathrm{Gm}_{1} \mathrm{m}_{2}}{\mathrm{r}^{2}}\)
Now, m1 and m2 are made 3 m1 and 3 m2 respectively and r is made (r/2).
G (3m1)(3m2)
So, \(F_{g}^{\prime}=\frac{G\left(3 m_{1}\right)\left(3 m_{2}\right)}{(r / 2)^{2}}\) = 36 Fg
Gravitational force increases 36 times.
Question 16.
Define gravitational field strength. Find the field at a point distance ‘x’ form a mass ‘m1‘.
Answer:
The gravitational field is defined as the gravitation force experienced by an object of unit mass at any point. The Gravitational force on an object of mass m due to mass ‘m1‘ at a distance x.
F = \(\frac{\mathrm{Gm}_{1} \mathrm{m}}{\mathrm{x}^{2}}\)
Field = \(\frac{F}{m}=\frac{G m_{1}}{x^{2}}\)
Question 17.
A planet’s radius is reduced by 5%, with its mass unchanged. What is the percentage change in ‘g’?
Answer:
We know that g \(\propto \frac{1}{R^{2}}\)
So, \(\frac{\Delta g}{g}\) = – 2 \(\frac{\Delta R}{R}\)
⇒ \(\frac{\Delta g}{g}\) = – 2(5%) = – 10%
Question 18.
What is the gravitational force on a body inside a spherical shell? Why?
Answer:
Inside the shell, the net gravitational force is zero. This is because there is no mass inside, the gravitational field is zero, thereby force is zero.
Question 19.
The value of ‘g’ on the moon is 1/6th of that of Earth and diametre of moon is 1/4th that of Earth. Find the ratio of
escape velocities.
Answer:
We know that,

The escape velocity of moon is about 4.9 times that of Earth.
Question 20.
State universal law of gravitation. Establish the relation Me = \(\frac{\mathrm{g} \mathrm{R}_{\mathrm{e}}^{2}}{\mathrm{G}}\), where Me and Re are the mass and radius of Earth respectively.
Answer:
The universal law of gravitation states that everybody in the universe attracts every other body with a force which is directly proportional to their masses and inversely proportional to the square of distance between them.
F \(\propto \frac{m_{1} m_{2}}{r^{2}}\)
⇒ F = \(\frac{\mathrm{Gm}_{1} \mathrm{m}_{2}}{\mathrm{r}^{2}}\)
For the body of mass ‘m’ on earth.
F = mg = \(\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{m}}{\mathrm{R}_{\mathrm{e}}^{2}}\)
⇒ Me = \(\frac{R_{e}^{2} g}{G}\)
Question 21.
The radii of 2 planets are R and 2R respectively and their elements e and e/2 respectively. What is the ratio of their acceleration due to gravity at their surface?
Answer:
We know that,
g ∝ M and g ∝ 1/R2
⇒ g ∝ \(\frac{\rho \mathrm{V}}{\mathrm{R}^{2}}\) (∵ M = ρV)
Since V ∝ R3
g ∝ \(\frac{\rho \mathrm{R}^{3}}{\mathrm{R}^{2}}\)
i.e.; g ∝ ρR
Given that, ρ1 = ρ
ρ2 = ρ/2
R1 = R
R1 = 2R
⇒ \(\frac{\mathrm{g}_{1}}{\mathrm{g}_{2}}=\frac{\rho_{1} \mathrm{R}_{1}}{\rho_{2} \mathrm{R}_{2}}=\frac{\rho \mathrm{R}}{(\rho / 2)(2 \mathrm{R})}=1\).
![]()
Question 22.
The change In the value of ‘g’ at a height ‘h’ and depth ‘d’ is same. Assuming h and d are both very small compared to radius of Earth. Find ratio of h with respect to d.
Answer:
We know that ‘g’ at a height ‘h’ is given by \(g^{\prime}=g\left[1-\frac{2h}{R}\right]\) …….(1)
g at a depth ‘d’ is given by,
\(g^{\prime}=g\left[1-\frac{d}{R}\right]\) ……..(2)
Comparing (1) and (2), we can write
2h = d
⇒ \(\frac{h}{d}=\frac{1}{2}\)
Question 23.
If the Earth’s mass is 9 times and radius is 4 times that of Mars. Find the escape velocity of Mars. If that of Earth is 11.2 km s-1
Answer:
We know that, escape velocity is given by,
Vesc = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)
Let Vm, Ve be escape velocity of mars and Earth then, Vm = \(\sqrt{\frac{2 \mathrm{GM}_{\mathrm{m}}}{\mathrm{R}_{\mathrm{m}}}}\)
\(\sqrt{\frac{2 \mathrm{G}\left(\mathrm{M}_{\mathrm{e}} / 9\right)}{\left(\mathrm{R}_{\mathrm{e}} / 4\right)}}\)

= 7.47 kms-1
Question 24.
A black hole is a body from whose surface nothing may ever escape. What is the condition for a uniform spherical mass M to be a black hole? What should be radius of earth if it has to be a black hole?
Answer:
For a body to be a black hole, even light should not escape. So limiting escape velocity is 3 × 108 ms-1
So, for body of Mass M, condition is,
\(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\) ≥ 3 × 108 ms-1
For Earth, M = 6 × 1024 kg
\(\frac{2 \times 6.67 \times 10^{-11} \times 6 \times 10^{24}}{R}\) = (3 × 108)2 R
= 9 × 10-2 m
R = 9 cm.
1st PUC Physics Gravitation Three Marks Questions and Answers
Question 1.
The mass and diameter of a planet are 4 times those of Earth. What will be the time period of oscillation of the seconds pendulum on that planet?
Answer:
We know that the time period of oscillation of the pendulum is given by,
\(\mathrm{T}=\sqrt[2 \pi]{\frac{1}{g}}\)
Let the value of ‘g’ on the planet be gp and on earth be ge.
We know that, g ∝ \(\frac{M}{R^{2}}\)
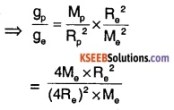

⇒ Tp = 2 Ts
Since it is a seconds pendulum Te = 1s
⇒ Tp = 2s.
Question 2.
Three equal masses are placed on three corners of equilateral triangles. What is work done in doing this?
Answer:
When ma is brought no work is done when mb is brought work done is, \(-\frac{G m_{a} m_{b}}{x}\)
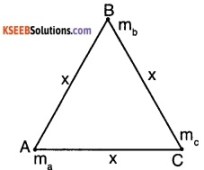
When mc is brought to point C from infinity.
The work done is \(-\frac{G m_{a} m_{c}}{x}\)\(-\frac{G m_{b} m_{c}}{x}\)
Total work done
![]()
Since all masses are equal, total work done is = \(-\frac{3 G m^{2}}{x}\)
Question 3.
Show that the gravitational potential at point of distant ‘a’ from the mass M1 is given by, V = \(-\frac{\mathrm{GM}_{1}}{\mathrm{a}}\).
Answer:
Consider a mass ‘m’ placed at a distance a from a mass M, then force is given by,
\(\mathrm{F}=\frac{\mathrm{GmM}_{1}}{\mathrm{a}^{2}}\)
Let the work done in moving the body through a distance dx, if it originally at a distance x, the work done be dw.
dw = F.dx

The potential energy is the amount of work done in bringing the object from ∞ to point ‘a’. PE, U = \(-\frac{\mathrm{GM}_{1} \mathrm{m}}{\mathrm{a}}\)
Gravitational potential is PE per unit mass
⇒ V = \(\frac{\mathrm{u}}{\mathrm{m}}=-\frac{\mathrm{GM}_{1}}{\mathrm{a}}\)
Question 4.
What happens to a body when it’s projected up with a velocity of 11.2 km s-1? Why? Compare escape speeds of 2 planets of mass M and 4 M and radii 2 R and R respectively.
Answer:
When the object is throw up with 11.2 km s-1, which is equal to the escape velocity. The object doesn’t come back and escapes from Earth’s gravitational field. The escape velocity is given by,
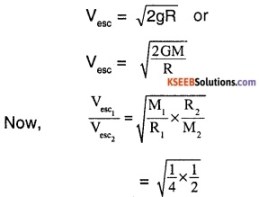
\(\frac{V_{\mathrm{esc}_{1}}}{V_{\mathrm{esc}_{2}}}=\frac{1}{2 \sqrt{2}}\)
The escape velocity of the 2nd planet is greater by a factor of 2\(\sqrt{2}\).
Question 5.
What are geostationary satellite? Calculate the height of the orbit above surface of Earth in which a satellite, if placed, will appear stationary.
Answer:
A geostationary satellite is a satellite which revolves around the Earth with exact same angular speed and direction as the Earth. Thus it appears stationary from Earth.
T = 24 × 3600 s = 8.64 × 104s
Let h be the height of orbit. Then,

≅ (4.24 × 107) – (6.4 × 106)m
≈ 3.6 × 107 m or 36,000 km from the surface of Earth.
Question 6.
Explain the variation of ‘g’ with
- height
- depth
Answer:
Consider M to be mass of Earth and R to be radius of Earth.
1. At a point ‘h’ above the ground
New g is gn = \(\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})^{2}}\)
\(=\frac{\mathrm{GM}}{\mathrm{R}^{2}\left[1+\frac{\mathrm{h}}{\mathrm{R}}\right]^{2}}\)
gn = g[1 + \(\frac{h}{R}\)]-2
if h << R,
gn = g[1 – \(\frac{2h}{R}\)]
So, g decreases with increase in height,
2. At a depth ‘d’ below the ground. The new g, gd is given by
dd = g[1 – \(\frac{d}{R}\)]
So, g also decreases with depth.
![]()
Question 7.
If the earth is one half of its present distance from the sun, How many days will the present one year on the surface will change?
Answer:
We know that, T2 ∝ R3
\(\left(\frac{T_{1}}{T_{2}}\right)^{2}=\left(\frac{R_{1}}{R_{2}}\right)^{3}\)
Since, R is halved
T1 = (1/2)3/2T
= \(\frac{T}{2 \sqrt{2}}\)
T1 = 129 days
The year of the new Earth will have 236 days lesser.
Question 8.
Define gravitational potential and field intensity. Give their units. Also, write relation between them.
Answer:
Gravitational potential at point is defined as the work done in bringing a body of unit mass from infinity to that point. Its unit is J/kg, denoted by V Gravitational field intensity is defined as the force experienced by a unit mass at that point. It is expressed in N/kg, denoted by I.
I = \(-\frac{\mathrm{V}}{\mathrm{R}}\)
Question 9.
A body weighs 90 kg f on the surface of Earth. What is its weight on a planet whose mass ln \(\frac{1}{9}\) and radius is \(\frac{1}{2}\) of Earth ?
Answer:
We know that g ∝ \(\frac{M}{R^{2}}\)

Let m be the mass of the object, then its weight is mgρ = m [\(\frac{4}{9}\) ge]
\(\frac{4}{9}\)(mgρ)
\(\frac{4}{9}\) (90kgf)
= 40kgf
Question 10.
The escape velocity v of a body depends on
- the acceleration due to gravity ‘g’ and
- the radius of planet ‘R’
Find the relation between them using dimension analysis.
Answer:
We know that,
Escape velocity = V = [LT-1]
Acceleration due to gravity = g = [LT-2]
and Radius = R = [L]
⇒ Let V = kgaRb
⇒ [LT-1] = [LaT-2a] [Lb]
a + b = 1 and -2a = -1
⇒ a = 1/2 and b =1/2
So, V = k \(\sqrt{\mathrm{Rg}}\).
![]()
Question 11.
State Newton’s Law of Gravitation. Find a % decrease in weight of the body when taken to a height of 16 km above surface of Earth. Radius of Earth a 6400 km.
Answer:
According to Newton’s Law of Gravitation, everybody in the universe attracts every other body with a force proportional to their masses and inversely proportional to the square of distance between them.
\(\mathrm{F} \propto \frac{\mathrm{m}_{1} \mathrm{m}_{2}}{\mathrm{r}^{2}}\)
⇒ F = \(\frac{\mathrm{Gm}_{1} \mathrm{m}^{2}}{\mathrm{r}^{2}}\), where
G → Universal Gravitational Constant
m1 and m2 → masses of the 2 bodies
r → distance between the bodies.
The % change is weight is given by
\(\frac{\Delta m g}{m g}\) × 100 = \(\frac{\Delta g}{ g}\) × 100 = \(\frac{\mathrm{g}-\mathrm{g}_{n}}{\mathrm{g}}\) × 100
We know that, gn = g \(g\left(1-\frac{2 h}{R}\right)\)

= 0.005
% change = \(\frac{\mathrm{g}-\mathrm{g}_{n}}{\mathrm{g}}\) × 100 = 0.5%
Question 12.
Define gravitational field strength. Which plane in the solar system has the greatest gravitational field strength? What is the gravitational field strength of a planet where a 60 kg astronaut weighs 300 N?
Answer:
The gravitational field strength at a point in a field is defined as the force experienced by a body of unit mass placed at that point.
I = \(\frac{G M}{R^{2}}\) ⇒ I = g
The value of I is maximum for Saturn.
I = \(\frac{300 N}{60 \mathrm{kg}}\)
I = 5 ms-2
1st PUC Physics Gravitation Five Marks Questions and Answers
Question 1.
What is a geostationary satellite? Write any four applications of artificial satellites.
Answer:
1 Part:
A satellite which revolves round the earth with the same angular speed and the same direction as that of earth around its axis is a geostationary satellite.
Uses of artificial satellites:
- for mapping of forests (or to study deforestation)
- for mapping of rivers, reservoirs
- for pollution monitoring.
- for weather forecasting, prediction, and warning of cyclones, mapping of flood-affected areas
- geostationary satellites are used for telephones, mobiles, broadcasting of radio and television.
Question 2.
What are orbital and escape velocity? Write relation between them. Mention any two characteristics of geostationary satellite.
Answer:
The velocity with which a satellite revolves in its closed orbit is called orbital velocity. The minimum velocity with which body must be projected so that it escapes form the gravitational force of attraction of earth is called escape velocity.
Escape velocity ve = \(\sqrt{2}\)Vo Where Vo is the orbital velocity.
Two properties of geostationary satellites:
- These satellites are appears to be stationary with respect to the earth’s surface.
- Their height form earth’s surface is about 36,000km and they revolve around the earth from west to east in the equatorial plane.
![]()
Question 3.
State and explain Newton’s Law of gravitation. Hence define universal gravitational constant and find the dimensional formula for it.
Answer:
The gravitational force of attraction between two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. If two masses m1 and m2 are separated by a distance r then \(\mathrm{F} \propto \frac{\mathrm{m}_{\mathrm{m}_{2}}}{\mathrm{r}^{2}}\) Or \(\mathrm{F}=\mathrm{G} \frac{\mathrm{m}_{\mathrm{1}} \mathrm{m}_{2}}{\mathrm{r}^{2}}\) Where G is the proportionality constant known as universal gravitational constant.
From the above equation, G = \(\frac{\mathrm{Fr}^{2}}{\mathrm{m}_{1} \mathrm{m}_{2}}\)
If m1 = m2 = 1 and r = 1 then G = \(=\frac{F(1)^{2}}{1 \times 1}\) = F
Gravitational constant is defined as the gravitational force attraction between two bodies of unit masses separated by unit distance. Dimensional formula for [G] = [M-1 L3 T-2 ].
Question 4.
What is the difference between gravitational potential energy and gravitation potential? Derive an expression for gravitational potential energy.
Answer:
The gravitational potential is the gravitational potential energy per unit mass. So it is independent of the mass considered. The gravitational potential energy is defined as the work done in bringing a mass ‘m’ from infinity to the given point.
We know that, F = \(\frac{\mathrm{GMm}}{\mathrm{x}^{2}}\), where x is the distance between M and m.
Work done in moving the mass by dx from

The gravitational potential V= \(\frac{\mathrm{U}}{\mathrm{m}}\)
= \(-\frac{\mathrm{GM}}{\mathrm{r}}\)
Question 5.
Define the term orbital velocity. Establish a relation for the orbital velocity of a satellite very close to the surface of the earth. Find the ratio of orbital velocity and escape velocity.
Answer:
Orbital velocity is the minimum velocity that is needed to put the satellite into a given orbit around Earth. Consider a satellite of mass ‘m’ moving around in an orbit at height ‘h’ above the ground. Let M be mass of Earth, R be the radius of earth and the orbital velocity be Vo.
We know that, Fg = \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^{2}}\)
and centrifugal force FC = \(\frac{m V_{0}^{2}}{(R+h)}\)
In equilibrium i.e., while rotating around the orbit

(Since, h << R ; R + h = R)
\(\frac{V_{0}}{V_{e s c}}=\frac{\sqrt{g R}}{\sqrt{2 g R}}=\frac{1}{\sqrt{2}}\)
Question 6.
Obtain an expression for escape velocity of an object of mass ‘m’ from the surface of planet of mass M and radius R. If the escape velocity of planet is know to be 11.2 km s-1. How fast will the object move If its velocity of launch is 22.4 km s-1 from the surface?
Answer:
The minimum velocity required to escape from the gravitational force of the planet is known as the escape velocity of the planet. Consider the object ‘m’ on the surface of Earth.
Initial PE = \(-\frac{\mathrm{GMm}}{\mathrm{R}}\)
Initial KE = \(\frac{1}{2} m\left(V_{\text {esc }}\right)^{2}\)
Total energy = \(\frac{1}{2} m\left(V_{\text {esc }}\right)^{2}-\frac{G M m}{R}\)
To escape, the KE should greater than or equal to its PE.
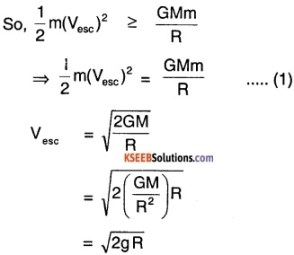
Initial velocity of object = 22.4 km s-1
= 2 Vesc
Total Initial Energy
= \(\frac{1}{2}\) m(2Vesc)2 – \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
= 2 m \(V_{\text {esc }}^{2}\) – \(\frac{1}{2}\) m \(V_{\text {esc }}^{2}\) [From(1)]
= \(\frac{3}{2}\) m \(V_{\text {esc }}^{2}\) ……(2)
Total Final energy = PE (at ∞) + \(\frac{1}{2}\) mVf2
= 0+ \(\frac{1}{2}\) mVf2
= \(\frac{1}{2}\) mVf2 ………(3)
By conservation of energy, (2) = (3)
Vf = \(\sqrt{3}\) Vesc
= 19.4 km s-1
1st PUC Physics Gravitation Numerical Problems Questions and Answers
Question 1.
Find the gravitational force between two masses 15 kg each separated by a distance of 2m.
(G = 6.67 × 10-11Nm2kg-2)
Solution:
Given, m1 = m2 = 15 kg
d = 2 m
G = 6.67 × 10-11Nm2kg-2
∴ F = \(\frac{m_{1} m_{2}}{d^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 15 \times 15}{2^{2}}\)
= 3.75 × 10-9 N.
Question 2.
Find the height at which the acceleration due to gravity is 1% less than its value on the surface of the earth. Radius of the earth 6400 km.
Solution:
Let h be the height where the acceleration due to gravity is 1 % less than that on the surface of the earth. Then,
\(g^{\prime}=g\left(1-\frac{2 h}{R}\right)\)
Here, g’ = 1 % less than g.

= 32 km.
Question 3.
The mass of a sphere is twice the mass of another sphere. These spheres attract each other with a force of 2 × 10-4 N. When they are moved 0.3 m apart, the force reduces to 5 × 10-5N. Find
- the mass of the spheres.
- Initial separation between the spheres.
Solution:
Let m be the mass of one sphere. Then the mass of second sphere is 2 m. If ‘d’ is the initial separation between the two spheres,
F1 = \(\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{m}_{2}}{\mathrm{d}^{2}}\)
= G \(\frac{\mathrm{m} \times 2 \mathrm{m}}{\mathrm{d}^{2}}\) ……(1)
When they are moved 0.3 m further apart,
F2 = G \(\frac{\mathrm{m} \times 2 \mathrm{m}}{(\mathrm{d}+0.3)^{2}}\) ………(2)
Dividing (1) by (2),

Taking square root,
2 = \(\frac{(\mathrm{d} + 0.3)}{\mathrm{d}}\) or d = 0. 3 m
∴ Initial separation between the spheres is 0. 3 m
To find the mass, substituting in equation (1)

∴ m = 367.3 kg
2m = 734.61 kg
Question 4.
Calculate the height at which the acceleration due to gravity becomes\(\left(\frac{1}{16}\right)^{t h}\) of its value on the surface.(Radius of the earth 6400 km).
Solution:
Acceleration due to gravity at a height h is given by,

\(\frac{h}{R}\) = 3
h = 3R = 3 × 6400
= 19,200 km.
Question 5.
An artificial satellite revolves in a circular orbit at height 600 km above the earths surface. What is the orbital velocity and period of revolution of the satellite? ( Radius of the earth = 8400 km, g = 9.8 ms-2)
Solution:
Orbital velocity is given by,
v = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}\)
where G is the gravitational constant, M is the mass of the earth.
We have, g = \(\frac{G M}{R^{2}}\) and GM = gR2
v = \(\sqrt{\frac{\mathrm{gR}^{2}}{\mathrm{r}}}\)
\(=\sqrt{\frac{g R^{2}}{R+h}}\)
where ‘h‘ is the height of the satellite above the earth’s surface.
∴ v = \(\sqrt{\frac{9.8 \times\left(6400 \times 10^{3}\right)^{2}}{6400 \times 10^{3}+600 \times 10^{3}}}\)
= 7.57 × 103 ms-1
Period of revolution, T = \(\frac{2 \pi r}{v}\)

= 5810 seconds
Question 6.
The acceleration due to gravity on moon is 1.7 ms-2 and its radius is 0.27 times the radius of the earth. Calculate the ratio of mass of the earth to the mass of the moon. The acceleration due to gravity on the earths surface is 9.8 ms-2
Solution:
Acceleration due to gravity on moon, gm = 1.7 ms-2
Acceleration due to gravity on earths surface gE = 9.8 ms-2
Given, Rm = 0.27 RE where Rm and RE are the radii of moon and the earth respectively. Acceleration due to gravity on moon is
gm = \(\frac{\mathrm{GM}_{\mathrm{m}}}{\mathrm{R}_{\mathrm{m}}^{2}}\) …..(1)
Acceleration due to gravity on earth is
gE = \(\frac{\mathrm{GM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}^{2}}\) ……(2)
where Mm and ME are the masses of moon and earth respectively.

= 79
Mass of the earth is 79 times the mass of the moon.
Question 7.
A Saturn year is 30 times the earth year. How far is the Saturn from the sun if the earth is 1.50 × 108 km away from the sun?
Solution:
According to Kepler’s third law, T2 ∝ R3
∴\(\frac{\mathrm{T}_{\mathrm{S}}^{2}}{\mathrm{T}_{\mathrm{E}}^{2}}=\left(\frac{\mathrm{R}_{\mathrm{S}}}{\mathrm{R}_{\mathrm{E}}}\right)^{3}\) …..(1)
where TS and TE are the period of revolution of Saturn and the earth and RS and RE are the distances of Saturn and the earth from the sun respectively.
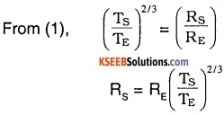
Given RE = 1.50 × 1011m
TS = 30 × TE
∴ RS = 1.50 × 1011 × \(\left(\frac{30 T_{E}}{T_{E}}\right)^{2 / 3}\)
= 1.50 × 1011 x 302/3
= 1.448 × 1012 m
= 1.448 × 109 km.
Question 8.
Determine the escape velocity of a body from the moon assuming moon to be a uniform sphere of radius 1.74 × 106m and mass 7.36 × 1022kg. Based on the answer explain why moon has no atmosphere.
(G = 6.67 × 10-11 Nm2kg-2).
Solution:
Escape velocity is given by,

= 2.38 × 103 ms-1
= 2.38 km s-1
The escape velocity from the moon is 2.38kms-1 which is less than the r.m.s. value of velocity of gas molecule. Hence all gases which might have been on the surface of the moon had escaped from moon. Hence moon has no atmosphere.
Question 9.
Mass of Jupiter is 320 times that of earth and its radius is 11 times the earth’s radius. Calculate the escape velocity of a body from Jupiter’s surface, given that escape velocity of earth’s surface is 11.2 km s-1
Solution:
The escape velocity from Jupiter’s surface is given by,
VJ = \(\sqrt{\frac{2 \mathrm{GM}_{\mathrm{J}}}{\mathrm{R}_{\mathrm{J}}}}\)
where MJ and RJ are the mass and radius of Jupiter respectively.
Given that, MJ = 320 ME and RJ = 11 RE

= \(\sqrt{\frac{320}{11}}\) × 11.2 × 103
= 5.394 × 11.2 × 103 ms-1
= 60.41 kms-1.
![]()
Question 10.
Determine the angular velocity with which earth would rotate on its axis so that a person on the equator would weigh 3/5 of his present weight. Radius of earth = 6400 km, g = 9.8 ms-2
Solution:
Real weight of the person W = mg
Apparent weight of the person due to the rotation of the earth,
W’ = mg’
But W’ = \(\frac{3}{5}\)W
mg’ = \(\frac{3}{5}\) mg or
g’ = \(\frac{3}{5}\) g
Variation of acceleration due to gravity on the equator is given by,
g’ = g – ω2R
i.e. \(\frac{3}{5}\) g = g – ω2R
∴ ω2R = \(\frac{2}{5}\) g
ω = \(\sqrt{\frac{2 g}{5 R}}\)
\(=\sqrt{\frac{2 \times 9.8}{5 \times 6400 \times 10^{3}}}\)
= 7.8 × 10-4 rads-1.
Question 11.
A satellite circling round the earth has a period of 10 hours. Calculate its height above the surface of the earth., g = 9.8ms-2
Solution:
Period of revolution of the satellite, T = 10hrs
= 10 × 60 × 60 = 36,000 sec
g = 9.8ms-2.
From, the equation

R = 321.6 × 106m
orbital velocity vo = \(\sqrt{\mathrm{gR}}\)
\(=\sqrt{9.8 \times 321.6 \times 10^{6}}\)
= 56.14 × 103ms-1
∴ from the equation T = \(\frac{2 \pi(\mathrm{R}+\mathrm{h})}{\mathrm{v}_{0}}\)
3600 = \(\frac{2 \times 3.142\left(321.6 \times 10^{6}+h\right)}{56.14 \times 10^{3}}\)
2021040 = 2020.9 × 106 + 6.284h
h = \(\frac{0.14 \times 10^{6}}{6.284}\)
= 222.79km.
Question 12.
Calculate the acceleration due to gravity
- at a height 16km above Earth’s surface and
- at a depth 2.8km below the surface of the earth. (Radius of the earth is 6400 km and acceleration due to gravity on the surface of the earth = 9.8m/s-2).
Solution:
1. Acceleration due to gravity,
g=9.8ms-2, Height h = 16 × 103m Radius of the earth, R = 6400 × 103 m From the equation g1 = g \(\left(\frac{\mathrm{R}}{\mathrm{R}+\mathrm{h}}\right)^{2}\)
= 9.8 \(\left(\frac{6400 \times 10^{3}}{6400 \times 10^{3}+16 \times 10^{3}}\right)^{2}\)
= 9.75 ms-2
2. depth, h = 2.8 × 103m
From the equation g1 = g \(\left[1-\frac{h}{R}\right]\)
= 9.8 \(\left[1-\frac{2.8 \times 10^{3}}{6400 \times 10^{3}}\right]\)
= 9.796 ms-2
![]()
Question 13.
The gravitational force between two bodies. A and B is 6.4 × 10-7 N. When the distance between them is decreased by 0.2m. the force increases to 14.4 × 10-7 N. Find their original distance apart. If the mass of A is twice that of B, find the mass of A and B. Given G = 6.67 × 10-11Nm2kg-2
Solution:
1. Let the mass of body A = m1
Let the mass of body B = m2
Let ‘ α ’ be the distance
force F = 6.4 × 10-7N
F = \(\frac{\mathrm{G} \mathrm{m}_{1} \mathrm{m}_{2}}{\mathrm{d}^{2}}\)
6.4 × 10-7 = \(\frac{\mathrm{G} \mathrm{m}_{1} \mathrm{m}_{2}}{\mathrm{d}^{2}}\) (1)
2. Now the distance, d = d – 0.2 force, F= 14.4 × 10-7N
14.4 × 10-7 = \(\frac{\mathrm{G}_{\mathrm{m}_{1} \mathrm{m}_{2}}}{(\mathrm{d}-0.2)^{2}}\) (2)
![]()
Taking Square root on both sides we have 1.5 = \(\frac{d}{d-0.2}\)
d = 1.5d – 0.3
d = 0.6m
3. If the mass, of A is twice that of B then m1 = 2m2, force F = 14.4 × 10-7N
∴ 14.4 × 10-7 = \(\frac{6.67 \times 10^{-11} \times 2 m_{2} \cdot m_{2}}{0.6}\)
m22 = 0.6477 × 104
m2 = 0.8048 × 102kg = 80.48kg
m1 = 2m2 = 1.61 × 102kg
= 161kg.
Question 14.
The mass and diameter of a planet are 3 times that of the earth, what is the acceleration due to gravity on the surface of planet (given ‘g’ on the surface of earth is 9.8m/s2).
Solution:
Mass of the planet M1 = 3Mearth
Diameter of the planet, R1 = 3Rearth
Let g1 be the acceleration due to gravity on the surface of the earth whose mass Mearth & Radius Rearth Then,
g = \(\frac{\mathrm{GM}_{\mathrm{earth}}}{\mathrm{R}_{\mathrm{earth}}^{2}}\) (1)
Let g1 be the accleration due to grav-ity. on the surface of the planet whose mass is M1 & Radius is R1 then
g1 = \(\frac{\mathrm{GM}^{1}}{\left(\mathrm{R}^{1}\right)^{2}}\)
g1 = \(\frac{\text { G3M earth }}{3 \mathrm{R} \text { earth }}=\frac{\text { GMearth }}{3 \mathrm{R}_{\text {earth }}^{2}}\) (2)
Divide equ (2) by equ (1)

= 3.267 m s-2
Question 15.
An artificial satellite revolves round the earth at a height of 1200km, the radius of the earth is 6400km. What is its orbital velocity and time period of revolution?
Answer:
Orbital velocity, vo = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}\)
But we have, g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) ⇒ GM = gR2
∴ vo = \(\sqrt{\frac{9 R^{2}}{r}}=\sqrt{\frac{g R^{2}}{R+h}}\)
where ‘h’ is the height of the satellite above the earths surface.
∴ vo = \(\sqrt{\frac{9.8 \times\left(6400 \times 10^{3}\right)^{2}}{6400 \times 10^{3}+1200 \times 10^{3}}}\)
= 7.27 x 103ms-1
Period of revolution, T = \(\frac{2 \pi r}{v_{0}}\)

= 6569 seconds
Question 16.
Calculate the mass and density of the earth from the following data. Gravitational constant = 6.67 × 10-11Nm2Kg-2 Radius of the earth = 6.4 × 106m. Acceleration due to gravity = 9.8ms-2.
Answer:
G = 6.67 × 10-11Nm2<Kg-2,
R = 6.4 × 106m , g = 9.8 m/s-2, M = ? and ρ =?
g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) or M = \(\frac{\mathrm{g} \mathrm{R}^{2}}{\mathrm{G}}\)
= \(\frac{9.8 \times\left(6.4 \times 10^{6}\right)^{2}}{6.67 \times 10^{-11}}\)
= 60.18 × 1023kg
= 6 × 1024 kg.
Density
ρ = \(\frac{3 g}{4 \pi R G}\)
= \(\frac{3 \times 9.8}{4 \times 3.14 \times 6.4 \times 10^{6} \times 6.67 \times 10^{-11}}\)
= 5.483 × 103 kg/m3.
Question 17.
A person can jump 1.2 m on Earth. How high can he jump on a planet whose density is 1/3rd and radius is 4 times that of Earth, assuming he uses same energy.
Answer:
We know that,
g ∝ \(\frac{M}{R^{2}}\)

Now, since same energy is spent
mgphp = mgehe
⇒ hp = \(\left(\frac{g_{e}}{g_{p}}\right)\) he
\(\frac{3}{4}\) × 1.2m
hp = 0.9m.
Question 18.
Find ratio of the accelerations due to gravity of 2 planets if their radii ratio is 2 : 3. Under condition
- Mass remains constant
- Material remains constant.
Answer:
1. Here since mass remains constant, g ∝ \(\frac{M}{R^{2}}\) ⇒ g ∝ 1/R2
⇒ Ratio of gravitation is,
\(\frac{g_{1}}{g_{2}}=\left(\frac{R_{2}}{R_{1}}\right)^{2}=\frac{9}{4}\)
2. Here since material is same its density is same ⇒ g ∝ ρR ⇒ g ∝ R
∴ \(\frac{g_{1}}{g_{2}}=\left(\frac{R_{1}}{R_{2}}\right)=\frac{2}{3}\)
Question 19.
Find the percentage change in velocity of moon to escape the Earth’s gravity.
Answer:
Initial Velocity of moon = Orbital
Velocity, Vo = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}\)
For the moon to escape Earth’s influence,
its velocity must become \(\sqrt{2 \frac{\mathrm{GM}}{\mathrm{r}}}\)
So, increase in velocity required

Percentage change
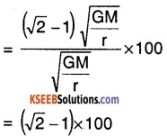
= 41.4 %
Question 20.
A rocket is launched with 0.8 times escape velocity. How high will it go before it starts falling?
Answer:
Initial KE = \(\frac{1}{2}\) mVr2
\(\frac{1}{2}\) m (0.8)2 (Vesc)2
= (0.64) [\(\frac{1}{2}\) m \(V_{\text {esc }}^{2}\)]
= 0.64 \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Initial PE = \(-\frac{\mathrm{GMm}}{\mathrm{R}}\)
At the height ‘h’, its velocity is 0.
So Final Potential Energy = \(-\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}\)
By Law of Conservation of Energy
(0.64)\(\frac{\mathrm{GMm}}{\mathrm{R}}-\frac{\mathrm{GMm}}{\mathrm{R}}=\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}\)
0.36(R + h) = R
h = \(\frac{0.64}{0.36}\) R = \(\frac{16}{9}\) R
So, the rocket reaches a height of \(\frac{16}{9}\) R,
where R is radius of the Earth.
![]()
Question 21.
A mass m is left to fall freely to fall from a height R/3 from the surface of Earth. What is Its velocity when it hits the surface of Earth.
Answer:
Initial KE = 0,
Initial PE = \(\frac{-G M m}{(R+R / 3)}\) = \(-\frac{3}{4} \frac{\mathrm{GMm}}{\mathrm{R}}\)
Total Energy = \(-\frac{3}{4} \frac{\mathrm{GMm}}{\mathrm{R}}\) …..(1)
at the surface of the Earth, let its velocity be Vf then
TE = \(\frac{1}{2}\) m(Vf)2 – \(\frac{\mathrm{GMm}}{\mathrm{R}}\) ….(2)
By conservation of energy (1) = (2)

\(\frac{1}{2}\) Vesc
= 5.6 km s-1
Question 22.
Calculate the increase in potential energy when a body is moved from the surface of Earth to a height 2 R from the surface, where R is the radius of Earth.
Answer:
The Potential Energy of object on the surface of Earth is U l = \(-\frac{\mathrm{GMm}}{\mathrm{R}}\)
The Potential Energy at the height of 2 R from surface is Uf = \(-\frac{G M m}{(R+2 R)}\)
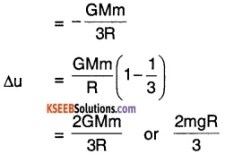
Question 23.
Show that velocity of a body released from a height r from centre of Earth (r > R) is
R [2g \(\left(\frac{1}{\mathbf{R}}-\frac{1}{\mathbf{r}}\right)\)]1/2 when it reaches the Earth’s surface is, where R is radius of Earth.
Answer:
From law of conservation of Energy we can write \(-\frac{\mathrm{GMm}}{\mathrm{r}}=\frac{1}{2} \mathrm{mV}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}}\)

V = \(\mathrm{R}\left(2 \mathrm{g}\left(\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{r}}\right)\right)^{1 / 2}\)
Question 24.
Determine the speed with which the Earth has to rotate so that the weight of a person on the equator is 2/3rd of the current weight. Assume radius of Earth is 6.4 × 106 m.
Answer:
Let m be the mass of the person, then,
Original weight = mg
and new weight = mg’
Given that \(\frac{\mathrm{mg}^{\prime}}{\mathrm{mg}}=\frac{2}{3}\)
⇒ g’ = \(\frac{2}{3}\) g
We know that,
g’ = g – Rω2 (for equatorial plane)
\(\frac{2}{3}\) g = g – Rω2
⇒ ω = \(\sqrt{\frac{\mathrm{g}}{3 \mathrm{R}}}\)
ω = \(\sqrt{\frac{9.8}{3 \times 6.4 \times 10^{6}}}\)
ω = 5.104 × 10-4rad s10-1.
Question 25.
Two stars of mass Mx and My of radii Rx and Ry are d distance apart. Now if there is a particle of mass m at the midway, find the minimum speed with which it needs to be projected to escape to infinity.
Answer:
The initial potential energy of the mass is, given by
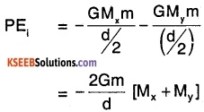
Let the initial velocity be Vi
then KEi = \(\frac{1}{2}\) m(Vi)2
So, Total Energy
\(\frac{1}{2}\) mVi2 – \(\frac{2 G m}{d}\) (Mx + My)
Total Final Energy = 0
By conservation of Energy,

Question 26.
The mass of Jupiter is 1.9 × 1027 kg and that of Sun is 2 × 1030kg. The mean distance between them is 7.8 × 1011m. Find the gravitational force exerted by Sun. Also, calculate the speed of Jupiter assuming circular orbit around the Sun.
Answer:
Mass of Jupiter = 1.9 × 1027kg
Mass of Sun = 2 × 1030kg
Distance, r = 7.8 × 1011m
So, gravitational Force, Fg = \(-\frac{G M_{1} M_{2}}{r^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 1.9 \times 2 \times 10^{57}}{(7.8)^{2} \times 10^{22}}\)
= 4.16 × 1023N
Now, the Fg is equal the centrifugal force of Jupiter.
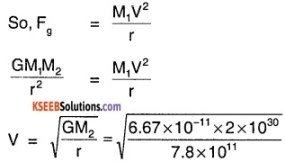
= 1.3 × 104 m s-1 or 13 km s-1.
Question 27.
A 500 kg satellite is in a circular orbit of radius 2 RE about the Earth. How much energy is required to move it to another orbit of radius 4 Re? What are changes in kinetic and potential energies?
Answer:
Mass of satellite, ms = 500 kg
Let ME be mass of Earth and RE be radius of earth.
The PE1 = \(-\frac{G M_{E} m_{s}}{2 R_{E}}\)
and KE1 = \(\frac{1}{2}\) mvo2 = \(\frac{1}{2}\) ms \(\left(\frac{\mathrm{GM}_{\mathrm{E}}}{2 \mathrm{R}_{\mathrm{E}}}\right)\)
= \(\frac{\mathrm{GM}_{\mathrm{E}} \mathrm{m}_{\mathrm{s}}}{4 \mathrm{R}_{\mathrm{E}}}\)
Total Energy, TE1

Similarly for new orbit
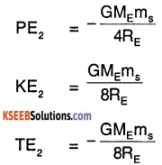
Difference in Energy = TE2 – TE1

= 3.92 × 109 J
An energy of 3.92 GJ needs to be supplied to the satellite to change its orbit.
Change in PE = \(\frac{G M_{E} m_{s}}{2 R_{E}}-\frac{G M_{E} m_{s}}{4 R_{E}}\)
= \(\frac{\mathrm{GM}_{\mathrm{E}} \mathrm{m}_{\mathrm{s}}}{4 \mathrm{R}_{\mathrm{E}}}\)
= 2 × 3.92 × 109 J
= 7.84 × 109 J
Change in KE = \(\frac{G M_{E} m_{s}}{8 R_{E}}-\frac{G M_{E} m_{s}}{4 R_{E}}\)
= – 3.92 × 109 J.
![]()
Question 28.
A solid sphere of R/2 is cut and removed as shown. If ρ is the density of material. A mass ‘m’ is place at a distance R from centre of sphere. Find the gravitational force of attraction the mass.
Answer:
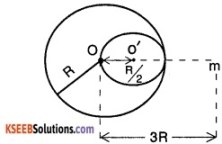
Mass of the Sphere is,
M1 = ρ × \(\frac{4}{3}\)R3
Force due to the sphere.
F1 = \(\frac{\mathrm{GM}_{1} \mathrm{m}}{(3 \mathrm{R})^{2}}\)
The Mass of missing portion
M2 = ρ \(\frac{4}{3}\) π (R/2)3 = ρ × \(\frac{4}{3}\) × \(\frac{\pi \mathrm{R}^{3}}{8}\)
= \(\frac{M_{1}}{8}\)
Force on mass from only the missing portion
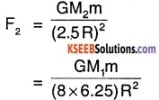
The total effective force on the mass is, F = F1 – F2

= 0.38 × G × R × ρ × m.
Question 29.
Infinite number of masses are placed at x = 1, 2, 4, 8….. If each of these masses are equal to ‘m’. Find the potential energy on a mass ‘m’ at origin.
Answer:
The gravitational potential energy at a point distance x from a mass m is given
by \(-\frac{\mathrm{Gmm}}{\mathrm{x}}\)
The total potential energy is given by,

[sum of infinity GP]
= – 2Gm2
Question 30.
Two masses m1 and m2 are separated by a distance r. Find the expression for gravitational potential at a point where the net force is zero.
Answer:
Let x be the distance of the point where net force is zero from m.
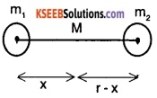
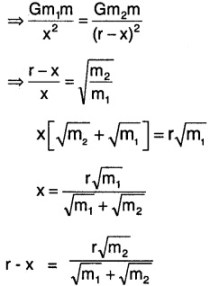
The potential at the point x is
