You can Download Chapter 7 System of Particles and Rotational Motion Questions and Answers, Notes, 1st PUC Physics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Physics Question Bank Chapter 7 System of Particles and Rotational Motion
1st PUC Physics System of Particles and Rotational Motion TextBook Questions and Answers
Question 1.
Give the location of the centre of mass of a
- sphere,
- cylinder,
- ring, and
- cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
Answer:
The Centre of mass of sphere cylinder, ring and cube with homogenous mass distribution lies at its geometric centre. It is not necessary that CM (centre of mass) lies inside the body as in the cases of ring or hollow hemisphere.
Question 2.
In the HCL molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10-10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
Answer:
Let nucleus of hydrogen atom be at the origin and nucleus of chlorine lie on x-axis. If the CM of the HCI system lie at (Xcm, 0), then
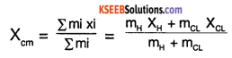
given, mCL = 35.5 mH
![]()
= \(\frac{35.5}{36.5}\) × 1.27 Å = 1.235 Å
Question 3.
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
Answer:
There is no external force acting on the child and the trolley system, hence the momentum of the entire system is conserved. Therefore the CM keeps moving with its initial speed of V in the same direction.
![]()
Question 4.
Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b.
Answer:
Consider two vectors a and b with an internal angle ‘θ’ between them.
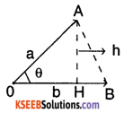
The area of the triangle OAB formed by the vectors a, b is
A = \(\frac{1}{2}\) × OB × AH

The magnitude of the vector product a × b is ![]()
∴ Area of the triangle = \(\frac{1}{2}\) × \(|\mathrm{a} \times \mathrm{b}|\)
Question 5.
Find the components along the x, y, z axes of the angular momentum I of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and pz. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
Answer:

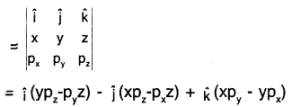
∴ Lx = ypz – zpy, Ly = zpx – xpz and
Ly = xpy – ypx
If the particle moves only in the x – y plane, then z = 0 and pz = 0
⇒ Lx = y(0) – (0)py = 0
Ly = (0) (px) – x (0) = 0
Lz = xpy – ypx; L= Lz\(\hat{K}\)
Question 6.
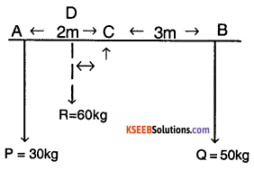
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig.7.39. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
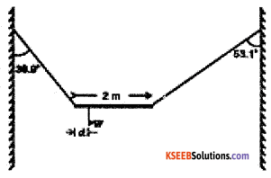
Answer:
Consider the free body diagram (BD) of rod and system.
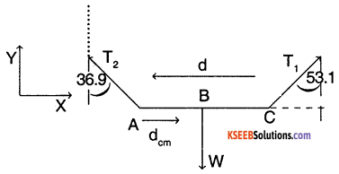
The system is both in rotational and translational equilibrium.
∴ Σ Fextrernal = 0
Σ \(\bar{\tau}_{\text {external }}\) = 0
Σ Fx = T1 sin (53.1) – T2 sin (36.9°) = 0 (1)
Σ Fy = T1 cos (53.1) + T2 cos (36.9) – w = 0 ………….. (2)
Σ \(\vec{\tau}_{z}\)(about A)
= T1 cos (53.1) (d) – W(dcm) = 0 ……….. (3)
(1) ⇒ T1 = T2 \(\frac{\sin (36.9)}{\sin (53.1)}\) = \(\frac{(3 / 5)}{(4 / 5)}\)T2 = (0.75) T2
⇒ T2 = \(\frac{4}{3}\) T1 ………. (4)
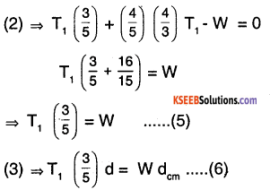
From (5) and (6)
\(\frac{T_{1}(3 / 5) d}{T_{1}(5 / 3)}\) = dcm
∴ dcm = \(\left(\frac{9}{25}\right)\) d = \(\frac{9}{25}\) × 2m = 0.72m
Question 7.
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
Answer:
Consider the free body diagram (FBD) of the car with all the forces
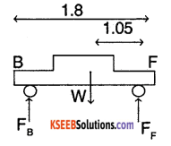
The car is in rotational equilibrium
∴ Σ τ (around any stationery point) = 0
Also w = mg = (1800) × (9.8) …………. (1)
consider the torque around F and B
Σ \(\bar{\tau}\) (about F) = W (1.05) – FB (1.8) = 0
where FB is the force on the back wheels.
From the above equation,
FB = \(\frac{m g(1.05)}{(1.8)}\) = 10290 N
similarly ΣF (about B) = 0
⇒ W (1.8 – 1.05) = FF (1.8)
∴ Force on front wheels,
FF = \(\frac{m g(0.75)}{(1.8)}\) = 7350 N
Total force exerted by ground
= FF + FB = 7350 + 10290
=17640 N
Question 8.
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR²/4, where M is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be 2MR²/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Answer:
(a) Moment of inertia of sphere about its diameter = \(\frac{2}{5}\)MR²
Using Parallel axes theorem, Moment of inertia of this sphere about any tangent to the sphere is = 1CM + Md²
= \(\frac{2}{5}\)MR² + MR²
= \(\frac{7}{5}\)MR²
(b) Moment of inertia of the of disc about its diameter = \(\frac{\mathrm{MR}^{2}}{4}\)
\(\left.\right|_{\mathrm{AB}}\) = MR²/4
1AB = \(\frac{M R^{2}}{4}\)
Using the perpendicular axes theorem for planar objects,
1PQ = 21AB = MR²/2
using parallel axes theorem,
![]()
= MR²/2 + MR² = \(\frac{3}{2}\)MR²
Question 9.
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Answer:
M.I. of sphere about its axis = \(\frac{2}{5}\) MR²
M.1. of hollow cylinder about its axis = MR²
Since torque to both bodies are the same
τ = 1 α ⇒ α = \(\frac{\tau}{1}\)
Hence the object with lesser M.1. will have a higher angular acceleration and hence higher angular speeds at any moment. Thus the sphere will have higher angular speeds after a given time.
![]()
Question 10.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s-1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
Answer:
Given M = 20 kg , ω = 100 rad/sec and R = 0.25m
Kinetic energy (Rotation) = \(\frac{1}{2}\) l × ω²

= 3.125 KJ
L (angular momentum) = I ω = \(\frac{\mathrm{MR}^{2}}{2}\) × ω
= \(\frac{20(0.25)^{2}}{2}\) × 100 = 62.5 Js.
Question 11.
(a) A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
Answer:
(a) initial angular speed,
ωo =40 rev/min
Initial M.I. = Io
Final M.I. = 2/5 Io
Since the turntable rotates without friction, there is no external torque being applied to the child turntable system. Hence angular momentum in conserved
∴ ω0 I0 = If ωf = 2/5I0 (ωf )
∴ ωf (final angular speed) = \(\frac{5 \omega_{0}}{2}\)
= \(\frac{5}{2}\) × 40 rev/min
= 100 rev/min
= 100 rpm.
(b) Initial kinetic energy is given by,
K1 = \(\frac{1}{2}\) I0 ω²0
Final Kinetic energy K2 = \(\frac{1}{2}\) I0 ω²f

Hence there is a 150% increase in the kinetic energy of the system. The child uses its internal energy to increase its Kinetic energy.
Question 12.
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
Answer:
The only external force being applied on the cylinder is that of 30 N
∴ Fext = 30N = m aCM where aCM is the linear acceleration of the centre of mass.
∴ aCM = \(\frac{30}{3}\) = 10 m/sec²
Angular acceleration αCM = \(\frac{\tau}{l}\) = \(\frac{30 \times r}{m r^{2}}\)
= \(\frac{30}{m r}=\frac{30}{3 \times(0.4)}\) = 25 rad/sec²
Question 13.
To maintain a rotor at a uniform angular speed of 200 rad s-1, an engine needs to transmit a torque of 180 Nm. What is the power required by the engine? (Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine Is 100% efficient.
Answer:
The applied torque from the engine is to counter prictional torques Power P = τ ω = (180) (200) = 364 kw
Question 14.
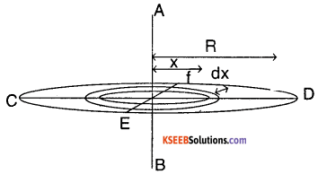
From a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting fiat body.
Answer:
Let the initial mass entire disk = M
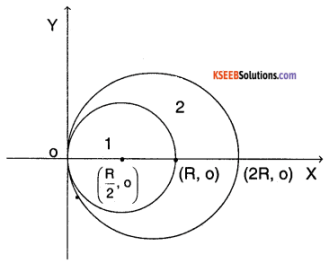
∴ Average mass/unit area = \(\frac{\mathrm{M}}{\left(\pi \mathrm{R}^{2}\right)}\)
mass of the unit cut out = \(\frac{M}{\left(\pi R^{2}\right)} \pi(R / 2)^{2}\)
= \(\frac{M}{4}\)
∴ Mass of remaining planar object = \(M-\frac{M}{4}=\frac{3 M}{4}\)
Consider region 1. it has a mass \(\frac{\mathrm{M}}{4}\) and has a centre of mass at \(\left(\frac{\mathrm{R}}{2}, 0\right)\)
Let the plane 2 has a centre of mass at (Xcm, Ycm) and has a man of \(\frac{3 \mathrm{M}}{4}\)
For the entire disc of radius R, the CM lies at (R, O)
From the definition, Rcm = \(\frac{\sum m_{i} r_{i}}{\sum m_{i}}\)

∴ The new CM is at \(\left(\frac{7 R}{6}, 0\right)\)
Question 15.
A metre stick is balanced on a knife-edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
Answer:
Figure shows all the forces on the stick
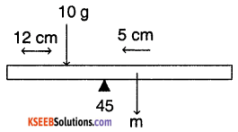
The mass of metre stick is concentrated at CM = 50cm
Consider the torques around 0 .Since the stick is in rotational equilibrium,
\(\bar{\tau}_{\mathrm{ext}}\) = m (5cm) – (10g) (45 – 12) = 0
∴ m = 10g \(\frac{(33 \mathrm{cm})}{(5 \mathrm{cm})}\) = 66 gm.
Question 16.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination,
- Will it reach the bottom with the same speed in each case?
- Will it take longer to roll down one plane than the other?
- If so, which one and why?
Answer:
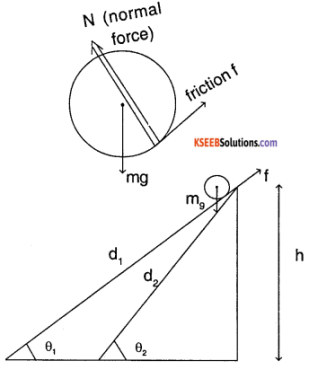
Let us assume that the sphere does not slip while rotating, then
d (distance covered) = r θ (angle covered)
v (linear velocity) = r ω (angular velocity)
a (linear acceleration) = r α (angular acceleration)
Let m be mass of sphere and r be the radius. Consider forces along the plane
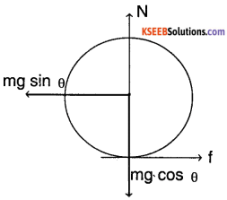
N = mg cosθ
mg sinθ – f = m α ……… (1)
f.r = 1 α
f.r = \(\frac{2}{5}\)mr² \(\left(\frac{\mathrm{a}}{r}\right)\)
⇒ f = \(\frac{2}{5}\) ma
∴ mg sin θ = \(\frac{7}{5}\) ma
∴ a = \(\frac{5}{7}\) g sin θ
By the law of conservation of energy,

∴ speed at which the sphere reaches the bottom is independent of inclination.
Also, distance on plane d = \(\frac{\mathrm{h}}{\sin \theta}\) and d = \(\frac{1}{2}\) a t²
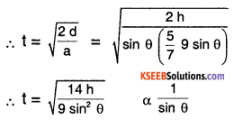
Hence higher the inclination faster will the sphere come down, i.e., t (θ1) > t (θ2)
Question 17.
A loop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
Answer:
The amount of work that has to be done is equal to the kinetic energy of loop
∴ W (work) = \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) 1 ω²
= \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) (m r²) \(\frac{v^{2}}{r^{2}}\) = mv²
= (100) (0.2)² = 4J
Question 18.
The oxygen molecule has a mass of 5.30 × 10-26 kg and a moment of Inertia of 1.94 × 10-46 kg m² about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation Is two-thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
Answer:
Given , m = 5.30 × 10-26kg,
I = 1.94 × 10-26 kgm² and
V = 500 m/s
KE (translation) = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\) × (5.30 × 10-26) (500)²
= 6.625 × 10-21J
given that,
KE (rotation) = \(\left(\frac{2}{3}\right)\) KE (translation)

= 6.748 × 1012 rad/sec
Question 19.
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
- How far will the cylinder go up the plane?
- How long will it take to return to the bottom?
Answer:
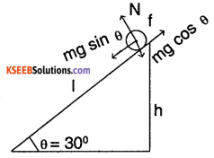
From the figure
h = I sin θ ………. (1)
1. Using principle of conservation of energy,
mgh = \(\frac{1}{2}\) mv² + I ω²
= \(\frac{1}{2}\) mv² + \(\frac{1}{2}\left(\frac{m r^{2}}{2}\right)\left(\frac{V^{2}}{r^{2}}\right)\)
[Assuming no slipping of cylinder]
mgh = \(\frac{3}{4}\) mv²
⇒ h = \(\frac{3 \mathrm{V}^{2}}{4 \mathrm{g}}\) = \(\frac{3 \times(5)^{2}}{4 \times 9.8}\) = 1.91 m
I = \(\frac{\mathrm{h}}{\sin \left(30^{\circ}\right)}\) = 3.83 m
2. Time taken to reach the bottom = 2T. The acceleration of cylinder along plane = a
∴ I = uT + \(\frac{\mathrm{h}}{\sin \left(30^{\circ}\right)}\) (a) T² …………. (2)
∴ T = \(\sqrt{\frac{2I}{a}}\)
also mg sin θ – f = ma ……………. (3)
f.r = 1 α = \(\frac{m r^{2}}{2} \times \frac{a}{r}\)
∴ f = \(\frac{\mathrm{ma}}{2}\)
⇒ mg sin θ = \(\frac{3 \mathrm{ma}}{2}\)
∴ a = \(\frac{2}{3}\) g sin θ
∴ Time taken to reach botton = 2T
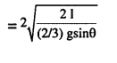
= \(\sqrt[2]{\frac{(3.83)}{(9.8)^{1 / 2}}}\)
= 3.06 sec.
![]()
Question 20.
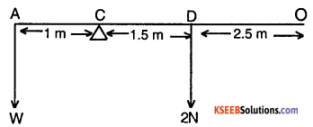
As shown in Fig.7.40, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m/s²)
(Hint: Consider the equilibrium of each side of the ladder separately.)
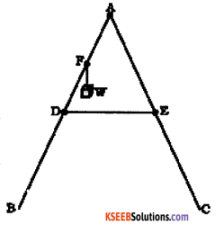
Answer:
Consider the free body diagram (FBD)
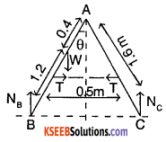
Consider all the forces on the entire ladder system. Since the ladder is in translational equilibrium;
NB + NC – W = 0 and
W = mg = 40 × 9.8 = 392N
NB + NC = 392 ………….. (1)
Also, each leg of the ladder is in rotational equilibrium. Hence torque (external) about A for each leg is zero.
To find θ,
sin θ = \(\frac{0.25}{0.8}=\frac{5}{16}\) ≈ 18.21°
⇒ cos θ = 0.9499
∴ (1.6 sin θ) NB – W (0.4 sin Q) – T (0.8 cos θ) = 0
⇒ NB = \(\frac{(392 \times 0.4 \sin \theta)+\mathrm{T}(0.8 \cos \theta)}{(1.6 \sin \theta)}\)
similarly (for right leg)
Nc (1.6 sin θ) = T (0.8 cos θ) …………………. (3)
from (2), (3) and (1)
(392) (1.6 sin θ) = T (1.6 cos θ) + (392) (0.4 sin θ)
∴ T = \(\frac{(392)(\sin \theta)}{(1.6 \cos \theta)}(1.2)\)
= 96.72 N
(from (3)) NC = \(\frac{T \cos \theta}{2 \sin \theta}\) = 146.997 N ≈ 147 N
from (1) NB = 392 – NC = 245 N.
Question 21.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. it is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint: The moment of inertia of the door about the vertical axis at one end is ML²I³.)
Answer:
Consider the door in the figure
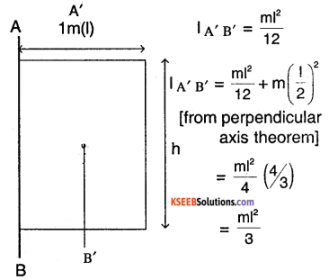
Mass of the bullet, mB = 100gm
velocity of bullet, V = 500 m/s
Mass of door, M = 12kg
width of door, I = 1 m
since there is no frictional torque on the doors, the angular momentum is conserved for door bullet system.
∴ L (initial) = L( final)
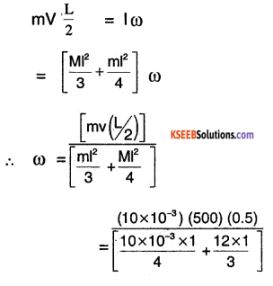
≈ 0.625 rad/sec
Question 22.
Two discs of moments of Inertia I1 and I2 about their respective axes (normal to the disc and. passing through the centre), and rotating with angular speeds ω1, and ω2 are brought Into contact face to face with their axes of rotation coincident.
- What is the angular speed of the two-disc system?
- show that the kinetic energy of the combined system is less than the sum of the Initial kinetic, energies of the two discs. How do you account for this loss In energy? Take ω1 ≠ ω2.
Answer:
1. Since there is no external torque acting on 2-disc system, the angular momentum is conserved
I1 ω1 + I2 ω2 = (I1 + I2)ω
ω = \(\frac{1, \omega_{1}+l_{2} \omega_{2}}{\left(l_{1}-l_{2}\right)}\)
2. (kinetic energy) KEinitial

some amount of kinetic energy is last due to frictional contact which brings the 2 discs to a common angular speed
\(\omega=\frac{l_{1} \omega_{1}+l_{2} \omega_{2}}{\left(l_{1}+l_{2}\right)}\)
Question 23.
- Prove the theorem of perpendicular axes. (Hint: Square of the distance of a point (x, y) in the x-y plane from an axis through the origin perpendicular to the plane is x2 + y2).
- Prove the theorem of parallel axes. (Hint: If the centre of mass is chosen to be the origin = Σ miri = 0).
Answer:
1. Consider the figure. Let M be a point mass ‘m’ in the XY plane of a plane lamina let the point lie at (x,y)
The M.L of particle M about perpendicular axis
AB = mr² = m (x² + y²) [∵r² = x² + y²]
∴ M.I. of the entire plane lamina is
IAB = Σ miri²
Izz = IAB = Σ mi (xi² + yi²)
∴ Iz = Σ mi xi² + Σ mi yi
∴ Iz = Iz + Iy.
Hence the perpendicular axis theorem is proved.
2. Consider the figure, let M be a point on the solid object, with a mass m.
let an axis CD pan through the center of mass of the solid object. Let AB be a parallel axis to the CD. Then
ICD = Σ miri² ………… (1)
and IAB = Σ mi (d + ri)²
= Σ mi d² + Σ miri² + 2 Σ miri
= Md² + 1m + 0
[Σ miri = 0, due to symmetry since the CM exists on the axis CD]
∴ IAB = ICD + M d²
(M is the total mass of solid object)
∴ The parallel axis theorem is proved.
![]()
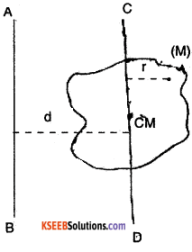
Question 24.
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) af the bottom of an inclined plane of a height h is given by v² = \(\frac{2 \mathrm{gh}}{\left(1+\mathrm{k}^{2} / \mathrm{R}^{2}\right)}\), using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Answer:
Consider the figure
Let R be the radius of the body and k be the radius of gyration about its axis of symmetry let the body have a man m and initial height is h
∴ I = mk² …………. (1)
The body translates without slipping.
∴ v = r ω ……………(2)
Also, at any point of time, the friction does not do any work, since the point of contact to plane has zero velocity.
∴ The only work done is by gravity
∴ mgh = \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) Iω²
= \(\frac{1}{2}\) mv² + \(\frac{1}{2}\left(m k^{2}\right)\left(\frac{v^{2}}{r^{2}}\right)\)
∴ v² = \(\frac{2 g h}{\left(1+k^{2} / r^{2}\right)^{(6)}}\)
Question 25.
A disc rotating about its axis with angular speed ωo is placed on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in Fig. ? Will the disc roll in the direction indicated?
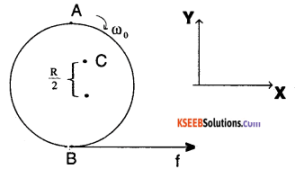
Answer:
The entire disc is rotating with an angular velocity of ωo. Hence point c has instantaneous speed of R/2ωo towards x deviation similarly A has a speed of R ωo towards X and B has a speed of ωoR towards negative X.
Question 26.
Explain why friction is necessary to make the disc in Fig. 7.41 roll in the direction indicated.
- Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
- What is the force of friction after perfect rolling begins?
Answer:
1. Frictional force opposes the movement of point B in the negative X direction, hence it is in the direction of x i.e., positive X. The sense of torque provided by friction is such that it opposes angular velocity ωo.
2. Once the perfect rolling begins, there is no external force on disc, since it does not undergo angular or linear acceleration.
Hence friction force is zero.
Question 27.
A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with initial angular speed equal to 10π rad s-1. Which of the two will start to roll earlier? The coefficient of kinetic friction is μk = 0.2.
Answer:
Consider the figure
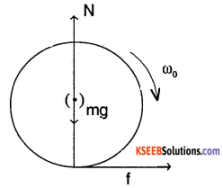
F = ma = f = μk mg
also μk mg R = -I α (torque)
∴ μk mg R = \(-\alpha \frac{m R^{2}}{2}-\frac{m R^{2}}{2}\) (for a disc)
∴ α = \(\frac{2 \mu_{\mathrm{k}} \mathrm{g}}{\mathrm{R}}\)
∴ ω = ωo + α = ωo – \(\frac{2 \mu_{k} g t}{R}\)
similarly μk mg = ma
∴ V = u + at = μk gt
when rolling begins, friction stops. Hence
v = r ω , at that time
∴ μkg T = R ωo – 2 μkg T
⇒ T1 = \(\frac{\mathrm{R} \omega_{0}}{3 \mu_{\mathrm{k}} \mathrm{g}}\) = \(\frac{10 \times 10^{-2} \times 10 \pi}{3 \times 0.2 \times 10}\) ≈ 0.52 sec (for a disc)
similarly (for ring)
T2 = \(\frac{\mathrm{R} \omega_{0}}{2 \mu_{\mathrm{k}} \mathrm{g}}\) ≈ 0.78 sec
Hence disc begin to roll earlier.
Question 28.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction is μs = 0.25.
- How much is the force of friction acting on the cylinder?
- What is the work done against friction during rolling?
- If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
Answer:
1. Consider the figure
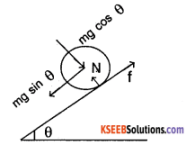
N= mg cos θ …………….. (1)
f ≤ μs N (if not slipping)
= μs mg cos θ
also mg sin θ – f = ma ………(2)
f.R = 1 α = \(\frac{m R^{2}}{2}\) α M.1. of cylinder
⇒ f = \(\frac{\mathrm{ma}}{2}\)
∴ a = \(\frac{2 g \sin \theta}{3}\)
∴ f = \(\frac{m g \sin \theta}{3}=\frac{10 \times 10 \times \sin 30}{3}\) ≈ 16.6 N
2. Since, the cylinder, is rolling, the point of its contact with plane is stationery hence the power delivered by friction is zero, hence the work done is zero.
3. Slipping occurs when
f ≥ μs mg cos θ
⇒ \(\frac{\mathrm{mg} \sin \theta}{3}\) ≥ μs mg cos θ
⇒ tan θ ≥ μs × 3 = 0.75
⇒ θ ≥ 37°
1st PUC Physics System of Particles and Rotational Motion One Mark Questions and Answers
Question 1.
State the law of moments.
Answer:
The algebraic sum of the moments of any number of forces about Any point is equal to the moment of their resultant about the same point.
Question 2.
What is moment of a couple?
Answer:
The rotating ability of the couple is called moment of the couple. It is measured by the product of the force and the arm of the couple.
Question 3.
What is the dimensional formula of moment of force?
Answer:
ML² T-2
Question 4.
Give the expression for resultant of 2 like parallel forces.
Answer:
Resultant force of two like parallel forces R = P + Q. Where P and Q are the magnitudes of like parallel forces.
Question 5.
When is the moment of force positive?
Answer:
When force rotates the body in an anti-clockwise direction, moment of a force is positive.
Question 6.
What is a rigid body?
Answer:
A rigid body is the one in which the distance between any two particles remains the same even under the action of external forces.
![]()
Question 7.
Define the term angular acceleration.
Answer:
Rate of change of angular velocity of a body is called the angular acceleration.
Question 8.
What is the unit of moment of inertia?
Answer:
kgm²
Question 9.
What is the dimensional formula of moment of inertia?
Answer:
ML²
Question 10.
Define the radius of gyration.
Answer:
Radius of gyration of a body about an axis is defined as the distance from the axis at which the entire mass of the body must be concentrated in order to give the same moment of inertia of the body about the given axis.
Question 11.
Define the following.
A dancer standing on a rotating table raises her hands suddenly what happens?
Answer:
The moment of inertia increases & angular velocity decreases.
Question 12.
What is a couple?
Answer:
Two equal unlike parallel forces acting at two different points of a rigid body constitute a couple.
1st PUC Physics System of Particles and Rotational Motion Two Marks Questions and Answers
Question 1
Define a couple. Give examples.
Answer:
Two equal unlike parallel forces acting at two different points on a rigid body constitute a couple.
E.g.
- Pedalling a bicycle.
- Spinning a top
- Opening or closing a tap
- Turning the steering wheel of a vehicle.
Question 2.
State the condition of equilibrium of a system of coplanar parallel forces.
Answer:
The condition of equilibrium of a body acted upon by a number of parallel forces is,
1. Algebraic sum of the forces must be zero. i.e., Sum of the forces acting in the upward direction must be equal to the sum of the forces acting in the downward direction.
2. The algebraic sum of the moments of the forces about any point in their plane must be zero. i.e., Sum of the moments of the forces about a point in the anticlockwise direction is equal to the sum of the moments of the forces about the same point in the clockwise direction.
![]()
Question 3.
When is a body said to have rotational motion? Give an example.
Answer:
A body is said to have rotational motion if a line of points in the body remains fixed during the motion of the body.
E.g.:
- A spinning top
- A rotating wheel
Question 4.
Define angular displacement. What is its unit?
Answer:
Angular displacement of a rotating body is the angle described by a line in the body which is perpendicular to the axis of rotation. Angular displacement is measured in radians.
Question 5.
Define angular velocity. What is its unit?
Answer:
Angular velocity of a rigid body is the rate of change of angular displacement. Its unit is rads-1.
Question 6.
State the equations of rotational motion.
Answer:
The equations of motions of a body rotating with uniform acceleration is,
ω2 = ω1 + at
θ = ω1t + \(\frac{1}{2}\)αt²
ω2² =ω1² + 2 α θ
where
ω1 = initial angular velocity,
ω2 = final angular velocity,
t – time taken,
α – angular aceleration and
θ – angular displacement.
Question 7.
Derive the relation between linear and angular velocity, or Derive v = rw
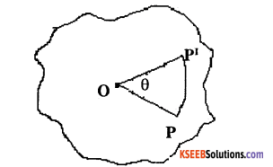
Answer:
Consider a body rotating about an axis passing through a point O and perpendicular to the plane of the paper. Let P be the position of a particle inside the body. If the body rotates through an angle 0 in a time interval of t, the particle at P reaches P’.
∴ Linear displacement \(\mathrm{PP}^{\prime}\) = r θ
∴ Linear velocity, v = \(\frac{\mathrm{PP}^{\prime}}{t}=\frac{r \theta}{t}\)
But \(\frac{\theta}{\mathfrak{t}}\) = ω, the angular velocity
∴ Linear velocity, v = r ω
Question 8.
Two spheres, one made of wood and the other made of iron have the same mass. Which of the two spheres has got greater moment of inertia about the diameter? Why?
Answer:
Moment of inertia of a solid sphere about the diameter I= \(\frac{2}{5}\) MR². Since M & R is the same. I depend on R. Since R is less for ironwood has a greater moment of inertia.
Question 9.
Define Torque and angular momentum. Mention their units. Give the relation between them
Answer:
The turning effect of a force is called Torque. The angular momentum of the body is defined as the moment of momentum about the axis of rotation. The relation between Torque & angular momentum is L = \(\frac{\tau \omega}{\alpha}\).
Question 10.
Give unit & dimension of torque.
Answer:
Unit is Nm.
Dimension is M1L2T-2.
![]()
Question 11.
What is the relation between linear & angular momentum? Explain the terms.
Answer:
Relation between linear & angular momentum is \(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}\) where ‘L’ is the angular momentum
p – linear momentum
r – perpendicular distance from the axis of rotation.
1st PUC Physics System of Particles and Rotational Motion FourFive Marks Questions and Answers
Question 1.
Find the resultant of two like parallel forces using the law of moments.
Answer:
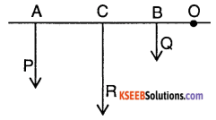
Let P and Q be two like parallel forces acting at the points A and B on a rigid body. Let R be the resultant of P and Q acting at C. According to the law of moments, moment of forces about C is P × AC – Q × CB = 0
P × AC = Q × CB ………………. (1)
According to the law of moments, moment of forces about O
P × OA + Q × OB = R × OC
P (OC + AC) + Q × (OC – CB) = R × OC
P × OC + P × AC + Q × OC – Q × CB = R × OC
P × OC + Q × CB + Q × OC – Q × CB = R × OC From (1)
P × OC + Q × OC = R × OC
P + Q = R
Hence the resultant of two like parallel forces acting on a body is sum of the individual forces and point of application of it divides the line joining the points of application of individual forces internally in the inverse ratio of the forces.
Question 2.
What is torque? Derive an expression for the torque acting on a rotating body.
Answer:
The turning effect of a force is called moment of force or torque. It is measured by the product of the force and the perpendicular distance of the line of action of force and axis of rotation. Thus, torque = force × perpendicular distance from the axis of rotation.
Torque τ = F × r = mar = mr²α
∵ α = r α
For the entire body τ = (Σ mr²) α = I α.
∵ Σ mr² = I, the moment of inertia and α is angular acceleration.
Question 3.
What is angular momentum? Derive an expression for the angular momentum of a rotating body.
Answer:
The angular momentum of the particle is defined as the moment of momentum about the axis of rotation.
∴ Angular momentum = linear momentum x perpendicular distance from the axis.
If ω is the angular velocity of the particle, then the linear velocity v = r ω.
∴ Angular momentum of each particle = (mv)r = (mrω) r = mr²ω.
∴ Total angular momnetum of the body is L = (Σ mr²ω) = (Σ mr²) ω = lω where l = Σ mr².
Question 4.
Define moment of Inertia. On what factors does it depend? Derive the expression for the moment of inertia of a rigid body.
Answer:
The rotational inertia of a body is called its moment of inertia denoted by I. The Moment of inertia depends on:
1. The size and shape of the body.
2. The axis of rotation.
3. The distribution of mass about the axis. The moment of inertia of a body about a given axis is the sum of the products of the masses of each particles and squares of their perpendicular distances from the axis of rotation.
Let m1, m2, m3 ………….. are the masses of the particles of the body situated at distance r1, r2, r3 …………… from the axis of rotation then,
I = m1r1² + m2r2² + m3r3² + …………..
I = Σ mr².
Question 5.
Write expression for moment of inertia of
- thin rod
- ring
- cylinder
- sphere.
Answer:
1. Moment of inertia of a thin rod of length L and mass M about an axis passing through its centre and perpendicular to its length is,
I = \(\frac{M L^{2}}{12}\)
2.
- Moment of inertia of a circular ring of radius R and mass M about an axis passing through the diameter is,
I = \(\frac{M R^{2}}{2}\) - Moment of inertia of a circular ring of radius R and mass M about an axis passing through the centre and perpendicular to its plane is,
I = MR²
3. Moment of inertia of a cylinder of radius R and length L and mass M about an axis passing through the axis is
I = \(\frac{M R^{2}}{2}\)
4. Moment of inertia of a solid sphere of radius R and mass M passing through the diameter is
I = \(\frac{2}{5}\)MR²
Question 6.
State and explain the law of conservation of angular momentum. Give two examples to illustrate the law.
Answer:
Law of conservation of angular momentum states that in the absence of an external torque, the total angular momentum is conserved or the total angular momentum of an isolated system remains constant both in magnitude and direction.
If ω1 is the angular velocity when the moment of inertia is I1 and ω2 is the angular velocity when the moment of inertia is I2, then from the law of conservation of angular momentum it follows that I1, ω1 = I2 ω2
Examples:
1. A spinning ballet dancer uses the principle of conservation of angular velocity to increase her angular velocity. She first spins her arms and one of her legs. The moment of inertia about the axis of rotation is large. Consequently, her angular speed is small. She then folds her arms and brings the stretched leg closer to the other leg. As a result of her moment of inertia about, the axis of rotation decreases and her angular speed increases.
2. A diver jumping from a springboard folds his arms and legs inwards and curls his body. As a result, his moment of inertia decreases. He then somersaults in the air with a large angular speed. Just before touching the surface water he stretches his limbs. His moment of inertia increases. Consequently, his angular speed decreases. He thus strikes water with lower speed.
![]()
Question 7.
State the theorem of parallel and perpendicular axis.
Answer:
According to the parallel axis theorem, a moment of inertia of a body about any axis is equal to the sum of the moment of inertia about a parallel axis through the centre of gravity and the product of the mass of the body and the square of the perpendicular distance between the two axis.
Let Ic be the moment of inertia of a body of mass M about an axis (PQ) passing through the centre of gravity C. According to the theorem moment of inertia of a body an axis AB is I = lc + Mr² According to the theorem on perpendicular axis, the moment of inertia of a plane about an axis perpendicular to the plane is equal to the sum of the moment of inertia about two perpendicular axes in the plane of the lamina such that the three mutually perpendicular axes have common point of intersection.
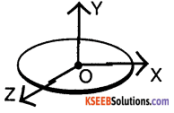
If IX, IY and IZ represent the moment of inertia of the body about the axes OX, OY & OZ, then according to perpendicular axes theorem IX + IZ = IY.
Question 8.
Compare translatory and rotatory motion.
Answer:
| Translational motion | Rotational motion |
| Body has linear velocity. | Body has angular velocity. |
| Body has linear momentum p = mv. | Body has angular momentum L = I ω. |
| Acceleration a= dv/dt. | Angular acceleration a = d w /dt. |
| Kinetic energy = (1/2 )mv2 | Rotational K.E = (1/2)Iω2 |
| Work done W = FS | Work done = τ ω |
Question 9.
Define the following
- Angular velocity
- Angular acceleration
- Angular momentum
- Torque
- Centripetal acceleration
Answer:
- Angular velocity is defined as the rate of angular displacement of the rotating body.
- Angular acceleration is defined as rate of change of angular velocity of the rotating body.
- Angular momentum is defined as the moment of linear momentum of the rotating body.
- Toque is defined as the moment of the force about the axis of rotation acting on the rigid body.
- In uniform circular motion the acceleration produced on the body which acts along the radius, towards the center of the circular path is defined as the centripetal acceleration.
1st PUC Physics System of Particles and Rotational Motion Numerical Problems Questions and Answers
Question 1.
A uniform bar 4 metres long and weighing 2 N is resting on a knife edge at 0.8m from one end. What weight suspended from the end to keep the bar horizontal?
Answer:
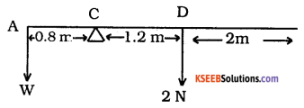
The weight 2N of the bar acts at its midpoint D. Let C be the position of the knife edge and W be the weight suspended at the end A which keeps the bar horizontal.
Taking moments about C
W × AC = 2 × CD
W × 0.8 = 2 × 1.2
W = \(\frac{2 \times 1.2}{0.8}\)
= 3 N.
To keep the bar horizontal the weight to be suspended is 3 N.
Question 2.
A boy and a man carry a load of 100kg attached to the light pole of length 4 metres where must be the load be attached if the boy must bare only 1/4 of the weight.
Answer:
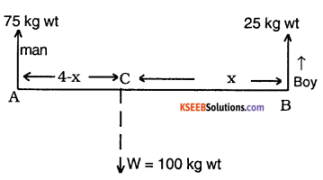
Let the load be attached at a distance x from the ‘boy’s end.
Taking moments about C,
75 × AC = 25 × BC
75 × (4 – x) = 25 × x.
300 – 75x = 25 x
300 = 100x or x = 3m.
Therefore the load must be attached at a distance of 3 metres from the boys end.
![]()
Question 3.
A uniform rod of length 1m and mass 20 kg Is supported horizontally on 2 knife edges at the ends. Two masses of 6 kg and 10 kg are suspended at 0.3m and 0.7m from one end of the rod. Find the reactions on the knife edges.
Answer:
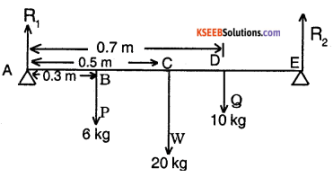
Sum of the upward forces = sum of the downward forces.
R1 + R2 = P + Q + W = 6 + 10 + 20
= 36 kg wt.
Taking moments about A
P × AB + W × AC + Q × AD = R2 × AE
6 × 0.3 + 20 × 0.5 + 10 × 0.7 = R2 × 1
1.8 + 10 + 7 = R2 = 18.8kgwt
R1 + 18.8 = 36
R1 = 17.2 kg wt
Question 4.
Five bodies 1 kg wt., 2kg wt., 3kg wt., 4kg wt. and 5kg wt. are suspended at a distances of 1m, 2m, 3m, 4m, and 5 m from one end of a uniform rod of mass 4kg and 6 metres length. Find the point about which the rod will balance about the knife edge placed at a distance of ‘x’ from the end A.
Answer:
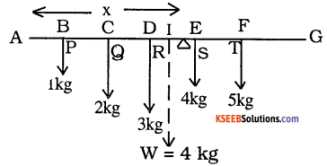
Resultant force acting vertically downwards on the rod
=P + Q + R + S + T + W
= 1 + 2 + 3 + 4 + 5 + 4 = 19 kg wt
Thus force of 19 kgwt. acting vertically upwards will balance the rod. This force acts at a distance ‘x’ from A.
i.e., R1 = 19 kgwt.
Taking the moments about A,
P × AB + Q × AC + R × AD + S × AE + T × AF + W × Al = R1x.
1 × 1 + 2 × 2 + 3 × 3 + 4 × 4 + 5 × 5 + 4 × 3 = R1x = 19x.
1 + 4 + 9 + 16 + 25 + 12 = 19x.
67 = 19x or x = \(\frac{67}{19}\) = 3.52m
∴ Distance of the knife edge from the end A is 3.52m.
Question 5.
A ladder of mass 10kg and length of 4 metres rests with one end against a smooth vertical wall and the other end against a smooth floor. The ladder is inclined at 60° to the horizontal. Calculate the horizontal force to be applied to the lower end to prevent from sliding down.
Answer:
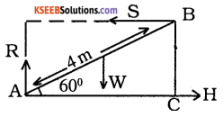
The forces acting on the ladder to keep it in equilibrium are,
- Its own weight W vertically downwards at its midpoint.
- Normal reaction R of the floor at the end A and S of the wall at the end B.
- The horizontal force H at the end A towards the wall.
Since the ladder is in equilibrium, Horizontal force must be equal to S Vertical force must be equal to W. Taking moments about A,
S × 4 × sin 60 = 2 × W × cos 60
But, W = 10 kg wt
∴ S × 4 x sin 60 = 2 × 10 × cos60
S = 5 \(\frac{\cos 60}{\sin 60}\) = \(\frac{5}{\tan 60}\) = \(\frac{5}{\sqrt{3}}\)
Horizontal force required = \(\frac{5}{\sqrt{3}}\) kg wt.
= 2.887 kg wt.
Question 6.
A uniform rod of length 0.5m and weighting 0.3kg is supported horizontally on two knife edges at the ends. Two masses of 5kg and 8kg are suspended at 0.2m and 0.35m from one end of the rod. Find the reaction on the knife edges.
Answer:
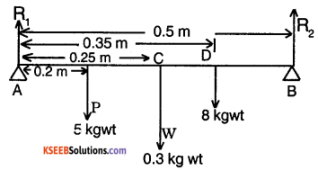
Since the rod is in equilibrium, sum of upward forces = sum of downward forces
R1 + R2 = 5 + 0.3 + 8 = 13.3
Taking moments of forces about A,
R1 × O – 5 × 0.2 – 0.3 × 0.25 – 8 × 0.35 + R2 × 0.5 = 0
0.5R2 = 1 + 0.075 + 2.8
R2 = \(\frac{3.875}{0.5}\) = 7.75 kgwt
R1 = 13.3 – 7.75 = 5.55 kgwt.
Question 7.
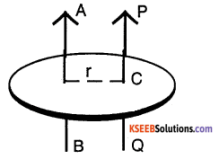
Two Boy’s weighting 30 Kg and 50 Kg are sitting on either side of the fulcrum of a see-saw at a distance of 2m and 3m respectively. Where should a man of 60 Kg must sit to balance the seesaw?
Answer:
Let the man of 60kg sit at a distnce x from c, then Taking the moments about c
P × AC + R × DC = Q × BC
30 × 2 + 60 × x = 50 × 3
60 x = 150 – 60
x = \(\frac{90}{60}\) = 1.5m.
Question 8.
A uniform bar 5m long & weighing 2N is resting on a knife edge at 1m from one end. What weight should be suspended from the end to keep the bar horizontal?
Answer:
The weight 2N of the bar acts at its midpoint D. Let C be the position of the knife edge & W be the weight suspended at the end A which keeps the bar horizontal. Taking moments about C
W × AC = 2 × OD
W × 1 = 2 × 2.5
W = \(\frac{2 \times 2.5}{1}\) = 5N
To keep the bar horizontal the weight to be suspended is 5N.
Question 9.
A body rotates along a circle of radius 0.2 m with a speed of 240 rotations per minute. Calculate
- angular speed
- linear speed
- If the speed of rotation changes to 330 rotations per minute in 10 seconds, calculate the angular and linear acceleration.
Answer:
The angular velocity is given by
ω1 = \(\frac{2 \pi n_{1}}{t}\) rads-1
Here n1 = 240,
t = 1 min = 60 s.
∴ Initial angular velocity
= \(\frac{2 \pi \times 240}{60}\) = 8π rads-1
Initial linear velocity
v1 = rω1;
Here, r = 0.2 m
∴ v1 = 0.20 × 8π
= 5.02 ms-1
∴ Final angular velocity
= ω2 = \(\frac{2 \pi \times n_{2}}{t}\)
= \(\frac{2 \pi \times 330}{60}\) = 11π rads-1
∴ Final linear velocity v2 = rω2
= 0.2 × 11π = 6.91 ms-1
From the equation of motion, we have,
ω2 = ω1 + at
∴ a = \(\frac{\omega_{2}-\omega_{1}}{t}\)
Here, ω2 = 11π,
ω1 = 8 π,
t = 10 s
∴ α = \(\frac{\omega_{2}-\omega_{1}}{t}\)
= \(\frac{11 \pi-8 \pi}{10}\)
= \(\frac{3 \pi}{10}\) = 0.3π rads-2
Linear acceleration is
a = rα = 0.2 × 0.3π
= 0.188 ms-2
![]()
Question 10.
A uniform rod of mass 8kg and length 4m rotates at the rate of 60 rotation per minute about an axis passing through the centre and perpendicular to its plane. If the speed of rotation changes to 80 rpm in 10 seconds.Calculate the torque applied
Answer:
Moment of inertia of the rod of length L and mass M about an axis passing through the centre and perpendicular to its plane is given by,
I =\(\frac{M L^{2}}{12}=\frac{8 \times 4 \times 4}{12}\)
= 10.67 kg.m2
Initial angular velocity,
ω1 = \(\frac{2 \pi n_{1}}{t}\)
= \(\frac{2 \pi \times 60}{60}\) = 2 πrads-1
Final angular velocity,
ω2 = \(\frac{2 \pi n_{2}}{t}\)
= \(\frac{2 \pi \times 80}{60}\) = 2.67 πrads-1
Angular acceleration is given by ,
α = \(\frac{\omega_{2}-\omega_{1}}{t}\)
= \(\frac{2.67 \pi-2 \pi}{10}\)
= 0.067 πrads-2
∴ Torque applied τ = I α
= 10.67 × 0.067 × π
= 2.24 Nm.
Question 11.
A flywheel of mass 100 kg and radius of 0.8m makes 120 revolutions per minute calculate
- angular velocity
- moment of inertia about the axis of rotation.
Solution:
1. Angular velocity
ω = \(\frac{2 \pi n}{t}\)
Here n = 120,
t = 60s
∴ ω = \(\frac{2 \pi \times 120}{60}\) = 4π rads-1
2. Fly wheel is in the form of a circular disc. Therefore moment of inertia about an axis passing through its centre and perpendicular to its plane is given by,
I = \(\frac{\mathrm{MR}^{2}}{2}\)
= \(\frac{100 \times 0.8 \times 0.8}{2}\) = 32 kg m²
Question 12.
The angular velocity of a flywheel decreases uniformly from 1200 revolution per minute to 600 rpm in 5 seconds. Find the angular acceleration.
Answer:
a. Initial angular velocity ω1 = 2πn1
Here n1 = \(\frac{1200}{60}\) = 20 rps
ω1 = 2πn1
= 2 × π × 20 = 40π rads-1
Final angular velocity ω2 = 2πn2
Here n2 = \(\frac{600}{60}\) = 10 rps
∴ ω2 = 2 × π × n2
= 2 × π × 10 = 20π rads-1
Angular acceleration
a = \(\frac{\omega_{2}-\omega_{1}}{t}=\frac{20 \pi-40 \pi}{5}=\frac{-20 \pi}{5}\) = -4π
i.e. a = 12.57 rad s-2. Therefore angular retardation is 12.57 rad s-2.
Question 13.
An automobile engine is idling at 500 rpm. When the accelerator is depressed, the angular velocity increases to 3000 rpm, in 5 seconds. Assuming the acceleration to be constant, find
- The initial and final angular revolutions expressed in rads-1
- Angular acceleration
- The number of revolution made by the engine during this interval
- Final linear velocity if the radius of the flywheel attached to the engine is 15cm.
Answer:
1. Initial angular velocity ω1 = 2πn1
Here n1 = \(\frac{500}{60}\) = 8.333 rps
∴ ω1 = 2πn1
= 2 × 3.142 × 8.333
= 52.33 rads-1
Final angular velocity ω2 = 2πn2
Here n2 = \(\frac{3000}{60}\) = 50
∴ ω2 = 2 × π × n2
= 2 × 3.142 × 50 = 314.2 rads-1
2. angular acceleration,
α = \(\frac{\omega_{2}-\omega_{1}}{t}=\frac{314.2-52.33}{5}\)
= 52.31 rads-2
3. angular displacement
θ = ω1 t + \(\frac{1}{2}\) αt²
= 52.33 × 5 + \(\frac{1}{2}\) × 52.31 × 25
= 915.5 revolutions
∴ number of revolutions
r = \(\frac{\theta}{2 \pi}=\frac{915.5}{2 \times 3.142}\) = 145.2 rad
4. Final linear velocity
v2= rω2 = 0.15 × 314.2 = 47.12 ms-1
![]()
Question 14.
What is a rigid body? State and explain parallel and perpendicular axes theorem of moment of inertia.
Answer:
Rigid body:
Rigid body is the one which is not deformed under the action of external force.
According to the parallel axis theorem, a moment of inertia of a body about any axis is equal to the sum of the moment of inertia about a parallel axis through the centre of gravity and the product of the mass of the body and the square of the perpendicular distance between the two axis.
Let Ic be the moment of inertia of a body of mass M about an axis (PQ) passing through the centre of gravity C. According to the theorem moment of inertia of a body, an axis AB is I = lc + Mr² According to the theorem on perpendicular axis, the moment of inertia of a plane about an axis perpendicular to the plane is equal to the sum of the moment of inertia about two perpendicular axes in the plane of the lamina such that the three mutually perpendicular axes have common point of intersection.
If IX, IY and IZ represent the moment of inertia of the body about the axes OX, OY & OZ, then according to perpendicular axes theorem IX + IZ = IY.
Question 15.
A boy balances a pair of equal masses on a uniform massless rod of length 1 m at its midpoint.
- Prove that the centre of gravity lies exactly at the midpoint.
- Are there any variations if masses are changed in equal proportion?
- Calculate the balancing point if only one of the mass is doubled.
Answer:
1.
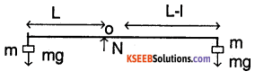
consider the free body diagram (FBD) shown in the figure. N is the normal force applied by boy. Since the system is in rotational equilibrium about 0.
∴ mgl = mg (L – l)
∴ 2 l = L ⇒ l = \(\frac{\mathrm{L}}{2}\)
Hence the centre of gravity lies exactly
at the mid pointmid point of rod.
2. No, the centre of gravity does not change.
3. Consider the FBD
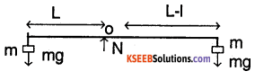
The rod is balanced about 0 (balancing point)
∴ 2mgl = mg (L – l)
∴ 3L = L
⇒ l = \(\frac{\mathrm{L}}{3}\) from 2m.
Question 16.
The figure illustrates the position and masses of 3 particles. Find the position of their centre of mass.
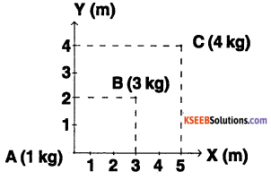
Answer:
The position A is (0, 0, 0)
The position of B is (3, 2, 0)
The position of C is (5, 4, 0)

The position of centre of mass of system is (3.625, 2.75, 0).
Question 17.
A radioactive nucleus at rest spontaneously decays into 2 fragments of mass ratio 2:3. If the first one flies along the positive X – axis.
- In which direction does the other fragment fly?
- Which law is applied in finding the answer?
- State the law.
Answer:
1. Since the radio active nucleus was initially at rest and spontaneously bursts, there is no external force on the system. Hence the linear momentum of system is conserved. Since the linear momentum was zero initially, the final momentum must also be zero. Hence the other fragment flies off in the negative direction.
2. Conservation of linear momentum.
3. If no external force is acting a system of particles, then their total linear momentum remains constant.
Question 18.
A body of mass ‘m’ is moving with a velocity ‘V” about an axis at a distance of T from the axis.
- How is its linear velocity related with angular velocity?
- Derive the relation connecting torque and angular momentum.
Answer:
1. Relation between linear velocity and angular velocity is \(\overrightarrow{\mathrm{v}}=\vec{\omega} \times \vec{r}\) where V is the linear velocity and co is the angular velocity and r is the radius of rotation.
2. We know
\(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{w}} \times \overrightarrow{\mathrm{p}}\) ………………. (1)
where, L is angular momentum, r is radius of rotation and p is linear momentum of the particle. Differentiating (1) with respect to time,

Thus torque is rate of change of angular momentum.
Question 19.
- Prove that the radial component of linear momentum has no effect on the angular momentum of a particle,
- Explain the planetary motion on the basis of conservation of angular momentum.
Answer:
1. \(\overrightarrow{\mathrm{L}}\) (angular momentum) = \(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}\)
= \(\left(\begin{array}{l}{\text { position }} \\ {\text { vector }}\end{array}\right) \times\left(\begin{array}{l}{\text { linear }} \\ {\text { momentum }}\end{array}\right)\)
let \(\overrightarrow{\mathrm{p}}=\overrightarrow{\mathrm{p}}_{\mathrm{r}}+\overrightarrow{\mathrm{p}_{1}}\)
where pr is radial component parallel to \(\vec{r}\) and pt is tangential component perpendicula to \(\vec{r}\)
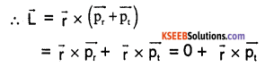
[\(\vec{r} \times \vec{p}_{r}\) = 0, since they are parallel]
∴ \(\vec{L}=\vec{r} \times \vec{p}_{t}\)
Hence the radial component of linear momentum has no effect on angular momentum.
2. Assume a body of mass ‘m’ moving with an angular momentum L. Then, areal velocity is
\(\frac{\mathrm{d} \mathrm{A}}{\mathrm{dt}}=\frac{\mathrm{L}}{2 \mathrm{m}}\)
According to kepler’s first law of planetary motion, every planet revolves round the sun in an elliptical orbit with sun at one of the foci. The centripetal force for this motion is provided by gravitational force between sun and planet and it acts along the line connecting sun and planet. Hence this force is radial (Fr) and not tangential as shown in the figure
∴ \(\vec{\tau}=\vec{r} \times \vec{F}=0\)
∴ \(\frac{d \bar{L}}{d t}\) = 0 hence L is constant.
Hence the radius vector drawn from planet to sun sweeps equal area in equal intervals of time. This is Kepler’s second law of planetary motion.
Question 20.
Consider a rigid body capable to rotate about an axis
- State the laws of motion for rotating bodies.
- If the bodies Is accelerated (rotational) uniformly, derive the equations for the angular velocity after an interval.
- Derive the equation for angular displacement after any time ‘t’.
- Derive an equation for the angle covered by a rotating rigid body (subject to uniform angular acceleration) in the nth second.
Answer:
1. Newton’s law of rotational motion.
2. Let the rigid body have a constant angular acceleration of α, then
\(\frac{\mathrm{d} \omega}{\mathrm{dt}}=\alpha\)
⇒ \(\int_{0}^{1} d \omega\) = ∫ α dt = α t
⇒ ω(t) = ω(0) + α t ……………. (1)
where ω(t) is angular velocity at time t ω(0) is the initial angular velocity of body,
3. Let θ (t) be the angular displacement in the time interval
we know
\(\frac{\mathrm{d} \theta(\mathrm{t})}{\mathrm{dt}}\) = ω(t) = ω(0) + α t (from (1))
⇒ \(\int_{0}^{t} d \theta(t)=\int_{0}^{t}[\omega(0)+\alpha t] d t\)
⇒ θ (t) – θ (0) = ω(0) + \(\frac{\alpha t^{2}}{2}\)
∴ θ (angular displacement) = ω(0) t + \(\frac{\alpha t^{2}}{2}\)
4. we know [let ω(0) = ωo]
θn = ωon + \(\frac{1}{2}\) αn²
and θn+1 = ωo (n+1) + \(\frac{1}{2}\) α(n+1)²
Angular displacement in nth second
θn = θn+1 – θn
∴ θn = {ωo (n+1) – ωo n} + \(\frac{\alpha}{2}\){(n+1)² – n²}
∴ θn = ωo + \(\frac{\alpha}{2}\) (1) (2n + 1)
= ωo + α \((n+1 / 2)\)
![]()
Question 21.
A disc of mass m and radius R is capable of rotation
- Determine its MI about an axis passing through its centre and perpendicular to its plane.
- which theorem helps in determining MI about any diameter. State it
- Find the MI about any of the diameter.
Answer:
1. Consider the diagram for finding MI of the disc
For the disc, consider a small ring of thickness ‘dx’ and radius x.
The area of the ring is
A = π (x + dx)² – πx²
= π (2x dx)
∴ mass of the ring,
m (x) = A X (massdensity)
= (2πx dx) \(\frac{M}{\left(\pi R^{2}\right)}\)
= \(\left(\frac{2 M}{R^{2}}\right)\)x dx
∴ MI of ring about the axis = mass × (radius)²
= \(\left(\frac{2 M}{R^{2}}\right)\) x dx x²
= \(\left(\frac{2 M}{R^{2}}\right)\) x³ dx
The total MI of disc about AB

∴ MIAB = \(\left(\frac{2 M}{R^{2}}\right)\)
2. Perpendicular axis theorem – The moment of inertia of plane lumina about an axis about two mutually perpendicular axis in its plane and intersecting each other at the point where the perpendicular axis meets the lamina.
3. MCD + MEF = MAB
⇒ 2MCD = MAB = \(\frac{\mathrm{MR}^{2}}{2}\)
∴ MCD = MEF = \(\frac{\mathrm{MR}^{2}}{2}\) (MI about any diameter)
Question 22.
Equal torques are applied on a sphere and a disc of the equal masses and radius. If the sphere is rotating about its diameter and the disc about its axis, which one possesses greater acceleration? and why?
Answer:
M.I. of sphere = 2/5 MR²,
M.l. of sphere = \(\frac{\mathrm{MR}^{2}}{2}\) and α = \(\frac{\tau}{1}\)
Sine M.l. the disc is greater than that of the sphere,
αdisc < αsphere
This is because
ISphere αsphere = IDisc αdisc = τ

∴ αsphere > αdisc
Question 23.
Find the moment of inertia of a disc of mass M and radius R about an axis tangential to disc and lying on the plane of the disc.
Answer:
Consider the disc in figure:
we know M.I. of disc about an axis perpendicular to disc and passing through its CM = \(\frac{\mathrm{MR}^{2}}{2}\)
Using perpendicular axis theorem
IAB + ICD = \(\|_{\perp}\) = \(\frac{\mathrm{MR}^{2}}{2}\)
⇒ 2 IAB = \(\frac{\mathrm{MR}^{2}}{2}\) [Since IAB = ICD] (symmetry)
∴ IAB = \(\frac{\mathrm{MR}^{2}}{4}\)
using parallel axis theorem
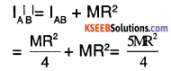
Question 24.
Distinguish between centre of gravity and centre of mass.
Answer:
1. Centre of gravity:
It is the location where the effective weight of the entire body acts.
2. Centre of mass:
It is the location where a particle having mass equal to that of the system is placed such that the Newton’s laws of motion can be applied to the entire system. If acceleration due to gravity is uniform for all the particles of the system, then centre of mass is same as the centre of gravity, otherwise not.
Question 25.
Mention the factors that influence moment of inertia of a body.
Answer:
- Distribution of mass in the body.
- Shape of the body
- Inclination of the axis of rotation.
- The axis of rotation about which to M.I. is calculated.
Question 26.
About which axis the M.I. is minimum for a rigid body?
Answer:
According to parallel axis theorem, M.I. of an axis (A’B’), parallel to an axis AB passing through centre of mass is given by IA’B’ = M.I.+ MR² where M is mass of body and R is the perpendicular distance between AB and A’B’ )
∴ IA’B’ > IAB
∴ to minimize I, R = 0
Hence M.I. of a body is minimum about an axis passing through the centre of mass.
Question 27.
Three particles are arranged as shown in the figure.
- Find the position of their centre of mass.
- Find M.I. about an axis perpendicular to plans and passing through CM.
- Find M.I. about an axis perpendicular to plane and passing through A and hence show that parallel axes theorem holds good.
- Find M.I. about AQ.
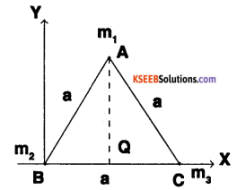
Answer:
1. Co-ordinates of B (0, 0) Co-ordinates of C (a, 0)
Co-ordinates of A \(\left(a / 2, \sqrt{3} \frac{a}{2}\right)\)
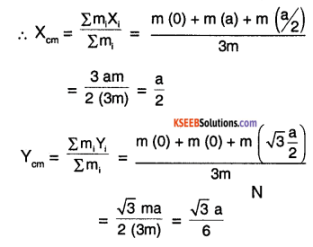
Hence CM is the centroid of the triangle as shown
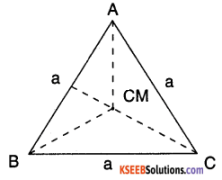
The Co-ordinates of CM is \(\left(a / 2, \frac{\sqrt{3} a}{6}\right)\)
The distance of CM from A, B, or C is same and d is
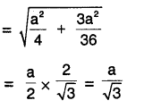
2. ICM = Σ mi xi²
= mA xA² + mB xB² + mC xC²
= 3 m \(\left(\frac{\mathrm{a}}{\sqrt{3}}\right)^{2}\) = ma²
∴ M.l. about an axis ⊥ to triangle and passing and through CM = ma²
3. M.I.about an axis perpendicular to plane and passing through A is,
IA = Σ mi xi²
= mA(0) + mB(a²) + mC(a°)
= ICM + (3m) d²

= ma² + ma² = 2ma²
LHS = RHS
Hence parallel axes theorem is verified
4. IAQ = Σ mi xi²
= mA xA² + mB xB² + mC xC²
= m (0)² + m \(\left(\frac{\mathrm{a}}{2}\right)^{2}\) + m \(\left(\frac{\mathrm{a}}{2}\right)^{2}\)
= \(\frac{\mathrm{ma}^{2}}{2}\)
![]()
Question 28.
A rod of length L and mass M held vertically Is let go down, without slipping at the point of contact. What is the velocity of the top end at the time of touching ground?
Answer:
Consider the figure to illustrate the experiment
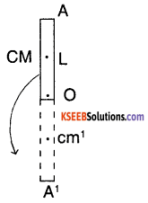
In the experiment, the CM of the rod travels from CM to CM. This change in potential energy appears as rotational kinetic energy.
To find Ml about 0,
MI (about CM) = \(\frac{\mathbf{ML}^{2}}{12}\)
using parallel axes theorem
I = I + \(\mathrm{M}\left(\frac{\mathrm{L}}{2}\right)^{2}\)
∴ I = \(\frac{M l^{2}}{12}+\frac{M l^{2}}{4}=\frac{M l^{2}}{3}\)
Now, using principle of conservation of energy
MgL = \(\frac{1}{2}\)Ioω²
∴ MgL = \(\frac{M l^{2}}{6}\) × ω²
∴ ω = \(\sqrt{\frac{6g}{L}}\)
To find the velocity of the tip A of rod
VA = rAω = L × \(\sqrt{\frac{6g}{L}}\)
= \(\sqrt{6 g L}\)
Question 29.
A uniform rod of length 1m is accelerated (2m/s²) horizontally by the application of two forces F1 and F2. The mass of the rod is 2 kg. If the force F1 acts at the top edge of the rod and F2 acts at a distance 25cm from the lower edge in the opposite direction and acceleration is found to be along F2 Find the forces F1 and F2.
Answer:
Consider the figure,
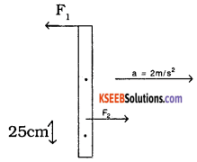
we know, Σ external = m acm
∴ F2 – F1 = 2(2) = 4N …………… (1)
also Σ τexternal = 1 αcm = 0 ( because there is no rotational motion)
∴ F2(0.25) = F1 (2) ……….. (2)
⇒ F2 = 8F1
∴ Substituting in (1)
8F1 – F1 = 4 N
⇒ F1 = \(\frac{4}{7}\) N
and F2 = 8 F1 = \(\frac{32}{7}\) N
Question 30.
A solid cylinder of mass M and radius R is held at rest in a horizontal position. Two strings are wound around the cylinder. As the string gets unwound, find tension in the string and acceleration of the cylinder.
Answer:
Consider the figure
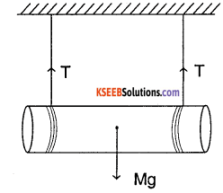
Let T be the tension in both strings. As the cylinder roTls down, a (linear acceleration)
= R α (angular acceleration) …………. (1)
also Σ Fext = macm = ma
∴ Mg – 2T = Ma …………….. (2)
also Στext = l α = \(\frac{M R^{2}}{2}\) α
⇒ 2TR = \(\frac{M R^{2}}{2}\) α
⇒ T = \(\frac{M R^{2}}{4}\) α ……………..(3)
From (1 ) and (3)
T = \(\frac{\mathrm{Ma}}{4}\)
⇒ Mg \(2\left(\frac{\mathrm{Ma}}{4}\right)\) = Ma (from (2))
⇒ Mg = \(\frac{3 \mathrm{Ma}}{4}\)
∴ a = \(\frac{2 g}{3}\) = 6.53 m/s²
and T = \(\frac{\mathrm{Ma}}{4}=\frac{\mathrm{M}}{4} \times \frac{2 \mathrm{g}}{3}=\frac{\mathrm{Mg}}{6}\)
Question 31.
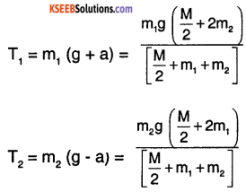
A pulley of the radius R and mass M has an Inextensible string placed over it. two masses M1 and M2 (M2 > M1) are attached to the free ends of the string. Find
- The acceleration of masses the system
- Tension in the string.
Answer:
Consider the free body diagram (FBD)
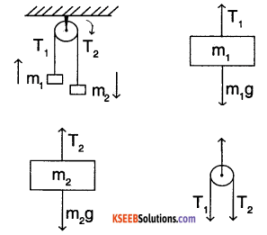
T1 and T2 are the tension at the two parts of the string N is normal force provided at the hinge.
considering equation ΣFext = ma
m2g – T2 = m2a ……….. (1)
m1g – T1 = m1a …………. (2)
[Since the 2 masses are connected by string they have same displacement hence same acceleration]
R αpulley = a – (3)
(condition for rolling of pulley)
(T2 – T1) R = l αpulley = \(\frac{M R^{2}}{2}\) αpulley ………. (4)
from (3) and (4)
T2 – T1 = \(\frac{\mathrm{Ma}}{2}\) ………….. (5)
from (1) and (2)
T2 = m2 (g – a)
and T1 = m1 (g + a)
∴ T2 – T1 = m2 (g – a) – m1 (g + a) = \(\frac{\mathrm{Ma}}{2}\)
⇒ g(m2 – m1) = a [\(\frac{M}{2}\) + m1 + m2]
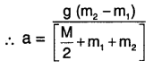
substituting a in (1) and (2)