You can Download Chapter 10 Mechanical Properties Of Fluids Questions and Answers, Notes, 1st PUC Physics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Physics Question Bank Chapter 10 Mechanical Properties Of Fluids
1st PUC Physics Mechanical Properties Of Fluids Textbook Questions and Answers
Question 1.
Explain why
1. The blood pressure In humans is greater at the feet than at the brain.
Answer:
The height of the blood column in the human body is more at the feet than at the brain. As the pressure increases with the height of the column, blood exerts more pressure at the feet than at the brain (P = ρgh)
2. Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km.
Answer:
The density of air is maximum near the surface of the earth (at sea level) and it decreases rapidly with height. The density of air at a height of 6 km reduces to almost half it’s value at sea level. Hence the atmospheric pressure at a height of 6 km decreases to nearly half of its value at sea level even though the height of the atmosphere is more than 100km.
3. Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.
Answer:
The pressure created while applying a force on a liquid is transmitted equally in all direction inside the liquid. That is why there is no fixed direction for the pressure transmitted. Hence we can say that hydrostatic pressure is a scalar quantity.
Question 2.
Explain why
1. The angle of contact of mercury with glass Is obtuse, while that of water with glass is acute.
Answer:
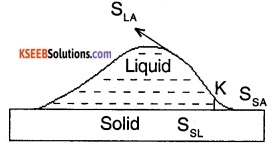
When a small quantity of liquid is poured on solid, three interfaces, namely liquid – air, solid – air, and solid-liquid are formed. The surface tension corresponding to theses three layers are SLA, SSA, and SSL respectively. Let θ be the angle of contact between the liquid and solid.
The molecules in the region, where the three interfaces meet is in equilibrium. It means that net force acting on them is zero. For the molecule at K to be in equilibrium, we have
SSL + SLA cos θ = SSA or cos θ = \(\frac{\mathrm{S}_{\mathrm{SA}}-\mathrm{S}_{\mathrm{SL}}}{\mathrm{S}_{\mathrm{LA}}}\) In case of mercury-glass, SSA < SSL, therefore cos θ is negative or θ > 90° i.e. (obtuse). In case of water-glass SSA > SSL, therefore cos θ is positive or θ < 90° (acute).
2. Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops.
Answer:
In the case of mercury the mercury glass, angle of contact is obtuse. To obtain this obtuse value of angle of contact, mercury tends to form a drop. But in the case of water, the water-glass angle of contact is acute. Thus the water tends to spread out to achieve this acute angle of contact.
3. The surface tension of a liquid is independent of the area of the surface.
Answer:
The surface tension of a liquid is the force acting per unit length on a line drawn tangentially to the liquid surface which is at rest. As this force is independent of the area of the liquid surface, the surface tension is also independent of the area of the liquid surface.
4. Water with detergent dissolved in ‘ it should have small angles of contact.
Answer:
The cloth has narrow spaces in the form of capillares. The rise of liquid in a capillary tube is directly proportional to cos θ. If θ is small cos θ will be large. Hence capillary rise will be more so that the detergent will penetrate more in cloth and hence gets dissolved.
5. A drop of liquid under no external forces is always spherical in shape.
Answer:
Is the absence of external forces, the surface of the liquid drop tends to acquire the minimum surface area due to surface tension. For a given volume, the surface area of the sphere is least and hence the liquid drop takes the spherical shapes.
![]()
Question 3.
Fill in the blanks using the word(s) from the list appended with each statement:
1. Surface tension of liquids generally …….with temperatures (increases /decreases)
Answer:
decreases
2. Viscosity of gases ……with temperature, whereas Viscosity of liquids …….with temperature (increases/decreases).
Answer:
increases, decreases
3. For solids with elastic modulus of rigidity, the shearing force is proportional to……, while for fluids it is proportional to …..(shear strain /rate of shear strain).
Answer:
Shear strain, rate of shear strain.
4. For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle).
Answer:
Both conservation of mass and Bernoulli’s principle.
5. For the model of a plane in a wind tunnel, turbulence occurs at a ….. speed for turbulence for an actual plane (greater / smaller).
Answer:
Greater
Question 4.
Explain why.
1. To keep a piece of paper horizontal, you should blow over, not under, it.
Answer:
If we blow over a piece, velocity of air above the paper becomes more than that below the paper. This reduces the pressure of the air above the paper in accordance with Bernoulli’s theorem. But the pressure of air below the paper is still atmospheric and is higher than the pressure above. Henc.e the paper remains horizontal and does not fall.
2. When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers.
Answer:
When we try to close the water top with our fingers, the area of outlet of water eject gets reduced. Therefore in accordance with the principle of Continuity (AV = constant), the velocity of the water will increase creating fast jets of water.
3. The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection.
Answer:
The size of the needle controls the velocity of flow and the thumb pressure controls the pressure. According to Bernoulli’s equation:
P + ρgh+ \(\frac{1}{2} \rho\) v2 = constant
we can note that the equation varies linearly with pressure, P but varies as the square of the velocity. Hence the contribution of velocity of flow is greater, due to which the needle has a better control over the flow.
4. A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel.
Answer:
When a fluid flows out of a small hole in a vessel, it acquires a large velocity and hence has a large momentum. Since no external force is acting on the system, a backward velocity must be acquired by the vessel (By-law of conservation of momentum). As a result backward thrust is experienced by the vessel.
5. A spinning cricket ball In air does not follow a parabolic trajectory.
Answer:
A spinning ball displaces air. The ball moves formed and relative to it, the air moves backward. Hence, the velocity of air above the ball relative to it is larger and below it is smaller. This difference in the velocities of air results in a pressure difference between the lower and upper faces leading to a net upward force on the ball. Therefore the ball does not follow a parabolic trajectory.
Question 5.
A 50 kg girl wearing high heel shoes balances on a single heel. The heel Is circular with a diameter of 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Answer:
Force exerted by the heel due to the weight of the girl, F = mg = 50 × 10 = 500N
Diameter of the heel’s circular are, d = 1 cm
= 10-2m
∴ Area of the heel \(\frac{\pi \mathrm{d}^{2}}{4}\)
= \(\frac{\pi \times\left(10^{-2}\right)^{2}}{4}=7.85 \times 10^{-5} \mathrm{m}^{2}\)
∴ Pressure exerted by the heel = \(\frac{F}{A}\)
\(=\frac{500}{7.85 \times 10^{-5}}\)
= 6.366 × 106 Pa.
![]()
Question 6.
Toricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m-3. Determine the height of the wine column for normal atmospheric pressure. (Assume g = 9.8 m/s2)
Answer:
Normal atmospheric pressure = 1 atm
⇒ gauge pressure of wine = 1 atm
ρgh = 1.013 × 105 Pa (Since 1 atm = 1.013 × 105pa)
⇒ h = \(\frac{1.013 \times 10^{5}}{984 \times 9.8}\)
⇒ h = 10.5 m.
Question 7.
A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.
Answer:
Maximum stress that can be taken by the off-share structure, Pmax = 109Pa.
density of water = 103 kg /m3 and g = 9.8 m/s2 and h = 3km (depth of the sea)
∴ Pressure exerted by seawater, P = ρgh
= 103 × 9.8 × 3 × 103
P = 2.94 × 107 Pa
Note that, P < Pmax
Since the pressure exerted by the seawater is less than the maximum pressure the structure can withstand, the structure is suitable for putting on the top of the oil well.
Question 8.
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000kg. The area of cross¬section of the piston carrying the load is 425 cm2. What maximum pressure would the smaller piston have to bear.
Answer:
Let Fmax be the maximum force experienced by the Bigger piston.
Fmax = mg = 3000 × 9.8 = 29400 N
Area of the bigger piston = 425 cm2
= 425 x 10-4m2
Maximum pressure on the bigger piston
pmax = \(\frac{F_{\max }}{A}\)
\(P=\frac{29400}{425 \times 10^{-4}}\) = 6.92 × 105 Pa
Since pressure is transmitted uniformly throughout the liquid the smaller piston will also bear a pressure of 6.92 × 105Pa.
Question 9.
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are In level with 10.0 cm of water in one arm and 12.5 cm of spirit In the other. What is the specific gravity of spirit?
Answer:
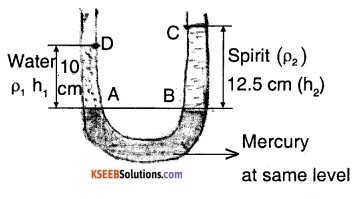
\(\rho_{1}\) → density of water
\(\rho_{2}\) → density of spirit
h1 → height of water column
h2 → height of spirit column
Let Po be the atmospheric pressure
⇒ PA = Po + \(\rho_{1}\) gh1 ….(1)
PB = Po + \(\rho_{2}\) gh2 …..(2)
Since the mercury levels are same at point A and B we can say that,
PA = PB
⇒ Po + \(\rho_{1}\) gh1 = Po + \(\rho_{2}\) gh2
from (1) and (2)
⇒ \(\rho_{1}\) gh1 = \(\rho_{2}\) gh2
⇒ \(\frac{\rho_{2}}{\rho_{1}}=\frac{h_{1}}{h_{2}}=\frac{10}{12.5}=0.8\)
∴ specific gravity of spirit
\(=\frac{\text { density of spirit }}{\text { density of water }}=\frac{\rho_{2}}{\rho_{1}}=0.8\)
Question 10.
In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms ? (Specific gravity of mercury = 13.6)
Answer:
Since we are putting equal amount of water and spirit and specific gravity of spirit is < 1 we can assume that the mercury level will rise on the spirit side,
\(\rho_{1}\) → density of water,
\(\rho_{2}\) → density of spirit,
\(\rho_{3}\) → density of mecury,
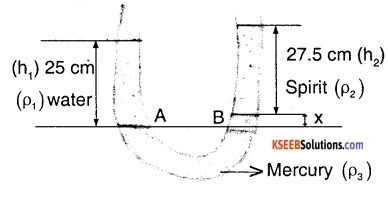
Since A and B are at the same height,
PA = PB
we know that, PA = \(\rho_{1}\)gh1
and PB = \(\rho_{2}\) gh2 + \(\rho_{3}\) gx
⇒ \(\rho_{1}\) gh1 = \(\rho_{2}\) gh2 + \(\rho_{3}\) gx
⇒ x = \(\frac{\rho_{1} h_{1}-\rho_{2} h_{2}}{\rho_{3}}\)
x = \(\frac{\mathrm{h}_{1}-\frac{\rho_{2}}{\rho_{1}} \mathrm{h}_{2}}{\frac{\rho_{3}}{\rho_{1}}}\)
where \(\frac{\rho_{2}}{\rho_{1}}\) ⇒ specific gravity of spirit and \(\frac{\rho_{3}}{\rho_{1}}\) ⇒ specific gravity of mercury.
Thus x = \(\frac{25-0.8 \times 27.5}{13.6}\) = 0.221 cm
Therefore the difference in the mercury level in the arms is 0.221 cm.
Question 11.
Can Bernoulli’s equation be used to describe the flow of water through a rapid in a river? Explain.
Answer:
No. The flow of water through a rapid in a river is turbulent and hence Bernoulli’s principle cannot be applied.
![]()
Question 12.
Does it matter if one uses gauge Instead of absolute pressures in applying Bernoulli’s equation? Explain.
Answer:
No, unless the atmospheric pressure at the two points where Bernoulli’s equation is applied are significantly different.
Question 13.
Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1cm. If the amount of glycerine collected per second at one end is 4.0 x 10-3 kg s-1, what is the pressure difference between the two ends of the tube? (Density of glycerine = 1.3 x 103 kg m-3 and viscosity of glycerine = 0.83 Pas). [You may also like to check if the assumption of laminar flow in the tube is correct].
Answer:
The volume of liquid floawing out per second is given by, \(Q=\frac{\pi R^{4}\left(p_{1}-p_{2}\right)}{8 h l}\)
⇒ pressure difference at tube ends, \(\mathrm{P}_{1}-\mathrm{P}_{2}=\frac{8 \mathrm{Q} \eta}{\pi \mathrm{r}^{4}}\)
where Q is the volume of liquid flowing per second = \(\frac{\text { mass of liquid flowing per second }}{\text { density of liquid }}\)
\(=\frac{4 \times 10^{-3} \mathrm{kg} / \mathrm{s}}{1.3 \times 10^{3} \mathrm{kg} / \mathrm{m}^{3}}\)
= 3.077 x 10-6 m3/s
Therefore,
P1 – P2 = \(=\frac{8 \times 0.83 \times 1.5 \times 3.077 \times 10^{-6}}{3.14 \times(1 \times 10)^{3}}\)
= 9.76 x 102 N/m2
A pressure difference of 9.76x 102 N/m2 is obtained.
Reynolds Number,
R = \(\frac{4 \rho V}{\pi d n}\) = \(\frac{4 \times 1.3 \times 10^{3} \times 3.08 \times 10^{-6}}{\pi \times(0.02) \times 0.83}\) = 0.3
Since the Reynolds number is about 0.3, the flaw is laminar.
Question 14.
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s-1 and 63 m s-1 respectively. What is the lift on the wing if its area is 2.5 m2? Take the density of air to be 1.3 kg m-3.
Answer:
P1 = pressure at the lower surface of wings
P2 = pressure at the lower surface of wings
ρ = Density of air
V1 = Speed of wind at the lower surface
= 63 m/s.
V2 = speed of wind at upper surface
= 70 m/s
According to Bermolli’s theorem,
P1 + \(\frac{1}{2} \rho V_{1}^{2}\) = P2 + \(\frac{1}{2} \rho V_{2}^{2}\)
or P1 – P2 = \(\frac{1}{2} \rho\left(V_{1}^{2}-V_{2}^{2}\right)\)
P1 – p2 = \(\frac{1}{2}\) × 1.3 × (702 – 632) = 605.15 pa
Force on wings = (P1 – P2) × area
= 605.15 × 2.5 = 1512.87 N
∴ The lift on the wings is about 1.512 × 103N
Question 15.
Figures 10.23(a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect? Why?
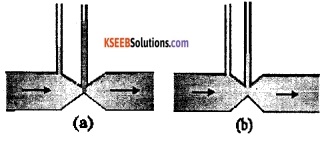
Answer:
Figure (a) is incorrect. From the equation of continuity AV = constant. Thus, when the area of constriction is narrow, velocity of streamline is high. If the velocity is high, we can say that the pressure head is low at that point (from Bernoulli’s equation). Correspondingly the height of the liquid column should be lesser at the narrow construction than that of the wide construction. Hence figure (a) is incorrect.
Question 16.
The cylindrical tube of a spray pump has a cross-section of 8.0 cm2 one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the. tube is 1.5 m min-1, what is the speed of ejection of the liquid through the holes?
Answer:
Number of holes = 40
Diameter of each hole, D = 10-3m
Area of cross section of each hole
\(=\frac{\pi D^{2}}{4}\)
\(=\frac{\pi \times 10^{-6}}{4}\)
Total area of cross section of 40 holes,
a2 = \(\frac{40 \times \pi \times 10^{-6}}{4}\) = π × 10-5m2
speed of liquid inside the tube,
V1 = 1.5 m/min = \(\frac{1.5}{60}\) m/s
Area of cross section of tube,
a1 = 8.0cm2 = 8 × 10-4m2
If V2 is the velocity of ejection of liquid through the holes then from equation of
continuity,
a1 v1 = a2 v2
⇒ v2 = \(\frac{a_{1} v_{1}}{a_{2}}=\frac{8 \times 10^{-4} \times 1.5}{60 \times \pi \times 10.5}\)
⇒ v2 = 0.637 m/s
∴ the speed of ejection is 0.637 m/s.
![]()
Question 17.
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 x 10-2N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
Answer:
The soap film has two free surfaces.
∴ Total length of the film to he supported,
l = 2 × 30 = 60 cm = 0.6
Total force on the slider due to surface tension will be, F = S × 2l = S × 0.6N
At equilibrium , the force F on slider due to surface tension should balance the weight mg
∴ F = mg = 1.5 × 10-2 N
⇒ S × 0.6 = 1.5 × 10-2
⇒ S = 2.5 × 10-2 N/m.
Question 18.
Figure 10.24 (a) shows a thin liquid film supporting a small weight = 4.5 × 10-2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
Answer:
In all three figures, the liquid is at the same. Temperature is also the same for each case. Hence, the surface tension in figure (b) and (c) is the same as in figure.
1. Since the length of the film in all the cases is 40 cm, the weight supported in each case is 4.5 × 10-2 N.
Question 19.
What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature? The surface tension of mercury at that temperature (20 °C) is 4.65 × 10-1 N m-1. The atmospheric pressure is 1.01 × 105 Pa. Also, give the excess pressure inside the drop.
Answer:
Radius of the mercury drop,
r = 3mm = 3 × 10-3m Surface tension of mercury, S = 4.65 × 10-1 Nm-1. Atmospheric pressure, Po = 1.01 × 105 Pa
Total pressure inside the mercury drop = Excess pressure inside mercury + Atmospheric pressure
= \(\frac{2 \mathrm{S}}{\mathrm{r}}\) + Po
= \(\frac{2 \times 4.65 \times 10^{-1}}{3 \times 10^{-3}}\) + 1.01 × 105
Total Pressure = 1.013 × 105 Pa
Excess pressure = \(\frac{2 \mathrm{S}}{\mathrm{r}}\)
\(=\frac{2 \times 4.65 \times 10^{-1}}{3 \times 10^{-3}}\)
= 310 Pa.
Question 20.
What is the excess pressure inside a bubble of soap solution of radius 5 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10-2 N/m? If an air bubble of the same dimension were formed at a depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
Answer:
Radius of the soap bubble, r = 5mm
= 5 × 103m
Surface tension of the soap solution,
S = 2.5 × 10-2 N/m
Since the soap Bubble has two surfaces,
Excess pressure, P = \(\frac{4 \mathrm{S}}{\mathrm{r}}\)
\(=\frac{4 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}\)
P = 20 Pa
Excess pressure inside the soap bubble is 20 Pa
Radius of air bubble, r = 5 mm = 5 × 10-3
Depth, h = 40 c = 0.4 m
Density of soap solution, ρ = 1.2 × 10-3 kg/m2
Atmospheric pressure, Po = 1.01 × 105 Pa
g = 9.8 m/s2
Excess pressure inside air bubble,
P1 = \(\frac{25}{r}\)
⇒ P1 = \(\frac{2 \times 2.5 \times 10^{-2}}{5 \times 10^{-3}}\)
P1 = 10Pa
At a depth of 0.4m, the total pressure inside the air bubble,
PTotal = Po + ρgh + P1
PTotal = 1.01 × 105 + 1.2 × 103 × 9.8 × 0.4 + 10
⇒ PTotal = 1.057 × 105Pa
∴ The pressure inside the air bubble is 1.06 × 105Pa.
Question 21.
A tank with a square base of area 1.0 m2 is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20 cm2. The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to a height of 4 m. compute the force necessary to keep the door closed.
Answer:
Assume g = 9.8 m/s2
Density of water, \(\rho_{1}\) = 103 kg/m3
height of water column, h1 = 4m
∴ Pressure due to water, P1 = \(\rho_{1}\) gh1
= 103 × 9.8 × 4
= 3.92 × 104 Pa
Density of acid
= Relative, densityx density of water = 1.7 × 103 kg/m3
height of acid column, h2 = 4m
∴ Pressure due to acid, P2 = \(\rho_{2}\) gh2
= 1.7 × 103 × 9.8 × 4
⇒ P2 = 6.664 × 104Pa
Pressure difference between the water and acid columns :
∆ P = P2 – P1
∆ P = 6.664 × 104 – 3.92 × 104
⇒ ∆ P = 2.744 × 104 Pa
Area of the door, a = 20 cm2
= 20 × 10-4m2
∴ Force exerted on the door, F = ∆ P × a
⇒ F = 2.744 × 104 × 20 × 10-4
F = 54.88 N
Therefore, the force necessary to keep the door closed is 54.88 N.
Question 22.
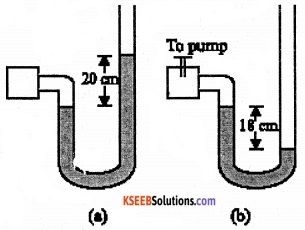
A manometer reads the pressure of a gas in an enclosure as shown in Fig. 10.25 (a) When a pump removes some of the gas, the manometer reads as in Fig. 10.25 (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury,
- Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), In units of cm of mercury.
- How would the levels change in case of (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).
Answer:
1. Difference between the mercury levels in the two limbs gives gauge pressure
∴ Gauge pressure, Pa = 20 cm of mercury
Atmospheric pressure, Po = 76 cm of mercury
∴ Absolute pressure = Atmospheric pressure + Gauge pressure
= 76 cm + 20 cm
= 96 cm of mercury
2. Difference between the levels of mercury in the two limbs = – 18 cm
∴ Gauge pressure = – 18cm of mercury
∴ Absolute pressure = Atmospheric pressure + Gauge pressure
= 76cm – 18 cm
= 58 cm of mercury.
Question 23.
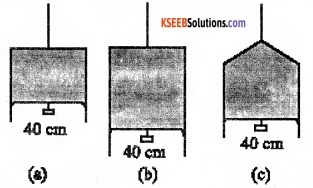
Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill up to a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?
Answer:
Two vessels having water-filled up to the same height, exert equal pressure on their bases. Also since the base area is the same, they exert an equal amount of force on the base. (F = PA). Force exerted on the sides of the vessels have non zero vertical components. When there vertical components are added, the total force experienced by one vessel will be different than the other vessel depending on the shape of the vessels. That is why the two vessels filled with water to the same vertical height show different readings on a weighing machine.
![]()
Question 24.
During a blood transfusion, the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein?
Answer:
Gauge pressure, P = 2000 Pa
Density of blood, ρ = 1.06 × 103 kg/m3
g = 9.8 m/s2
Let the height of the blood container be h
∴ pressure of the blood container, P = ρgh
⇒ ρgh = 2000
h = \(\frac{2000}{1.06 \times 10^{3} \times 9.8}\)
⇒ h = 0.1925 m
The blood may just enter the vein if the the blood container is kept at a height slightly greater than 0.1925 m.
Question 25.
In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy.
- What is the largest average velocity of blood flow in an artery of diameter 2 × 10-3 m if the flow must remain laminar?
- How does the pressure change as the fluid moves along the tube if dissipative forces are present?
- Do the dissipative forces become more important as the fluid velocity Increases? Discuss qualitatively.
Answer:
1. Diameter of artery = 2 × 10-3m
Viscosity of blood, = 2.084 × 10-3Pa s
Density of blood, ρ = 1.06 × 103kg/m3
Reynolds number for laminar flow,
NR = 2000
The largest average velocity of blood is
\(\mathrm{V}_{\mathrm{avg}}=\frac{\mathrm{N}_{\mathrm{R}} \eta}{\rho \mathrm{d}}\)
\(=\frac{2000 \times 2.084 \times 10^{-3}}{1.06 \times 10^{3} \times 2 \times 10^{-3}}\)
= 1.966 m/S
The largest average velocity of blood is 1.966 m/s.
2. If dissipative forces are present, then some forces in liquid flow due to pressure difference is spent against dissipative forces due to which the pressure drop becomes large.
3. The dissipative forces become more important with increasing flow velocity. This is because of the rise of turbulence. Turbulent flow causes dissipative losses in fluid.
Question 26.
- What is the largest average velocity of blood flow in an artery of radius 2 × 10-3m if the flow must remain laminar?
- What is the corresponding flow rate? (Take viscosity of blood to be 2.084 × 10-3 Pas).
Answer:
1. Diameter of artery, d = 2 × 2 × 10-3 m
= 4 × 10-3 m
Viscosity of blood, h = 2.084 × 10-3 m Pas
Density of blood, ρ = 1.06x 10-3 kg/m3
Reynold’s number for laminar flow,
NR = 2000
The largest average velocity of blood is,
\(\mathrm{V}_{\mathrm{avg}}=\frac{\mathrm{N}_{\mathrm{R}} \eta}{\rho \mathrm{d}}\)
\(V_{\text {avg }}=\frac{2000 \times 2.084 \times 10^{-3}}{1.06 \times 10^{3} \times 2 \times 10^{-3}}\)
V = 0.983 m/s
Hence, the largest average velocity of blood is 0.983 m/s.
2. Flow rate is given by
R= πr2Vavg
R = 3.14 × (2 × 10-3)2 × 0.983
⇒ R = 1.235 × 10-5m3/s
Therefore, the corresponding flow rate is 1.235 × 10-5m3/s
Question 27.
A plane is in level flight at constant speed and each of Its two wings has an area of 25 m2. If the speed of the air is 180 km/h over the lower wing and 234 km/h over the upper wing surface, determine the plane’s mass. (Take air density to be 1 kg m-3).
Answer:
Total area of wings, A = 2 × 25
= 50m2
speed of air lover the longer wing,
V1 = 180 km/h = 50 m/s
speed of air over the upper wings,
V2 = 243 km/h = 65 m/s
Density of air, ρ =1kg/m3
Let P1 and P2be the pressure of air over the lower wing and upper wing respectively.
From Bimoull’s equation,
P1 + \(\frac{1}{2} \rho V_{1}^{2}\) = P2 + \(\frac{1}{2} \rho V_{2}^{2}\)
P1 – P2 = \(\frac{1}{2} \rho\left(V_{2}^{2}-V_{1}^{2}\right)\)
∴ pressure difference, ∆ P
= \(\frac{1}{2} \rho\left(V_{2}^{2}-V_{1}^{2}\right)\)
= \(\frac{1}{2}\) × 1 × (652 – 502)
= 862.5 Pa
The upward force on the plane, F = ( ∆ P) A
= 862.5 × 50
=43125 N
We know that the upward force balances the weight of the plane
∴ F = mg
43125 = m × 9.8
⇒ m = 4400.51 kg.
Question 28.
In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 × 10-5 m and density 1.2 × 103 kg m-3? Take the viscosity of air at the temperature of the experiment to be 1.8 × 10-5 Pa s. How much is the viscous force on the drop at that speed? Neglect buoyancy of the drop due to air.(Take g = 9.8 ms2)
Answer:
Radius of the given unchanged drop, r = 2 × 10-5 m
Density of the uncharged drop,
ρ = 1.2 × 103 kg/m-3
Viscosity of air, \(\eta\) = 1.8 × 10-5 Pa S
The density of air (\(\rho_{0}\)) can be taken as zero in order to neglect the buoyancy of air.
Terminal velocity (v) is given by the relation:
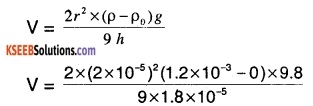
V = 5.807 × 10-2 m/s
V = 5.8 cm/s
The terminal speed of the drop is 5.8 cm/s
Viscous force, F = π 6 hrv
∴ F = 6 × 3.14 × 1.8 × 10-5 × 2 × 105 × 5.8 × 102
⇒ F = 3.9 × 10-10N
The viscous force on the drop is
= 3.9 × 10-10 N
Question 29.
Mercury has an angle of contact equal to 140° with soda-lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? The surface tension of mercury at the temperature of the experiment is 0.465 N m. Density of mercury = 13.6 × 103 kg m-3.
Answer:
Angle of contact 1 θ = 140°
Radius of the tube, r = 1 mm = 10-3m
Surface tepsion of mercury S = 0.465 N/m
Density of mercury, ρ = 13.6 × 103 kg/m3
g = 9.8 m/s2
Let the Dip in height of mercury be h Surface tension is given by,
S= \(\rho_{o} e^{-y / y_{o}}\)
⇒ h = \(\frac{2 \mathrm{S} \cos \theta}{\rho \mathrm{gr}}\)
⇒ h = \(\frac{2 \times 0.465 \times \cos 140^{\circ}}{13.6 \times 10^{3} \times 9.8 \times 10^{-3}}\)
h = – 0.00534 m = -5.34 mm
Negative sign indicates that mercury level, dips by 5.34 mm.
![]()
Question 30.
Two narrow bores of diameters 3.0 mm and 6.0 mm are Joined together to form a U-tube open at both ends. If the U-tube contains water, what Is the difference In its levels in the two limbs . of the tube? Surface tension of water at the temperature of the experiment is 7.3 × 10-2 N/m. Take the angle of contact to be zero and density of water to be 1.0 × 103 kg m-3 (g= 9.8 m s-2).
Answer:
Radius of the first bore, r1 = \(\frac{3 \mathrm{mm}}{2}\)
= 1.5 × 10-3 m
Radius of the second bore, r2 = \(\frac{6 \mathrm{mm}}{2}\)
= 3 × 10-3 m
Surface tension of water, S
= 7.3 × 10-2 N/m
Angle of contact, θ = 0°
(give in the question) Density of water, ρ = 1 × 103 kg/m3
Let h1 and h2 he the heights to which the water rises in the 3 mm and 6 mm diameter bores respectively.We have,
h1 = \(\frac{2 \mathrm{S} \cos \theta}{\mathrm{r}_{1} \rho \mathrm{g}}\)
h2 = \(\frac{2 \mathrm{S} \cos \dot{\theta}}{\mathrm{r}_{2} \rho \mathrm{g}}\)
Difference in water level = h1 – h2

= 4.966 × 10-3m
= 4.97 mm
The difference in the water levels in the cores is 4.97 mm.
Question 31.
1. It is known that density P of air decreases with height y as\(\rho_{\mathrm{o}} \mathrm{e}^{-y / \mathrm{y}_{0}}\) where \(\rho_{0}\) = 1.25 kg/m-3 is the density at sea level, and yo is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of the atmosphere remains a constant (isothermal conditions). Also, assume that the value of g remains constant.
2. A large He balloon of volume 1425 m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as It rises. How high does it rise?
[Take y0 = 8000m and \(\rho_{\mathrm{He}}\) = 0.18kg/m3].
Answer:
1. Volume of the balloon, V = 1425m3
Payload mass, m = 400 kg
g = 9.8 m/s2
Give that, yo = 8000m
\(\rho_{\mathrm{He}}\) =0.18 kg/m3
\(\rho_{\mathrm{o}}\) = 1.25 kg/m3
Density of the balloon = ρ
Let the height to which the balloon rises be y Density (ρ) of air decreases with height (y) as,
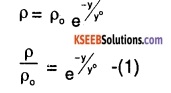
we can infer from (1), that rate of decrease of density with height is directly proportional to ρ,i.e.,

\(\frac{\mathrm{d} \rho}{\rho}=-\mathrm{kdy}\)
where, K is the constant of proportionality Height changes from o to y, while density changes from \(\rho_{\mathrm{o}}\)
to ρ by integrating.
we get:
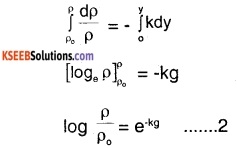
from (1) and (2),
yo = 1/K
⇒ K = \(\frac{1}{y_{0}}\)
From (2) and (3) we get,
![]()
2. Density,

⇒ ρ = 0.46 kg/m3
we have proved that,

⇒ y = – 8000 × loge \(\frac{0.46}{1.25}\)
⇒ y = 8000m = 8km .
Hence balloon will rise to a height of 8 km.
1st PUC Physics Mechanical Properties Of Fluids One Mark Questions and Answers
Question 1.
Pascal’s law is valid for dynamic fluids. True/False.
Answer:
False. Valid only for static fluid.
Question 2.
What is the relation between absolute pressure and gauge pressure?
Answer:
Absolute pressure = atmospheric pressure ± gauge pressure.
Question 3.
Angle of contact for a glass tube dipped in mercury is obtuse. True / False.
Answer:
True.
![]()
Question 4.
Water is an ideal fluid. True/False.
Answer:
False. It is real fluid.
Question 5.
Define thrust.
Answer:
The total normal force exerted by the fluid at rest on a surface is called thrust.
Question 6.
What is the dimensional formula for pressure?
Answer:
ML-1T-2
Question 7.
What happens to the viscosity of a gas when the temperature is increased?
Answer:
Viscosity of gases increases as the temperature is increased.
![]()
Question 8.
How does the coefficient of viscosity of liquid vary with temperature?
Answer:
The coefficient of viscosity of liquids decreases as temperature is increased.
1st PUC Physics Mechanical Properties Of Fluids Two Marks Questions and Answers
Question 1.
Name two applications of Pascal’s law.
Answer:
Hydraulic lifts, hydraulic breaks.
Question 2.
What is streamline? What are its properties?
Answer:
The path taken by a fluid particle under a steady flow is a streamline.
Properties:
- The tangent at any point in streamline gives direction of fluid velocity at that point.
- No two streamlines can cross.
Question 3.
Define the specific gravity of a fluid. What is its unit?
Answer:
Specific gravity is defined as a ratio of a density of a fluid to the density of water at 4°C. It has no unit.
Question 4.
Which are the factors on which viscous force depends?
Answer:
Viscous force acting between two layers of liquids depends on,
- area of the layers
- relative velocity of the two layers and
- distance between two layers.
![]()
Question 5.
A force 6f 1 kN is applied on a road surface by the tyre of a car. If the contact area of the tyre is 10 cm2, find the pressure on the contact area.
Answer:
Pressure = \(\frac{\text { Force }}{\text { area }}\)
\(\frac{1000 N}{10 \times 10^{-4} M^{2}}\) = 106 Pa
Question 6.
State whether true or false :
- An ideal liquid has non zero viscosity but zero compressibility.
- With increase in temperature, the viscosity of liquid decreases but the viscosity of gases increases.
Answer:
- False
- True.
Question 7.
A bigger raindrop falls faster than a smaller one (True/False) Explain.
Answer:
True.
The raindrop moves with terminal velocity due to viscous drag of the air. The terminal velocity of drop varies as the square of its radius. Hence, a bigger drop has a higher terminal velocity than a smaller one.
Question 8.
Machine parts get jammed during winter. Why?
Answer:
In winter, due to low temperature, the viscosity of oil between the machine parts increases considerably resulting in jamming of machine parts.
Question 9.
Discuss the effect of temperature on the viscosity of gases and liquids.
Answer:
Viscosity of liquid decreases with increase in temperature and viscosity of gases increases with increase in temperature.
Question 10.
What is an ideal liquid?
Answer:
- An ideal liquid is incompressible meaning density of liquid remains irrespective of the pressure.
- An ideal liquid is non-viscous. No tangential forces between layers of liquid in relative motion.
- Ideal liquid cannot withstand any shearing stress.
![]()
Question 11.
Explain the effect of density and pressure on the viscosity of liquids/gases.
Answer:
Liquids:
1. Viscosity increases with increase in density of the liquid. Viscosity increases with increase in pressure (except water).
2. Gases:
Viscosity decreases with increase in density. Viscosity decreases with increase in pressure.
Question 12.
The excess pressure inside a soap bubble is four times the excess pressure inside a moving soap bubble. What is the ratio of the first and second bubble?
Answer:
Let r1 and r2 be radius of soap bubbles. Excess pressure in them are
\(\frac{4 \sigma}{r_{1}}\) and \(\frac{4 \sigma}{r_{2}}\) where σ is surface tension.
Given P1 = 4P2 \(\frac{4 \sigma}{r_{1}}\) = 4 \(\frac{4 \sigma}{r_{2}}\)
ratio of volume of I to II
\(=\frac{r_{1}^{3}}{r_{2}^{3}}=\frac{r_{1}^{3}}{64 r_{1}^{3}}=\frac{1}{64}\)
Question 13.
Explain why water with detergent dissolved in it should have small angles of contact.
Answer:
Cloth has narrow spaces inform of capillaries. The rise of liquid in a capillary tube is directly proportional to cos e.
θ ∝ \(\frac{1}{\cos \theta}\). Hence e should be less in order that detergent penetrates more in clothes.
Question 14.
What is a venturi meter? Name two applications.
Answer:
Venturi meter is a device to measure the flow speed of incompressible fluid. The principle is used in filter pumps, Bunsen burner, atomiser.
Question 15.
Water is filled as shown In following containers. In which case highest force is exerted on the base of the container? Why?
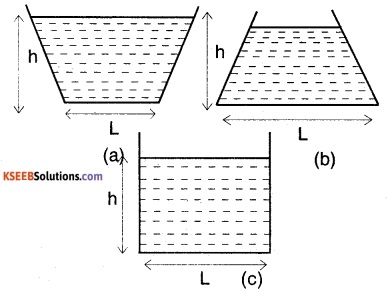
Answer:
Water exerts same pressure at the bottom of the container, regardless of its shape. Since height, his constant, equal pressure is exerted.
P = ρgh (h = constant)
Question 16.
Is it better to wash clothes in hot soap solution? Why?
Answer:
Yes. Surface tension decreases with temperature. Hence, in hot soap solution, spreading of solution over the surface of clothes happens easily. Hot soap solution can penetrate and clean clothes better.
Question 17.
Explain why a drop of liquid under no external force is always spherical in shape.
Answer:
Due to surface tension, a drop of liquid tries to acquire a shape with minimum surface area. For a given volume, surface area of sphere is least. Hence, liquid drop takes a spherical shape.
Question 18.
Point out any two properties required for a fluid to be used in a barometer.
Answer:
- Density of fluid should be high so as to avoid use of long barometer,
- Temperature variation of fluid should be minirial.
![]()
Question 19.
Why does water flow faster that honey?
Answer:
The coefficient of viscosity of water is less compared to that of honey. This makes water to move faster.
Question 20.
What are the factors affecting viscosity?
Answer:
- Increase in temperature decreases viscosity.
- Increases in pressure increases viscosity in liquids. In water, it decreases whereas, in gases, it remains the same.
Question 21.
What do you mean by angle of contact of a liquid with a solid surface. What are the factors that effect it?
Answer:
The angle made by the tangent drawn to the meniscus from the point of contact with the walls of the container measured from within the liquid is called angle of contact. It depends on the atmosphere pressure, adhesive and cohesive forces of the liquid in the tube.
Question 22.
Bernoulli’s equation can be used to describe the flow of a river rapidly. True/False. Explain why?
Answer:
False. Bernoulli’s equation can be applied only to streamline flow.
Question 23.
Archimedes’s Principle holds good in a vessel at free fall. True/False. Give reason.
Answer:
False
The principle does not hold good in this particular case as the vessel in free fall is in a condition of weightlessness, where the buoyant force accounting for the Archimedes’s principle does not exist.
Question 24.
Why are cars and aeroplanes streamlined?
Answer:
The shape of the aeroplane is streamlined because when it flies in air. The velocity on the top surface is more than the bottom surface. Hence the pressure on the top surface decreases. This causes an upward thrust on the wings of the place which gives uplift to the aeroplane.
Question 25
Why do some liquids rise and some liquids dip in a capillary tube? Explain
Answer:
The rise or fall of liquid in a capillary tube is due to surface tension. If the liquid wets the glass then there is rise in the liquid inside the capillary tube.
![]()
Question 26.
Define cohesive force and adhesive, force of molecules.
Answer:
Force of attraction between molecules of the same substance is called cohesive force. Force of attraction between molecules of the different substances is called adhesive force.
Question 27.
Diameter of a ball A is thrice that of B. What will be the ratio of their terminal velocities in water?
Answer:
Terminal velocity × (rad. of ball)2 Required ratio is \(\frac{3^{2}}{1}\) = 9
Question 28.
A hole of area 2 mm opens near bottom of a large water storage tank and stream of water shoots from it. If top of the water in the tank is to be kept 30 m above leaking point, how much water in litres Is should be added to reservoir tank to keep this level? Take g = 10 m/s2
Answer:
Velocity of the outflowing water
v = \(\sqrt{2 g h}=\sqrt{2 \times 10 \times 30}\) = 24.49 m/s
Quantity of water flowing out per sec.
= av = 10-5 × 4 × 24.49
= 97.96 × 10-6
= 9.796 × 10-5 × 103 litres/s
= 97.96 ml/s.
Question 29.
A small ball of mass m and density ρ is dropped in a viscous liquid having density \(\rho_{0}\). After some time, ball falls with a constant velocity. Calculate viscous force acting on the ball.
Answer:
Volume of the ball, v = m/ρ; mass of liquid displaced by the ball.
\(\mathrm{m}^{\prime}=\left(\frac{\mathrm{m}}{\rho}\right) \rho_{0}\)
ρ = density of ball
When the ball falls with a constant velocity
⇒ viscous force = effective weight of the ball or F = mg = m’g = (m – m’)g
\(=\left(\mathrm{m}-\frac{\mathrm{m} \rho_{0}}{\rho}\right) \mathrm{g}=\mathrm{mg}\left(1-\frac{\rho_{0}}{\rho}\right)\)
Question 30.
What is Reynold’s number? What is its significance?
Answer:
Turbulent flow is less likely for viscous fluid flowing at low rates. A dimensionless number, whose value gives one an approximate idea whether the flow would be turbulent. This number is called the Reynold’s Re.
\(R_{e}=\rho v d / \eta\)
ρ → density of fluid
speed v,d stands for the dimension of the pipe.
\(\eta\) → viscosity of the fluid. Significance is that,
flow is lamina’s/streamline for Re <1000 flow is turbulent for Re > 2000.
Question 31.
A wooden log 100 mm × 100 mm × 5 m hangs vertically from a vertical string so that 3 m length of log Is submerged in water. Find the tension in string. Take specific gravity of wood = 0.65.
Answer:
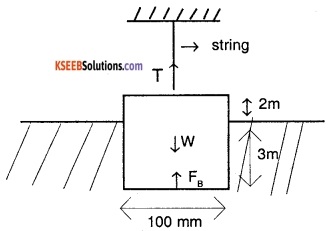
FB + T = W
(0.1 × 0.1 × 3) × 9810 + T
= (0.1 × 0.1 × 5) × 0.65 × 9810
T = 24.52 N
(0.1 × 0.1 × 3) × 9810 + T
= (0.1 × 0.1 × 5) × 0.65 × 9810
∴ T = 24.52 N
Question 32.
A piston of small cross-section A1 is used to exert a force F1 on liquid to transfer it from the existing cylinder to a larger cylinder attached with a larger piston of area A2. What is the weight, say if a truck that can be placed on a platform supported by the larger piston due to the force exerted on the liquid in existing cylinder?
Answer:
F2 = \(\frac{\mathrm{F}_{1} \mathrm{A}_{2}}{\mathrm{A}_{1}}=\frac{100 \mathrm{kN} \times 1 \mathrm{m}^{2}}{10 \times 10^{-4} \mathrm{m}^{2}}\)
= 105 kN
∴ Weight of truck = 105 kN.
![]()
Question 33.
The pressure inside a droplet of water is 10.3 N/m2 in excess of atmospheric pressure. Its diameter is 50 mm. Find surface tension of the water film.
Answer:
P = \(\frac{2 \lambda}{r}\)
λ = \(\frac{P r}{2}=\frac{10.3 \times 25 \times 10^{3}}{2}\)
= 128.75 N/m
1st PUC Physics Mechanical Properties Of Fluids Four/Five Marks Questions and Answers
Question 1.
Define viscosity. Discuss the cause the viscosity.
Answer:
Viscosity is the property of a fluid, (liquid or gas) by virtue of which an internal frictional force comes into play when the fluid is in motion and opposes the relative motion of its different layers. Viscosity is due to the intermolecular forces which are effective when the different layers of the liquid are moving with different velocities.
These forces are of Vander waal type. Due to these forces, every fast-moving liquid layers tends to accelerate the adjoining slow-moving layers and every slow-moving layer tends to retard the adjoining fast-moving layer of liquid. As a result a backward dragging force called viscous drag comes into play which accounts for viscosity of liquid.
Question 2.
Derive the dimensional formula for co-efficient of viscosity and hence its unit.
Answer:
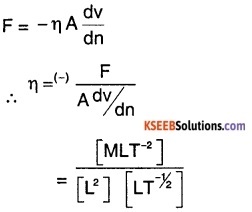
Units:
We have \(\eta=\frac{F}{A d v / d n}\)
in cgs system, the unit of \(\eta\) is called poise.
1 poise \(=\frac{1 \mathrm{dyne}}{1 \mathrm{cm}^{2} \times(1(\mathrm{cm} / \mathrm{s}) / \mathrm{cm})}\)
= dyne cm-2 sec.
The S.I.unit of \(\eta\) is Pa.s (Pascal second) or deca poise.
1 dec poise = \(\frac{1 \mathrm{N}}{1 \mathrm{m}^{2}\left(1 \mathrm{ms}^{-1} / \mathrm{m}\right)}\) = 1Nsm-2
Question 3.
State Stoke’s law? What are the factors on which viscous drag depends?
Answer:
Stoke’s law states the backward dragging force (F) acting on a small spherical body of radius r, moving through a medium having coefficient of viscosity \(\eta\) and velocity v is given by
F = 6π\(\eta\)rv
viscous drag (F) depends on
- coefficient of viscosity of the medium \(\eta\)
- velocity of the body (v)
- radius of the spherical body (r)
Question 4.
How is the rise of liquid affected if top of the capillary is closed?
Answer:
There will be a small rise in the capillary tube if top of capillary tube is closed. Because the rise of liquid in capillary tube due to surface tension will be opposed by the downward force exerted by the compressed air above the liquid in tube. This downward force increases with increase in height of liquid column. Therefore only a small rise of liquid column is possible in a capillary tube with a closed top.
Question 5.
What is terminal velocity? What are the factors on which terminal velocity depends?
Answer:
The terminal velocity of an object is the maximum constant velocity acquired by the object while falling freely in a viscous medium.
Terminal velocity (v) of an object of radius (r) density \((\rho)\) moving through a viscous medius of viscosity \(\eta\) and density \(\rho_{0}\) is given by
\(\mathrm{v}=\frac{2}{9} \frac{\mathrm{r}^{2}}{\eta}\left(\rho-\rho_{0}\right) \mathrm{g}\)
Hence, terminal velocity depends on
- radius of the object
- coefficient of viscosity of the medium
- density of the object.
- density of the medium
Question 6.
Derive expression for capillary rise in a tube in terms of surface tension, radius of tube angle of contact and density of fluid.
Answer:
Consider a tube of radius ‘a’ dipped in a container filled with fluid of density of ρ as shown.
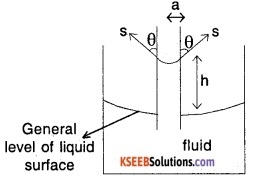
h = capillary rise
s = surface tension
θ = angle of contact
a = radius of tube
The weight of column of liquid of height h in the tube is balanced by vertical component of the surface tensile force of fluid. Vertical component of the surface tensile force
= (S cos θ) × (length over which it acts)
= (S cos θ) × circumference of tube
= S cos θ × 2πa ……..(1)
Weight of column of fluid balanced by surface tension = volume of fluid × density × g
= (πa2h) × ρg ……(2)
Equating (1)and(2),
S cosθ × 2πa = πa2h ρg
h \(=\frac{S \cos \theta \times 2}{a \rho g}\)
\(=\frac{2 \mathrm{S} \cos \theta}{\mathrm{a} \rho \mathrm{g}}\)
Question 7.
State and prove the Archimedes principle?
Answer:
Archimedes principle states that when a body is wholly partially immersed in a liquid at rest. The loss of weight of the body in the liquid is equal to the weight of the liquid displaced by the immersed part of the body.
Proof:
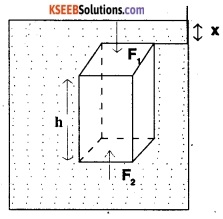
Let A be the cross-sectional area of the top or bottom face of the object.
Volume of liquid displaced, v = volume of the object = Ah
∴ mass of liquid displaced, m = vρ = Ahρ
ρ is the density of the liquid.
Liquid pressure on the top of the body
P1 = xρg
Vertical downward thrust (Force f1) on top face of the object.
F1 = P1A = xgAρ
Liquid pressure on the bottom face of body P2 = (x + h) ρg
Vertical upward thrust (Force F2) on bottom force
F2 = P2 A(X + h) ρgA.
Since F2 >F1, the net upward force acting is F = F2 – F = (x + h) ρ gA – x ρgA
= hρgA = hA(ρg)
= mg
weight of liquid displaced.
True weight of the object = Mg
Upward thrust (Force F) on the body F = mg
Apparent weight of the body in liquid.
= W-F = Mg – mg
This means that observed weight at the body (object) immersed in a liquid is less than its true weight by an amount equal to weight of the liquid displaced by body.
Question 8.
State and prove Bernoulli’s theorem.
Answer:
Bernoulli theorem states that for streamlined flow of an ideal liquid, the total energy (Pressure energy + potential energy + kinetic energy) per unit mass remains constant at every cross-section throughout the flow.
Proof:
Consider a tube AB of varying cross-section through which an ideal liquid is in streamlined flow.

Let P1 be the pressure applied on the liquid at A and P2 be the pressure against which liquid has to move out at B
a1, a2 be the cross-sectional area at tube at A and B
h1 and h2 are the mean height at section A and B from the reference level.
v1 and v2 are the velocity of liquid flow at A and B
ρ is the density of the ideal liquid flowing through the tube.
The liquid flows from A to B hence,
P1 > P2
The mass m of the liquid crossing per second through any section at the tube with respect to equation of continuity is,
a1v1 ρ = a2v2 = ρm
a1v1 = a2v2 = V (say)
Force on liquid at A = P1a1
Force on liquid at B = P2a2
Work done per second by liquid at A = P1a1 × v1 = P1V
Work done per second by liquid at B = P2a2 × v2 = P2V
Net work done per second on liquid by pressure energy moving from A to B is
= P1V- P2V = v (P1-P2)
Increase in potential energy per second as the liquid flows from A to B
= mgh2 – mgh,
(since v2 is greater than v1)
Increase in kinetic energy per second of liquid from A to B = 1/2 m\(v_{2}^{2}\) – 1/2 m\(v_{1}^{2}\)
According to work – energy principle, work done per second by pressure energy
= increase in P.E per second + increase in K.E per second
or P1v – P2v = (mgh2 – mgh1) + \(\left(\frac{1}{2} m v_{2}^{2}-\frac{1}{2} m v_{1}^{2}\right)\)
i.e., P1v + mgh1 + \(\frac{1}{2} m v_{1}^{2}\)
= P2v + mgh2 + \(\frac{1}{2} m v_{2}^{2}\)
Dividing by m1
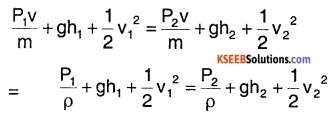
Hence, \(\frac{\mathrm{P}}{\rho}+\mathrm{gh}+\frac{1}{2} \mathrm{v}^{2}\) = constant.
But, \(\frac{P}{\rho}\) is the pressure energy per unit mass, gh is the potential energy per unit mass and \(\frac{1}{2} v^{2}\) is the kinetic energy
per unit mass Hence,
Pressure Energy + Potential Energy + Kinetic Energy remains constant.
Hence proved.
Question 9.
Derive the equation at continuity.
Answer:
Consider a non-viscous liquid in streamlined flow through a tube AB at varying cross-section.
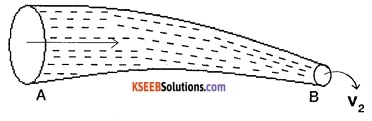
Let a1, a2 be the area of cross-section of the tube at A and B.
v1, v2 = velocity of flow of liquid at A and B.
Volume of the liuid entering per second at A = a1v1
Mass of liquid entering per second at A = a1v1\(\rho_{1}\)
Similarly mass of liquid leaving per second at B = a2v2 \(\rho_{2}\)
Assuming, no loss of liquid in the tube and
steady flow, then mass of liquid entering at A/sec = mass of liquid leaving at B/sec.
⇒ a1v1\(\rho_{1}\) = a2v2\(\rho_{2}\)
Assuming liquid is incompressible,
\(\rho_{1}\) = \(\rho_{2}\)
⇒ a1v1 = a2v2
av = constant
This is the equation of continuity.
![]()
Question 10.
Explain the limitations of Bernoulli theorem.
Answer:
- While deriving the Bernoulli theorem, it is assumed that the velocity of every particle of liquid across any crosssection is uniform. Practically this is not possible.
- Viscous drag of the liquid which comes into play when the liquid is in motion has not been considered.
- While deriving the equation, it is assumed that there is no loss of energy when liquid is in motion. In fact, some KE is converted to heat energy.
- If a liquid is flowing along a curved path, energy due to centrifugal force should also be considered.
Question 11.
Explain why the angle of contact of water with glass is acute while that mercury with glass is obtuse?
Answer:
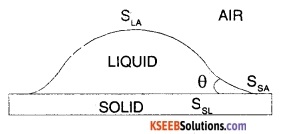
SSL + SLA cos θ = SSA
or cos θ = \(\frac{S_{S A}-S_{S L}}{S_{L A}}\)
In case of mercury – glass, SSA < SSL
∴ cos θ is negative or θ>90° i.e., obtuse.
In case of water – glass, SSA > SSL
cos θ is positive or θ<90° i.e., acute.
Note:
SSL:
Surface tension corresponding to solid-liquid interface.
SLA:
Surface tension corresponding to liquid – air interface.
SSA:
Surface tension corresponding to solid-air interface.
Question 12.
Derive an expression for velocity of fluid at wide neck in a venturi meter.
Answer:
Speed of fluid flowing through tube at broad neck = V1
Speed of fluid flowing through tube at narrow neck = V2
By equation of continuity,
A1V1 = A2V2
V2 = \(\frac{A_{1} V_{1}}{A_{2}}=\frac{A V_{1}}{a}\)
From Bernoulli’s equation,

Question 13.
What is the Magnus effect? Explain.
Answer:
A ball Which is spinning drags air along with it. If the surface is rough, more air will be dragged.
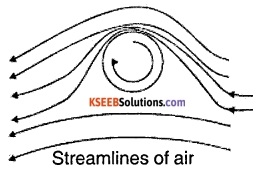
Ball is moving forward and relative to it air is moving backwards. This results in a larger velocity of air relative to the ball above it and a smaller velocity below it. This difference in velocities of air results in pressure difference between lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spinning is called the Magnus effect.
Question 14.
Define terminal velocity. Give reasons why a sphere attains this velocity. Derive a relation for the terminal velocity.
Answer:
The constant velocity with which a body drops down after initial acceleration in a dense liquid or fluid is called terminal velocity. This is attained when the apparent weight is compensated by the viscous force. It is given by
v = \(\frac{2}{9} \frac{r^{2} g}{\eta}(\rho-\sigma)\), where ρ and σ are densities of the body and liquid respectively, \(\eta\) is the coefficient of viscosity of liquid and r is the radius of the spherical body.
The net force on the sphere becomes zero as the viscous force equals the apparent weight.
Consider a long column of dense liquid-like glycerine. As the ball is dropped in it, the forces experienced are;
- weight = mg = \(\frac{4}{3} \pi r^{3} \rho g\), where ρ is the density of the ball.
- upthrust = U = \(\frac{4}{3} \pi r^{3} \rho_{1} g\), where\(\rho_{1}\) is the density of the liquid.
- viscous force Fv = \(6 \pi \eta \rho v\), where v is the terminal velocity.
Net force and the acceleration should be 0.
∴ mg – U – Fv = 0

Question 15.
Write the differences between laminas/streamline flow and turbulent flow.
Answer:
1. Laminar Flow
- Layered flow with one layer of fluid sliding smoothly over the other.
- Reynold’s No. < 1000
- Observed usually in flow through porous materials.
2. Turbulent
- Haphazard flow with rapid and continuous mixing of fluid resulting in momentum transfer.
- Reynold’s No. > 2000
- Pipeline flow, river flow, etc.
![]()
Question 16.
A razor blade can be made to float on water. What forces act on this blade? Is Archimedes’s principle applicable?
Answer:
Three forces are acting on the blade when it is made to float on water:
- Weight of blade acting vertically downwards.
- Reaction in blade exerted by the liquid surface acting vertically upwards.
- Force of surface tension on circumference, of the blade acting tangentially to the liquid surface.
In this case, as no portion of razor blade is immersed in water, hence Archimedes’s principle is not applicable.
1st PUC Physics Mechanical Properties Of Fluids Numerical Problems Questions and Answers
Question 1.
A capillary tube of diameter 1.5 mm is dipped in
- mercury.
- water.
Find capillary rise for each case. Surface tension for water and mercury can be taken as 0.07 N/m and 0.52 N/m respectively. The contact angle for water and mercury can be taken as 0° and 130°.
Answer:
1. h = \(\frac{4 \lambda \cos \theta}{\mathrm{dr}}\)
\(=\frac{4 \times 0.52 \times \cos (130)}{1.5 \times 10^{-3} \times 13.65 \times 9810}\)
= 6.66 mm (fall)
2. h = \(\frac{4 \lambda \cos \theta}{\mathrm{dr}}\)
\(=\frac{4 \times 0.07 \times 1}{1.5 \times 10^{-3} \times 9810}\)
= 19 mm (rise).
Question 2.
Calculate the energy evolved when 8 droplets of water (surface tension 0.72 N/m) of radius 0.5 mm combine into one.
Answer:
Here, s = 0.072 N/m
r = 0.5 mm = 0.5 × 10-3 m.
Let R be the radius of big drop formed.
Volume of the big drop = volume of 8 small drops.
\(\frac{4}{3}\) π R3 = 8 × \(\frac{4}{3}\) πr3
or R = 2 r = 2 × 0.5 × 10-3= 10-3 m
Surface area of big drop :
= 4π R2 = 4π × (10-3)2
= 4π × 10-6m2
Surface area of 8 small drops:
= 8 × 4π × r2
= 8 × 4π × (0.5 × 10-3)2
= 8π × 10-6m2
Energy evolved = S.T × decrease in area.
= 0.072 × 4π × 10-6 = 9.05 × 107J.
![]()
Question 3.
A plate 0.025 mm distant from a fixed plate moves at 60 cm/s and requires a force of 2 N per meter square to maintain its speed. Determine fluid viscosity between the plates.
Answer:
dy = 0.025 mm
= 0.025 × 10-3m
Velocity of upper plate .
= 60 cm/s = 0.6 m/s
Force on upper plate
= 2\(\frac{\mathrm{N}}{\mathrm{m}^{2}}\) = Shear stress , τ
du = change of velocity = u – 0 = 0.6 m/s
dy = change of distance = 0.025 × 10-3m
Viscosity,
µ = \(\frac{\tau}{\mathrm{du} / \mathrm{dy}}=\frac{2}{\left(0.6 / 0.25 \times 10^{-3}\right)}\)
8.33 × 10-5 \(\frac{\mathrm{Ns}}{\mathrm{m}^{2}}\) = 8.33 × 10-5 Pas
Question 4.
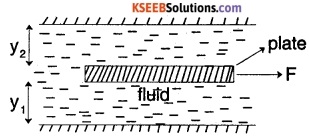
In the above figure, if area of plate is A, viscosity of fluid is µ, distance of plate from top and bottom plane surfaces are y1 and y2 respectively, find the expression for force F required to drag the plate at a velocity v.
Answer:
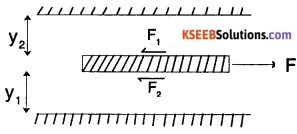
Required force F = F1 + F2
\(=\frac{\mu_{1} A_{1} v_{1}}{y_{1}}+\frac{\mu_{2} A_{2} v_{2}}{y_{2}}\)
\(=\mu \mathrm{Av}\left(\frac{1}{\mathrm{y}_{1}}+\frac{1}{\mathrm{y}_{2}}\right)\)
Question 5.
An open tank contains water up to a depth of 3m and above it an oil of sp.gr 0.9 for a depth of 1m. Find pressure intensity
- at the interface of two liquids
- at the bottom of the tank.
Answer:
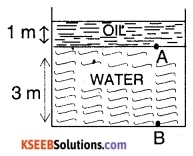
Height of water, z1 = 3 m
Height of oil, z2 = 1 m
Density of oil
= Sp.gr of oil × Density of water
= 0.9 × 1000 kg/m3 = 9000 kg/m3
= \(\rho_{2}\)
Density of water = \(\rho_{1}\) = 1000 kg/m3
1. At the interface, i.e., at A,
P= \(\rho_{2}\) g × z2 = 900 × 9.81 × 1
= 8829 N/m2
2. At the bottom i.e., at B,
p =\(\rho_{2}\)gz2 + \(\rho_{1}\)gz1
= 900 × 9.81 × 1 + 1000 × 9.81 × 3
= 8829 + 29430 = 38259 N/m2
Question 6.
Determine pressure difference between two points A and B for the setup as shown in figure.
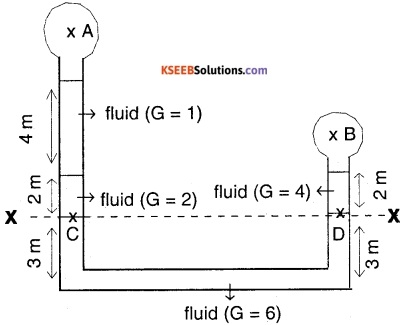
Answer:
G = specific gravity,
PA = pressure at A,
PB = Pressure at B
Pressure at any point is the same horizontal line x – x should be same.
Hence, pressure at C in left column = pressure at D in right column.
Pressure at C
= (2 × 1000 × g × 2) + (1 × 1000 × g × 4) + PA …..(1)
pressure at D
= (4 × 1000 × g × 2) + PB ……(2)
Equating (1) and (2),
8000 g + PA = 8000 g + PB
PA – PB = 0
Question 7.
A closed tank contains 1m of mercury, 2m of water and 3 m of oil of sp.gravity 0.6. There is an unknown fluid in space above oil. If gauge pressure at the bottom of the tank is 200 kPa. What is the pressure on the top surface of oil?
Answer:
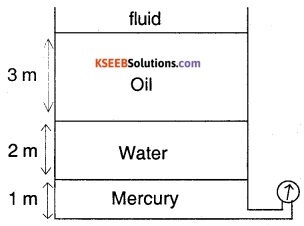
Let pressure on top of oil be PA
Total pressure = PA + Poil +Pwater + Pmercury
P= ρgh
200 × 103 =PA + 0.6 × 1000 × g × 3 + 1000 × g × 2 + 13.6 × 1000 × g × 1
PA = 200 × 103 – 170694
= 29.306 kPa
Question 8.
The flow rate of water from a tap of diameter 1.2 cm is 0.48 L/min. The coefficient of viscosity of H20 is 10-3 Pa s. After some time the flow rate is increased to 4 L/min. Characterise the flow for both the flow rates.
Answer:
Let the speed of the flow be v and the area of tap be d = 1.2 cm. The volume of the water flowing out per second is
Q = v × πd2 /4
v = 4Q/d2
Reynold’s number is
Re = 4P2 / πd\(\eta\)
= 4 × 103kg/m3× Q/(3.14 × 1.2 × 10-2m × 10-1Pa s)
= 1.061 × 108 m-3s Q = 1.061 × 108Q
Initially,
Q = 0.48 L/min = 8.0 cm3/s
= 8.00 × 10-6m3/s
we obtain
R =484.8
Since this is below 1000, the flow is steady.
After sometime when Q = 4L/min,
= 66.67 cm3/s
= 6.67 × 10-5 m3s-1
we obtain
R = 1.061 × 108 × 6.67 × 10-5
= 7076.9
The flow now is turbulent.
![]()
Question 9.
Calculate the total energy possessed by one kg of water at a point where pressure is 30 gm wt/sq.mm. Velocity of 0.1 ms-1 and height is 60 cm above the ground.
Answer:
Given, P = 30 g wt/sq.mm
= \(\frac{30}{1000}\) × 9.8 × 106N/m2
v = 0.1ms-1 h = 0.6 m
Total energy per unit mass
\(\frac{P}{\rho}\) + gh + 1/2 v2
= \(\frac{30 \times 9.8 \times 10^{3}}{10^{3}}\) + 9.8 × 0.6 + 1/2 × (0.1)2
= 294 + 5.88 + 0.005
= 299.885 J.
Question 10.
Water flows at the rate of 4 litres per second through an orifice at the bottom of the tank which contains water 720 cm deep. Find the rate of escape of water If additional pressure of 20 kg/cm2 is applied to the surface of water.
Answer:
Given, h = 720 cm v = \(\sqrt{2 g h}\)
v = \(\sqrt{2 \times 980 \times 720}\) cm/s ;
= 1187.93 cm/s v
v = 4 litres
Additional pressure = 20 kg/cm2
= 20000 g/cm2
\(\frac{20000 \times 980}{980}\) Cm 0f Water
= 20,000 cm of water column.
Now, pressure head (h1) = 20,000 + 720
= 20,720 cm
New velocity v1 = \(\sqrt{2 \mathrm{gh}_{1}}\)
\(\sqrt{2 \times 980 \times 20,720}\) cm/s
= 6372.69 cm/s
As v = av and V1 = av1
v1 = V\(\frac{v_{1}}{v}\) = 4 × \(\sqrt{\frac{20720}{720}}\)
= 21.45 litres/s
Question 11.
A venturi meter is connected to two points in the mains where its radii are 20 cm and 10 cm. and the levels of water column in the tubes differ by 10 cms. How much water flows through the pipe per minute?
Answer:
Volume of water flowing per second
v = a1a2\(\sqrt{\frac{2 g h}{a_{1}^{2}-a_{2}^{2}}}\)
where a1 = \(\pi r_{1}^{2}\) = 22/2 × 2012cm2
a2 = \(\pi r_{2}^{2}\) 22/7 × 1012cm2
g = 980 cm/s2;
h = 10 cm .
Volume of water flowing per minute
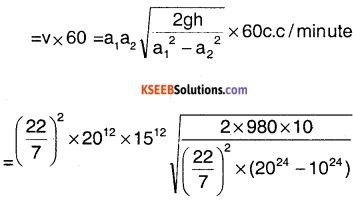
= 2726.58 litres/minute.
Question 12.
When a drop of mercury of radius R is split into n similar drops, What is the change in surface energy? Assume σ as surface tension of mercury.
Answer:
Volume of initial mercury drop = \(\frac{4}{3}\) πR3
r = radius of smaller drops,
volume conservation
⇒ \(\frac{4}{3}\) πR3 = n \(\frac{4}{3}\) πr3
r = Rn-1/3
Initial Surface Energy = σ × surface area
= σ × 4πR2
Final Surface Energy = n × σ × 4πr2
= nσ 4π[Rn-1/3]2
= nσ 4πR2n-2/3
= n1/34σ πR2
Change in surface energy
= 4σ πR2[1 – n1/3]
Question 13.
- The diameter of pipe at section (1) and (2) are 10 and 15 cm respectively. Find discharge through pipe if the velocity of water flowing through pipe at section (1) is 5 m/s. Find also velocity at section (2)
- Find the work done in blowing a soup bubble of surface tension 0.06 N/m from a 2 cm radius to a 5 cm radius.
Answer:
1.
Q = A1V1 = π × \(\frac{0.1^{2}}{4}\) × 5
= 0.0393 m3/s
V2 = \(\frac{A_{1} V_{1}}{A_{2}}\) (continuity equation)
= \(\frac{0.0393}{\frac{\pi}{4} \times 0.15^{2}}\) = 2.22 m/s
2. Here, s = 0.06 N/m
r1 = 2 cm = 0.02 m ;
r2 = 5 cm = 0.05 m
Since bubble has 2 surfaces, initial surface area of the bubble.
= 2 × 4πr12= 2 × 4π(0.02)2
= 32π × 10-4m2
Final surface area of the bubble
= 2 × 4πr22 = 2 × 4π(0.05)2
= 200π × 10-4m2
Increase in surface area
= 200π × 10-4 – 32π × 10-4
= 168π × 10-4m2
∴ work done = S × increase in surface area
= 0.06 × 168π × 10-4 = 0.003168 J
Question 14.
A tank is filled with water to a height H. At a depth ‘h’ from the free surface a hole is made so that the water comes out of it. What is the velocity of efflux? Also, what is the maximum range and the position of hole for the same? Find the time taken by a water molecule to reach the ground. Determine the horizontal length covered by the molecule.
Answer:
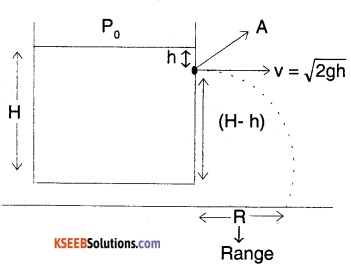
Take two points at the same height (H- h) from ground one inside and one outside the hole. Applying Bernoulli’s theorem for the points, we have
\(\frac{P_{0}+h p g}{\rho g}\) + 0 + (H – h) = (H – h) + \(\frac{v^{2}}{2 g}+\frac{P_{0}}{\rho g}\)
On Solving, we get, v = \(\sqrt{2 \mathrm{gh}}\)
The velocity of efflux thus depends on the depth of which the hole is made from the surface of the liquid. Time taken to reach
ground = t = \(\sqrt{\frac{2(\mathrm{H}-\mathrm{h})}{\mathrm{g}}}\),
Since v = \(\sqrt{2 \mathrm{gh}}\) is horizontal and ax = 0;
R = vt = \(\sqrt{2 \mathrm{gh}}\) \(\sqrt{\frac{2(\mathrm{H}-\mathrm{h})}{\mathrm{g}}}\)
R = \(2 \sqrt{\mathrm{h}(\mathrm{H}-\mathrm{h})}\)
To maximise Range, \(\frac{\mathrm{d} \mathrm{R}}{\mathrm{dh}}\) = 0
i.e., h = H/2
Maximum Range,
\(R_{\max }=2 \sqrt{\frac{H}{2}(H-H / 2)}=H\).
![]()
Question 15.
Water flows through a horizontal pipe of varying cross-section. If the pressure is 1 cm of mercury when the velocity is 0.35 m/s. Find the pressure at a point where velocity is 0.65 m/s.
Answer:
At 1st point, P1 = 1 cm of mercury
= 0.01m of Hg.
= 0.01 × (13.6 × 103) × 9.8 P a;
v1 = 0.35 m/s
At the second nd point,
p2 = ?
v2 = 0.65 m/s and
ρ = 103 hg/m3.
According to Bernoulli’s theorem,
p1 + 1/2 \(\rho \mathrm{V}_{1}^{2}\) = p2 + 1/2 \(\rho \mathrm{V}_{2}^{2}\)
or P2 = P1 + 1/2 \(\rho\left(v_{2}^{2}-v_{1}^{2}\right)\)
= 0.01 × 13.6 × 103 × 9.8 – 1/2 × 103 × [(0.65)2 – (0.35)2]
= 1182.8 Pa ⇒ \(\frac{1182.8}{9.8\left(13.6 \times 10^{3}\right)}\)
= 0.00887 m of Hg.
Question 16.
If excess pressure inside a soap bubble of diameter 2 cm is balanced by that due to a column of oil of sp.gravity 0.8, 2mm high, find the surface tension of the soap bubble.
Answer:
R = 1 cm = 10-2 m
ρ of oil = 0.8 × 103kg/m3
h = 2 mm = 2 × 10-3m
Pressure due to 2 mm column of oil,
P = hρg – (2 × 10-3)(0.8 × 10-3) × 9.8
= 2 × 0.8 × 9.8 Pa
In case of soap bubble, P = \(\frac{4 \mathrm{s}}{r}\)
or s = \(\frac{P r}{4}=\frac{2 \times 0.8 \times 9.8 \times 10^{-2}}{4}\)
= 3.92 × 10-2N/m
Question 17.
A spray pump having a cylindrical tube of cross-section 8 cm2 has 50 fine holes of radius 0.5 mm. Consider the flow of liquid inside the tube to be 1.5 m/min. What is the speed of ejection of the liquid through the whole?
Answer:
Area of cross-section of the tube:
a1 = 8 cm2 = 8 × 10-4m2
Number of holes = 50
Diameter of each hole = 0.5 × 2 = 1 mm
= 10-3
or radius of the hole
= 0.5 mm = 5 × 10-4m
Area of cross-section of each hole
= π r2 = π (5 × 10-4)2 m2
Total area of cross-section of 50 holes,
a2= 50 × π(5 × 10-4) m2
Speed of the liquid inside the tube,
v1 = 1.5 m/min = \(\frac{1.5}{60}\) m/s
If v2 is the velocity of ejection of the liquid through the holes,
then, a1v1 = a2v2 or v2 = a1v1/a2
∴ v2 = \(\frac{\left(8 \times 10^{-4}\right) \times 1.5}{60 \times 50 \times \pi \times\left(5 \times 10^{-4}\right)^{2}}\)
= 0.5096 m/s.
![]()
Question 18.
Calculate the total energy/unit mass possessed by water at a point, where the pressures is 10gm f/sq mm, velocity is 0.1 m/s and height of water level from the ground is 0.2 m (g = 9.8 m/s2).
Answer:
Here, P = 10 gm f/sq mm
= \(\frac{10}{1000}\) × 9.8 × (103)2
= 98 × 103Nm-2
v = 0.1 m/s ;
ρ = 103 kg/m3;
h = 0.20 m
1. Pressure energy / unit mass
= \(\frac{P}{\rho}=\frac{9.8 \times 10^{3}}{10^{3}}\) = 98 J/kg
2. Gravitational potential energy / unit mass = gh = 9.8 × 0.2 = 1.96 J/kg
3. Kinetic energy / unit mass
= 1/2 v2= \(\frac{1}{2}\)(0.1)2 = 0.0053/kg
∴ Total energy / unit mass
= \(\frac{P}{\rho}\) + gh + 1/2 v2 = 98 + 1.96 + 0.005
= 99.965 J/kg
Question 19.
A mass of 15 kg is placed on the wider tube of a U tube as shown in the figure. Given that the area of the wider tube is 5 m2, find the difference in the water levels in the two tubes, (density of water = 1 kg/m3).
Answer:
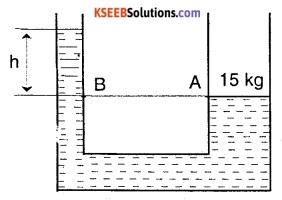
![]()
Area of the wider tube, A = 500 cm2
= 5 × 10-2 m2
The pressure applied by the mass at A is transmitted through the liquid and leads to a difference in the water levels.
Since the water level is same a A and B,
PA = PB ……(1)
But PA = \(\frac{F}{A}=\frac{m g}{A}=\frac{15 \times 9.8}{5}\) = 29.4 Pa
Also we know that PB = ρgh = 1 × 9.8 × h
From (1) PB = PA
9.8 × h = 29.4
h = 3m
∴ The difference in water level obtained is 3 m.
Question 20.
If two liquids of mass m1 and m2 and density \(\rho_{1}\), and \(\rho_{2}\) are mixed together, then what is the density of the resulting mixture?
Answer:
Volume occupied by first liquid,
V1 = \(\frac{m_{1}}{\rho_{1}}\)
Volume occupied by second liquid,
V2 = \(\frac{m_{2}}{\rho_{2}}\)
∴ density of the mixture,
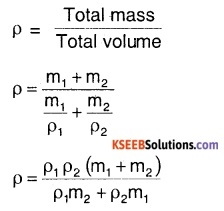
Question 21.
The container shown in the figure below is filled with a liquid of density ρ. Note that the container has a height h1 and area of cross-section A1 for the upper half height h2 and area of cross-section A2 for the lower half. Find:
- The pressure at the base of the container.
- Force exerted by the liquid on the base of the container.
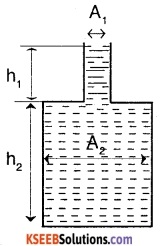
Answer:
1. The pressure at the base of the container is due to the liquids both at the upper and lower half.
∴ PTotal = P1 + P2
PTotal = ρgh1 + ρgh2
PTotal = ρg(h1 + h2)
2. Force exerted on the bottom of the container,
P = PTotal × A2
F = ρg(h1 + h2) × A2.