Students can Download 1st PUC Physics Model Question Paper 4 with Answers, Karnataka 1st PUC Physics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Physics Model Question Paper 4 with Answers
Time: 3.15 Hours
Max Marks: 70
General Instructions:
- All parts are compulsory.
- Draw relevant figure / diagram wherever necessary.
- Numerical problems should be solved with relevant formulae.
Part – A
I. Answer the following questions: ( 10 × 1 = 10)
Question 1.
Name the experiment which established the nuclear model of atom.
Answer:
Geiger-Marsdon experiment on alpha-particle scattering by gold foil.
Question 2.
What is S.I. unit of luminous intensity?
Answer:
The SI unit luminous intensity is candela (cd).
Question 3.
Give an example for two dimensional motion.
Answer:
Projectile motion and circular motion.
Question 4.
Why don’t action and reaction forces cancel each other?
Answer:
Action and reaction forces act on two interacting bodies, so the forces don’t cancel each other.
![]()
Question 5.
A light body and a heavy body have the same momentum. Which one will have greater kinetic energy?
Answer:
Since K.E. ∝ \(\frac{1}{m}\) for same linear momentum, lighter body has more kinetic energy.
Question 6.
Give the expression for moment of inertia of a circular disc of radius R about its diameter.
Answer:
I = \(\frac{M R^{2}}{4}\)
Question 7.
What are geostationary satellites?
Answer:
Geo-stationary satellites orbit around the Earth with the speed of the satellite equal to the rotational speed of the Earth. Hence, these satellites appear to be fixed with respect to a place on the surface of the Earth.
Question 8.
What is shear deformation?
Answer:
Shear deformation is the ratio of lateral displacement of one edge to the vertical distance between the opposite faces of the body.
Question 9.
How does melting point of ice changes with increase of pressure?
Answer:
The ice will go to a lower melting point.
![]()
Question 10.
Give an example for a wave which can travel through vacuum.
Answer:
Electromagnetic wave.
Part – B
II. Answer any FIVE of the following questions: ( 5 × 2 = 10 )
Question 11.
Given the relative error in the measurement of the radius of a circle is 0.02, whal is the percentage error in the measurement of its area?
Answer:
A = πr2
\(\frac{\Delta \mathrm{A}}{\mathrm{A}}=2 \mathrm{r} \frac{\Delta r}{r}\)
= 2 × r × 0.02 = 0.04r
(\(\frac{\Delta \mathrm{A}}{\mathrm{A}}\)) = 0.04r
Question 12.
What are the significance of velocity – time graph?
Answer:
The slope of the line on a v-t graph gives the acceleration of the particle.
Question 13.
What is resolution of a vector? What is the x-component of a vector A, that makes an angle 300 with x-axis.
Answer:
A single vector can be resolved in two or more number of directions each of which is known as the component of a vector. This splitting is known as resolution of vector.
\(\overrightarrow{\mathrm{A}}_{x}=\left(A \cos 30^{\circ} \hat{i}\right)=\frac{\sqrt{3}}{2} \hat{i}\)
![]()
Question 14.
Give the general conditions of equilibrium of a rigid body.
Answer:
(1) The vector sum of the forces on the rigid body is zero for translatory equilibrium
\(\sum_{i=1}^{n} \vec{F}_{i}=0\) and (acceleration a = 0 )
(2) The vector sum of the torques on the rigid body is zero for rotatory equilibrium (a=0) i.e.
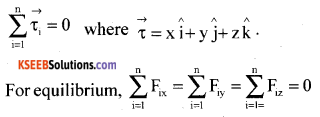
i.e., the components of X, Y, and Z independently vanish to zero for linear equilibrium.
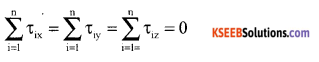
Sum of X components, Y components and Z components of torque on the particles, vanish for rotational equilibrium.
Question 15.
Write Stoke’s formula for viscous drag force. Explain the terms.
Answer:
F = 6πηav where v – terminal speed of liquid, η – coefficient of viscosity, a – radius of the spherical object and F – viscous drag force.
Question 16.
What is meant by anomalous behavior of water. What is its significance?
Answer:
The density of water increases from 0°C to 4°C and thereafter decreases with increase of temperature.
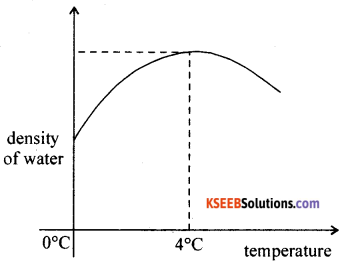
This behaviour of water from 0°C to 4°C is known as anomalous expansion of water. Water at 4°C has the maximum density and sinks down. However, water below the surface, relatively having lower density, rises above. Water becomes lighter as the temperature falls below 4°C. Ice at 0°C has the minimum density and floats on water. Hence marine animals can survive below ice. It is water everywhere below ice.
![]()
Question 17.
State and explain first law of thermodynamics.
Answer:
The energy (∆Q) supplied to the system goes in partly to increase the internal energy of the system (∆U) and the rest in doing work on the environment (∆W).
∆Q = ∆U + ∆W
where ∆Q → heat supplied, ∆U → change in internal energy, ∆W → work done
Question 18.
What is periodic motion. Give an example.
Answer:
A particle event that repeats itself in regular intervals of time is known as the periodic motion. Both circular and elliptical motions of electrons around the atomic nucleus are examples of periodic motions.
Part – C
III. Answer any FIVE of the following questions : ( 5 × 3 = 15 )
Question 19.
Derive the expression for time of flight of a projectile.
Answer:
Expression for time of flight:
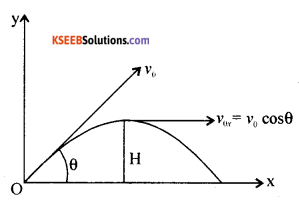
Consider v = (v0 sinθ) – gt
Put v = 0, fort = time of ascent = ta
ta = \(\frac{v_{0} \sin \theta}{g}\)
but time of ascent = time of descent
and time of flight T = ta + td
i.e., T = \(\frac{2 v_{0} \sin \theta}{g}\) and T ∝ v0 for a given angle of projection.
![]()
Question 20.
Arrive at the statement of principle of conservation of linear momentum from Newton’s laws of motion.
Answer:
Statement: In an isolated system of collision of bodies, the total linear momentum before impact is equal to the total linear momentum after impact.

Let m1 and m2 be the masses of two bodies moving along \(\vec{v}_{1 i}\) and \(\vec{v}_{2 i}\). Let \(\vec{v}_{1 f}\) and be the \(\vec{v}_{2 f}\) be final velocities after the impact.
At the time of impact the force of action acts on the body B and the force of reaction acts on A.
Applying Newton’s III law of motion
\( |Force of action on \mathrm{B}|=-| Force of reaction on \mathrm{A} |\)
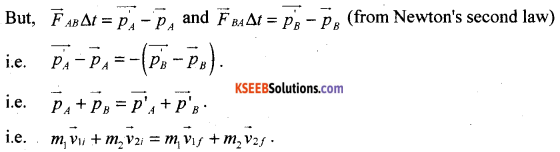
This shows that the total final linear momentum of the isolated system equals its total initial momentum.
Question 21.
Prove that potential energy stored in a spring is, where k is the force constant of the spring and x is the change in length Of the spring.
Answer:
Work done by the spring force = Ws= \(-\int_{0}^{x_{\mathrm{m}}} \mathrm{F}_{\mathrm{s}} \mathrm{d} \mathrm{x}\)
W = \(=-\int_{0}^{x_{m}} \mathrm{k} x \mathrm{d} \mathrm{x}\)
W = \(-\frac{1}{2} \mathrm{k} x_{\mathrm{m}}^{2}\)
Work done by the external pulling force = W= \(\frac{1}{2} \mathrm{k} x_{\mathrm{m}}^{2}\)
Question 22.
State Kepler’s laws of planetary motion.
Answer:
Kepler’s I law (Law of orbit): All planets revolve in elliptical orbits with Sun as one of its foci.
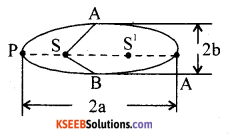
2a – Major axis length
2b – Minor axis length
S-Sun at one focus P
S1 – The other focus of the ellipse
P – Perihelion position of the planet.
A – Apehelion position of the planet.
Kepler’s II law (Law of areas) : The line joining the planet and the Sun sweeps out equal areas in equal intervals of time.
\(\frac{\Delta \overrightarrow{\mathrm{A}}}{\Delta \mathrm{t}}=\frac{1}{2 \mathrm{m}} \overrightarrow{\mathrm{L}}\)

Kepler’s III law (Law of periods) : The square of the period of revolution of a planet around the sun is directly proportional to the cube of the semi major axis of the ellipse.
i.e., T2 ∝ a3 so that for two planets
\(\left(\frac{T_{1}}{T_{2}}\right)^{2}=\left(\frac{a_{1}}{a_{2}}\right)^{3}\)
Question 23.
Prove that the centre of mass of a system moves with constant velocity in the absence of external force on the system.
Answer:
When there is no external force the acceleration of the body is zero.
Force = rate of change of momentum.

∴M is not zero
so this proves that velocity will always be constant in such scenario.
Question 24.
State and explain Hooke’s law. Define modulus of elasticity.
Answer:
Statement: The ratio of stress to strain is a constant for a material within the elastic limit.
Modulus of elasticity = \(\frac{\text { Stress }}{\text { Strain }}\)
Within the elastic limit, stress v/s strain is a straight line ‘A’ is the elastic limit upto which Hooke’s law is applicable. Beyond ‘B’ the yielding point, the wire extends but does not return to the initial state when the deforming force is removed. ‘F’ is the breaking point. ‘EF’ allows the material to be malleable and ‘DE’, ductile.
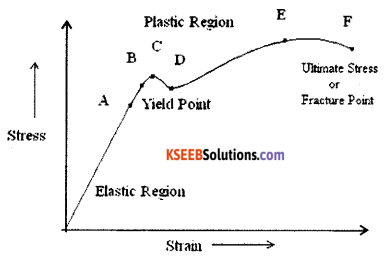
![]()
Question 25.
State Bernoulli’s theorem. What are its applications?
Answer:
Along a steamline, in a steady flow of non viscous fluid, potential energy, kinetic energy and pressure energy remain constant.
Applications
- Uplift of air craft and
- Atomisers work on the principle of Bernoulli’s theorem.
Question 26.
What is Doppler effect. Write any two applications of Doppler’s effect.
Answer:
The phenomenon of apparent change in frequency due to relative motion between the source of sound and the listener (observer) is known as Doppler effect.
Applications of Doppler effect:
- It is used in radar.
- It is used by meteorologists to track storms.
- Doppler effect of sound is used to diagnose heart problems in the hospital.
Part – D
IV. Answer any TWO of the following questions : ( 2 × 5 = 10 )
Question 27.
Find the magnitude and direction of the resultant of two vectors A and B in terms of their magnitudes and angle, between them.
Answer:
To find the magnitude of the resultant:
From the OAC, \(\vec{P}+\vec{Q}=\vec{R}\)
CD is ⊥r to OD. From the pythagoras theorem,
OC2 = OD2 + DC2 ……….(1)
but DC2 = AC2 + AD2 ……..(2)
From the right angled triangle ADC,
sinθ = CD/AC
∴AC sinθ = CD …….(3)
cosθ = AD /AC
ie., AD = AC cosθ ……..(4)
Eqn. (1) can be written as
OC2 = (OA + AD)2 + DC2
sin OC2 = OA2 + AD2 + 20A.AD + DC2
using (2) and (4) we get
OC2 = OA2 + AC2 + 20A. AC cosθ
i.e. R2 + P2 + Q2 + 2PQ cosθ
Hence, R = (P2 + Q2 + 2PQ cosθ)1/2
To find the direction of the resultant:
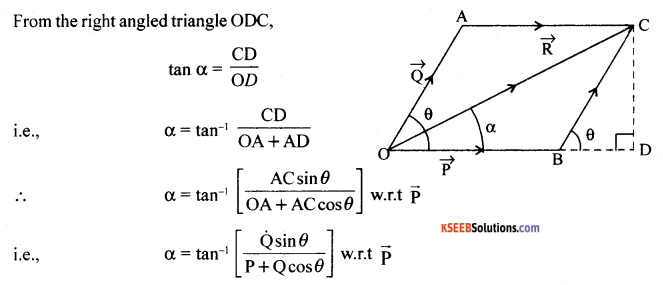
![]()
Question 28.
State Newton’s second law of motion and hence derive F= ma.
Answer:
Newton’s II law of motion:
Statement: “The rate of change in the linear momentum of a body is directly proportional to the impressed force and takes place in the direction of force applied.
To show that \(\vec{F}=m \vec{a}\).
Let m be the mass of the body. Let be the initial linear momentum. Let be the final linear momentum as a result of the impressed force.
By definition \(\lim _{\Delta t \rightarrow 0} \frac{\Delta \vec{p}}{\Delta t}=\frac{d \vec{p}}{d t}\) where \(\Delta \vec{p}=\vec{p}_{f}-\vec{p}_{i}\), and \(\frac{d \vec{p}}{d t}\) is instantaneous acceleration.
From Newton’s II law of motion,

But the magnitude of force \(|\overrightarrow{\mathrm{F}}|\) is so defined that k = 1 : We denote \(|\vec{F}|=m|\vec{a}|\)
Thus F=ma and \(\vec{F}=m \vec{a}\).
Question 29.
Define torque. Show that torque on a particle is equal to rate of change of its angular momentum.
Answer:
The rotating effect of force is called torque and is represented by \(\vec{\tau}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{F}}\).
i.e. t=rFsin8
where O is the angle between r and F.
Fora system of n particles,
Net angular momentum = \(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{L}_{1}}+\overrightarrow{\mathrm{L}_{2}}+\ldots \ldots . \overrightarrow{\mathrm{L}_{n}}=\sum \overrightarrow{\mathrm{r}_{1}} \times \overrightarrow{\mathrm{p}_{1}}\)
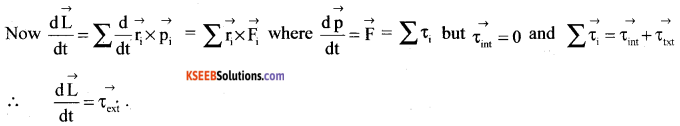
V. Answer any TWO of the following questions : ( 2 × 5 = 10 )
Question 30.
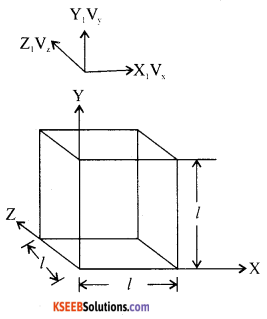
Using kinetic theory of gases derive an expression for finding the pressure of an ideal gas in terms of mean squared speeds of the molecules.
Answer:
Let an ideal gas be enclosed in a cubical vessel of side l. Area of cross wall will be A =l2. Let Vx be the velocity of the molecule hitting the plane of wall (of the vessel) YZ. After collision, it rebounds with the same speed but in the opposite direction along a straight line. The change in ‘ velocity of the molecule along the X direction is vx – (-vx) = 2vx.
The change in linear momentum imparted to the wall in the collision process = 2.mvx where m is the mass of the molecule.
But force exerted on the wall = rate of change in momentum = \(\frac{2 m v_{x}}{\Delta t}\)
Pressure exerted on the wall due to 1 molecule = \(\frac{\text { Force }}{\text { Area }}\)
∴Pressure due to single molecule = \(\frac{2 m v_{x}}{\left(A^{2}\right) \Delta t}\) where A = l2.
Total number of molecules hitting the wall and returning back = (Volume) (number density) Distance travelled by the molecule = (vx∆t)
Volume covered = (vx∆t)(A)
Total number of molecules hitting the wall on an average = \(\frac{1}{2}\) (vx∆tA)(n)
Hence pressure exerted on the wall = P
P = \(\left(\frac{2 m v_{x}}{A \Delta t}\right)\left(\frac{1}{2} v_{x} \Delta t A n\right)\)
i.e., P = mnvx2
By symmetry (isotropic condition of speed)
\(\overline{\mathbf{v}}_{x}^{2}=\overline{\mathbf{v}}_{y}^{2}=\overline{\mathbf{v}}_{z}^{2}\)
So, the mean of the squred speed along any one axis
= (\(\frac{1}{3}\)) \(\overline{\mathbf{v}^{2}}\)
Thus P = mn (\(\frac{1}{3}\)\(\overline{\mathbf{v}^{2}}\)).
i.e., P = \(\frac{1}{3}\)mn\(\overline{\mathbf{v}^{2}}\)
![]()
Question 31.
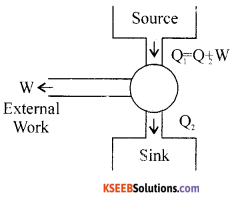
Describe Carnot’s cycle and write the expression for its efficiency.
Answer:
Working of Carnot’s engine:
Step 1 : The working substance (ideal gas) is enclosed ¡n a non-conducting wall and conducting bottom of a cylinder fitted with air tight non conducting piston. This is placed on the source having an infinite thermal capacity at a steady temperature.
The top surface is conducting and the rest non conducting. As a result, the gas expands isothermally. The work done
by the system.
Q = W1 = μRT1 log\(\frac{V_{2}}{V_{1}}\)(curve A B)
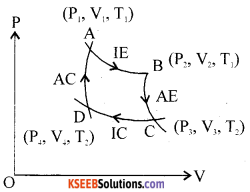
Step 2 : The working substance is now placed on a non L conducting platform. as a result ofwhich no heat exchange takes place between the system and the surroundings. [he system expands adiabatically at the expense of its internal energy. The gas cools. The work done by the system.
\(\mathrm{W}_{2}=\frac{\mu \mathrm{R}}{\gamma-1}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)\)(curve B C)
Step 3 : The working substance is now placed on the sink maintained at a steady low temperature T,K. The system undergoes isothermal compression at this temperature. The pressure of gas increases and volume decreases without any change in the internal energy and specific heat of gas remains at infinity.
\(\mathrm{W}_{3}=\mu \mathrm{RT}_{2} \log \left(\frac{\mathrm{V}_{4}}{\mathrm{V}_{3}}\right)\) (curve C D)
Step 4: The working substance is placed on a non-conducting platform, Under thermal isolation. the system undergoes change in its internal energy and its specific heat remains at zero. Adiabatic compression results in increase in the pressure and temperature at the expense of work being done on the system. The system is allowed to reach its initial slate. This completes one cycle of operation. The area hounded by the curves gives the amount of heat converted into work.
\(\mathrm{W}_{4}=\frac{-\mu \mathrm{R}}{\gamma-1}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)\) (curve D A)
i.e., Net work done = W =W1 + W2 +W3 + W4
Work done = μR(T – T2) \(\log _{e}\left(\frac{V_{2}}{V_{1}}\right)\)
∴Efficiency η = \(\frac{\mathrm{w}}{\mathrm{Q}}=1-\frac{\mathrm{T}_{2}}{\mathrm{T}_{1}}\)
Question 32.
Derive the Newton’s formula to find the speed of a longitudinal wave in an ideal gas. What is the Laplace correction to obtain the speed of sound in air?
Answer:
v = \(\sqrt{\frac{p}{\rho}}\) where ‘p’is pressure on gaseous medium. ρ – density of gaseous medium.
Consider adiabatic variation in the pressure and volume of gaseous medium.
PV = constant.
Since no change of heat takes place between the system and the surrounding.
A(PVγ) = 0
i.e., γPVγ-1 ∆V+Vγ ∆P = 0
i.e., Bulk modulus = \(-\frac{\Delta \mathrm{P}}{\frac{\Delta \mathrm{V}}{\mathrm{V}}}\) = γP
Hence in the expression V = \(\sqrt{\frac{\mathrm{E}}{\rho}}\), Elasticity ‘E is replaced by γP.
Laplace equation is written as v = \(=\sqrt{\frac{\gamma \mathrm{P}}{\rho}}\).
Where γ = 1 + 2/f and ‘f’ is number of degrees of freedom of gaseous molecule.
VI. Answer any THREE of the following questions : ( 3 × 5 = 15 )
Question 33.
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?
Answer:
The distance between two buses just when one takes is vT.
u = 20 km/hr
When they move in the same direction, relative velocity = v – u
The time to cover the distance,
t= 18 mm = \(\frac{18}{60}\)hrs
distance = t (v-u)
t (v-u) = vT
vT = \(\frac{3}{10}\)(v-u)……..(1)
When they move in the opposite direction, relative velocity = v + u
∴Time to cover the distance, t = 6 minutes = \(\frac{6}{60}\)hrs
∴t (v + u) = vT
vT = \(\frac{1}{10}\)(v + u)……..(2)
Equating vT from the eqn (1) and (2)
\(\frac{3}{10}\)(v-u) = \(\frac{1}{10}\)(v + u)
3v – 3u = v + u
∴v = 2u
v = 40 km/hr …….(3)
Substituting in eqn (2)
40 xT = \(\frac{1}{10}\)(40 + 20)
T = \(\frac{3}{20}\)hrs
T = 9 minutes.
![]()
Question 34.
A person trying to lose weight(dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 in each time. Assume that the potential energy lost each time she lowers the mass is dissipated, (a) How much work does she do against the gravitational force? (b) Fat supplies 3.8 × 107 J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?
Answer:
Given m = 10 kg, g = 9.8 ms-2 , h = 0.5m, n = 1000
Energy supplied by fat is 3.8 × 107 J /kg, efficiency = 20%
∴20 % of energy supplied by fat = 3.8 × 107 × 0.20 = 0.76 × 10-7 Jkg-1
Work done against the gravity = n mgh =103 × 10 × 9.8 × 0.5 = 4.9 × 104J
Mass of fat used = \(\frac{4.9 \times 10^{4}}{0.76 \times 10^{7}}\) = 6.45 × 10-3 kg
Question 35.
Phobos is a satellite of the planet mars. Phobos has a period 7 hours, 39 minutes and an orbital radius of 9.4 × 103 km. calculate the mass of mars. Assume that earth and mars move in circular orbits around the sun, with martian orbit being 1.52 times the orbital radius of earth. What 1 the length of the martian year in days?
Answer:
T = \(\frac{4 \pi^{2}}{\mathrm{GM}_{m}} \mathrm{R}^{3}\) M = \(\frac{4 \pi^{2}}{\mathrm{G}} \frac{\mathrm{R}^{3}}{\mathrm{T}^{2}}\)
Mm = \(=\frac{4 \times(3.14)^{2} \times(9.4)^{3} \times 10^{18}}{6.67 \times 10^{-11} \times(459 \times 60)^{2}}\)
Mm = 6.48 × 10 kg
Using Kepler’s III law,
\(\frac{\mathrm{T}_{\mathrm{M}}^{2}}{\mathrm{T}_{\mathrm{E}}^{2}}=\frac{\mathrm{R}_{\mathrm{MS}}^{3}}{\mathrm{R}_{\mathrm{ES}}^{3}}\)
Where RMS → Mars sun distance
RES → Earth – sun distance
∴TM = \((1.52)^{\frac{3}{2}}\) × 365
TM = 684 days.
Question 36.
‘Thermacole’ icebox is a cheap and efficient method for storing small quantities of cooked food in summer in particular. A cubical icebox of side 30 cm has a thickness of 5.0 cm. If 4.0 kg of ice is put in the box, estimate the amount of ice remaining after 6h. The outside temperature is 45° C, and co-efficient of thermal conductivity of thermacole is 0.01 J s-1m-1K-1. [ Heat of fusion of water = 335 × 10 J kg].
Answer:
Given, L = 3.36 × 105 Jkg-1 K = 0.01 Wm-1K-1
d = 0.05 m, t = 6 × 3600 = 21600s
A = 0.3 × 0.3 = 0.09 m2, θ1 ≈ θ2,= 45°C
We know that Q = \(\frac{\mathrm{KA}\left(\theta_{1}-\theta_{2}\right) \mathrm{t}}{\mathrm{d}}\) = mL
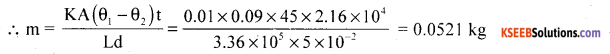
![]()
Question 37.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body?
Answer:
Spring constant = \(\frac{50 \mathrm{kg}}{0.2 \mathrm{m}}\) =250 kgm-1
We know that T = \(=2 \pi \sqrt{\frac{m}{k}}\) ; T = 0.6s (given)
i.e., m = \(\frac{\mathrm{kT}^{2}}{4 \pi^{2}}=\frac{250 \times(0.6)^{2}}{4 \times(3.142)^{2}}\)
m = 2.279 kg.