1st PUC Maths Model Question Paper 4 with Answers

Students can Download 1st PUC Maths Model Question Paper 4 with Answers, Karnataka 1st PUC Maths Model Question Paper with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 1st PUC Maths Model Question Paper 4 with Answers

Time: 3 Hrs 15 Min
Max. Marks: 100

Instructions:

1. The question paper has five parts namely A, B, C, D and E. Answer all the parts.
2. Part-A carries 10 marks. Part-B carries 20 marks. Part-C carries 30 marks. Part-D carries 20 marks, Part-E carries 10 marks.

Part – A

Answer ALL the questions. Each question carries one mark. (10 × 1 = 10)

Question 1.
Define power set of a set.
Answer:
All possible subset of a given set are called powerset.

Question 2.
If G = {7,8}, H = {5,4,2}, Find H × G.
Answer:
H × G = {(5.7),(5.8),(4,7),(4,8),(2,7),(2,8)}

Question 3,
Convert 225° into radian measure
Answer:

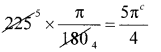
Question 4.
Express (2 – i) – (6 + 3i) in a + ib form.
Answer:
(2 – i) – (6 + 3i) = -4 -4i in the form (a + ib)

Question 5.
Find n, if nc₉ = ⁿc₈
Answer:
n = 9 + 8 = 17

Question 6.
Find 17th term of sequence whos: nth term is given by a = 4n – 3. term of sequence whos
Answer:
a₁₇ = 4(17) – 3 = 68 – 3 = 65

Question 7.
Define the slope of a straight line
Answer:
Slope = m = gradient or inclination of a line with respect to positive x-axis i.e., m = tan θ

Question 8.
Evalaute \(\lim _{x \rightarrow 0} \frac{(x+1)^{2}-1}{x}\)
Answer:

Question 9.
Write the negation of ” √2 is not a complex number.”
Answer:
~(√2 is not a complex no.) = √2 is a complex no.”

Question 10.
Two coins are tossed. Find a sample space.
Answer:
Sample space ={HH, HT,TT,TH}

Part – B

Answer any TEN Questions. (10 × 2 = 20 )

Question 11.
Let A = {1,2,3,4,5,6} and B = {2,4,6,8}, Find A – B and B – A.
Answer:
A – B = {1,3,5), (B – A) = {8}

Question 12.
If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements, Y has 32 elements, how many elements does X ∩ Y have?
Answer:
n(x ∪ y) = n(x) + (n ∪ y) – n(x ∩ y)
50 = 28 + 32 (x ∩ y) ⇒ [∴ n(X ∩ Y) = 10]

Question 13.
A function f is defined by f(x) = 2x – 5 write the value of (i) f(7) (ii) f(-3)
Answer:
Given f(x) = 2x – 5
∴ (i) f(7) = 2(7) – 5 = 9. (ii) f(-3) = 2(-3) – 5 = -11.

Question 14.
Find the angle in radian through which a pendulum swings, if its length is 75 cm and the tip describes an arc of length 10 cm.
Answer:
θ = ? r = 75 cm, s = 10 cm
S = rθ, (formula) 10 = 75 x θ.
∴ θ = \(\frac{10}{75}=\frac{2}{15}\) ⇒ ∴ θ = [0.133 radian.]

Question 15.
Find the solution of sin x = \(-\frac{\sqrt{3}}{2}\)
Answer:
α = \(-\frac{\pi}{3}\) ∴ G.S. x = 2nπ ± α
∴ [x = -2nπ ± \(-\frac{\pi}{3}\)]

Question 16
Write the Multplicative inverse of 4 – 3i.
Answer:

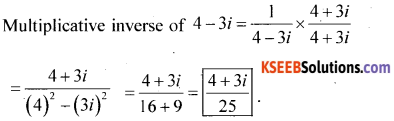
Question 17.
Solve the inequality 3(1 – x) <2 (x + 4) and represent the solution graphically on the number line.
Answer:
Given 3(1 – x) <2 (x + 4)
3 – 3x < 2x + 8 = 3 – 8 < 2x + 3x
-5 < 5x or 5x > -5 i.e., [x > -1]

Question 18.
Find the equation of straight line passing through the point (-4, 3) and having slope \(\frac { 1 }{ 2 }\)
Answer:
Equation of a straight line is givenby the formula
y – y₁ = m(x – x₁)
y = 3 = \(\frac { 1 }{ 2 }\)(x + 4) = 2y – 6 = x + 4 ⇒ ∴ [x – 2y + 10 = 0]

Question 19.
Find the distance between parallel lines 15x + 8y – 34 = 0, 15x + 8y + 31 = 0
Answer:

Question 20.
Find the equation of set of the points P such that ies distances from the points A(3, -4, 5) and B(-2, 1, 4) are equal.
Answer:
Given PA= PB where P =(x, y ,z)
∴ flash distance formula
\(\sqrt{(x-3)^{2}+(y-4)^{2}+(2+5)^{2}}=\sqrt{(x+2)^{2}+(y+1)^{2}+(z-4)^{2}}\)
(squaring on both sides)
∴ (x – 3)² + (y –  4)² + (2 + 5)² = (x + 2)² + (y – 1)² + (z – 4)²

∴(-6x – 4x) + (-8y + 2y) + (102 + 82) + (50 + 21) = 0 = 10x – 6y + 182 + 71 = 0 or
[10x + 6y – 182 – 71 = 0] equation of the plane.

Question 21.
Evaluate: \(\lim _{x \rightarrow 0}\left[\frac{1-\cos x}{x}\right]\)
Answer:

Question 22.
Write converse and contrapositive of “something is cold implies that it has low temperature”
Answer:
Converse: q → p = “Something has low temperature implies it is cold”.
Contrapositive: = q → -p= something does not have low temperature implies it is not cold.

Question 23.
Coefficient of ‘variation of distribution arc 60 and the standard deviat,on is 21. What is the arithmetic mean of the distribution?
Answer:
Given variation = 60
σ = 21, X̄ = ?
Take coefficient of variation = \(\frac{\sigma}{\bar{X}} \times \omega_{0}\)

X̄ = Arithmatic mean = 35.

Question 24.
A card is selected from a pack of 52 cards. Calculate the probability that the card is (i) an arc (ii) black card.
Answer:

Part – C

Answer any TEN of the following questions. Each question carries THREE marks. (10 × 3 = 30)

Question 25.
In a group of 65 people, 40 like cricket, 10 like cricket and tennis. How many like tennis only and not cricket? How many like tennis?
Answer:
n(C) = 40, n(T) = ? n( C ∩ T) = 10
n(C ∪ T) = ? n(T – C) = n(C ∪ T) = n(C) + A(T) – n(C ∩ T)
40 = 40 + n(T) -10 – 40 – 30 = n(T)
∴ [N(T) = 10] ⇒ n(T – C) = n(T)n(C ∩ T) = 10 – 10 = 0

Question 26.
Let A = {1,2,3,…14). Define a relation R from A to A by R = {{(x,y)}}: 3x – 4 = 0, x,y ∈ A}. Write its domain, co-domain and Range.
Answer:
R={(x,y): x ∈ A, y ∈ B, 3x – y = 0}
3(1) – 3 = 0, 3(2) – 6 = 0, 3(3) – 9 = 0, 3(4) – 12 = 0
∴ R = {(1,3), (2,6),(3,9),(4,12)}
Domain of R = A ⇒ Co-domain of R = A
Range of R = {3,6,9,12}

Question 27.
Prove that cos3x = 4cos³x – 3cosx.
Answer:
Take cos(A+B) =cos Acos B – sin Asin B
Put A = x, B = 2x
∴ cos(x + 2x) = cos x.cos2x – sin x sin 2x
cos(3x) = cos x(2cos²x – 1) – sin x(2 sin cos x)
= 2cos³x – cosx – 2cosx(sin²x) = 2cos³x – cosx – 2cosx(1 – cos²x).
= 2 cos³x – cos x – 2 cos x + 2cos³x [4cos³r – 3 cosx.]

Question 28.
Convert the complex number -1 -i into polar form.
Answer:
-1 -i = r(cosθ + isinθ) polar form

∴ r = \(\sqrt{x^{2}+y^{2}}=\sqrt{1+1}=\sqrt{2}\)
θ = tan^-1y/x = tan^-1\(\left(\frac{-1}{-1}\right)\) = -(π – standard) = \(-\left(\pi-\frac{\pi}{4}\right)=-\frac{3 \pi}{4}\)

Question 29.
If x + iy = \(\frac{a+i b}{a-i b}\) prove that x² + y²
Answer:

Question 30.
How many words with or with out meaning can be made from the letters of the word “Monday” assuming that no letters is repeated if
(i) 4 letters are used at a time.
(ii) All letters are used at a time.
(iii) All letters are used but first letter is a vowel.
Answer:
Monday : Given number of letters = 6
∴ total number of permutation = 6P₆ = 6!= 720
(i) It 4 letters are together = 3! × 4!= 6 × 24 = 144
(ii) All letters are used at a time. = 6! = 720
(iii) All letters are used but 1st letter is a vowel = 5!= 120 .

Question 31.
Find the middle term in the expansion of \(\left(3-\frac{x^{3}}{6}\right)^{7}\)
Answer:
x = 3, a = \(-\frac{x^{3}}{6}\), n = 7, T_n = ? r = 3
T_n = ? r = 4
n = 7 (add) no. there are two middle terms.

Question 32.
Insert Five numbers between 8 and 26 such that the resulting sequence is an arithmetic progression.
Answer:
Let the five AM’s are A₁, A₂, A₃, A₄, A₅ ∴ 5 AM’s are
∴ 8, A₁, A₂, A₂₃, A₄, A₅, A₆ ∴ A₁ = 11
n = 7, a = 8, d = ?, a_n = 26. A₂ = 14
an = a + (n – 1) d. A₃ = 17.
2b = 8 + (7-1)d A₄ = 20
∴ [d = 3] A₅ = 23

Question 33.
Find sum t0 n terms of sequence 8, 88, 888, 88888,..
Answer:
Let S_n = 8 + 88 + …… + n terms
S_n = 8{1 + 11 +……… + n terms}
X^ly by 9 on both side
∴ \(\frac{95 n}{8}\) = 9 + 99 + 999 +…. + to n term
GP

Question 34.
Find the coordinates of focus, directrix and latus rectum of parabola y² = 8x.
Answer:
Equation of parabola y² = 8x compare with the standard form
y² = 4ax ∴ 4a = 8 ∴ a = 2
∴ focus = (a,0) = (2,0)
Equation of directrix : x = -a.
x = -2 or [x + 2 = 0]
Latus rectum = 4a = 8.

Question 35.
Find the derivative of sin x with respect to x from 1st principle.
Answer:
y = sin x as x → x + Δx, y + Δy
∴ (y + Δy) = sin(x + Δx)
Δy = sin(x + Δx) – y
Δy = sin(x + Δx) – sin x
÷ Δx and apply lt Δx → 0 on both side

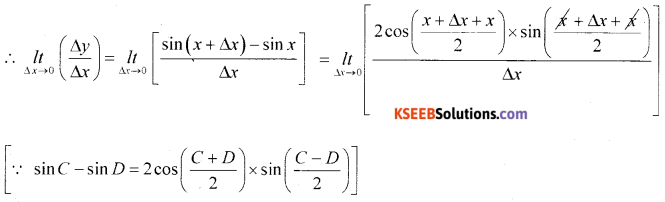
Question 36.
Using method of contradiction verify “√2 is irrational.”
Answer:
Let us assume that √2 is rational i.e.. the gives statement is false.
∴ √2 = \(\frac { 1 }{ 2 }\) ≠ 0 a and b have no conunon factor.
Squaring ∴ 2 = \(\frac{a^{2}}{b^{2}}\) ⇒ [a² = 2b²] ⇒ 2 divides a
Again put a = 2C(C ∈ Z) ⇒ ∴ (2c)² = 2b²
∴ 4c² = 2b² or [b² = 2c²] 2 divide b
i.e., 2 divides both a and b hence our assumption is i.e.. a and b does flot have common contradict out statement √2 is rational is false.
∴ √2 is irrational.

Question 37.
If A and B are events such that P(A) = 0.42, P(B)=0.48, P(A and B) = 0.16 determine
(i) P (not A)
(ii) P (not B)
(iii) P (A or B).
Answer:
P(A) = 0.42 P(8) = 0.48, P(A ∩B) = 0.16
(i) P( A¹ = 1 – 0.42 = 0.58 (ii) P(B¹) = 1 – 0.48 = 0.52
(iii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0.42 + 0.48 – 0.16 = 0.50 – 0.16 = 0.74.

Question 38.
A committee of two persons is selected from two men and two women. What is the probability that the committee will have
(i) no man ?
(ii) one man?
(iii) two men?
Answer:

(i) Probability (no man) = women × men = 2C₂, × 2C₀ = 1
(ii) Probability (one man) = 2C₁ × 2C₁ = 2 × 2 = 4
(iii) Probability (two even) = 2C₀ × 2C₂ = 1

Part – D

Answer any SIX Questions. (6 × 5 = 30)

Question 39.
Define signum function. Draw the graph. Also write its Domain and Range.

Question 40.
Prove that \(\frac{\sin 5 x-2 \sin 3 x+\sin x}{\cos 5 x-\cos x}=\tan x\)
Answer:

Question 41.
Prove by Mathematical induction that for all n ≥ 1
1² + 2² + 3² +…+ n² = \(\frac{n(n+1)(2 n+1)}{6}\)
Answer:

Question 42.
Solve the system of inequalities graphically x + 2y ≤ 10, x + y ≥1, x – y ≤ 0, x ≥ 0, y ≥ 0.
Answer:

Question 43.
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected, if the team has (i) no girls (ii) atleast one boy and one girl? (iii) atleast 3 girls
Ans.
Given 4 girls, 7 boys
Select 5 members

(ii) atleast 1 B and 1 G
(a) 4C₁ × 7C₄ = 140
(b) 4C₂ × 7C₃ = 210
(e) 4C₃ × 7C₂ = 21
(d) 4C₂ × 7C₁ = 7
Total number of selection: 378ways.

Question 44.
State and prove Binomial theorem for positive integer n.
Answer:

Question 45.
Derive the equation of straight line in the form xcosω + ysin ω = P, where P is length of normal to the line from origin, w is the inclination of normal with positive x-axis.
Answer:
Carried a line cutting X-axsis at A and Y axis at B.
Let OA = a, OB = b are x and y interscept.
∴ By intercept form of equation of line.
\(\frac{x}{a}+\frac{y}{b}=1\) is the equation of the line AB.
Draw OM ⊥ AB. i.e., normal line
Let OM = P. ∴ In O OAM
cosω = \(=\frac{O M}{O A}=\frac{P}{\cos w}\)  ⇒ ∴ a = \(\frac{O M}{O B}=\frac{P}{b}\)

Question 46.
Derive an expression for the co-ordinates of a point that divides the line joining points A(x¹, y¹, z¹) and B(x², y², z²) internally in the ratio m : n. Hence find the coordinates of the mid point of AB where A = (1,2,3) and B = (5,6,7).
Answer:
Proof: Let p(x₁, y₁, z₁) and Q(x₂, y₂, z₂) be the given points
Let R(x, y, z) divide PQ internally in the ratio m : n
Draw PL, QM, RN perpendicular to xy-plane.
∴ PL ∥ RN ∥ QM
∴ PL, RN, QM lie in one plane
So that the points L, N, M lie in a straight line which is the intersection of the plane and XY plane.
Through the point R draw a line AB It to the line LM. The line AB intersect the line LP externally at A and the line MQ at B.

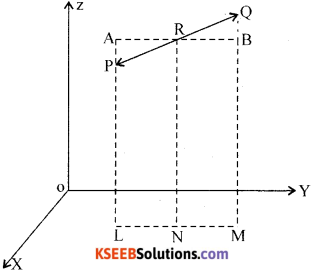
Triangle APR and LIQR are similar.

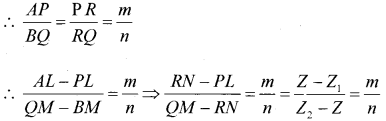
∴ n(z – z₁) = m(z₂ – z)
∴ nz = nz₁ = mz₂ – m₂
∴ (nz + mz) = (mz₂ + nz₁)
∴ z(m + n) = mz₂ + nz₁

Question 47.
Prove that \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\), where x measured in radians. Also evaluate \(\lim _{x \rightarrow 0}\left(\frac{\sin 4 x}{x}\right)\)

Question 48.
Find mean deviation about mean for the data.

Answer:

Part – E

Answer any ONE question. (1 × 10 = 10)

Question 49.
(a) Prove geometrically that cos(x + y) = cos x cos y – sin xsin y. and hence deduce that cos 2x cos²x – sin²x.
Answer:
Prove that cos(x + y) = cos x cos y.sin x sin y

Proof Consider a unit circle (radius = 1 unit) with centre is (0, 0).
Consider 4 point P₁, P₂, P₃ and P₄

The co-ordinate of P₁, P₂, P₃ and P₄ are given by
P₁ = (cosx,sinx) P₂ = [cos(x + y). sìn(x + y)]
P₃ = [cos(-y) sin(-y)] P₄ = [1,0]
From the figure OP₁OP₃ is congruent to ∆P₂OP₄
∴ From distance formula
P₁p₃ = P₂P₄ …… (1)
Takè the distance (P₁P₃)² = [cosx – cos(-y)]² + [sin x – sin (-y)]²
= (cosx – cosy)² + (sin x + sin y)²
= cos²x + cos²y = cosxcosy + sin²x + sin²y + 2sin cosy = 1 + 1 + 2(cosxcosy – sinxsiny)
(p₁, P₃)² = 2 – 2 cos (x + y)
Again (P₂P₄)² = [1^{(a-b)2-cos(x+y)}]² + |q – sin (x + y)|²
= 1 + cos²(x + y) -2cos(x + y) + sin²(x + y) = 1 + 1 – 2cos(x + y) = 2 – 2cos(x + y)

⇒ LHS = RHS
∴ [cos(x + y) = cosx cosy – sin x sin y]

(ii) Show that cos 2x = cos²x – sin x²x
Take cos(x + y) = cos xcos y – sin xsin y
Put y = x
∴ cos(x + x) = cosx cosx – sinx sinx
cos2x = cos² x – sin²x

(b) Find the sum to n terms of the series 1 × 2 + 2 × 3 + 3 × 4 +…
Answer:
(1 × 2) + (2 × 3) + (3 × 4) +……+ n term nth term.

n^2th term, 9n = n(n + 1), an = n² + n
to find the sum apply Σ on both side
∴ Σan = Σn² + n

Question 50.
(a) Define hyperbola as a set of points. Derive its equation in the standard form \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Answer:
Definition: “Hyperbola is the set of all points in a plane the difference of where distances from the fixed point in the plane is constant.”
Derivain: prove that \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) (standard hyperbola equation)
Let F₁, and F₂, are the two fixed point called focii of the hyperbola. The unit point of the sine segment. Joining the Foci is called the centre of the hyperbola.

A line through the Foci is called the transverse axis. And the line through the centre of perpendicular to the transverse axis is called conjugate axis.
Assume the distances between the two focii is “2c’ the distance between two and define the quantity ‘b’ as b = \(\sqrt{c^{2}-a^{2}}\) and 2b is the length of the conjugaton, (PF₂ – PF₁ = 2a = transverse axis)

The coordinate of F₁ = (-0,0) and F₂, =(0,0)
Let P(x,y) be a junction the hyperbola such that the distance of the distance from P to the farter point be “2a’ i.e., PF₁ – PF₂ = 2a ∴ from the distance formula


Again squaring on both side. \(\therefore\left(\frac{x c}{a}-a\right)^{2}=(x-c)^{2}+y^{2}\)
On simplification further to get \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{c^{2}-a^{2}}=1\)
put c² – a² = b²
∴ the standard form of hyperbola equation is
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)

(b) Find the derivative of \(\frac{x^{5}-\cos x}{\sin x}\) with respect to x
Answer: