Students can Download 1st PUC Maths Model Question Paper 1 with Answers, Karnataka 1st PUC Maths Model Question Paper with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Maths Model Question Paper 1 with Answers
Time : 3 hrs 15 min
Max. Marks : 100
Instructions:
1. The question paper has five parts A, B, C, D and E and answer all parts,
2. Part-A carries 10 marks, Part-B carries 20 marks, Part-C carries 30 marks, Part-D carries 20 marks, Part-E carries 10 marks.
Part – A
Answer any TEN questions : (10 × 1 = 10)
Question 1.
Given that the numbers of subsets of a set A is 16. Find the number of elements of A.
Answer:
Let n(A) = m
n [P(A)] = 16 ⇒ 2m = 16 ⇒ m= 4
n(A)= 4
Question 2.
If tan x = \(\frac { 3 }{ 4 }\) and x lies in the third quadrant, find sin X.
Answer:
tan x = \(\frac{3}{4}=\frac{-3}{-4}\)
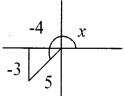
ordinate = -3, abscissa = 4, distance = 5 sin x = \(\frac { -3 }{ 5 }\)
Question 3.
Find the modulus of \(\frac{1+i}{1-i}\)
Answer:
\(\frac{1+i}{1-i}=\frac{(1+i)^{2}}{1-i}=\frac{2 i}{2}\) = i Modulus of i= 1
![]()
Question 4.
Find ‘n’ if nC7 = nC6
Answer:
nCn-7 = nC6 ⇒ n – 7 = 6 ⇒ n = 13.
Question 5.
Find 20th term of GP. \(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}—-\)
Answer:

Question 6.
Find the distance between 3r + 4y +5= 0 and 6x + 8y +2=0.
Answer:
3x + 4y + 5 = 0) ………….. (1)
3x + 4y + 1 = 0 …………. (2)
Required distance \(\left|\frac{5-1}{\sqrt{9+16}}\right|=\frac{4}{5}\) units
Question 7.
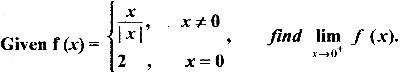
Answer:
\(\lim _{x \rightarrow 0+}\) f(x) = \(\lim _{x \rightarrow 0} \frac{x}{x}=\frac{1}{1}=2\) ∴ f(x) in Discontinuous
Question 8.
Write the negation of For all a, b ∈ I, a – b ∈ I’.
Answer:
“There exists a, b ∈ I, such that a – b € I’
or ‘∃ a, b ∈ I, a – b ∉ I’.
Question 9.
A letter is chosen at random from the word “ASSASINATION”. Find the probability that letter is vowel.
Answer:
No of ways of selecting one vowel out of six vowels (3A’S, 21’s, 10’s) = 6C1 = 6.
P(1 vowel) = \(\frac{^{6} \mathrm{C}_{1}}{^{13} \mathrm{C}_{1}}=\frac{6}{13}\)
Question 10.
Let A = {2,3,4} and R be a relation on A defined by
R={(x,y)|x,y ∈ A,x divides y}, find ‘R’.
Answer:
R= {(2, 2), (2, 4), (3, 3), (4,4)}.
![]()
Part – B
Answer any TEN questions : (10 × 2 = 20)
Question 11.
If A and B are two disjoimt sets and n(A) = 15 and n(B) = 10 find n(A ∪ B), n(A ∩ B)
Answer:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
n(A ∩ B) = 0, n(A ∪ B) = 15 + 10 = 25.
Question 12.
If U = {x:r s≤10, r ∈ N} A = {x : x ∈ N, x is prime) B = {x : x ∈ N, x is even} write A ∩ B’ in roster form.
Answer:
U = {1, 2, 3 … 10), A = {2, 3, 5, 7}
B = {2, 4, 6, 8, 10} B1 = {3, 5, 7,9}
[A ∩ B1 = {3,5,7)]
Question 13.
If A × B = {(a,1) (a,2) (a,3) (b,1) (b,2) (b,3)}, find the sets A and B and hence fimnnd B × A
Answer:
A = {a, b}, B = {1, 2, 3}
B × A= {(1, a) (1, b) (2, a) (2, b) (3, a) (3, b)}
Question 14.
The difference between two acute angles of a right angled triangle is to \(\frac{3 \pi}{10}\) radiAnswer: Express the angles in degrees.
Answer:
Let A and B be acute angles
Given A + B = \(\frac{\pi}{2}\) = 90° : A – B = \(\frac{3 \pi}{10}\) = 54° ⇒ A = \(\frac{2 \pi}{5}\) and B = \(\frac{\pi}{5} \) ⇒ A = 72 and B = 18°.
Question 15.
Find sin \(\frac{x}{2}\) if tan x = \(-\frac{4}{3}\)and x lies in second quadrant,
Answer:
tan x = \(\frac{-4}{3}=\frac{4}{-3}\) ⇒ ∴ cos x = \(\frac{-3}{5}\)
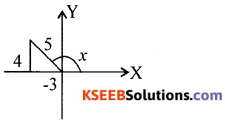
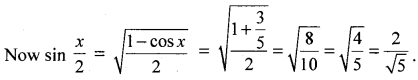
Question 16.
\(\lim _{x \rightarrow 3} \frac{x-3}{x^{2}-5 x+6}\)
Answer:
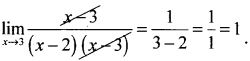
![]()
Question 17.
CV = 60 σ = 21
Answer:

Question 18.
Write the inverse, converse of ‘If a parallelogram is a square, then it is rhombus’.
Answer:
Inverse: If a parallelogram is not a square then it is not a rhombus
Converse: If a parallelogram is a rhombus then it is a square.
Question 19.
On her vacations Veena visits four cities A, B, C and D in random order. What is the probability that she visits A before B?
Answer:
n (S) = 24
P(visiting A before B) = \(\frac{12}{24}\) = 1/2
Question 20.
In a triangle ABC with vertex A(2,3), B(4, -1) and C(1,2). Find the Length of the alitude from vertex A.
Answer:
Equation BC = x + y – 3 = 0
Length of the alitude from A (2, 3) = \(\left|\frac{2+3-3}{\sqrt{2}}\right|=\left|\frac{2}{\sqrt{2}}\right|=\sqrt{2}\) = √2.
Question 21.
Represent the complex number z = 1 + i in polar form.
Answer:
r = √2 and θ = \(\frac{\pi}{4}\) Polar form is √2 \(\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)\)
Question 22.
Obtain all pairs of consecutive odd natural numbers such that in each pair both are more than 50 and their sum is less than 120.
Answer:
Taking the pair as x, x + 2,
we get x > 50, 2x + 2 < 120 ⇒ x < 59 and writing the required pairs are (51, 53), (53, 55), (55, 57), (57, 59).
![]()
Question 23.
A line cuts off equal intercepts on the co – ordinate axes. Find the angle made by the line with the positive x-axis.
Answer:
Slope =-1 ⇒ tanθ = -1
angle made = 135°.
Question 24.
If the origin is the centroid of the triangle PQR with vertices P (2a, 4, 6) Q(-4, 3b, -10) and R(8, 14, 2c) then find the values of a, b, c.
Answer:

Part-C
Answer any EIGHT of the following questions : (10 × 3 = 30)
Question 25.
Out of a group of 200 students (who know at least one language), 100 students know English, 80 students know Kannada, 70 students know Hindi. If 40 students know all the three languages, find the number of students who know exactly two languages.
Answer:
writing n(E)= 100, n(K)= 80, n(H)= 70 .
n(E ∪ K ∪ H) = 200, n (E ∩ K N ∩ H) = 40
We know that n(E ∪ K ∪ H) = n(E) + n (K) + n(H) –n (E ∩ K)
– n (K ∩ H) -n (H ∩ E) + n (E ∩ K ∩ H)
∴ n (E ∩ K) + n (K ∩ H) + n (H ∩ E) = 90
Question 26.
Let R: Z → Z be a relation defined by R = {(a,b) : a, b, ∈ Z, a – b ∈ z}. Show that
(i) ∀ a ∈ Z, (a, a) ∈ R.
(ii) (a, b) ∈ R ⇒ (b,a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R
Answer:
∀ a ∈ Z, (a, a) ∈ R since a – a = 0 ∈ Z
(a, b) ∈ R ⇒ a – b ∈ Z ⇒ ∴ b – a ∈ Z ⇒ (b, a) ∈ R
(a, b) ∈ R, (b, c) ∈ R ⇒ a – b ∈ Z, b – C ∈ Z
∴ a – b + b – c ∈ Z ⇒ (a, c) ∈ Z
![]()
Question 27.
Prove that (cos x + cos y)2 + (sin x – sin y)= 4cos2 \(\left(\frac{x+y}{2}\right)\)
Answer:
LHS = cos2x + cos2 y + 2 cos x cos y + sin2x + sin2y – 2sin x sin y
= 1 + 1 + 2 (cos x cos y – sin x sin y) = 2 [1 + cos (x + y)] = 4cos2 \(\left(\frac{x+y}{2}\right)\)
Question 28.
Solve: √2x2 + x + √2 = 0.
Answer:
√2x2 + x + √2 = 0; Here a = √2, b = 1,c = √2
∴ D = 52 – 4ac = (1)2 – 4(√2)(√2) = 1 – 8 = -7
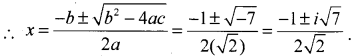
Question 29.
How many letters words with or with out meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if.
(i) 4 letters are used at a time,
(ü) all letters are used at a time
(iii) all letters are used but first letter is a vowel?
Answer:
There are 6 letters in the word MONDAY. So, the total number of words is equal to the number of arrangements of these letters taken four at a time.
The number of such arrangements = 6P4 = \(\frac{6 !}{(6-4) !}=\frac{6 !}{2 !}=\frac{6.5 .4 .3 .2 .1}{2.1}\) = 360
Hence, total number of words = 360
(ii) Total number of arrangements in this case = 6P6 = 6! = 720
(ii) Total number of arrangements when all letters are used but the first letter is a vowel
= 2 × 5P5 = 2 × 5! = 2 × 5 × 4 × 3 × 2 × 1 = 240.
Question 30.
If x + iy = \(\frac{2+i}{2-i}\) then prove that x2 + y2
Answer:
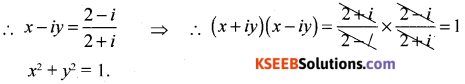
Question 31.
Find the term independent of x in the expansion of \(\left(\frac{3}{2} x^{2}-\frac{1}{3 x}\right)^{6}\)
Answer:
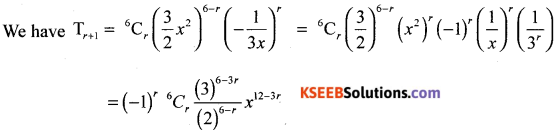
The term will be independent of x if the index of x is zero, i.e., 12 – 3r= 0. Thus, r=4
Hence 5th term is independent of x and is given by (-1)4 6C4 \(\frac{(3)^{6-8}}{(2)^{6-4}}=\frac{5}{12}\)
![]()
Question 32.
8, A1, A2, A3, 24
Answer:
Tn = a + (n − 1)d
24 = 8 + (5 – 1)d
16 = 4d ⇒ d = 4
3 Am’s are 12, 16, 20.
Question 33.
(i) At least one man.
Answer:
1 man and I woman
or 2
men and 0 women
= 2C1 × 2C1 + 2C2 × 2C0 = 2 × 2 + 1 × 1 = 4 + 1 = 5.
(ii) At most one man
Answer:
1 men and 1 women
or
0 men and 2 women
= 2C1 × 2C1 + 2C0 × 2C2 = 2 × 2 + 1 × 1 = 4 + 1 = 5.
Question 34.
Find the derivative of the function ‘cos x’ w.r.t ‘x’ from first principle
Answer:
Let f ‘(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
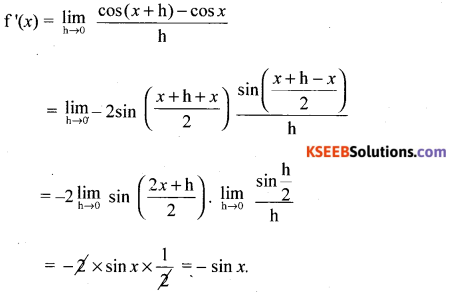
Question 35.
A parabola with vertex at origin has its focus at the centre of x2 + y2 – 10x + 9 = 0 Find the direction its directrix and latus rectum.
Answer:
The centre of the circle = (5,0).
The equation y2 = 20x ⇒ y2 = 4ax ⇒ a = 5
directrix is x = -5, LR = 20.
Question 36.
If an A.P. if mth term is n and the nth term is m, where m ≠ n, find the pth term
Answer:
We have
am = a + (m – 1) d = n, …… (1)
and an = a + (n – 1) d = m …….. (2)
Solving (1) and (2), we get
(m, n) d = n – m, or d = -1,
and a = n + m – 1 ……. (3)
Therefore ap = a + (p – 1)d ……. (4)
= n + m – 1 + (p – 1) (-1)= n + m – p
Hence, the pth term is n + m – p.
![]()
Question 37.
Verify by the method of contradiction that √2 is irrational
Answer:
If possible Let √2 is rational
∴ √2 = \(\frac{p}{q}\), p, q ∈ z, q ≠ 0
We assume that p and q donot have any common factor
p = √2q ⇒ p = 2q2
p2 is a multiple of 2 ⇒ ∴ p is a multiple of 2
∴ p = 2k, k ∈ z ⇒ p2 = 4k
2q2 = 4k2 ⇒ q2 = 2k2
q2 = 2k2
q2 is a multiple of 2 ⇒ ∴ q is a multiple of z
∴ p and q are both multiple of 2 and hence has a common factor z which is a contradiction
∴ our assumption is wron
∴ √2 is irrational
Question 38.
Two students Anil and Sunil a appear in the examination The prpbability that Anil will qualify in the examination is 0.05 and that Sunil will qualify is 0.10. The probability that both will qualify in the examination is 0.02. Find the probability that Anil and Sunil will not qualify in the examination.
Answer:
Let A, B denote the events that Anil, Sunil qualify in the exam
P (A) = 0.05, P(B) = 0.1, P (A ∩ B) = 0.02
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0.05 + 0.1 – 0.02 = 0.13
P(A’ ∩ B’) = 1 – P (A ∪ B) = 1 – 0.13 = 0.87.
Part – D
Answer any Six questions : (6 × 5 = 30)
Question 39.
Define signum function. Draw the graph of the signum function. Also write its domain and range.
Answer:
Singum function :
The function f:R → R defined by
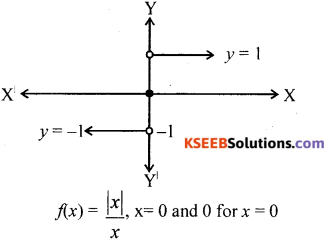
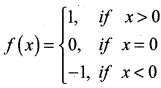
is called the signum function. The domain of the signum function is R and the range is the set {-1, 0, 1}.
![]()
Question 40.
Prove that \(\lim _{\theta \rightarrow 0} \frac{\sin \theta}{\theta}=1\) (q being in radians) and hence show that \(\lim _{\theta \rightarrow 0} \frac{\tan \theta}{\theta}=1\)
Answer:
Consider a circle with centre O and radius ‘r’ Mark two points A and B on the circle so that
![]()
Join AB. Draw BM ⊥ OA
From the figure it is clear that.
Area of ∆OAB < Area of sector OAB < sector of ∆OAC …. (1)
Area of ∆OAB = \(\frac { 1 }{ 2 }\) OA.BM
[In ∆OBM. Sin θ \(\frac{\mathrm{BM}}{r}\) ⇒ BM = r Sin θ ]
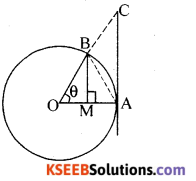
∴ Area of ∆OAB = \(\frac { 1 }{ 2 }\) r r. sin θ = \(\frac { 1 }{ 2 }\)r2 sin θ
Area of sector OAB = \(\frac { 1 }{ 2 }\) r2θ
Area of ∆OAC = \(\frac { 1 }{ 2 }\) OA.AC
= \(\frac { 1 }{ 2 }\)r2 tan θ [In ∆OAC, tan θ = \(\frac{A C}{O A}=\frac{A C}{r}\) ⇒ AC = r tan θ]
∴ (1) becomes
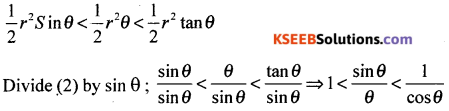

Question 41.
12 + 22 + 32 + ………… + n2 = \(\frac{n(n+1)(2 n+1)}{6}\)
Answer:
Let P(n) : 12 + 22 + 32 + ………… + n2 = \(\frac{n(n+1)(2 n+1)}{6}\)
step 1 : Prove that P(1) is true
when n= 1; L.H.S = 12 = 1
R.H.S = \(\frac{1(1+1)(2+1)}{6}\)
∴ L.H.S = R.H.S ⇒ ∴ P(1) is true
step 2: Assume that P(m) is true
i.e., 12 + 22 + 32 + ………… + m2 = \(\frac{m(m+1)(2 m+1)}{6}\) …… (i)
step 3: Prove that P(m + 1) is true
i.e., 12 + 22 + 32 + ………… + m2 + (m+1)2 = \(\frac{(m+1)(m+2)(2 m+3)}{6}\)
L.H.S = [12 + 22 + 32 + ………… + m2] + (m+1)2

= R.H.S ⇒ ∴ P(m+1) is true
Conclusion: P(1) is true ⇒ P(m) is true ⇒ P(m+1) is true
∴ By principle of mathematical induction, the result is true for all natural numbers ‘n’.
![]()
Question 42.
A group consists of 7 boys and 5 girls. Find the number of ways in which a team of 5 members can be selected so as to have atleast one boy and one girl.
Answer:
Number of ways of selecting
1 B and 4 G = 7C1 × 5C4 = 35
2 B and 3G = 7C2 × 5C3 = 210
3 B and 2 G = 7C3 × 5C2 = 350
4. B and 1 G = 7C4 ×5C1 = 175
Total number of selections = 770.
Question 43.
State and prove binomial theorem for positive integers.
Answer:
Statement: “If’n’ is a +ve integer then
(x + a)n = nC0 xn a0 + nC1 xn-1 a1 + nC2 xn-2 a2 + ………….. + nCn x0 an.
Proof : (By Mathematical induction):
Let p(n) : (x + a)n = nC0 xn a0 + nC1 xn-1 a1 + nC2 xn-2a2 + ………….. + nCn x0 an.
Step1 : Prove that P(1) is true
when n = 1, L.H.S = (x + a)1 = x + a; RHS = 1c0 x1 a0 + 1c1 x0 a1 = 1.x.1 + 1.1.a = x+a
L.H.S. = R.H.S. ⇒ ∴ P(1) is true
Step 2: Assume that P(m) is true
i.e., (x + a)m = mc0 xm a0 + mc1 xm-1 a1 + mc2 xm-2 a2 + ………….+ mcmx0am …….(i)
Step 3 : Prove that P(m + 1)m+1 is true
i.e. (x + a)m+1 = m+1c0 xm+1 a0 + m+1c1 xm a1 + m+1c2 xm-1 a2 + …….. + m+1cm+1 x0 am+1
Multiply both sides of equation (i) by (x+a)
∴ (x + a)m (x + a) = (x + a) [mc0 xm a0 + mc1 xm-1 a1 + mc2 xm-2 a2 + ………….+ mcmx0am]
(x + a)m+1 = x [mc0 xm a0 + mc1 xm-1 a1 + mc2 xm-2 a2 + ………….+ mcmx0am] + a [mc0 xm a0 + mc1 xm-1 a1 + mc2 xm-2 a2 + ………….+ mcmx0am]
(x + a)m + 1 = mc0xm+1 a0 + mc1xma1 + mc2 xm-1 a2 + ……. + mcm x0 am+1
= mc0xm+1a0 + (mc1 + mc0)xm a1 + (mc2 + mc1) xm-1 a2 + ………… + (mcm + mcm-1) x1 am + mcm x0 am+1
(x + a)m+1 = m+1c0 xm+1 a0 + m+1c1 xm a1 + m+1c2 xm-1 a2 + …….. + m+1cm+1 x0 am+1
[∴ mcm = m+1c0
mc1 + mc0 = m+1c1
mc2 + mc1 = m+1c2
m+1cm]
⇒ ∴ P(m + 1) is true
Conclusion: P(1) is true, P(m) is true ⇒ P(m+1) is true
∴ By principle of mathematical induction the result is true for all natural numbers n.
Notes: 1. The number of terms in the expansion of (x + a)n is n + 1.
2. The Gen term of binomial expansion is Tr+1 = ncr xn-r ar.
![]()
Question 44.
Derive an expression for the coordinates of a point that divides the line joining the points A(x1, y1, z1,) and B (x2, y2, z2.) internally in the ratio m : n. Hence, find the coordinates of the midpoint of AB where A = (1, 2, 3) and B = (5, 6, 7).
Answer:
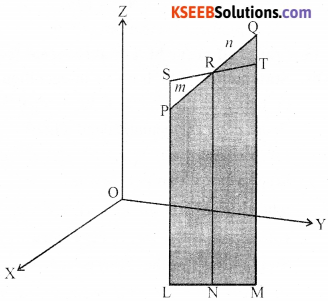
Let the two given points be P (x1, y1, z1,) and Q (x2, y2, z2). Let the point R (x, y, z) divide PQ in the given ratio m : n internally, Draw PL,
QM and RN perpendicular to the XY-plane. Obviously PL ∥ RN ∥ QM and feet of these perpendiculars lie in a XY-plane. The points L, Mand N will lie on a line which is the intersection of the plane containing PL, RN and QM with the XY-Plane. Through the point R draw a line ST parallel to the line LM. Line ST will intersect the line LP externally at the point S and the line MQ at T, as shown in Fig 12.5.
Also note that quadrilaterals LNRS and NMTR are parallelograms.
The triangles PSR and QTR are similar. Therefore,
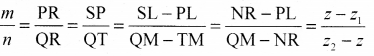
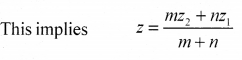
Similarly, by drawing perpendiculars to the XZ and YZ-planes, we get
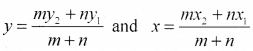
Hence, the coordinates of the point R which divides the line segment joining two points P(x1, y1, z1) and Q(x2, y2, z2,) internally in the ratio m: n are
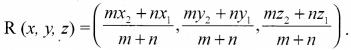
![]()
Question 45.
Derive a formula for the angle between two lines with slopes m1 and m2. Hence find the slopes of the lines which make an angle \(\frac{\pi}{4}\) with the line x – 2y + 5 = 0.
Answer:
m1 = tan θ1, m2 = tan θ2
Question 46.
Prove that \(\frac{\cos 4 x+\cos 2 x+\cos 3 x}{\sin 4 x+\sin 2 x+\sin 3 x}=\cot 3 x\)
Answer:

Question 47.
Solve graphically 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Answer:
2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6 …..(1)
Points A(2, 0) and B(0,4) lie on 2x + y = 4
Plot the points and join them to get line AB
(0,0) does not satisfy 2x + y ≥ 4
⇒ Half plane given by 2x + y ≥ 4 is away from origin …..(2)
Points C(3, 0) and D(0, 3) lie on x + y= 3
Plot the points and join them to get line CD.
(0,0) satisfies x + y ≤ 3 ….. (3)
⇒ Half plane given by x + y ≤ 3 is towards origin
Points C(3, 0) and E(0, -2) lie on 2x – 3y = 6
Plot the points and join them to get line CE.
(0,0) satisfies 2x – 3y ≤ 6
⇒ Half plane given by 2x – 3y ≤ 6 is towards origin
From (2), (3), (4) common region shown shaded in figure represents solution of (1).
![]()
Question 48.
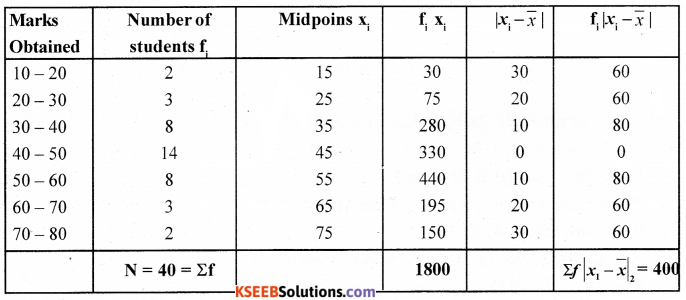
Find the mean deviation about the mean for the following data.

Answer:
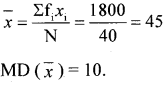
Part – E
Answer any ONE questions : (1 × 10 = 10)
Question 49.
(a) To cos (A + B) = cos x. cos y – sin x sin y and hence find cos 75°.
Answer:
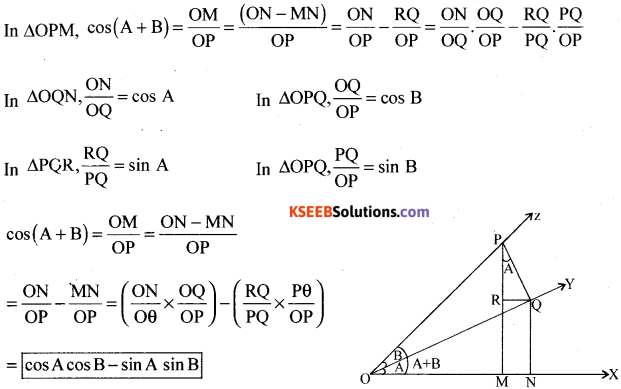
(i) becomes
∴ cos (A + B)= cos A.cos B – sin B
cos 75° = cos (45 +30)
= cos 45 cos 30 – sin 45 sin 30
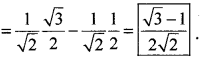
![]()
(b) Find the sum to n terms of the series 12 + (12 + 22) + (12 + 22 + 32) + ……..
Answer:
nth term Tn = 12 + (12 + 22) + (12 + 22 + 32) + ……. + n2 = \(\frac{n(n+1)(2 n+1)}{6}=\frac{2 n^{3}+3 n^{2}+n}{6}\)
∴ Tn = \(\frac{2 n^{3}+3 n^{2}+n}{6}\)
Sum to n terms, Sn = ΣTn
= \(\frac{1}{6}\) [2Σn3 +3Σn2 + Σn]
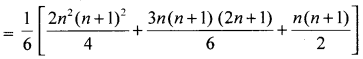
∴ Sn = \(\frac{n(n+1)^{2}(n+2)}{12}\)
Question 50.
(a) An elipse is the set of all ninte in a plane tha e of whose distance from two fived points in the need of all points in a plane the sun of whose distance points in the plane is a constant.
Answer:

Let F1 and F2 be the foci and O be the mid point of the line segment F1F2 Let O be the origin and the line from 0 through F2 be the positive x-axis and that through F1 as the negative x-axis. Let, the line through O perpendicular to the x-axis be the y-axis. Let the coordinates of F1 be (-c, 0) and F2 be (c, 0).
Let P(x, y) be any point on the ellipse such that the sum of the distances from P to the two foci be 2a
i.e., PF1 + PF2 = 2a. …(1)
Using the distance formula, we have
\(\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2 a\)
i.e., \(\sqrt{(x+c)^{2}+y^{2}}=2 a-\sqrt{(x-c)^{2}+y^{2}}\)
Squaring both sides, we get
(x + c)2 + y2 = 4a2 – 4a \(\sqrt{(x-c)^{2}+y^{2}}\) + (x – c)2 + y2
which on simplification gives
\(\sqrt{(x-c)^{2}+y^{2}}=a-\frac{c}{a} x\)
Squaring again and simplifying, we get

![]()
(b) \(y=\frac{x^{5}-\cos x}{\sin x}\)
Answer:
