Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2020 (South), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2020 (South)
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART-A
I. Answer any TEN questions. (10 × 1 = 10)
Question 1.
Write the imaginary part of the complex number \(\)
Answer:
Imaginary part = \(\).
Question 2.
If A = {a, b, c, d, e}, B = {a, b, e, f} find A ∩ B
Answer:
A∩B = { a, b, e]
Question 3.
Simplify \(\left(x^{\frac{1}{2}}+y^{\frac{1}{2}}\right)\left(x^{\frac{1}{2}}-y^{\frac{1}{2}}\right)\)
Answer:
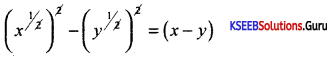
Question 4.
Form the quadratic equation whose roots are (2, -3).
Answer:
x2 – (2-3)x + (2-3) = 0
x2 + x – 6 = 0
![]()
Question 5.
Find the 8th term of the sequence \(\frac{1}{2}, \frac{1}{4}, \frac{1}{6}\) ………….
Answer:
a8 = \(\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)^{8-1}=\left(\frac{1}{2}\right)^{8}=\frac{1}{256}\)
Question 6.
Write log8 16 = 4/3
Answer:
![]()
Question 7.
Define annuity.
Answer:
A certain amount that is paid periodically is known as an annuity.
Question 8.
Find the simple interest on Rs. 500 at 5% for 5 years.
Answer:
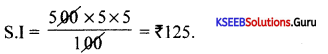
Question 9.
Express \(\frac{7 \pi}{6}\) radians into degrees.
Answer:
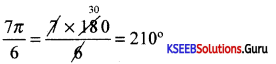
Question 10.
Convert 0.12 into a percentage.
Answer:
(0.12 × 100) = 12%
Question 11.
Find the slope of the line perpendicular to the line 3x – 4y + 5 = 0.
Answer:
Slope = m = \(\frac{-(3)}{4}=\frac{3}{4}\)
Question 12.
Find the value of sin60° + cos60°.
Answer:
= \(\frac{\sqrt{3}}{2}+\frac{1}{2}=\frac{\sqrt{3}+1}{2}\)
Part-B
II. Answer any TEN questions. (10 × 2 = 20)
Question 13.
Find the number of positive divisors of 360.
Answer:
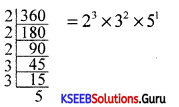
T(N) = (3+1)(2+1)(1+1) = 4 × 3 × 2 = 24
![]()
Question 14.
Find the HCF of 18 and 24.
Answer:
HCFof 18 and 24 = 6

Question 15.
If A = {a, b, c, d} and B = {d, e, f, g, h, i} find A – B and B – A.
Answer:
A – B = {a, b, c}
B – A = {e,f g, h, i}
Question 16.
Simplify \(\frac{2^{n+1}+2^{n-1}}{2^{n}+2^{n+2}}\)
Answer:

Question 17.
If K + 9, K – 6 and 4 are in GP. then find the value of k.
Answer:
Common ratio \(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}}=\frac{\mathrm{T}_{3}}{\mathrm{~T}_{2}}\)
\(\frac{K-6}{K+9}=\frac{4}{K-6}\)
∴ (K-6)2 = 4(K + 9)
![]()
K2 = 16K
∴ K = 16
Question 18.
If α & B are the roots of the equation x2 + 5x + 6 = 0 then find the value of \(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}\).
Answer:
α + β = -b/a = -5 αβ = c/a = 6
\(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}=\frac{\alpha^{2}+\beta^{2}}{\alpha \beta}=\frac{(-5)^{2}-2(6)}{6}=\frac{13}{6}\)
Question 19.
The sum of two consecutive numbers is 23. Find the numbers.
Answer:
Assume the two consecutive no. are x and x + 1
∴ x + (x + 1) = 23
∴ 2x = 2
∴ x = 1
the numbers are 11 and 12
![]()
Question 20.
Solve 2x + 6 < 0, x ∈ z the inequality in one variable and represent the solution on the number line.
Answer:
2x + b < 0
∴ x < -3
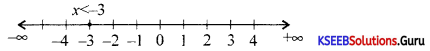
Question 21.
Find the future value of an annuity of ₹ 5000 at 12% p.a. for 6 years.
Answer:
A = Rs.5,000
r = 0.12
n = 6
F = \(\frac{A\left[(1+r)^{n}-1\right]}{r}=\frac{5000\left[(1+0.12)^{6}-1\right]}{0.12}=\frac{4869.11}{0.12}\) = 40,575.9
Question 22.
The weight of 6 men are 90 kg, 70.5kg, 56 kg, 45.5kg, 85 kg and 78 kg. Find the average.
Answer:
Average weight = \(\frac{90+70.5+56+45.5+85+78}{6}\) = 70.83
Question 23.
Prove that \(\sqrt{\frac{1+\cos x}{1-\cos x}}\) = cosec x + cot x.
Answer:
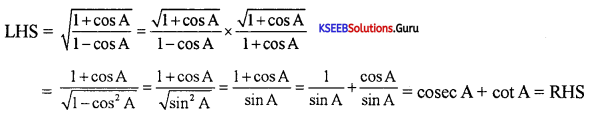
Question 24.
Evaluate sin2 π/6 + cos2 π/3 = tan2 π/4 + cot2 π/4
Answer:
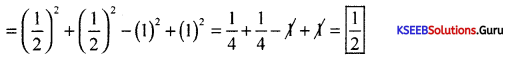
Question 25.
Find the distance between the parallel lines. 3x + 4y + 5 = 0 and 6x + 8y + 20 = 0.
Answer:
d = \(\left|\frac{C_{1}-C_{2}}{\sqrt{a^{2}+b^{2}}}\right|=\left|\frac{5-20}{\sqrt{(3)^{2}+(4)^{2}}}\right|=\left|\frac{-15}{5}\right|\) = 3
PART-C
III. Answer any ten questions. (10 × 3 = 30)
Question 26.
Prove that \(\sqrt{3}\) is an irrational number.
Answer:
If \(\sqrt{3}\) in an rational no.
∴ \(\sqrt{3}\) = \(\frac{p}{q}\),p.q ∈ z, q ≠ u
i.e., p and q do not have any common factor
Squaring on both side
∴ \(\sqrt{3}\) = \(\frac{p}{q}\)
∴ p2 – 3q2 ⇒ 3 divide p2
⇒ 3 divide p …(1)
Let p = 3k (k∈z, k ± 0)
(3k)2 = 3q2
q2 = 3k2 ⇒ 3 divide q2
⇒ 3 divide q …(2)
From (1) and (2) p and q have a common factor
This is a contradiction to the assumption
∴ \(\sqrt{3}\) is irrational
![]()
Question 27.
If A = {1, 2} B = {2, 3} C = {3, 4} Find (A × B) ∩ (A × C).
Answer:
A × B = {(1,2). (1,3), (2,2), (2,3),}
A × C= {(1,3),(1,4),(2,3),(2,4),}
(A × B) ∩ (A × C) = {(1, 3), (2, 3)}
Question 28.
Solve 32x – 10 × 3x + 9 = 0
Answer:
Let 3x = a ⇒ (3x)2 = a2
⇒ 32x = a2
∴ a2 – 10a + 9 = 0
a2 – 9a – a + 9 = 0
a(a – 9) – 1 (a – 9) = 0
(a – 9)(a – 1) = 0
a – 1 = 0
a – 9 = 0
a = 1
a = 9
3x = 30 3x = 32
x = 0
x = 2
Question 29.
Prove that log4 8 × log2 32 × log16 4 = \(\frac{15}{4}\)
Answer:
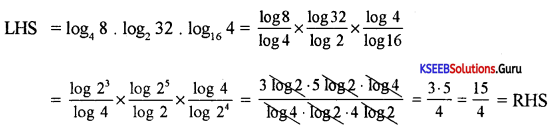
Question 30.
Insert 4 arithmetic means between 5 and 10.
Answer:
Let 5, a1, a2, a3, a4, 10
a = 5
d = ?
h = 0
a6 = 10
a6 = a + 5d
10 = 5 + 5 d
5 = 5d
d = 1
∴ a1, a2, a3 and a4 are 6, 7, 8 & 9
Question 31.
Divide Rs. 1600 between s, y and z so that y may have Rs. 100 more than x and z may have Rs. 200 more than y.
Answer:
Assume x = ₹ a
∴ y = (100 + a) ₹
2 = (200+ 100 +a) ₹
Given x + y + z = 1600
a = (100 + a) + (300 + a) = 1600
3a + 400 = 1600
3a = 1200
∴ a = ₹ 400
∴ x = ₹ 400,
y = ₹ 500,
z = ₹ 700,
![]()
Question 32.
Solve the inequality 3x + 2y > 6 graphically.
Answer:
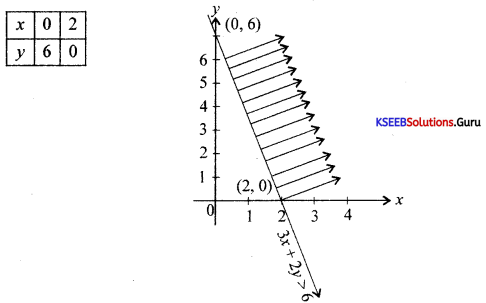
Question 33.
Preritha bought a car for Rs. 4,00,000 if it depreciates at the rate of 12% p.a. how much will it be worth after 10 years?
Answer:
Given p = ₹ 4,00,000, n= 10 year, i = \(\frac{12}{100}\) = 0.12 A=?
Formula A = p[1 – i]n
= 4,00,000 [1 – 0.12]10
= 4,00,000 (0.88)10
= 4,00,000 x
= ₹ 1,11,400.39.
Question 34.
The average weight of a group of boys and girls is 38 kg. The average weight of the boys is 42 kg and that of the girls is 33 kg. If the number of boys is 25. Find the number of girls.
Answer:
Let the no. of girls be = x
∴ combined average weight boys and girls = \(\frac{(42 \times 25)+(33 \times x)}{25+x}\)
38 = \(\frac{1050+33 x}{25+x}\)
38(25 + x) = 1050 + 33x
38x – 33x = 1050 – 950
5x = 100
x = 20 girls
Question 35.
A man buys an article at (3/4)th of its cost price and sells it for 20% more than its cost price. What is his profit percentage?
Answer:
Let the Actual price = ₹ 100
Cost price = \(\frac{3}{4}\) × 100 = ₹ 75
20% profit of SP= 120
∴ profit = (120 -75) = 45
∴ profit % = \(\frac{\text { Profit }}{\mathrm{CP}}\) × 100 = \(\frac{45}{75}\) × 100 = 60%
![]()
Question 36.
Find the value of 3 tan2 30° + \(\frac{4}{3}\)cos2 30°-\(\frac{1}{2}\)cot2 45°- \(\frac{2}{3}\)sin2 60° + \(\frac{1}{8}\)sec4 60°
Answer:
\(3\left(\frac{1}{\sqrt{3}}\right)^{2}+\frac{4}{3}\left(\frac{\sqrt{3}}{2}\right)^{2}-\frac{1}{2}(1)^{2}-\frac{2}{3}\left(\frac{\sqrt{3}}{2}\right)^{2}+\frac{1}{8}(2)^{4}\)
= \(3 \cdot \frac{1}{3}+\frac{4}{3} \cdot \frac{3}{4}-\frac{1}{2}(1)-\frac{2}{3} \cdot \frac{3}{4}+\frac{1}{8}(16)\)
= 1 + 1 – \(\frac{1}{2}\) – \(\frac{1}{2}\) + 2 = 4 – 1 = 3
Question 37.
A point P which moves such that (PA)2 = 3(PB)2 If A = (5, 0). Find the equation of the locus of P.
Answer:
Let p = (x, y) Given PA2 = 3PB2
(x – 5)2 + y2 = 3[(x + 5)2 + y2]
x2 + 25 – 10x + y2 = 3 (x2 + 25 + 10x = y2)
x2 + 25 – 10x + y2 = 3x2 + 75 + 30x + 3y2
2x2 + 2y2 + 40x + 50 = 0
x2 + y2 + 20x + 25 = 0
this is the equation of the locus.
Question 38.
Find the equation of the line passing through (5,2) and cutting off intercepts that are equal in magnitude but opposite in sign.
Answer:
By intercept form of the equation of like
\(\frac{x}{a}+\frac{y}{b}\) = 1 ……(1)
Given b = -a and (x, y) = (5, 2)
∴ (1) becomes
\(\frac{5}{a}+\frac{2}{-a}\) = 1
∴ \(\frac{5-2}{a}\) = 1
∴ a = 3, b = -3
∴ (1) becomes
\(\frac{x}{3}+\frac{y}{-3}\) = 1
x – y – 3 = 0 equation of the required line
Part -D
IV. Answer any SIX questions. (6 × 5 = 30)
Question 39.
Out of 50 people, 20 people drink tea, 10 take both tea & coffee. How many take at least one of the two drinks?
Answer:
n(T) = 20, n(C) = ? n(T ∩ C) = 10 n(T ∪ C) = 50
50 = 20 + n(C) – 10
∴ n(C) = 40
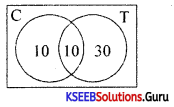
∴ no. of people taking atleast one of the two drinks
n(only T) = 10 Total = 40
n(only C) = 30
Question 40.
Evaluate \(\frac{0.5679 \times 0.0789}{0.0073 \times 0.123}\)
Answer:
Let x = \(\frac{0.5679 \times 0.0789}{0.0073 \times 0.123}\)

![]()
Question 41.
Find the sum of n terms of a GL P. 5 + 55 + 555 + …………
Answer:
5 + 55 + 555+ …………….
Let Sn = 5+ 55 + 555 +……….. n terms
Sn = 5(1 + 11 + 111 +…………)
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = 1 + 11 + 111 +…………..
Multiply both the sides by 9,
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = 9 + 99 + 999 +……….
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = (10 – 1) + (102 – 1) + (103 – 1) + ………..
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = (10 + 102 + 103 + …………..) – (1 + 1 + 1 + ………)
\(\frac{9 S_{n}}{5}=\frac{10\left(10^{n}-1\right)}{10-1}\) – n
\(\frac{9 S_{n}}{5}=\frac{10\left(10^{n}-1\right)}{9}\) – n
Sn = \(\frac{5}{9}\left[\frac{10\left(10^{\mathrm{n}}-1\right)}{9}-\mathrm{n}\right]=\frac{5}{9}\left[\frac{10}{9}\left(10^{\mathrm{n}}-1\right)-\mathrm{n}\right]\), n ∈N
Question 42.
Find the integral root between -3 and 3 by inspection and then using synthetic division. Solve the equation x3 – 2x2 – 5x + 6 = 0.
Answer:
Given p(x) = x2 – 2xz – 5x + 6
Put x = -2
∴ p(-2) – (-2)3 – 2(-2)2 – 5(-2) + 6 = – 8 – 8 + 10 + 6 = 0
By synthetic division
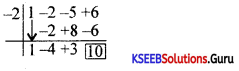
∴ x2 – 4x + 3 = 0 ⇒(x – 3)(x – 1) = 0
∴ x = 3 & 1
∴ x = 1, -2, 3
Question 43.
A sum of money amounts to Rs. 19,500 in 5 years and Rs. 22,200 after 8 years at the same rate of simple interest. Find the principal and the rate of interest.
Answer:
Principle = P = ? T1 = 5 yrs, R1 = R, A1= ₹ 19.500
T2 = 8 yrs, R2 = R, A2 = ₹ 22.200
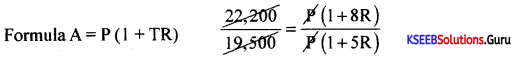
74(1 + 5R) = 65 (1 + 8R)
74+ 370 R = 65 + 520R
74 – 65 = 520R – 370R
∴ 9 = 150R
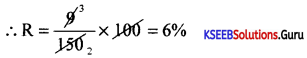
R = 6%
Substitute
19,500 = P(1 + 5 × 0.06)
∴ P = ₹15,000
![]()
Question 44.
If Poornima deposits Rs. 600 at the beginning of every year for the next 15 years. Then how much will be accumulated at the end of 15 years if the interest rate is 7% p.a?
Answer:
a = ₹600, n = 15 yrs, i = 7% = 0.07, F = ?
F = \(\frac{a\left[(1+i)^{n}-1\right]}{i}\)(1 + i)
= \(\frac{600\left[(1.07)^{15}-1\right]}{0.07}\)(1 + 0.07)
= \(\frac{600[2.759-1]}{0.07}\)(1.07)
= \(\frac{600 \times 1.759 \times 1.07}{0.07}\) = ₹16,132.54
Question 45.
The price of a pair of trousers was decreased by 22% to Rs. 390 what was the original price of the trouser?
Answer:
Let the original price = ₹ x
then (x – \(\frac{22}{100}\)x) = 390
x(1 – \(\frac{22}{100}\)) = 390
x(\(\frac{78}{100}\)) = 390
x = \(\frac{390 \times 10}{78}\) = ₹500
Question 48.
If θ = \(\frac{5}{2}\) and θ is acute then prove that \(\frac{3 \cos \theta+2 \sin \theta}{3 \cos \theta-4 \sin \theta}=\frac{19}{7}\)
Answer:
\(\left[\frac{3 \cos \theta+2 \sin \theta}{3 \cos \theta-4 \sin \theta}\right]\) + by sinθ
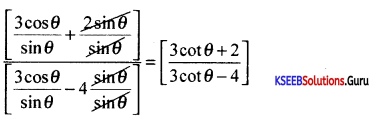
∴ put cot θ = \(\frac{5}{2}=\left[\frac{3(5 / 2)+2}{3(5 / 2)-4}\right]=\left[\frac{15+4}{15-8}\right]\) = \(\frac{19}{7}\)
Question 47.
Show that the following points are the vertices of a square A (1, 1) B(4, 1), C(4, 4), D(l,4)
Answer:
AB = \(\sqrt{(1-4)^{2}+(1-1)^{2}}=\sqrt{(-3)^{2}}\) = 3
BC = \(\sqrt{(4-4)^{2}+(1-4)^{2}}=\sqrt{(-3)^{2}}\) = 3
CD = \(\sqrt{(4-1)^{2}+(4-4)^{2}}=\sqrt{3^{2}}\) = 3
AD = \(\sqrt{(1-1)^{2}+(1-4)^{2}}=\sqrt{(-3)^{2}}\) = 3
∴ AB = BC = CD = AD = 3A. ABCD forms and equal.
Question 48.
Find ‘a’ so that the lines x – 6y + a = 0,2x + 3y + 4 = 0 and x + 4y + 1 = 0 are concurrent.
Answer:
2x + 3y + 4 = 0 …(1)
x + 4y +1 = 0 xly by 2
2x + 8y + 2 = 0 …(1)
(1) – (3) -5y + 2 = 0
∴ y = 2/5 in (1)
2x + 3(215) + 4 = 0
∴ 2x = –\(\frac{6}{5}\) – 4 = –\(\frac{26}{5}\)
Substitute x – 6y + a = 0
∴ a = \(\frac{13}{5}+\frac{12}{5}\) = 5
–\(\frac{13}{5}\) – 6(\(\frac{2}{5}\)) – a = 0
∴ a = 5
Part-E
V. Answer any ONE question. (1 × 10 = 10)
Question 49.
(a) If U = {1,2,3,4,5,6,7,8,9} A = {1,2,3,4,5} B = {3,4,5,6,7} show that (A∩B)’ = A’ ∪ B’.
Answer:
(a) A∩B = {3,4,5} A’ = {6,7,8,9}
B’ = {1,2,89}
LHS= (A∩B)’ = {3,4, 5}’ = {1,2,6, 7,8,9}
RHS = A’∪B’ = {6,7,8,9}∪{1, 2, 8, 9} = {1, 2, 6, 7, 8, 9}
∴ LHS = RHS
(b) Insert 3 Geometric means between and \(\frac{1}{4}\) and \(\frac{1}{64}\)
Answer:
\(\frac{1}{4}\), g1, g2, g3, \(\frac{1}{64}\)
3 Gm’n = g1, g2, and g3
a = \(\frac{1}{4}\) formula an = a.rn-1
a5 = \(\frac{1}{64}\)
n = 5
r = ?
\(\frac{1}{64}=\frac{1}{4}\) x r5-1
\(\frac{1}{16}\) = r4
∴ r = \(\frac{1}{2}\)
∴ g1 = ar = \(\frac{1}{4} \times \frac{1}{2}=\frac{1}{8}\)
g2 = ar2 = \(\frac{1}{4} \times \frac{1}{4}=\frac{1}{16}\)
g3 = ar3 = \(\frac{1}{4} \times \frac{1}{8}=\frac{1}{32}\)
(c) Find the L.C.M of \(\frac{1}{3}, \frac{5}{6}, \frac{5}{7}\)
Answer:
\(\frac{\mathrm{HCF} \text { of } \mathrm{Nr}}{\text { Lem of Dr }}=\frac{1}{42}\)
![]()
Question 50.
(a) A manufacture produces and sells balloons at Rs. 8 / unit His fixed cost is Rs. 6500 and the variable cost/balloon is Rs. 3.20 calculate.
(i) Revenue function
(ii) Cost function
(iii) profit function
(iv) Revenue at BEP
Answer:
(i) Revenue function = R(x) = Price × Quantity = 8x Quantity = x unit
(ii) Cost function : C(x) = TVC + TFC = 3.5x + 6500
(iii) Profit function : P(x) = R(x) – C(x)
= 8x – (3.5x + 6500)
= 4.5x – 6500
(iv) Revenue B ∈ P
R(x) = C(x)
4.5x – 6500 = 0
x = \(\frac{6500}{4.5}\) = 1445 unit
(b) Find the foot of the perpendcular drawn from the point (-2, -1) on the line 3x- + 2y-5 = 0.
Answer:
Let P(x1, y1) = (-2, -1) given pt.
Q (h, k) be the Foot of ⊥r to the line ax + by+ 1 = 0
Formula
\(\frac{h-x_{1}}{a}=\frac{x-y_{1}}{b}=\frac{-\left(a x_{1}+b y+1\right)}{a^{2}+b^{2}}\)
a = 3, b = 2, c = 5, (x1, y1) = (-2, -1)
\(\frac{h-(-2)}{3}=\frac{k-(-1)}{2}=\frac{-[3(-2)+2(-1)-5]}{3^{2}+2^{2}}\)
\(\frac{h+2}{3}=\frac{k+1}{2}=\frac{-(-6-2-5)}{13}\)
∴ \(\frac{h+2}{3}\) = + 1
\(\frac{k+1}{2}\) = + 1
∴ h = 1
k = 1
∴ (h, k) = (1, 1)
(c) Find the equation of the locus of the point which moves such that it is equidistant from (4, 2) and the x-axis.
Answer:
Let p(x, y) be a locus
pt-A(4, 2) x-axis B(x, 0)
Given PA = PB
\(\sqrt{(x-4)^{2}+(y-2)^{2}}=\sqrt{(x-x)^{2}+(y-0)^{2}}\)
(x – 4)2 + (y – 2)2 = y2
