Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2018 (North), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2018 (North)
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART-A
I. Answer any TEN questions. (10 × 1 = 10)
Question 1.
Write the imaginary part of the complex number -3i + 7
Answer:
-3.
Question 2.
If (2x + 4, 0) = (8,0) find x.
Answer:
2x + 4 = 8
2x = 4
x = 2
Question 3.
Simplify: \(\left(\frac{9}{4}\right)^{-3 / 2}\)
Answer:
\(\left[\left(\frac{3}{2}\right)^{2}\right]^{-3 / 2}=\left(\frac{3}{2}\right)^{-3}=\left(\frac{2}{3}\right)^{3}=\frac{8}{27}\)
Question 4.
Express 34 = 81 in logarithmic form.
Answer:
log381 = 4
Question 5.
Find the tenth term of HP \(\frac{1}{2}, \frac{1}{4}, \frac{1}{6}\)………..
Answer:
AP → 2, 4, 6,…. T10 = 2 + (n – 1)2 = 2 + 2n – 2 = 2n = 2(10) = 20
∴ The tenth term of HP = \(\frac{1}{20}\)
![]()
Question 6.
Form the cubic equation whose roots are 3, 5, 7.
Answer:
(x – 3)(x – 5) (x – 7) = 0
(x – 3)(x2 – 5x – 7x + 35) = 0
(x – 3)(x2 -12x + 35) = 0
x3 – 12x2 + 35x – 3x2 + 36x – 105 = 0
x3 – 15x2 + 71x – 105 = 0
Question 7.
What is the simple interest for 245 days for ₹ 6000 at 8% p.a simple interest?
Answer:
SI = 6000 × \(\frac{245}{365} \times \frac{8}{100}\) = 402.39
Question 8.
What is the present value of a perpetuity of 5000 at 8% p.a
Answer:
A = \(\frac{A}{r}=\frac{5000}{0.08}\) = 62,500
Question 9.
If the cost price of an item is 25000 and the profit is 10,000 find the profit percentage.
Answer:
CP = 25,000 profit = ₹ 10,000
Profit% = \(\frac{\text { Profit }}{\mathrm{CP}}\) × 100 = 40%
Question 10.
Express 144° ¡n radian measure.
Answer:
\(\frac{144 \times \pi}{180}=\frac{4 \pi}{5}\)
![]()
Question 11.
Find the value of cos 1500
Answer:
cos150 = cos(180 – 30) = -cos 30 = \(\frac{\sqrt{3}}{2}\)
Question 12.
Find k if the slope of the line joining the points (2,5) and (k, 13) is 20.
Answer:
\(\frac{13-5}{k-2}\) = 20 ⇒ \(\frac{8}{k-2}\) = 20 ⇒ 8 = 20k – 40 ⇒ 20k = 48 ⇒ k = \(\frac{48}{20}=\frac{12}{5}\)
Part-B
II. Answer any TEN questions. (10 × 2 = 20)
Question 13.
Find the sum of all positive divisors of 768.
Answer:

768 = 28 × 31
= p1α1 × p2α2
p1 = 2 p2 = 3
α1 = 8, α2 = 1
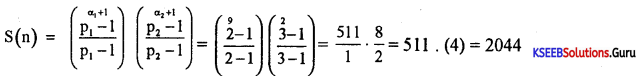
Question 14.
Find the least integer which when divided by 36,40 and 48 leaves the same remainder 5.
Answer:
LCMof 36, 40, 48
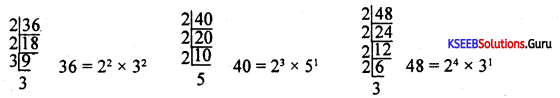
LCM = 24 × 32 × 51 = 16 × 9 × 5 = 720
∴ Required member = 720 + 5 = 725
Question 15.
Find the domain and range of relation R = {(1, 2) (2, 5) (1, 6) (3, 6)}
Answer:
Domain = {1, 2,3)
Range = {2, 5, 6}
![]()
Question 16.
If ax = by = cz and b2 = ac show that \(\frac{1}{x}+\frac{1}{z}=\frac{2}{y}\)
Answer:
Let ax = by = cz = k (say)
∴ ax = k ⇒ a = k1/x, by = k ⇒ b = k1/y, cz = k ⇒ c = k1/z
Now, b2 = ac
∴ (k1/y)2 = k1/x. k1/z
∴ k2/y = k1/x+1/z
Bases are the same ∴ Equating powers on both sides, we get.
\(\frac{1}{x}+\frac{1}{z}=\frac{2}{y}\)
Question 17.
If the second term of the GP is 6 and fifth term is 162 then find the GP.
Answer:
T2 = 6, T5 = ar4 = 162 ar = 6 ar4 = 162
ar.r3 = 162
6r3 = 162
r3 = \(\frac{162}{6}\) = 27
r = 3
Question 18.
The sum of three consecutive numbers is 243. Find the three numbers.
Answer:
x + x + 1 + x + 2 = 243
3x + 3 = 2433x = 240
x = 80
80, 81, 82
Question 19.
If a and P are the roots of the equation 2x2 + 4x + 1 = 0 find the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\)
Answer:
α + β = –\(\frac{4}{2}\) = -2
\(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\alpha+\beta}{\alpha \beta}\)
αβ = \(\frac{c}{a}=\frac{1}{2}=\frac{-2}{\frac{1}{2}}\) = -4
Question 20.
Solve 7x + 3 < 5x + 9, x ∈ R and represent on the number line.
Answer:
![]()
Question 21.
Find the future value of an annuity of ₹ 5000 at 12% p.a for 6 years.
Answer:
A = Rs.5,000 r = 0.12 n = 6
F = \(\frac{A\left[(1+r)^{n}-1\right]}{r}=\frac{5000\left[(1+0.12)^{6}-1\right]}{0.12}=\frac{4869.11}{0.12}\) = 40,575.9
Question 22.
Prove that (1 + cotA)2 + (1 – cotA)2 = 2 cosec2A
Answer:
![]()
Question 23.
Find the value of cos 60° -sin 30° – cot3 45°
Answer:
\(\frac{1}{2}-\frac{1}{2}\) – (1)3 = -1
Question 24.
Find the distance of the centroid of the triangle formed by the points (7, 1) (1, 5) and (1, 6) from origin.
Answer:
G = \(\left[\frac{7+1+1}{3}, \frac{1+5+6}{3}\right]\) = (3, 4)
O = (0, 0)
OG = \(\sqrt{(3)^{2}+(4)^{2}}=\sqrt{9+16}=\sqrt{25}\) = 5
Question 25.
Find the equation of the locus of the point which moves such that it is equidistant from (4,2) and the X – axis.
Answer:
P = (x, y) distance from x – axis = y A = (4,2)
PA = y
\(\sqrt{(x-4)^{2}+(y-2)^{2}}\) =y
(x-4)2 + (y-2)2 = y2
x2 – 8x + 16 – 4y + 4 = 0
Part-C
III. Answer any TEN questions. (10 × 3 = 30)
Question 26.
Prove that \(\sqrt{2}\) is an irrational number.
Answer:
We shall prove it by the method ofcontradiction.
If possible Let \(\sqrt{2}\) be a rational number
Let \(\sqrt{2}\) = \(\frac{p}{q}\) where p and q are Integers and q ≠ 0.
Further let p and q are coprime i.e. H.C.F. of p and q = 1.
\(\sqrt{2}\) = \(\frac{p}{q}\) ⇒ \(\sqrt{2}\)q = p
⇒ 2q2 = p2
⇒ 2 divides p2 ⇒ 2 divides p
⇒ p is even
Let p = 2k where k is an integer p2 = 4k2
2q2 = 4k2
q2 = 2k2 ⇒ q2 is even
⇒ q is even.
Now p is even and q is even which implies p and q have a common factor 2. which is a
contradiction of the fact that p and q are co-prime.
∴ our assumption that \(\sqrt{2}\) is rational is wrong and hence \(\sqrt{2}\) is irrational.
![]()
Question 27.
A relation R is defined on the set of integers by
R = {(X, Y): X-Y is a multiple of 5} Show that R is an equivalence relation on Z.
Answer:
x – x = 0 is a multiple of 5
∴ (x, x) ∈ R ∀ x
R is reflexive
Let (x, y) ∈ R
x – y is a multiple of 5
y – x is a multiple of 5 (y, x) ∈ R
∴ R is symmetric
Let (x, y) ∈ R
(y, z) ∈ R
x -y is a multiple of 5 and y – z is a multiple of 5
(x – y) +(y – z) is a multiple of 5
x-z is a multiple of 5 (x, z) ∈ R
∴ R is transitive
R is an equivalence relative
Question 28.
Solve : 32x – 10.3x + 9 = 0
Answer:
Let 3x = a ⇒(3x)2 = a2
⇒ 32x = a2
∴ a2 – 10a + 9 = 0
a2 – 9a – a + 9 = 0
a(a – 9) -1 (a – 9) = 0
(a – 9)(a – 1) = 0
a – = 0 a – 9 = 0
a = 1 a = 9
3x = 30 3x = 32
x = 0 x = 2
Question 29.
If x2 + y2 = 12xy, show that 2 log (x – y) = log2 + log 5 + log x + log y.
Answer:
x2 + y2 = 12xy
x2 + y2 – 2zy = 12xy – 2xy ⇒ (x – y)2 =10xy
log(x-y)2 = log10xy
2 log (x – y) = log 10 + log x + log y
2 log (x – y) = log (2 x 5)+log x + log y
2 log (x – y) = log 2 + log 5 + log x + logy
Question 30.
Insert 4 Arithmetic means between 14 and 34.
Answer:
14, a1, a2, a3, 34
a = 14
T =34
n = 5
Tn = a + (n-1)d
3 = 14 + (4 )d
20 = 4 d
d = 5
14, 19, 24, 29, 34
Question 31.
A number consists of 2 digits whose sum is 4, if 18 is added to the number, the digits get interchanged. Find the number.
Answer:
Let the digit in the tens place be x and the digit in the unit place be y
The nunter is 10x + y
Given x + y = 4 …………(1)
Also given 10x + y + 18 = 10y + x
10x – x + y – 10y + 18 = 0
9x – 9y + 18 = 0
x – y + 2 = 0
x – y = -2……………..(2)
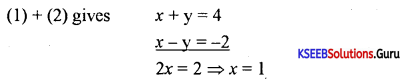
x + y = 4
y = 4 – x = 4 – 1 = 3
The numbcr is 10x + y
10(1) + 3 = 10 + 3 = 13
The number is 13.
Question 32.
Solve graphically: 2x + y ≥ 8 ; and x + y ≥ 110
Answer:
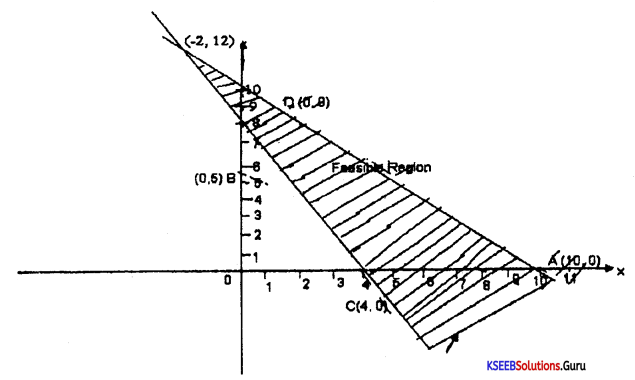
Question 33.
Preitha bought a car for ₹ 4,00,000. If it depreciates at the rate of 12% per year, how much will it be worth after 10 years?
Answer:
C = Rs.4,00,000 r = 12% = 0.12 n = 10
B = C(1 – r)n
= 4,00,000 (1 – 0.12)10 = 4,00,000 (0.88)10
B = Rs. 1,11,400.39
Question 34.
The average age of 10 students in a class increases by 4.8 months, when a boy of 6 years is replaced by a new boy. What is the age of the new boy?
Answer:
Let the average age of 10 students x
∴ Sum of ages of 10 students = 10x
A boy of 6 years is replaced by a new boy whose age is y
∴ Total age of 10 students 10x + y – 6
∴ Average age of 10 students = \(\frac{10 x+y-6}{10}\)
∴ \(\frac{10 x+y-6}{10}\) = x + \(\frac{4.8}{12}\) 4.8 months = \(\frac{4.8}{12}\) years
x by 10
∴ 10x + y – 6 = 10x + \(\frac{48}{12}\)
![]()
y = 6 + 4 = 10
∴ Age of the new boy = 10 years
![]()
Question 35.
In a dance competition, 70% of the participants were girls. 35% of the boys and 65% of the girls are selected for the next round. If 49 girls were eliminated, And the number of boys who got selected.
Answer:
Let the total number of participants – x
If 65% of girls got qualified then 35% of girls got eliminated
Total number of girls = \(\frac{70}{100}\)x = 0.7x
Total number of boys = \(\frac{30}{100}\) × x = 0.3x
∴ total girls eliminated = \(\frac{35}{100}\) × 0.7x = 0.245x
Hence 0.245x = 49
x = \(\frac{49}{0.245}\)= 200
Hence total number of boys eliminated = \(\frac{35}{100}\) × 0.3 × 200 = 21
Question 36.
If tan A = \(\frac{-12}{5}\) and 270% < A < 360° find the value of \(\frac{3 \sin A-2 \cos A}{9 \cos A+4 \sin A}\)
Answer:
\(\frac{3 \sin A-2 \cos A}{9 \cos A+4 \sin A}=\frac{3\left(-\frac{12}{13}\right)-2\left(\frac{5}{13}\right)}{9\left(\frac{5}{13}\right)+4\left(\frac{-12}{13}\right)}=\frac{-36-10}{45-48}=\frac{-46}{-3}=\frac{46}{3}\)
Question 37.
Find area of the triangle whose vertices are A(6, 3) B(-3, 5) C(4, -2)
Answer:
A = (6,3) B = (-3,5) C = (4, -2)
∆ABC = \(\frac{1}{2}\)[x1(y2 – y3) + x3 (y3 – y) + X3 (y1 – y2)]
= \(\frac{1}{2}\) [6 (5 + 2) – 3 (-2 – 3) + 4 (3 – 5)] = \(\frac{1}{2}\) [6(7) – 3(-5) + 4(-2)]
= \(\frac{1}{2}\) [42 + 15 – 8] = \(\frac{1}{2}\) [49] squarts
![]()
Question 38.
Find the equation of the line passing through (5,2) and cutting off intercepts that are equal in magnitude but opposite in sign.
Answer:
b = -a \(\frac{x}{a}+\frac{y}{-b}\) = 1 put x = 5, y = 2\(\frac{5}{a}-\frac{2}{a}\) = 1
3 = a, b = -3
∴ \(\frac{x}{3}+\frac{y}{-3}\) = 1 ⇒ \(\frac{x-y}{3}\) = 1 ⇒ x – y – 3 = 0
Part – D
Answer any SIX questions. (6 × 5 = 30)
Question 39.
In a class of 250 students if 75 students have taken statistics and 25 have taken both statistics and economics and 100 have taken neither statistics nor economics. Find how many have taken
(a) economics (b) economics only Also represent in Venn diagram.
Answer:
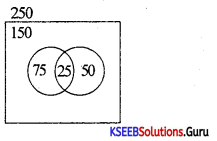
n(S∪E) = 250 – 100 = 150
n(S) = 75, n(S ∩ E) = 25
n(S ∪ E) = n(S) + n(E) – n(S ∩ E)
150 = 75 + n(E) – 25
150 = n(E)
n(E)= 100 → Economics
n(E – S) = n(E) – n[E ∩ 5) = 100 – 25 = 75 →Economics only
Question 40.
Evaluate using log \(\frac{0.5634 \times 0.0635}{2.563 \times 12.5}\)
Answer:
Let x = \(\frac{0.5634 \times 0.0635}{2.563 \times 12.5}\)
log x = log[latex]\frac{0.5634 \times 0.0635}{2.563 \times 12.5}[/latex]
= log 0.5634 + log 0.0635 – log 2.563 – log 12.5
=1.7508 + 2.8028-0.4087-1.0969
= 2.5536- 1.5056 = 2 + 0.5536-1.5056
= -2 – 0.952 = -2.952
= -3 + 3 -2.952 = – 3 + 0.048 = 3.048
![]()
Question 41.
Find the sum of all integers between 200 and 500 which are divisible by 7.
Answer:
Sn = 203 + 210 + 217 +………….+ 497 a = 203, d = 7, T = 497 , n = ?
Tn = a + (n – 1)d
497 = 203 + (n- 1)7
497 = 203 + 7n-7
497= 196 +7n
7n = 301
n = 43
Sn = \(\frac{n}{2}\)(a + Tn) = \(\frac{43}{2}\)(203 + 497) = 15,050
Question 42.
Find an integral root between -3 and 3 by inspection and they using synthetic division solve the equation x3 – 10x2 + 29x – 20 = 0
Answer:
Put x = 1
1 – 10(1)2 + 29(1) – 20
1 – 10 + 29 – 20
30 – 30 = 0
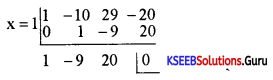
Quotient = x2 – 9x + 20
Remainder = 0
x3 – 10x2 + 29x – 20 = 0
(x + 1)(x2 – 9x + 20) = 0
x – 1, x2 – 9x + 200
x = 4, x = 5
Question 43.
A sum of money amounts to Rs. 19500 in 5 years and 22,200 after 8 years at the same rate of simple interest. Find the principal and rate of interest.
Answer:
P = ?, A = Rs.19,500, T = 5years
A = Rs.22200, T = 8years R = ?
A = P + SI
A = P + \(\frac{\mathrm{PTR}}{100}\)
19,500= P(1 + \(\frac{5 \mathrm{R}}{100}\)) ………(1)
22,220= P(i + \(\frac{8 \mathrm{R}}{100}\)) ………………(2)
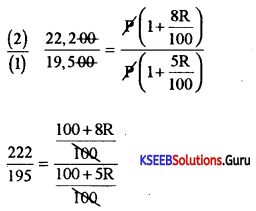
(100 + 5R)222 = (100 + 8R) 195,
22200 + 1110R = 19500 + 1560 R
22200 – 19500 = 1560 R – 1110
R = \(\frac{2700}{450}\) = 6%p.a. ∴ R = 6%p.a.
From (1)
19,500 = P(1 + \(\frac{5 \mathrm{R}}{100}\))
19500 = P(1 + \(\frac{5 \cdot 6}{100}\)) = P(1 + \(\frac{30}{100}\)) = P(1 + \(\frac{3}{10}\)) = P(\(\frac{10+3}{10}\)) = \(\frac{13}{10}\)P
P = \(\frac{19500 \times 10}{13}\) = 15,000
∴ P = Rs. 15,000
Question 44.
Find the present value of an annuity of 2000 payable at the beginning of each quarter for the next 3 years if the rate of interest is 4% p.a. compounded quarterly.
Answer:
A = Rs.2000 n = 3 x 4 = 12 r = = 0.01
P = \(\frac{A\left[(1+r)^{n}-1\right]}{r(1+r)^{n}}\)(1 + r) = \(\frac{2000\left[(1+0.01)^{12}-1\right]}{0.01(1+0.01)^{12}}\)(1 + 0.01)
= \(\frac{2000\left[(0.01)^{12}-1\right]}{0.01(1.01)^{12}}\)(1.01) = \(\frac{256.18}{0.011}\) = 23,289.09
![]()
Question 45.
A radio is sold at a profit of 25%. Cost price and selling price both are increased by 100. If the new profit is 20% find the original cost of the ratio.
Answer:
Let x be the C.P. of the radio.
then SP = \(\frac{125 \mathrm{x}}{100}\)
When CP changes to x + 100SP = \(\frac{125 \mathrm{x}}{100}\) + 100
i.e., x + 1.00 +20% of(x + 100) = \(\frac{125 \mathrm{x}}{100}\) + 100
x + 100 + \(\frac{20}{100}\)(x + 100) = \(\frac{125 x+10000}{100}\)
100x + 10000 + 20x + 2000 = 125x + 10000
5x = 2000
x = Rs.400
The original cost of the radio = Rs.400
Question 46.
Prove that \(\frac{\tan A}{1-\cot A}+\frac{\cot A}{1-\tan A}\) = 1 + sec A cosec A
Answer:

= secA.cosecA + 1 = RHS
Question 47.
Show that (-3 1), (-6, -7) (3, -9) (6, -1) taken in order are vertices of a parallelogram.
Answer:
Question 48.
Find the image of the point (2, 4) on the line x + y – 10 = 10
Answer:
Let P be the point (2,4) and Q(x,y) be its reflection on the line x + y – 10 = 0. Let PQ cut the line at R. Then R is the midpoint of PQ and PQ is perpendicular to the given line.
Now R = \(\left(\frac{x_{1}+2}{2}, \frac{y_{1}+4}{2}\right)\) Since R lies on x + y – 100
We have \(\left(\frac{x_{1}+2}{2}+\frac{y_{1}+4}{2}\right)\) – 10 = 0 i.e. x1 + y1 – 14 = 0 ………………(1)
Slope ofPQ = \(\frac{y_{1}-4}{x_{1}-2}\) Slope ofthegiven line x + y – 100 is -1.
Since PQ is perpendicular to the line x + y – 10 = 0 m1m2 = -1
Solving (1) and (2) we get the point of intersection as JC, = 6 and y] = 8 ∴Image = Q (6,8)
Part – E
V. Answer any ONE question. (1 × 10 = 10)
Question 49.
(a) If A = {1, 2, 3} B = {2, 3, 4}, C = {3, 4, 5} verify (A × B) (A × C) = A × (B ∩ C)
Answer:
A × B = {(1,2), (1,3), (1,4), (2,2), (2,3), (2,4), (3,2), (3,3), (3,4)}
A × C = {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,3), (3,4), (3,5)}
(A × B)∩(A × C) = {(1,3),(1,4),(2,3),(2,4),(3,3),(3,4)} B∩C = {3,4}
A × (B∩C) = {(1,3),(1,4),(2,3),(2,4),(3,3),(3,4)} ∴ (A × B)∩(A × C) = A × (B∩C)
(b) The daily cost of production C for x units is given by C(x) = 17.5 x + 7000.
(i) If each unit is sold for 30, then determine the minimum units that should be produced and sold to ensure no loss.
(ii) If it is known that 500 unit can be sold daily what price / unit should be charged to guarantee no loss.
Answer:
(i) C(x) = 17.5x + 7000
R(x) = 30x, R(x) = C(x)
30x = 175x + 7000,
12.5x = 7000
x = \(\frac{7000}{12.5}\) = 560 BEP
(ii) If the S.P. is reduced by Rs.3/unit then R(x) = 27x
For BEP R(x) = C(x)
27x = 17.5x + 7000,
27x – 17.5x = 7000
9.5x = 7000,
x = \(\frac{7000}{9.5}\) = 73684 = 737 units
(c) The average score of 20 boys is 60% and average score of 30 girls is 70% Find the combined averaged score.
Answer:
x1 = 60%
x2 = 70%
N1 = 20
N2 = 30
X̄ = \(\frac{\mathrm{X}_{1} \mathrm{~N}_{1}+\mathrm{X}_{2} \mathrm{~N}_{2}}{\mathrm{~N}_{1}+\mathrm{N}_{2}}=\frac{(60)(20)+(70)(30)}{(20)+(30)}=\frac{1200+2100}{50}=\frac{3300}{50}\) = 66%
![]()
Question 50.
(a) Find the sum to n terms of the series 9 + 99 + 999 + ………………….
Answer:
Sn = 9 + 99 + 999 +…………. = (10 – 1) + (102 – 1) + (103 – 1) + ………………
= (10 + 102 + 103 +………………. ) – (1 + 1 + 1 +……………. ) = \(\frac{10\left(10^{n}-1\right)}{10-1}\) – n
Sn = \(\frac{10\left(10^{n}-1\right)}{9}\) – n
n ∈ N
(b) Find k if line x – 2y + 1 = 0; 2x – 5y + 3 = 0; 5x – 9y + k = 0 are concurrent.
Answer:
(c) If the product of two numbers ¡s 216 and their LCM ¡s 36 find their HCF.
Answer:
ab = 216 LCM = 36 HCF = ?
HCF × LCM = ab = 216
HCF = \(\frac{216}{\mathrm{LCM}}\) HCF = \(\frac{216}{36}\) = 6