Students can Download 1st PUC Basic Maths Model Question Paper 5 with Answers, Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Model Question Paper 5 with Answers
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART – A
I. Answer any ten questions (10 × 1 = 10)
Question 1.
Write the canonical representation of 60.
Answer:

Question 2.
If A = {1, 2, 3}, B = {3, 4, 5, 6} find A – B.
Answer:
A – B = {1,2}
Question 3.
If f: R → R is defined by/(x) = 2x + 3 then find f(1/2).
Answer:
f(1/2) = 2 × \(\frac{1}{2}\) + 3 =1 + 3 = 4
Question 4.
Simplify : (3°)2 + (32)°
Answer:
= 12 + 9° = 1 + 1 = 2
Question 5.
Evaluate : log\(\sqrt{x}\) 4 = 2
Answer:
⇒ (\(\sqrt{2}\))2 = 4 ⇒ x = 4
![]()
Question 6.
Find the 11th term of the A.P. 3, 5, 7, 9…………
Answer:
Here a = 3, d = 5 – 3 = 2, n = 11
Tn = a + (n – 1 )d
T11 = 3 + (11 – 1)2 = 3 + (10) = 3 + 20 = 23
Question 7.
The sum of 6 times a number and 5 times the number is 55. Which is that number?
Answer:
Let the no. be x.
Given 6x + 5x =55
11x =55
x = \(\frac{55}{11}\) = 5
Hence the number is 5.
Question 8.
Convert the ratio 2: 5 into percentages.
Answer:
2:5 = \(\frac{2}{5}\) × 100% = 40%
Question 9.
Write the formula for the future value of annuity immediate.
Answer:
F = \(\frac{\mathrm{A}\left[(1+r)^{n}-1\right]}{r}\)
Question 10.
Convert 225° into radians.
Answer:
225° = 225 × \(\frac{\pi}{180}=\frac{5 \pi}{4}\)
![]()
Question 11.
The average age of 10 girls ¡n a class in 17 years. What is the sum of their ages?
Answer:
Sum of their ages 10 × 17 = 170 years.
Question 12.
Find the slope of the line 3x + 4y – 29 = O
Answer:
Slope = \(\frac{-a}{b}=\frac{-3}{4}\)
PART-B
Answer any Ten questions. (10 × 2 = 20)
Question 13.
Find the real part of \(\frac{1+2 i}{3-4 i}\)
Answer:
\(\frac{1+2 i}{(3-4 i)} \times \frac{(3+4 i)}{(3+4 i)}=\frac{(1+2 i)(3+4 i)}{9+16}=\frac{(3-8)+i(10)}{25}=\frac{-5+10}{25}=-\frac{1}{5}+\frac{2 i}{5}\)
Real part = –\(\frac{1}{5}\) Imaginary part = \(\frac{2}{5}\)
Question 14.
Let f = {(1, 2), (2,3), (3, 4)} be a function from 2 to 2 where z is the set of integers defined by/W = ax + b v some integers a and b. Determine a and b.
Answer:
2 = a + b …(i) 3 = 2a + b …………. (ii)
equation (1) and (2)
-1 = -a
∴ a = 1 ∴ b = 1
Question 15.
Solve : 32x – 10. 31 + 9 = 0.
Answer:
32x – 10. 3x + 9 = 0
Let 3x = a ⇒ (3x)2 = a2
⇒ 32x = a2
∴ a2 – 10a + 9 = 0
a2 – 9a – a + 9 = 0
a(a – 9) -1 (a – 9) = 0
(a – 9) (a – 1) = 0
a – 1 = 0
a – 9 = 0
a = 1 a = 9
3x = 3°
3x = 32
x = 0 x = 2
Question 16.
Prove that loga mn = loga m + loga n
Answer:
Let loga m=x ⇔ ax = m
loga n = y ⇔ ay = n
loga mn = z ⇔ az = mn
Consider az = mn ⇔ az = ax.ay ⇒ az = ax+y ⇒ z = x + y ⇒ loga mn = loga m + loga n
Question 17.
If \(\frac{3}{5}\), K, \(\frac{13}{5}\) are inA.P., then find the value of K.
Answer:
k – \(\\frac{3}{5}=\frac{13}{5}\) – k
k + k = \(\frac{13}{5}+\frac{3}{5}=\frac{16}{5}\)
2k = \(\frac{16}{5}\) ⇒ k = \(\frac{8}{5}\)
Question 18.
Form cubic equation whose roots are 3, 5, 7
Answer:
3, 5, 7 are the roots
∴ x – 3, x – 5, x – 7 are the factors
Equation is (x – 3) (x – 5) (x – 7) = 0
⇒ x3 – 15x2 + 71x – 105 = 0
![]()
Question 19.
Solve 3x – 4 > 7 – 2x (x∈R)
Answer:
3x – 4 > 7 – 2x
3x + 2x > 7 + 4
5x > 11
x > \(\frac{11}{5}\) or x ∈ (\(\frac{11}{5}\), ∞)
Question 20.
Find the simple interest on Rs. 800 at 8% p.a. for one year one month and 10 days.
Answer:
P = 800. R = 8 T = 1yr, I month and 10 days
T = (1 + \(\frac{1}{12}+\frac{10}{365}\))years (1 + 0.08 + 0.02)(1.1)year
SI = \(\frac{\mathrm{PTQ}}{100}=\frac{800 \times 8 \times 1.1}{100}\) = 71.11
Question 21.
Find the effective rate of interest when a sum lent at 12% is computed half yearly.
Answer:
R = Nominal rate of interest = 12% = \(\frac{12}{100}\) = 0.12
q = number of times interest is compounded in one year = 2
r = effective rate of interest
= \(\left(1+\frac{R}{q}\right)^{q}\) – 1 = \(\left(1+\frac{0.12}{2}\right)^{2}\) – 1 = (1 + 0.6)2 – 1 = (1.06)2 – 1 = 1.1236 – 1
= 0.1236 = 12.36%
∴ Effective rate of interest = 12.36%
Question 22.
Find the present value of a perpetuity of Rs.3000 to be received forever at 4% p.a.
Answer:
A = Rs.3000 r = 0.04
P∞ = \(\frac{\mathrm{A}}{\mathrm{r}}=\frac{3000}{0.04}\) = 75,000
Question 23.
The average mark of is students in a class is 45. A student who has scored 50 marks leaves the classroom. Find the average marks of the remaining 14 students.
Answer:
n= 15, x̄ =45, Σx = nx̄ = 15(45) = 675
Total marks of 14 students = 675 – 50 = 625
Average marks of 14 students = \(\frac{625}{14}\) =44.6
Question 24.
The angles of a triangle are in the ratio 3:4:5. Find them in radians and in degrees.
Answer:
3:4:5 or 3x, 4x, 5x
3x + 4x + 5x = 180°, 12x = 180
x = \(\frac{180}{12}\) = 15°
Angles are 3(15°), 4(15°), 5(15°)
45°, 60°, 75°,
45° = 45 × \(\frac{\pi}{180}=\frac{\pi}{4}\)
60° = 60 × \(\frac{\pi}{180}=\frac{\pi}{3}\)
75° = 75 × \(\frac{\pi}{180}=\frac{5 \pi}{12}\)
![]()
Question 25.
If the distance between (2, a) and (-1, 1) is \(\sqrt{13}\) find the value of a
Answer:
Let A = (2, a) B = (-1, 1)
∴ AB = \(\sqrt{(2+1)^{2}+(a-1)^{2}}\)
i.e \(\sqrt{13}=\sqrt{9+(a-1)^{2}}\)
squaring
∴ 13 = 9 + (a – 1)2
∴ (a – 1)2 = 4
∴ (a – 1) = ±2
∴ a – 1 = 2 or a – 1 = -2
i.e., a = 3 or a = -1
PART-C
III. Answer any ten questions. (10 × 3 = 30)
Question 26.
Prove that 3 + \(\sqrt{5}\) is an irrational number.
Answer:
If possible let 3 + \(\sqrt{5}\) be a rational number
∴ 3 + \(\sqrt{5}\) = \(\frac{p}{q}\) where p, q ∈ z, q ≠ 0
∴ \(\sqrt{5}\) = \(\frac{p}{q}\) – 3 = rational – rational rational number
∴ \(\sqrt{5}\) is a rational number which is a contradiction.
∴ our assumption is wrong
∴ 3 + \(\sqrt{5}\) is irratjona1.
Question 27.
In a class of 150 students, It was found that 95 like burgers and 79 like pizzas. Assuming every student like at least one of the above, find the number of students who like both burgers and pizzas.
Answer:
n(B∪P) = n(B) + n(P) – n(B ∩ P)
150 = 95 + 79 – n(B ∩ P)
∴ n(B ∩ P) – 95 + 79 – 150 = 24
n(B ∩ P) = 24
Question 28.
If 451/x = 31/y = 51/z, prove that x = 2y + z.
Answer:
Let 451/x = 31/y = 51/z = k
(45)1/x = k ⇒ 45 = kx
31/y = k ⇒ 3 = ky
51/z = k ⇒ 5 = kz
Consider kx = 45 = 9 × 5 = 32 × 5 = (ky)2 kz = k2y kz = k2y-z
∴ x = 2y + z
Question 29.
If x = log2a a, y = log3a 2a, z = log4a 3a. Show that xyz + 1 = 2yz.
Answer:
xyz +1 = log2a a. log3a 2a. log4a 3a + 1
= log3a a. log4a 3a. +1 (∵ logb a. logc b = logc a)
= log4a a +1
= log4aa + log4a 4a (∵ loga a = 1)
= log4a 4a2
= log4a (23)2
= 2 log4a 2a (∵ log an = m log a)
= 2log3a 2a. log4a 3a = 2 yz = RHS
Question 30.
The sum of three numbers in APis -18 and sum of their squares is 140. Find the numbers.
Answer:
(a – d) + a + (a + d) = -18
3a = -18 ⇒ a = -6
(a – d) + a2 + (a + d)2 = 140
![]()
3a2 + 2d2 = 140
3(-6)2 + 2d2 = 140
108 + 2d2 = 140
2d2 = 140- 108
2d2 = 32
d2 = 16
d = 4
∴ The numbers are
-6 – 4, -6, -6 + 4
-10, -6, -2
![]()
Question 31.
Find an integral root between -3 and 3 by inspersion and then using synthetic division solve the equation x3 + 2x2 – 11x -12 = 0.
Answer:
Put x = – 1
(-1)3 + 2(- 1)2 – 11 (- 1) – 12
-1 + 2 + 11 – 12 = 13 – 13 = 0
x = -1 is a root, x + 1 is a factor
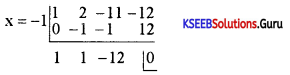
Quotient = x2 + x – 12
Remainder = 0
x3 + 2x2 – 11x – 12 = 0
(x + 1)(x2 + x – 12) = 0
x + 1 = 0, x2 + x – 12 = 0
x = 3, -4 x = -1
The roots are -1. 3, -4
Question 32.
Pradeep invested equal amounts one at 6% SI and the other at 5% CI. If the former earns Rs.437.5 more as interest at the end of two years, find the total amount invested.
Answer:
Let the amount invested = x
P = x r = 6% T = 2years
SI = \(\frac{P \times T \times R}{100}=\frac{x \times 2 \times 6}{100}=\frac{12 x}{100}\) = 0.12x
P = x r = 5% = 0.05 n = 2
A =P(1 + r)n = x(1 + 0.05)2 = x(1.05)2 = 1.1025x
CI = A – P = 1.1025 x – x = 0.1025 x
Given 0.12x – 0.1025x = 437.5
0.0175x = 437.5
Amount invested at 6% SI = 25,000
Amount invested at 5% Cl = 25,000
∴ Total amount invested = 25,000 + 25,000
= Rs. 50,000
Question 33.
A school runs in the morning and afternoon shifts and employs 40 teachers. The average salary of 25 teachers working in the morning shift is Rs.2800/- and the average salary of teachers working the afternoon shift is Rs.3000/- find
(i) the average salary of the teachers in the school.
(ii) the average salary is 5 teachers shifted from morning to afternoon shift,
Answer:
(i) N1 = 25 X1 = 2800
N2 = 15 X2 = 3000
X̄ = \(\frac{\mathrm{X}_{1} \mathrm{~N}_{1}+\mathrm{X}_{2} \mathrm{~N}_{2}}{\mathrm{~N}_{1}+\mathrm{N}_{2}}=\frac{2800(25)+3000(15)}{25+15}=\frac{70000+45000}{40}\) = Rs. 2875
(ii) X1 = 2800 N1 = 20
X2 = 3000 N2 = 20
X̄ = \(\frac{X_{1} N_{1}+X_{2} N_{2}}{N_{1}+N_{2}}\)
= \(\frac{2800(20)+3000(20)}{20+20}=\frac{56000+60000}{40}\) = Rs. 2900
Question 34.
A wholesale dealer sold a machine to a shopkeeper at 20% profit. The shopkeeper sold it to a customer so as to get 25% profit for himself. The difference between the selling price of the shopkeeper and that of the wholesale dealer was found to be Rs.129. Find the initial price of the machine.
Answer:
Let x be C.P. of the machine
SP of wholesale dealer = x + 20% of x = \(\frac{120 x}{100}\)
SP of the shopkeeper = 25% of \(\frac{120 x}{100}+\frac{120 x}{100}\)
\(\frac{120 x}{100}+\frac{25}{100}\left(\frac{120 x}{100}\right)-\frac{120 x}{100}\) = 129
\(\frac{25}{100} \times \frac{120 x}{100}\) = 129
30x = 129 × 100
x = \(\frac{12900}{30}\) = Rs. 430
Question 35.
Find the orthocentre of the triangle formed by the vertices A (5, -2), B (-1, 2) C (1, 4).
Answer:
Let AD, BE be the altitudes.
Now slope of BC =\(\frac{4-2}{1+1}\) = 1
∴ Slope of AD = -1 since AD perpendicular to BC.
∴ Equation to the altitude AD is y + 2 = -1 (x – 5)
or x + y – 3 = 0
Again slope of AC = \(\frac{4+2}{1-5}=-\frac{3}{2}\)
∴ Slope of altitudes BE = \(-\frac{1}{3}=\frac{2}{3}\)
∴ Equation to the altitude BE is
y – 2 = \(\frac{2}{3}\)(x+ 1)
or 2x – 3y + 8 = 0 (2)
Solving (1)and (2), we get x = \(\frac{1}{5}\), y = \(\frac{14}{5}\)
∴ The orthocentre is \(\left(\frac{1}{5}, \frac{14}{5}\right)\).
![]()
Question 36.
Prove that tan 120° +3 sin2 3000_ 2 cosec2 240° – \(\frac{3}{4}\) cot2 60° = \(\frac{10}{3}\)
Answer:
tan 120 = tan(180 – 60) = -tan60° = \(\sqrt{3}\)
sin 300 = sin (360 – 60) = -sin 60 = \(-\frac{\sqrt{3}}{2}\)
cosec 240 = cosec (180 + 60) = —-cosec 60 = \(-\frac{2}{\sqrt{3}}\)
cot 60 = \(\frac{1}{\sqrt{3}}\)
LHS = \(\frac{4}{3}(-\sqrt{3})^{2}+3\left(-\frac{\sqrt{3}}{2}\right)^{2}-2\left(\frac{-2}{\sqrt{3}}\right)^{2}-\frac{3}{4}\left(\frac{1}{\sqrt{3}}\right)^{2}\)
= \(\frac{4}{3}(3)+3\left(\frac{3}{4}\right)-2\left(\frac{4}{3}\right)-\frac{3}{4}\left(\frac{1}{3}\right)\) = 4 + \(\frac{9}{4}-\frac{8}{3}-\frac{1}{4}=\frac{48+27-32-3}{12}=\frac{40}{12}=\frac{10}{3}\) = RHS
Question 37.
Find a point that is equidistant from the points (1, 2), (5, -6), and (3, -4).
Answer:
P = (x, y) A(1, 2) B(5, -6)
PA = PB = PC
PA = PB
\(\sqrt{(x-1)^{2}+(y-2)^{2}}=\sqrt{(x-5)^{2}+(y+6)^{2}}\)
(x – 1)2 + (y – 2)2 = (x – 5)2 + (y + 6)2
![]()
-2x + 10x – 4y – 12y + 5 – 61 = 0, 8x – 16y -56 = 0
x – 2y -7 = 0 (1)
PB = PC
\(\sqrt{(x-5)^{2}+(y+6)^{2}}=\sqrt{(x-3)^{2}+(y+4)^{2}}\)
(x – 5)2 + (y + 6)2 = (x – 3)2 + (y +4)2
![]()
-10x + 6x + 12y – 8y + 61 – 25 = 0
-4x + 4y + 36 = 0
x – y – 9 = 0 (2)
÷ -4

y = 2
x – y – 9 = 0
x – 2 – 9 = 0
x – 11 = 0
x = 11
Required Point = P = (11, 2)
Which is nothing but the circumcenter of the ∆le ABC.
Question 38.
Find the lengths of the altitudes of the triangle whose vertices are (5, 2) (3, -3) and (-4, 3).
Answer:
A = (5,2) B = (3, -3) C = (-4, 3)
Area of ∆ABC = \(\frac{1}{2}\) [x1(y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
= \(\frac{1}{2}\)[5 (-3 – 3) + 3 (3 – 2) -4 (2 + 3)] = \(\frac{1}{2}\)[5 (-6) + 3 (1) – 4 (5)]
= \(\frac{1}{2}\) [-30 + 3 – 20] =\(\frac{1}{2}\)[-47] = \(\left|\frac{-47}{2}\right|=\frac{47}{2}\) = Square units
Area of the ∆ABC = \(\frac{1}{2}\) × BC × AD
AD = \(\frac{2 \Delta \mathrm{ABC}}{\mathrm{BC}}\)
BC = \(\sqrt{(-4-3)^{2}+(3+3)^{2}}=\sqrt{49+36}=\sqrt{85}\)
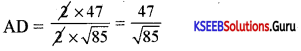
AC = \(\sqrt{(-4-5)^{2}+(3-2)^{2}}=\sqrt{81+1}=\sqrt{82}\)
∆ABC = \(\frac{1}{2}\) × AC ×BE
BE = \(\frac{2 \times \Delta \mathrm{ABC}}{\mathrm{AC}}=\frac{2 \times 47}{2 \times \sqrt{82}}\)
BE = \(\frac{47}{\sqrt{82}}\)
AB = \(\sqrt{(3-5)^{2}+(-3-2)^{2}}=\sqrt{4+25}=\sqrt{29}\)
∆ABC = \(\frac{1}{2}\) × AB ×CF
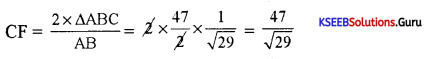
PART – D
IV. Answer any six questions. (6 × 5 = 30)
Question 39.
If x5/3 – y1/3 – z = 0, then show that (x5 – y – z3)3 = 27 x5 yz3
Answer:
x5/3 – y1/3 – z = 0 ⇒ x5/3 – y1/3 = z
Cubing on both sides
(x5/3 – y1/3) = z3
(x5/3)3 – (y1/3)3 – 3x5/3y1/3(x5/3 – y1/3) = z3
x5 – y – 3x5/3 y1/3(z) = z3 ⇒ x5 – y – z3 = 3x5/3 y1/3 z
Cubing on both sides
(x5 – y – z3)3 = 27x5yz3
Question 40.
Using log tables find the value of \(\frac{\sqrt{14.5} \times \sqrt[3]{8.571}}{(16.751)^{2 / 3}}\)
Answer:
logx = log \(\frac{\sqrt{14.5} \times \sqrt[3]{8.571}}{(16.751)^{2 / 3}}\)
= log\(\sqrt{14.5}\) + log\(\sqrt[3]{8.571}\) – log(16.751)2/3
= \(\frac{1}{2}\)log14.54 + \(\frac{1}{3}\)log8.571 – \(\frac{2}{3}\)log(l6.751) .
= \(\frac{1}{2}\)(l.l614) + \(\frac{1}{3}\)(0.9331) – \(\frac{2}{3}\)(1.2240)
= 0.5807 + 0.3110 – 0.816 = 0.0757
x = antilog 0.0757= 1.191
Question 41.
Find the sum of all integers between 60 and 400, which are divisible by 13.
Answer:
Sn = 65 + 78 + 91 +…………..+ 390
a = 5 d = 13 n = ? Tn = 390
Tn = a + (n – 1)d
390 = 65 + (n – 1)13
390 = 65 + 13n- 13
13n = 338 n = 26
Sn = \(\frac{n}{2}\) [a + l] = \(\frac{26}{2}\)(65 +390) = 13 (455) = 5,915
∴ S = 5,915
Question 42.
Two brothers have their annual income in the ratio 8: 5, while their annual expenditures are in the ratio 5 : 3, if they save ₹ 1200/- and ₹ 1000/- per annum. Find their incomes.
Answer:
Let the income be x and expenditure be y.
So the income of two brothers would be 8x and 5x and expenditure would be 5y and 3y.
We knew that Income – Expenditure = Saving
∴ we get:
8x – 5y = 1200 …………..(1)
5x – 3y = 1000 …………..(2)
Solving (1) and (2), we get: x = 1400 and y – 2000
∴ Annual incomes of two brothers are 8x and 5x
= 8 × 1400 & 5 × 1400 = ₹ 11200 and ₹ 7000.
![]()
Question 43.
If the interest on 800 is more than the interest on ₹ 400 by Rs 40 in 2 years. Find the rate of interest.
Answer:
P = 800, T = 2, R = R
SI = \(\frac{800 \times 2 \times R}{100}\)
I1 = 16R
P = 400, T = 2 R = R
SI = \(\frac{400 \times 2 \times \mathrm{R}}{100}\)
I2 = 8R
I1 = I2 = 40
16R – 8R = 40
R = \(\frac{40}{8}\) = 5%
Question 44.
If the cost function C (x) of producing ‘x’ unit of a product is given by C(x) = 500x2 + 2500x + 5000 and if each unit of the product is sold at ₹ 6000. then find BEP.
Answer:
Given C(x) = 500 x2 + 2500x + 5000 (x = output)
Total Revenue = R(x) = Selling price X quantity = 6000 x
For BEP : C (x) = R (x)
500x2 + 250Qx + 5000 = 6000x
500x2 + 2500x – 6000x + 5000 = 0
500x2 – 3500x – 5000x = 0
÷ 500
x2 – 7x + 10 = 0
(x – 5) (x – 2) = 0
x = 5 or 2 units
Question 45.
\(\frac{\mathrm{x} \cdot{cosec}^{2} 30^{\circ} \cdot \sec ^{2} 45^{\circ}}{8 \cos 45^{\circ} \cdot \sin 60^{\circ}}\) = tan2 60° – tan2 30°
Answer:

Question 46.
Find the ratio in which the co-ordinate axes, divide the line joining the points (2, 5) and (1, 9). Find also the coordinates of the points of division.
Answer:
The co-ordinate of the point dividing the join of A (2, 5) and B (1, 9) in the ratio
K: 1 are \(\left(\frac{K+2}{K+1}, \frac{9 K+5}{K+1}\right)\) (1)
(i) If the point lies on x axis then its y co-ordinate is zero
i.e. \(\frac{9 \mathrm{~K}+5}{\mathrm{~K}=1}\) = 0
⇒ K = \(\frac{-5}{9}\)
∴ x axis divides AB externally in the ratio 5 : 9
Substituting K = \(\frac{-5}{9}\) in (1) the co-ordinates of the point of division is \(\left(\frac{K+2}{K+1}, \frac{9 K+5}{K+1}\right)=\left(\frac{\frac{-5}{9}+2}{\frac{-5}{9}+1}, 0\right)=\left(\frac{13}{4}, 0\right)\)
(ii) If the point lies on y axis then its abscissa (x coordinate) = 0
i.e \(\frac{\mathrm{K}+2}{\mathrm{~K}+1}\) = 0
⇒ K = -2
∴ y axis divides AB externally in the ratio 2 : 1
Coordinates of the point of division
= \(\left(\frac{K+2}{K+1}, \frac{9 K+5}{K+1}\right)=\left(0, \frac{9(-2)+5}{-2+1}\right)\) = (0, 13)
![]()
Question 47.
Find the ratio in which the line joining (1, 2) and (4, 3) is divided by the line joining the points (2, 3) and (4, 1)
Answer:
Let A = (2, 3) and B (4, 1). The equation of the line AB is given by
\(\frac{y-3}{x-2}=\frac{1-3}{4-2}\) ⇒ y – 3 = x + 2 ⇒ x + y = 5
Let the line joining the pins C (1, 2) and D (4, 3) cut the line AB at P (x, y) in the ratio r : 1. Then
P = \(\left(\frac{4 r+1}{r+1}, \frac{3 r+2}{r+1}\right)\)
This lies on the line x + y = 5
Thus the co-ordinates of P must satisfy this equation.
∴ \(\frac{4 r+1}{r+1}+\frac{3 r+2}{r+1}\) = 5
4r + 1 + 3r + 2 = 5 (r + 1)
7r + 3 = 5r + 5 ⇒ r = 1
Thus the required ratio is 1 : 1
Question 48.
Show that the following points are the vertices of a rectangle. (1, 6), (-1, -2), (4,1) (-4, 3)
Answer:
Let A = (1, 6), B = (-1, -2), C = (4, 1), D = (-4, 3)
AB = \(\sqrt{(1+1)^{2}+(6+2)^{2}}=\sqrt{4+64}=\sqrt{68}\)
BC = \(\sqrt{(-1-4)^{2}+(-2-1)^{2}}=\sqrt{25+9}=\sqrt{34}\)
CD = \(\sqrt{(4+4)^{2}+(1-3)^{2}}=\sqrt{64+4}=\sqrt{68}\)
DA = \(\sqrt{(1+4)^{2}+(6-3)^{2}}=\sqrt{25+9}=\sqrt{34}\)
∴ AB = CD and BC = AD
i.e., opposite sides are equal.
Further
AC = \(\sqrt{(1+4)^{2}+(6-1)^{2}}=\sqrt{9+25}=\sqrt{34}\)
BD = \(\sqrt{(-1+4)^{2}+(-2-3)^{2}}=\sqrt{9+25}=\sqrt{34}\)
∴ The diagonals AC and BD are equal.
∴ ABCD is a parallelogram with diagonals equal.
∴ ABCD is a rectangle.
PART-E
V. Answer any one equestion. (1 × 10 = 10)
Question 49.
(a) Derive the equation of the straight line is the form \(\frac{x}{a}+\frac{y}{b}\) = 1
Answer:
Let a line cut the x-axis at A and the y-axis at B. Let OA = a and OB = b. Then the length OA = a is called the x-intercept of the line and the length OB = b is called the y-intercept of the line. If ‘ the line passes the origin. Then both the x-intercept and y-intercepts are zero.
Consider the XOY plane. Let the line cut the x-axis at A and the y-axis at B. By data OA = a and OB = b. Thus A = (0, 0) and B = (0, b). Hence the required line is the line joining A and B, Its equation can be obtained by using a two-point form of the equation of a line.
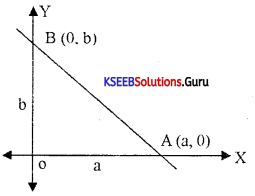
Then the equation of AB is
\(\frac{y-0}{x-a}=\frac{0-b}{a-0}\)
⇒ \(\frac{y}{x-a}=\frac{-b}{a}\) ⇒ ay = -bx + ab ⇒ bx + ay = ab
Dividing throughout by ‘ab’ we have
\(\frac{b x}{a b}+\frac{a y}{a b}=\frac{a b}{a b}\)
This form of equation of the line is called Intercept form.
⇒ \(\frac{x}{a}+\frac{y}{b}\) = 1
(b) The angles of a triangle are in A.P. and the ratio of a number of degrees in the least to the number of radians in the greatest is 60: π. Find the angles of the triangle in radians.
Answer:
A – D, A, A + D
A – D + A + A + D= 180
3A = 180
A = 60°
A- D, A, A+ D Angles in degrees
(A – D)\(\frac{\pi}{180}\), A, \(\frac{\pi}{180}\)(A+D)\(\frac{\pi}{180}\) Angles in radians
Given
\(\frac{A-D}{(A+1) \frac{\pi}{180}}=\frac{60}{\pi}\)

(A – D) 180 = 60(A + D)
(A – D)3 = A + D
3A – 3D = A + D
3A – A = 3D + D
2A = 4D
2(60) = 4D
4D = 120
D = 30°
Angles in degrees are
60 – 30, 60, 60 + 30
A – D, A, A + D
300, 60°, 90°
or Angles in radians are
\(\frac{\pi}{6}, \frac{\pi}{3}, \frac{\pi}{2}\)
(c) Find the number of digits in 2S0. (log 2 = 0,3010)
Answer:
Let x = 250 log x = log 250 = 50 log 2 = 50 × 0.3010 = 15.05
As the characteristic of log x is 15, no. of digits are 15 + 1 = 16.
![]()
Question 50.
(a) Shanmukh buys every year Bank’s cash certificate of value exceeding the last year’s purchase by Rs. 500. After 15 years, he finds that the total value of the certificates purchased by him is Rs.82,500. Find the value of the certificates purchased by him
(a) in the first year and b in the 10lh year.
Answer:
d = Rs.500 n=15 Sn = 82,500 a = ? T10 = ?
Sn = \(\frac{\mathrm{n}}{2}\)[2a + (n – 1)d]
82500 = \(\frac{15}{2}\) [2a+ 14(500)]
\(\frac{82500 \times 2}{15}\) = 2a + 7000
11000 = 2a + 7000
2a = 11000 – 7000 = 4,000
a = 2,000
a = Rs. 2,000
T10 = a + (10 – 1) d = 2000 + 9 (500) = 2000 + 4500 = 6500
T10 = 6,500
(b) x + 3y ≥ 3,2x + y ≥ 2, x ≥ 0, y ≥ 0
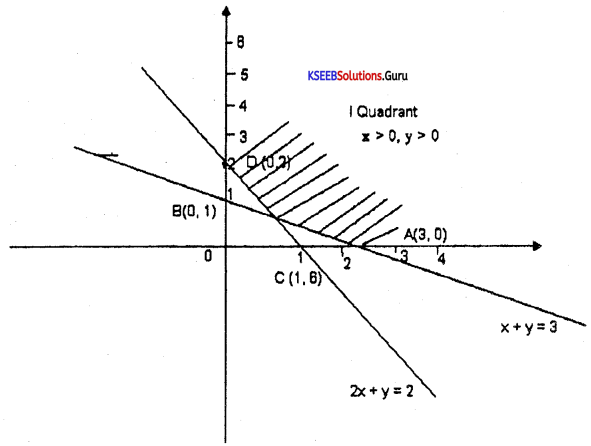
(c) Find the numbers which when divided by 36,40 and 48 leaves same remainder 5.
Answer:
Let us find out the LCM of 36, 40, 48
36 = 22 × 32
40 = 23 × 5
48 = 24 × 3
LCM = 24 × 32 × 51 .
= 16 × 45 = 720
Since 5 has to be the remainder, we have to add 5 to 720
i.e. 720 + 5 = 725