1st PUC Basic Maths Model Question Paper 4 with Answers

Students can Download 1st PUC Basic Maths Model Question Paper 4 with Answers, Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.

Karnataka 1st PUC Basic Maths Model Question Paper 4 with Answers

Time: 3.15 Hours
Max. Marks: 100

Instructions:

1. The questions paper consists of five parts A, B, C, D, and E.
2. Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
3. Write the question numbers properly as indicated in the questions paper

PART-A

I. Answer any ten questions (10 × 1 = 10)

Question 1.
Write the imaginary part of 2 + 3i.
Answer:
3

Question 2.
If A = {a, b, c}, B = {c, d, e, f}. Find A – B.
Answer:
A – B = {a, b}

Question 3.
f: R → R is defined by f(x) = 4x + 3 find f(3/4)
Answer:
f(3/4) = 4(3/4) + 3 = 3 + 3 = 6.

Question 4.
Simplify \(\left(\frac{16}{81}\right)^{-1 / 4}\)
Answer:

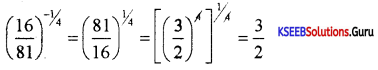
Question 5.
Evaluate x if logx 256 = 4
Answer:
x⁴ = 256
x⁴ = 44 ⇒ x = 4

Question 6.
Find the 10th term of the AP 1, 3, 5
Answer:
a = 1, d = 2, n = 10
Tn = o + (n – 1)d = 1 + (10 – 1)2 = 1 + 9(2) = 1 + 18 = 19

Question 7.
Solve for x.
Answer:
2(x- 3) = 9 + 3(x- 9).

Question 8.
Convert 0.12 into a percentage
Answer:
0.12 = 0.12 × 100%= \(\frac{12}{100}\) × 100% = 12%

Question 9.
Convert – 150° into radians.
Answer:
-150°= -150 × \(\frac{\pi}{180}=\frac{-5 \pi^{c}}{6}\)

Question 10.
Find the slope of a line parallel to the line 3.x + 5y -9 = 0 -3
Answer:
\(\frac{-3}{5}\)

Question 11.
If sin A = \(\frac{3}{5}\) and 90 < A < 180 find cos A
Answer:

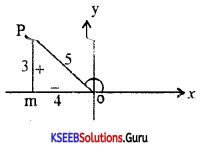
Cos A = -4/5

Question 12.
Define perpetuity?
Answer:
If the annuity payments are made for an infinite period then it is called a perpetuity.

PART-B

II. Answer any Ten questions. (10 × 2 = 20)

Question 13.
Find the number which when divided by 16, 20 and 40 leaves the same remainder 4.
Answer:
16 = 2⁴, 20 = 2² × 5¹, 40 = 2³ × 5¹
LCM = 2⁴ × 5¹ = 16 × 5 = 80
∴ Required number 80 + 4 = 84.

Question 14.
IfA = {2, 3, 4) write all the proper subsets of A.
Answer:
Proper subsets ofA arc {2), {3}, (4), (2, 3), (2, 4), {3, 4}

Question 15.
Find the number of positive divisors and the sum of all positive divisors of 360.
Answer:
360 = 2³ × 3² × 5¹

n = P₁^α₁ × P₂^α₂ × P₃^α₃
P₁ = 2, α₁ = 3, P₂ = 3, α₂ = 2, P₃ = 5, α₃ = 1
T(n) = (1 + α₁)(1 + α₂)(1 + α₃)
T(360) = (3 + 1)(1 + 2)(1 + 1) = (4)(3)(2)=24
S(n) = \(\frac{P_{1}^{\alpha_{1}+1}-1}{P_{1}-1} \times \frac{P_{2}^{\alpha_{2}+1}-1}{P_{2}-1} \ldots \ldots \times \frac{P_{n}^{\alpha_{n}+1}-1}{P_{n}-1}\)
S(360) = \(\frac{2^{4}-1}{2-1} \times \frac{3^{3}-1}{3-1} \times \frac{5^{2}-1}{5-1}=\frac{15}{1} \times \frac{26}{2} \times \frac{24}{1}\) = 1170

Question 16.
Simplify 2(3-2) + \(\left(\frac{1}{3}\right)^{-3}\) + 32
Answer:
\(\frac{2}{3^{2}}\) + 32 + 32
= \(\frac{2+243+81}{9}=\frac{326}{9}\)

Question 17.
Solve for X: logx + log (x – 4) – log (x – 6) = 0
Answer:
logx + log(x – 4) – log(x – 6)= 0
logx(x – 4) – log(x – 6) = 0
log \(\frac{x^{2}-4 x}{x-6}\) = 0
(∵ log 1 = 0) ∴ \(\frac{x^{2}-4 x}{x-6}\) = 1
⇒ x² – 4x = x – 6
x² – 4x – x + 6 = 0
x² – 5x + 6 = 0
x² – 2x – 3x + 6 = 0
x (x – 2) -3 (x – 2) = 0
(x – 2) (x – 2) = 0
x = 2 or x = 3

Question 18.
If the second term of an A.P is 4 and 10th term is 20. Find the 15th term.
Answer:
T₂ – 4 T₁₀ = 20 T₁₅ = ?
T_n = a + (n – 1)d
T₂ = 4
a + (2 – 1) d = 4
a + d = 4 …………..(1)
T₁₀ = 20
a+ (10 – 1)d = 20
a + 9d = 20………..(2)
(2)-(1) gives
a + 9d = 20

∴ d = 2
a + d = 4
a + 2 = 4
a = 4 – 2 = 2
a = 2
T₁₅ = a + (15 – 1)d = a + 14d – 2 + 14(2) = 2 + 28 = 30
T₁₅ = 30

Question 19.
Divide ₹ 1600 between x, y, z so that y may have ₹ 100 morethan.x and z ₹ 200 more then y.
Answer:
Let x’s share be ₹ a.
∴ y’s share is ₹ 100 + a
& z’s share is ₹ 200 + 100 + a .
Given a + 100 + a + 200 + 100 + a = 1600
3a + 400= 1600 3a = 1200 ⇒ a = 40
∴ x, y & z’s share are ₹ 400, ₹500 and ₹700 respectively.

Question 20.
Calculate the simple on ₹ 4,000 at 4% from June 27 to Aug 29 in the same year.
Answer:
P = Rs. 4000R = 4%
June 27th to Aug 29
June : 3 days, July : 31 days, Aug : 29 days
Total = 63 days
T = \(\frac{63}{365}\) =0.1726
SI = \(\frac{4000 \times 0.1726 \times 4}{100}\) = Rs. 27.616

Question 21.
The average age of 10 students ¡n 14 years among them the average age of 4 students is 12 years. Find the average age of the remaining students.
Answer:
Given x̄₁ = i2yr. n₁ = 4
x̄₂ = 1 n=6
And Average of 10 students is 14 years.
∴ 14 = \(\frac{\bar{x}_{1} \mathrm{n}_{1}+\bar{x}_{2} \mathrm{n}_{2}}{\mathrm{n}_{1}+\mathrm{n}_{2}}\)
14 = \(\frac{(12 \times 4)+\left(\bar{x}_{2} \times 6\right)}{4+6}\)
14 = \(\frac{48+6 \bar{x}_{2}}{10}\)
∴ 48 + 6x̄₂ =140
6x̄₂ = 140 – 48
6x̄₂ = 92
∴ x̄₂ = \(\) =15.33yrs.

Question 22.
The sales of a company was 35,000 in June and 30,000 in July. Find the percentage decrease.
Answer:
% decrease = \(\frac{\text { Decrease }}{\text { Initial Value }}\) × 100
Decree = 35, 000 – 30,000 = 5000
% decrease = \(\frac{\text { Decrease }}{\text { Initial Value }}\) × 100
= \(\frac{5000}{35000}\) × 100 = 14.285 ≈ 14.29%

Question 23.
Prove that \(\frac{1-\cos \theta}{\sin \theta}=\frac{\sin \theta}{1+\cos \theta}\)
Answer:
L.H.S = \(\frac{1-\cos \theta}{\sin \theta}=\frac{1-\cos \theta}{\sin \theta} \times \frac{1+\cos \theta}{1+\cos \theta}\)
= \(\frac{1 \cos ^{2} \theta}{\sin \theta(1+\cos \theta)}=\frac{\sin ^{2} \theta}{\sin \theta(1+\cos \theta)}=\frac{\sin \theta}{1+\cos \theta}\) = R.H.S

Question 24.
Find the value of \(\left(\frac{16 \pi}{3}\right)\)
Answer:
tan\(\left(\frac{16 \pi}{3}\right)\) = tan\(\left(4 \pi+\frac{4 \pi}{3}\right)\) = tan\(\frac{4 \pi}{3}\) = tan\(\left(\pi+\frac{\pi}{3}\right)\) = tan\(\frac{\pi}{3}\) = \(\sqrt{3}\)

Question 25.
Find the value of x so that the slope of the line joining the points A(2, 5) and B(x, 13) is 20.
Answer:
Let A =(2,5) B = (x, 13)
Slope m = 20
⇒ \(\frac{13-5}{x-2}\) = 20
⇒ 8 = 20 (x – 2)
⇒ 8 = 20x – 40
⇒ 48 = 20x
∴ x = \(\frac{48}{20}=\frac{12}{5}\)

PART – C

III. Answer any ten questions. (10 × 3 = 30)

Question 26.
In a college \(\left(\frac{2}{5}\right)^{\text {th }}\) of the students play Basket ball and \(\left(\frac{3}{4}\right)^{t h}\) play volley ball. If 50 students play none of these two games and 125 play both, to find the number of students in the college.
Answer:
Let the number of students in the college = x
No of students who play Basket ball = \(\frac{2}{5}\)x
No of students who play Valley ball = \(\frac{3}{4}\)x
No of students who play both = 125
50 students play none of the games.
x-50 = \(\frac{2}{5}\)x + \(\frac{3}{4}\) x – 125
x – \(\frac{2}{5}\) x + \(\frac{3}{4}\) x = -125 + 50
\(\frac{20 x-8 x-15 x}{20}\) = -75
\(\frac{-3 x}{20}\) = -75
x = \(\frac{20 \times 75}{3}\) = 20 × 25 = 500
∴ Total number of students in the college = 500

Question 27.
Prove that 2 + \(\sqrt{3}\) is an irrational number.
Answer:
Sol. If possible let 2 + \(\sqrt{3}\) is a rational number
∴ 2 + \(\sqrt{3}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\), p,q∈z, q ≠ 0
⇒ \(\sqrt{3}=\frac{\mathrm{p}}{\mathrm{q}}\) – 2 = rational – rational = rational number
But \(\sqrt{3}\) is an irrational number

A rational number cannot be equal to an irrational number.
∴ Our assumption is wrong
∴ 2+ \(\sqrt{3}\) is irrational.

Question 28.
Evaluate 3 +5 + 7 + ….+ 61.
Answer:
Here, a=3, d = 5 – 3 = 2, l = Tn = 61
Consider, Tn = a + (n – 1)d
61 = 3 + (n – 1)2
61 – 3 = 2n – 2
58 = 2n – 2
2n = 58 + 2
2n = 60
n = \(\frac{60}{2}\) = 30 Sn = \(\frac{\mathrm{n}}{2}\)(a +1)
Now, S = \(\frac{30}{2}\)(3+61)
= 15 (64)
= 960

Question 30.
A father is 28 years older than the son, after 5 years the father’s age will be 7 years more than twice that of the son. Find their present ages.
Answer:
Let father’s age be x years and son’s age be y years.
Given: x – y = 28 ……………..(1)
After five years father’s age is x + 5 and son’s age is y + 5.
Also given: x + 5 = 2(y + 5) + 7
x + 5 = 2y + 10 + 7
Solving(1) and (2), we get: x = 44 and y = 16
Thus father’s age is 44 years and the son’s age is 16 years.

Question 31.
Three equal principals amount to 3720 after 3, 4 and 5 years at simple interest 6% p.a Find the principal.
Answer:
Amount after 3 years,
P = x, T = 3, R = 6
I₁ = \(\frac{x \times 3 \times 6}{100}\)
A₁ = P+ I = x + 0.18x = 1.18x

Amount after 4 years,
P = x, T = 4, R = 6
I₂ = \(\frac{x \times 4 \times 6}{100}\) = 0.24x
A₂ = x + 0.3x = 1.3x

Amount after 5 years,
P = x, T = 4, R = 6
I₃ = \(\frac{x \times 5 \times 6}{100}\)
A₃ = x + 0.3x = 1.3x
Given A₁ + A₂ + A₃ = 3720
1.18x + 1.24x +1.3x = 3720
3.72x = 3720
x = \(\frac{3720}{3.72}\) = 1000

Each Principle = ₹ 1000
Total Principle = ₹ 3000

Question 32.
The difference between simple interest and Compound interest on a certain sum of money invested for 3 years at 6% p.a is 110.16 Find the sum.
Answer:
Let the sum = x
Simple Interest = \(\frac{x \times 3 \times 6}{100}\) = 0.18 x
Compound interest
A = P(1 + i)ⁿ
= x (1 + 0.06)³
= 1.191016x
CI = A – P
= 0.191016 x- x
= 1.191016 x
Given, Cl -SI =110.16
0.191016x – 0.18x = 110.16
x = \(\frac{110.16}{0.011016}\)
= 10,000 Rs

Question 33.
Find the present value of an annuity of ₹ 3000 for 12 years at 6% p.a. computed half yearly.
Answer:
effective rate of interest
r = \(\left(1+\frac{i}{q}\right)^{q}\) – 1
= \(\left(1+\frac{06}{2}\right)^{2}\) – 1 = 1.0609 – 1 = 0.0609
A = 3000 i = 0.0609 n = 12
P = \(\frac{a\left[(1+i)^{n}-1\right]}{i \times(1+i)^{n}}\)
= \(\frac{3000\left[(1+0.0609)^{12}-1\right]}{0.0609(1+0.0609)^{12}}\)
= \(\frac{3000(2.0328-1)}{0609 \times 2.0328}\) = 25027.96₹
(by direct calculation (without rounding in between values) with calculator, answer is 25027.89)

Question 34.
A Dental Clinic purchased a certain number of chairs at an average price of ₹ 190 each. The average price of 30 chairs was ₹ 175 and that of the remaining chairs was ₹ 200/-. Find the total number of chairs the clinic purchased.
Answer:
Assumed that the number of chair the clinic purchased = x.
Total average price = ₹ 190
Average Price No. of chair
x̄₁ = ₹ 175 N₁ = 10
x̄₂ = ₹ 200 N₂ = (x – 10)
Combined average price = \(\frac{\bar{x}_{1} N_{1}+\bar{x}_{2} \mathrm{~N}_{2}}{(10)+(x-10)}\)
190 = \(\frac{(175 \times 10)+(200 \times(x-10))}{x}\)
190 = \(\frac{1750+200 x-2000}{x}\)
∴ 190x = 200x – 250
250 = 200x- 190x
250= 10x
∴ x = \(\frac{250}{10}\) = ₹ 25
Total Number of chairs purchased by the clinic = 25

Question 35.
Savithri sold her bag at a loss of 7%. Had she been able to sell it at a gain of 9% it would have fetched 64 more than it did. What was the cost price of the bag?
Answer:
Let C.P. = 100
Loss at 7% ⇒ SP = 93
Gain of 9% ⇒ SP = 109
Diff = 109 – 93 = 16

Then cost price of the bag is = \(\frac{100 \times 64}{16}\) = ₹ 400

Question 36.
P.T. (1 + tan A – sec A) (1 + cot A + cosec A) = 2
Answer:
LHS = (1 + tan A – sec A) (1 + cot A + cosec A)
= 1 + cotA + cosecA + tanA + tanA × cotA + tanA × cosec A-sec A-sec A. cotA – secA . cosec A

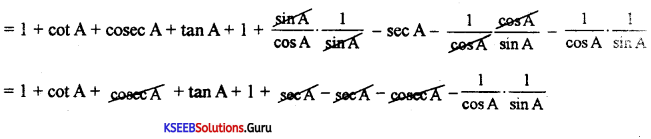
= 2 + \(\left[\cot \mathrm{A}+{Tan} \mathrm{A}-\frac{1}{\cos \mathrm{A} \cdot \sin \mathrm{A}}\right]\) = 2 + \(\left[\frac{\cos A}{\sin A}+\frac{\sin A}{\cos A}-\frac{1}{\cos A \sin A}\right]\)
= 2 + \(\left[\frac{\cos ^{2} A+\sin ^{2} A-1}{\cos A \sin A}\right]\) = 2 + \(\left[\frac{1-1}{\cos A \sin A}\right]\) = 2 + \(\frac{0}{\cos A \sin A}\)
= 2 + 0 = 2

Question 37.
Find x if
\(\frac{x \sin ^{2} 300^{\circ} \cdot \sec ^{2} 240}{\cos ^{2} 225 \cdot {cosec}^{2} 240}\) = cot2 315° . tan2 300°
Answer:
sin 300 = sin (360 – 60) = -sin 60 = \(\frac{\sqrt{3}}{2}\)
sec 240 = sec (180 + 60) = -sec 60 = -2
cos225 = cos(180 + 45)= -cos45 = –\(\frac{1}{\sqrt{2}}\)
cosec 240 = cosec (180 + 60) = -cosec 60 = –\(\frac{2}{\sqrt{3}}\)
cot 315 = cot(360 – 45) – cot45 = – 1
Tan 300 = Tan(360 – 60) = -Tan60 = –\(\sqrt{3}\)

Substituting these values the given equation becomes
\(\frac{x\left(-\frac{\sqrt{3}}{2}\right)^{2}(-2)^{2}}{\left(\frac{-1}{\sqrt{2}}\right)^{2}\left(\frac{-2}{\sqrt{3}}\right)^{2}}\) = (-1)2 \((-\sqrt{3})^{2}\)
\(\frac{x \cdot \frac{3}{4} \cdot 4}{\frac{1}{2} \cdot \frac{4}{3}}\) = (1) (3)
\(\frac{12 \mathrm{x}}{\frac{4}{4}{6}}\) = 3 ⇒ \(\frac{12 x}{4} \times \frac{6}{4}\) = 3
\(\frac{72 \mathrm{x}}{16}\) = 3 ⇒ \(\frac{48}{12}=\frac{2}{3}\)
∴ x = \(\frac{2}{3}\)

Question 38.
Find the coordinates of the circumcentre of the triangle so formed by the points (1, 1) (2, -1) and (3, 2)
Answer:
Let A = (1, 1), B(2, -1) C(3, 2)
Let S(x, y) be the circumcentre of the triangle ABC.
Then SA = SB = SC.
⇒ SA² = SB² = SC²

Consider SA² = SB²
i.e.(x – 1)² + (y – 1)² = (x – 2)² + (y + 1)²
i.e. x² – 2x + 1 + y² – 2y + 1 = x² – 4x + 4 + y² + 2y + 1
⇒ 2x – 4y = 3 (1)

Again consider SA² = SC²
(x – 1)² + (y – 1)² = (x – 2)² + (y + 1)²
x² – 2x + 1 + y² – 2y + 1 = x² – 6x + 9 + y² – 4y + 4
⇒ 4x + 2y = 11 (2)
Solving (1) and (2) we get x = 5/2 and y = 1/2
Thus the circumcentre is given by \(\left(\frac{5}{2}, \frac{1}{2}\right)\)

PART-D

IV. Answer any six questions. 6 × 5 = 30

Question 39.
A relation R on a collection of a set of integers defined by R = {(x,y): x – y is a multiple of 3}. Show that R is an equivalence relation on Z.
Answer:
0 = x – x is a multiple of 3 ∴ x R x ∴ R is reflexive
Let x Ry ⇒ x-y is a multiple of 3 ⇒ x -y = 3k, k ∈ Z y – x = – (x – y)= -3k = 3(-k) is a multiple of 3 -k∈Z
∴ y R x ∴ R is symmetric Let x R y & y R z
∴ x-y is a multiple of 3 ∴ x-y = 3a, a ∈ Z
∴ y-z is a multiple of 3 ∴ y-z = 3b, b ∈ Z
(x-y) + (y-z) = 3a + 3b = 3(a + b)
∴ x-z = 3(a + b),a + b ∈ Z
∴ x – z is a multiple of 3 ∴ x R z ∴ R is transitive
∴ R is an equivalence relation on Z.

Question 40.
Find the sum of all numbers between 50 an 200 which are divisible by 11.
Answer:
AP is given by
55, 66, 77,… 198
Here a = 55, l = T_n =198, d = 11
Now, T_n = a + (n – 1) d
198 = 55 + (n- 1)11
198 – 55 = (n – 1) 11
\(\frac{143}{11}\) = n – 1
n – 1 = 13
n = 13 + 1
n = 14
Now consider:
S_n = \(\frac{\mathrm{n}}{2}\)(a + l)
S₁₄ = \(\frac{14}{2}\)(55 + 198)
= 7 (253)
= 1,771

Question 41.
The income of three persons Anil, Akbar, and Antony is 6: 5: 4, and their expenditures are in the ratio of 3: 2: 1. If Anil saves ₹ 120 out of his income of ₹ 1500. Find the saving of Akbar and Antony.
Answer:
Let the income be x and the expenditure be y.
Incomes are 6x, 5x and 4x and their expenditures are 3y, 2y and y.
Given : Anil’s income = ₹ 1500/-
⇒ 6x = 1500 ⇒ x = 250
Anil’s expenditure = 3y = Income – Savings
3y = 1500 – 120
3y = 1380 y = ₹ 460
Thus Akbar’s incoe = 5x = 5 × 250 = ₹1250
Akbar’s expenditure = 2y = 2 × 460 = ₹920
Antony’s income = 4x = 4 × 250 = ₹1000
Antony’s expenditure = y = ₹1000

Question 42.
A sum of money lent at compound interest for 2 years at 20% p.a. would fetch Rs.482 more, if the interest was payable half yearly than if it was payable annually. Find the sum.
Answer:
A₁ = Amount wjjen the interest payable is annually
A₂ = Amount when the interest payable is half yearly
A₂ – A₁ = 482
Let the princible be P n = 2 years r = 20%
A₁ =P(1 +0.20)²
A₁ = P(1.2)² = 1.44 P
Half yearly R = 20% q = 2
r = \(\left(1+\frac{\mathrm{R}}{\mathrm{q}}\right)^{q}\) – 1
= \(\left(1+\frac{0.20}{2}\right)^{2}\) – 1 = 1.21 – 1 = 0.21 = 2.1%
A₂ = P(1 + 0.21)²
A₂ = P(1.21)² = 1.4641 P
A₂ – A₁ = Rs.482
1.4641 P- 1.44 P = 482
0.0241 P = 482
P = \(\frac{482}{0.0241}\) = Rs. 20,000

Question 43.
A person purchases a house for Rs.25 lakhs with Rs. 5 lakhs as a down payment. The rest of the amount he loans from a bank that offers 16% p.a compound interest and has to repay the loan in 20 equal annual installments. If the first installment is paid at the end of the third year, find how much he has to pay each year?
Answer:
P = 25,00,000 – 5,00,000 = 20,00,000
r = 16% = 0.16 d = 2 n = 20 A=?
A = \(\frac{\mathrm{P} \cdot \mathrm{r} \cdot(1+\mathrm{r})^{\mathrm{n}+\mathrm{d}}}{(1+\mathrm{r})^{\mathrm{n}}-1}=\frac{20,00,000(0.16)(1+0.16)^{22}}{(1+0.16)^{20}-1}=\frac{83,79,647}{18.46}\) = 4,53,935.37

Question 44.
Find the equation of the locus of a point that moves so that its distance from (3, 2) is equal to its distance from 2x + y = 3
Answer:
A = (3,2)
Let P (x, y) be any point on the locus
PA = distance of P from the line 2x + y – 3 = 0
\(\sqrt{(x-3)^{2}+(y-2)^{2}}=\left|\frac{2 x+y-3}{\sqrt{2^{2}+1^{2}}}\right|\)
(x – 3)² + (y – 2)² = \(\left(\frac{2 x+y-3}{\sqrt{5}}\right)^{2}\)
x² – 6x + 9 + y² – 4y + 4 = (4x² + y² + 9 + 4xy – 6y – 12x)/5
5x² – 30x + 45 + 5y² – 20y + 20 = 4x² + y² + 9 + 4xy – 6y – 12x
x² – 4xy + 4y² – 18x – 14y + 56 = 0

Question 45.
Evaluate using log tables \(\)
Answer:
Let x = \(\)
Log x = log\(\) = log \(\) + log 0.5789 – log(13.46)3/2
= log (6.43)1/2 + log0.5789-log (13.46)3/2 = \(\frac{1}{2}\)log(6.43) + log0.5789- \(\frac{3}{2}\) log(13.46)
= 0.4041 + 1̄.7626- 1.6935 = -1.5268 = -1 – 0.5268 = -1 -1 + 1 – 0.5268
= -2 + 0.4732 = 2̄ .4732
x̄ = Antilog (2̄ .4732) = 0.0297

Question 46.
Find the equation of a straight line passing through the point (3, 4) such that the sum of its intercepts on the axes is 14.
Answer:
Let the x and y intercepts of the line be a and b respectively so that a + b = 14 or b = 14 – a
Thus the equation of the line in die intercept form is
\(\frac{x}{a}+\frac{y}{14-a}\) = 1
But it passes through the point (3, 4).
therefore \(\frac{3}{a}+\frac{4}{14-a}\) = 1 a 14-a
3 (14 – a) + 4a = a(14 – a)
i.e., a² – 13a + 42 = 0
i.e., (a – 6) (a – 7) = 0 or a = 6 or a = 7
If a = 6 then b = 8; If a = 7 then b = 7
Therefore equations of the hoes are \(\frac{x}{6}+\frac{y}{8}\) = 1 or \(\frac{x}{7}+\frac{y}{7}\) = 1

Question 47.
Find the coordinates of the reflection of the point (1, 2) about the line 3x + 4y – 1 = 0. Sol. Let P (1, 2) be the given point and 3x + 4y – 1 = 0 be the given line. Draw PM perpendicular to the given line and produce it to P’ such that PM = MP’. Then M is the foot and P’ is the reflection of the point P. Also M is the mid-point of PP’ and PP’ is perpendicular to the given line.
Answer:
Let P’ = (a, b). We first find the coordinates of the foot M.
Now any line perpendicular to 3x + 4y – 1 = 0 is 4x – 3y + k = 0.
But this perpendicular line passes through P (1,2)
∴ 4(1) – 3(2) + k = 0
∴ Equation to the perpendicular line PP’ is 4x – 3y + 2 = 0
Now M is the point of intersection of the given line and the above.
Hence solving these two equations we get x = –\(\frac{1}{5}\), y = \(\frac{2}{5}\)

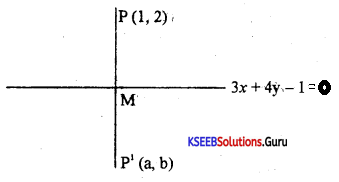
∴ The foot M is \(\left(-\frac{1}{5}, \frac{2}{5}\right)\).
But M = Mid-point of PF = \(\left(\frac{a+1}{2}, \frac{b+2}{2,}\right)\).
Therefore
\(\frac{a+1}{2}=-\frac{1}{5}, \frac{b+2}{2}=\frac{2}{5}\)
a = –\(\frac{7}{5}\); b = – \(\frac{6}{5}\)
Required reflection of P is P’ = \(\left(-\frac{7}{5},-\frac{6}{5}\right) \)

Question 48.
If sec a = \(\frac{13}{5}\) where 270° < a < 360° find the value of \(\frac{2 \sin \alpha-3 \cos \alpha}{4 \sin \alpha+9 \cos \alpha}\)
Answer:
α lies in 4th Quadrant .
cos α and sec α are positive and rest arernegative
sin α = \(\frac{-12}{13}\)
cos α = \(\frac{5}{13}\)
Given Expression

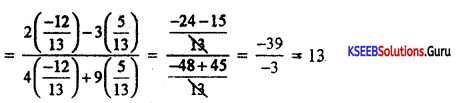
PART-E

V. Answer any one equestion. (1 × 10 = 10)

Question 49.
(a) Find the equation of the straigh&fine passing through the point of intersection x² + 2y + 3 = 0 and 3x + 4y + 7 = 0 and has a slope \(\)
Answer:
x + 2y+ 3 = 0 x 2
3x + 4y + 7 = 0 x 1

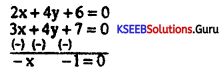
x = -1
x + 2y + 3 = 0
-1 + 2y + 3 = 0
2y + 2 = 0
y = -1
(x1, y1) = (-1,-1) = m= \(\frac{-3}{2}\)

(b) P.T \(\frac{\tan \mathbf{A}}{1-\cot \mathrm{A}}+\frac{\cot \mathbf{A}}{1-\tan \mathrm{A}}\) =1+SecA.CosecA
Answer:
LHS = \(\frac{\frac{\sin A}{\cos A}}{1-\frac{\cos A}{\sin A}}+\frac{\frac{\cos A}{\sin A}}{1-\frac{\sin A}{\cos A}}\)

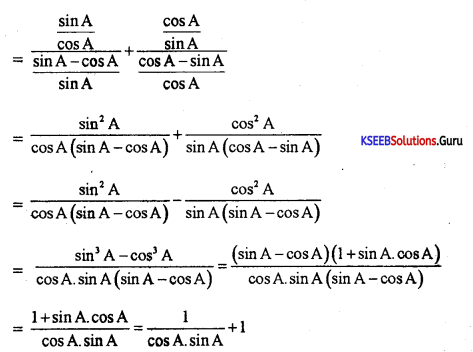
= sec A. cosec A + 1 = RHS

(c) If log 5 = 0.6990, find the number of digits in the integral part of 5²³
Answer:
Consider log (5²³) =23 log 5
=23 (06990) = 16.077
Since the characteristic of log (5²³) is 16, there are 17 digits in an integral part of 5²³

Question 50.
(a) Find the sum to n terms of the GP 0.6 + 0.66 + 0.666 +……….
Answer:
Let S_n = 0.6 + 0.66 + 0.666 +……. to n terms
= 6[0.1 + 0.11 + 0.111 + ……… to n terms]
= \(\frac{6}{9}\)[0.9 + 0.99 + 0.999 +……… to n terms]
= \(=\frac{6}{9}\left[\left(1-\frac{1}{10}\right)+\left(1-\frac{1}{100}\right)+\left(1-\frac{1}{1000}\right)+\ldots \text { to } \mathrm{n} \text { terms }\right]\)

= \(\frac{6}{9}\)[(1 + 1 + 1 + ……… to n terms) – \(\left(\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+\ldots \text { to n terms }\right)\)]

= \(\frac{6}{9}\left[n-\frac{\frac{1}{10}\left(1-\frac{1}{10^{n}}\right)}{1-\frac{1}{10}}\right]\)
= \(\frac{6}{9}\left[\mathrm{n}-\frac{1}{10} \times \frac{10}{9}\left(1-\frac{1}{10^{n}}\right)\right]\)
S_n = \(\frac{6}{9}\left[\mathrm{n}-\frac{1}{9}\left(1-\frac{1}{10^{\mathrm{n}}}\right)\right]=\frac{2}{3}\left[\mathrm{n}-\frac{1}{9}\left(1-\frac{1}{10^{\mathrm{n}}}\right)\right]\)

(b) A batsman’s average score for a number of intlings was 21.75 runs per innings. In the next three inning he scored 28,34 and 37 runs. And his average for all the inning was revised by 1.125 runs. How many inning did he play?
Answer:
Let the number of innings he played = x
∴ Total runs in ’x’ innings = 21.75 x
Again total runs in next 3 innings = 28 + 34 + 37 = 99 runs.
Number of inning raised to = (x + 3)
New Average after 3 inning raised to = 21.75 + 1.125 = 22.875

∴ Average run after (x + 3) innings = \(\frac{\text { Total runs of all the innings }}{\text { Total no. of innings }}\)
22.875 = \(\frac{21.75 x+99}{x+3}\)
∴ (22875) (x+ 3) = 21.75x+ 99
22.87x + 68.625 = 21.75x + 99
(22.875x – 21.75x) = 99 – 68.625
1.125x = 30.375
∴ x = \(\frac{30.375}{1.125}\) = 27
∴ Total innings played = x + 3 = 27 + 3 = 30

(c) A confectioner makes and sells Chocolates. He sells one box of Chocolates at The cost of manufacturing is Rs.60/box as variable cost and Rs.2000 as Fixed C* (i) Revenue function (ii) the cost function.
Answer:
Let x be the number of boxes of chocolates
Total cost = variable cost + fixed cost = 60x + 2000
Revenue function = 180x