KSEEB SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Ex 8.3 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Exercise 8.3.
Karnataka SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Exercise 8.3
Question 1.
Prove that \(\sqrt{5}\) is irrational.
Solution:
Let us assume, to the contrary, that \(\sqrt{5}\) is rational.
∴ \(\sqrt{5}=\frac{a}{b}\)
∴ b × \(\sqrt{5}\) = a
By Squaring on both sides,
5b2 = a2 …………. (i)
∴ 5 divides a2.
5 divides a.
∴ We can write a = 5c.
Substituting the value of ‘a’ in eqn. (i),
5b2 = (5c)2 = 25c2
b2 = 5c2
It means 5 divides b2.
∴ 5 divides b.
∴ ‘a’ and ‘b’ have at least 5 as a common factor.
But this contradicts the fact that a’ and ‘b’ are prime numbers.
∴ \(\sqrt{5}\) is an irrational number.
Question 2.
Prove that \(3+2 \sqrt{5}\) is irrational.
Solution:
Let us assume that \(3+2 \sqrt{5}\) is an irrational number.
Here, p, q, ∈ z, q ≠ 0
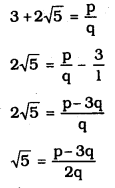
\(\sqrt{5}\) is rational number.
∵ \(\frac{p-3 q}{2 q}\) is rational number.
But \(\sqrt{5}\) is not a rational number.
This contradicts the fact that,
∴ \(3+2 \sqrt{5}\) is an irrational number.
Question 3.
Prove that the following are irrationals :
i) \(\frac{1}{\sqrt{2}}\)
ii) \(7 \sqrt{5}\)
iii) \(6+\sqrt{2}\)
Solution:
i) Let \(\frac{1}{\sqrt{2}}\) is a rational number.
\(\frac{1}{\sqrt{2}}=\frac{\mathrm{p}}{\mathrm{q}}\)
\(\sqrt{2}=\frac{q}{p}\)
By Squaring on both sides,
2 × p2 = q2
2, divides q2.
∴ 2, divides q
∵ q is an even number.
Similarly ‘p’ is an even number.
∴ p and q are even numbers.
∴ Common factor of p and q is 2.
This contradicts the fact that p and q also irrational.
∴ \(\sqrt{2}\) is an irrational number.
∴ \(\frac{1}{\sqrt{2}}\) is an irrational number.
ii) Let \(7 \sqrt{5}\)is a rational number.
∴ \(7 \sqrt{5}=\frac{p}{q}\)
\(\sqrt{5}=\frac{p}{7 q}\)
Here,\(\frac{p}{7 q}\) is one rational number.
It means \(\sqrt{5}\) which is equal also a rational number.
This contradicts to the fact that \(\sqrt{5}\) is an irrational number.
This contradicts to the fact that \(7 \sqrt{5}\) is rational number.
∴ \(7 \sqrt{5}\) is a rational number.
iii) Let \(6+\sqrt{2}\) is a rational number.
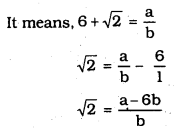
\(\frac{a-6 b}{b}\) is a rational number, b
∴ \(\sqrt{2}\) is also rational number.
This contradicts to the fact that \(\sqrt{2}\) is an irrational number.
This contradicts to the fact that \(6+\sqrt{2}\) is a rational number.
∴ \(6+\sqrt{2}\) is an irrational number.
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Ex 8.3 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 8 Real Numbers Exercise 8.3, drop a comment below and we will get back to you at the earliest.