KSEEB SSLC Class 10 Maths Solutions Chapter 2 Triangles Ex 2.4 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 2 Triangles Exercise 2.4.
Karnataka SSLC Class 10 Maths Solutions Chapter 2 Triangles Exercise 2.4
Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm2 and 121 cm2, If EF = 15.4 cm., find BC.
Solution:
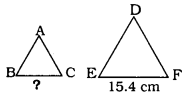
If ∆ABC ~ ∆DEF, then
\(\frac { { ar }(\Delta { ABC }) }{ { ar }(\Delta { DEF }) } =\frac { { BC }^{ 2 } }{ { EF }^{ 2 } } \)
\(\frac{64}{121}=\frac{\mathrm{BC}^{2}}{(15.4)^{2}}\)
\(\mathrm{BC}^{2}=\frac{64}{121}=\frac{\mathrm{BC}^{2}}{(15.4)^{2}}\)
\(\mathrm{BC}^{2}=\frac{64}{121} \times \frac{237.16}{1}\)
∴ BC = 8 × 1.4
∴ BC = 11.2 cm
Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
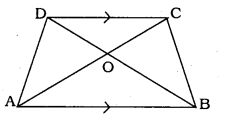
Solution:
Data: Diagonals of a trapezium ABCD with AB||DC intersect each other at the point O. We have AB = 2 CD.
To prove: \(\frac { { Ar }(\Delta { A }{ OB }) }{ { Ar }(\Delta { COD }) } =?\)
As per similarity criterion, ∆AOB and ∆COD are,
∆AOB ~ ∆COD
\(\frac { { Ar }(\Delta { AOB }) }{ { Ar }(\Delta { COD }) } =\frac { { AB }^{ 2 } }{ { DC }^{ 2 } } \)
\(=\frac{(2 \mathrm{DC})^{2}}{\mathrm{DC}^{2}}(\cdot \mathrm{AB}=2 \mathrm{DC})\)
\(=\frac{4 \mathrm{DC}^{2}}{1 \mathrm{DC}^{2}}\)
\(\frac { { Ar }(\Delta { AOB }) }{ { Ar }(\Delta { COD }) } =\frac { 4 }{ 1 } \)
= 4 : 1
Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that
\(\frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { DBC }) } =\frac { { AO } }{ { DO } } \)
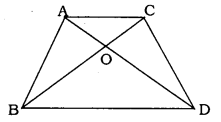
Solution:
Data: ABC and DBC are two triangles on the same base BC. If AD intersects BC at O.
To Prove: \(\frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { DBC }) } =\frac { { AO } }{ { DO } } \)
Construction: Draw AP ⊥ BC and DM ⊥ BC.
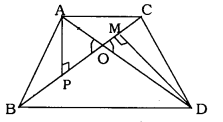
Area of ∆ = \(\frac{1}{2}\) × base × height
\(\frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { DBC }) } =\frac { \frac { 1 }{ 2 } \times BC\times AP }{ \frac { 1 }{ 2 } \times BC\times DM } \)
\(=\frac{\mathrm{AP}}{\mathrm{DM}}\)
In ∆APO and ∆DMO,
∠APO = ∠DMO = 90° (construction)
∠AOP = ∠DOM (Vertically opposite angles)
∴ ∆APO ~ ∆DMO
(∵ Similarity criterion is A.A.A.)
\(\frac{\mathrm{AP}}{\mathrm{DM}}=\frac{\mathrm{AO}}{\mathrm{DO}}\)
\(\Rightarrow \quad \frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { DBC }) } =\frac { { AO } }{ { DO } } \)
Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
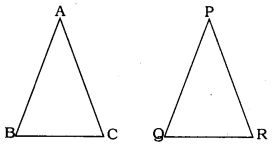
Solution:
In ∆ABC ~ ∆PQR
\(\frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { PQR }) } =\left( \frac { { AB } }{ { PQ } } \right) ^{ 2 }=\left( \frac { { BC } }{ { QR } } \right) ^{ 2 }=\left( \frac { { AC } }{ { PR } } \right) ^{ 2 }\) …………. (1)
Area of ∆ABC = Area of ∆PQR
\(\Rightarrow \quad \frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { PQR }) } =1\) …………. (2)
Substituting the eqn (2) in eqn (1)
\(1=\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{PR}}\right)^{2}\)
⇒ AB = PQ, BC = QR, AC = PR
∴ ∆ABC ≅ ∆PQR (∵ S.S.S postulate)
Question 5.
D, E, and F are respectively mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
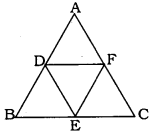
Solution:
Data: D. E and F are respectively midpoints of sides AB, BC and CA of ∆ABC.
To Prove: Ratio of the areas of ∆DEF and ∆ABC.
If a line divides two sides of a triangle in the same ratio, then the line is parallel to the third side and it is half of that side
\(\mathrm{DE} \| \mathrm{AC} \quad \mathrm{DE}=\frac{1}{2} \mathrm{AC}\)
\(\mathrm{EF} \| \mathrm{AB} \quad \mathrm{EF}=\frac{1}{2} \mathrm{AB}\)
\(\mathrm{DF} \| \mathrm{BC} \quad \mathrm{DF}=\frac{1}{2} \mathrm{BC}\)
\(\frac { { Ar }(\Delta { DEF }) }{ { Ar }(\Delta { ABC }) } =\frac { { DF }^{ 2 } }{ { BC }^{ 2 } } \quad ({ Theorem }6)\)
\(\frac { { Ar }(\Delta { DEF }) }{ { Ar }(\Delta { ABC }) } =\frac { \left( \frac { 1 }{ 2 } { BC } \right) ^{ 2 } }{ { BC }^{ 2 } } \)
\(\frac { { Ar }(\Delta { DEF }) }{ { Ar }(\Delta { ABC }) } =\frac { \frac { 1 }{ 4 } { BC }^{ 2 } }{ { BC }^{ 1 } } =\frac { 1 }{ 4 } =1:4\)
Question 6.
Prove that the ratio of the areas , of two similar triangles is equal to the square of the ratio of their corresponding medians.
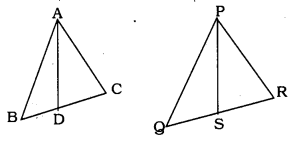
Solution:
Let ∆ABC ~ ∆PQR
AD and PS are mid-point lines of ∆ABC and ∆PQR.
∆ABC ~ ∆PQR
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{PR}}\) ………………… (1)
∠A = ∠P, ∠R = ∠Q, and ∠C = ∠R (2)
AD and PS are mid-point lines
\(B D=D C=\frac{B C}{2}\)
and \(\quad \mathrm{QS}=\mathrm{SR}=\frac{\mathrm{QR}}{2}\)
\(\frac{A B}{P Q}=\frac{B D}{Q S}=\frac{A C}{P R}\) …………… (3)
In ∆ABD and ∆PQS,
∠B = ∠Q ………. Eqn (2)
and \(\frac{A B}{P Q}=\frac{B D}{Q S}\) ………. Eqn (3)
∴ ∆ABD ~ ∆PQS (SAS Postulate)
\(\frac{A B}{P Q}=\frac{B D}{Q S}=\frac{A D}{P S}\) ……………. (4)
\(\frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { PQR }) } =\left( \frac { { AB } }{ { PQ } } \right) ^{ 2 }=\left( \frac { { BC } }{ { QR } } \right) ^{ 2 }=\left( \frac { { AC } }{ { PR } } \right) ^{ 2 }\)
From Eqn. (1) and Eqn. (4), we have
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AD}}{\mathrm{PS}}\)
\(\Rightarrow \quad \frac { { Ar }(\Delta { BC }) }{ { Ar }(\Delta { PQR }) } =\left( \frac { { AD } }{ { PS } } \right) ^{ 2 }\)
Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
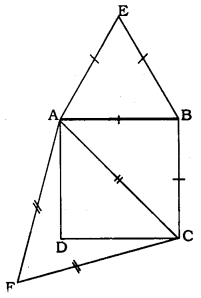
Solution:
Data: Equilateral triangle ABE is on AB of square ABCD. Equilateral triangle ACF is on diagonal AC.
To Prove: \((\Delta A B E)=\frac{1}{2} \text { Ar }(\Delta A C F)\)
\(\frac { { Ar }(\Delta { ABE }) }{ { Ar }(\Delta { ACF }) } =\frac { { AB }^{ 2 } }{ { AC }^{ 2 } } \quad { Theorem }6\)
\(=\frac{A B^{2}}{A B^{2}+B C^{2}}\)
∵ Pythagoras theorem
\(=\frac{\mathrm{AB}^{2}}{2 \mathrm{AB}^{2}}\)
∴ AB = AC sides of square
\(=\frac{1 \times A B^{2}}{2 \times A B^{2}}\)
\(\frac { { Ar }(\Delta { ABE }) }{ { Ar }(\Delta { ACF }) } =\frac { 1 }{ 2 } \)
Tick the correct answer and justify:
Question 8.
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangles ∆ABC and ∆BDE is :
A) 2 : 1
B) 1 : 2
C) 4 : 1
D) 1 : 4
Solution:
C) 4 : 1
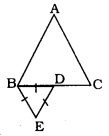
\(\frac { { Ar }(\Delta { ABC }) }{ { Ar }(\Delta { BDE }) } =\frac { { BC }^{ 2 } }{ { BD }^{ 2 } } =\frac { { BC }^{ 2 } }{ \left( \frac { 1 }{ 2 } { BC } \right) ^{ 2 } } \)
\(=\quad \frac{1}{1 / 4}=\frac{4}{1}\)
= 4 : 1
Question 9.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio :
A) 2 : 3
B) 4 : 9
C) 81 : 16
D) 16 : 81
Solution:
D) 16 : 81
∴ (4)2 : (9)2 = 16 : 81.
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 2 Triangles Ex 2.4 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 2 Triangles Exercise 2.4, drop a comment below and we will get back to you at the earliest.