KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.4 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.4.
Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.4
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:
cosec2 A – cot2 A = 1
cosec2 A = 1 + cot2 A
cosec2 A = cot2 A + 1
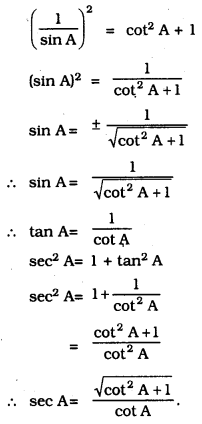
Question 2.
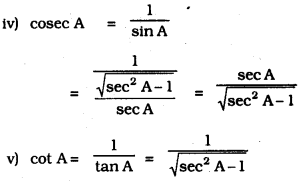
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
i) sin2 A + cos2 A = 1
sin2 A = 1 – cos2 A

Question 3.
Evaluate :
i) \(\frac{\sin ^{2} 63^{\circ}+\sin 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
ii) sin 25° cos 65° + cos 25° sin 65°
Solution:
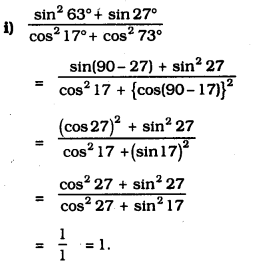
ii) sin 25° cos 65° + cos 25° sin 65°
= sin 25° cos (90° – 25°) + cos 25° sin (90° – 25°)
= sin 25° sin 25° + cos 25° + cos 25°
= sin2 25° + cos2 25°
= 1. [∵ cos2 θ + sin2 θ = 1]
Question 4.
Choose the correct option. Justify your choice.
i) 9 sec2 A – 9 tan2 A.
A) 1
B) 9
C) 8
D) 0
Solution:
B) 9
9 sec2 A – 9 tan2 A
= 9(sec2 A – tan2 A)
= 9 × 1
= 9
ii) (1+tan θ + sec θ) (1+ cot θ- cosec θ) =
A) 0
B) 1
C) 2
D) -1
Solution:
C) 2
(1+tan θ + sec θ) (1+ cot θ- cosec θ)
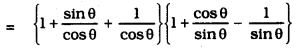
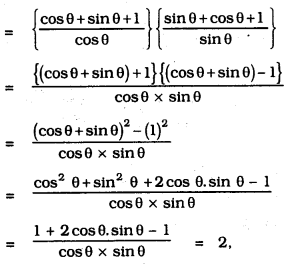
iii) (sec A + tan A) (1 – sin A) =
A) sec A
B) sin A
C) cosec A
D) cos A
Solution:
D) cos A
(sec A + tan A) (1 – sin A)
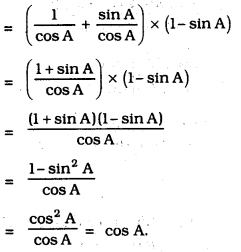
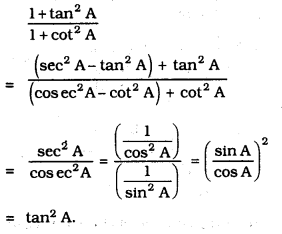
iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\) =
A) sec2 A
B) -1
C) cot2 A
D) tan2 A
Solution:
D) tan2 A
Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
![]()
Solution:
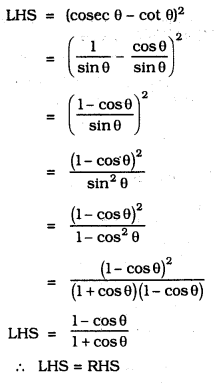
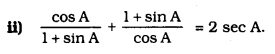
Solution:

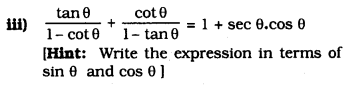
Solution:
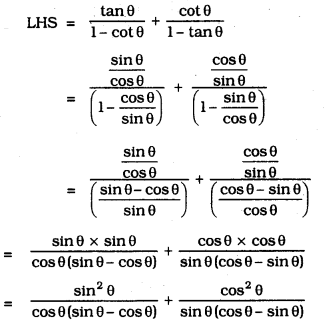

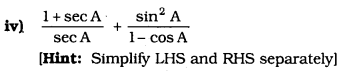
Solution:
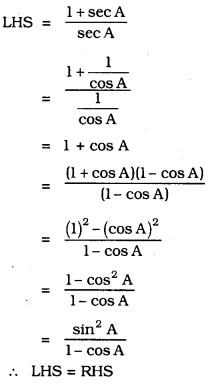
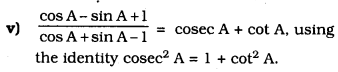
Solution:
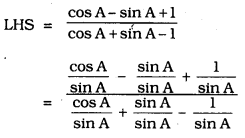

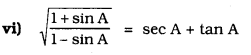
Solution:
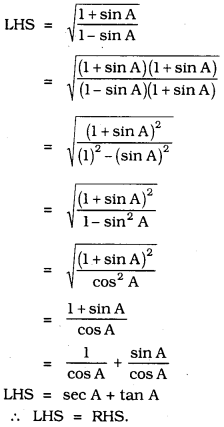
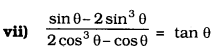
Solution:
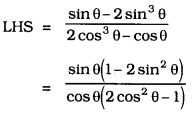
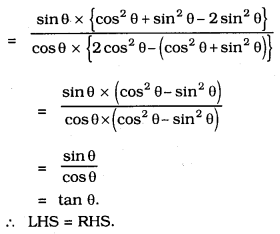
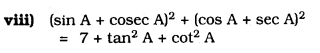
Solution:


Solution:
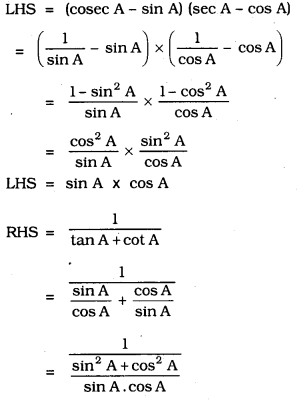
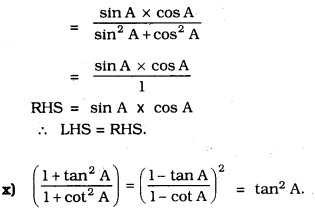
Solution:
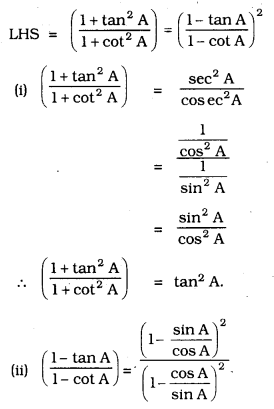

We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Ex 11.4 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 11 Introduction to Trigonometry Exercise 11.4, drop a comment below and we will get back to you at the earliest.