Students can Download Chapter 2 Fractions and Decimals Ex 2.3, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3
Question 1.
Find :
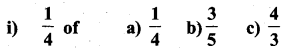
Solution:
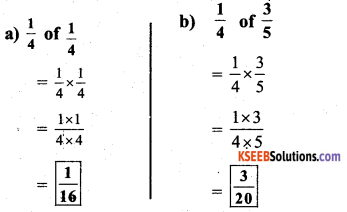
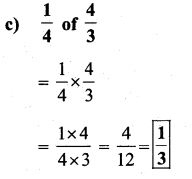
ii)
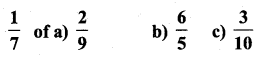

Question 2.
Multiply and reduce to lowest form (if possible)
i)
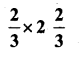
Solution:

![]()
ii)
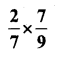
Solution:

iii)
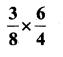
Solution:
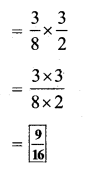
iv)
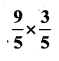
Solution:
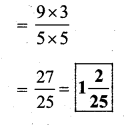
v)
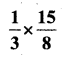
Solution:

vi)
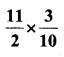
Solution:
![]()
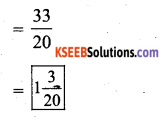
vii)
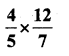
Solution:

Question 3.
Multiply the following fractions:
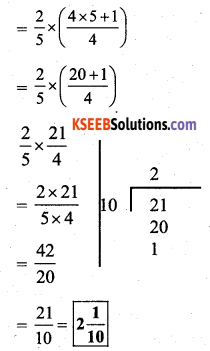
i)
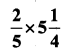
Solution:
![]()
ii)
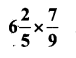
Solution:
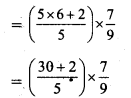
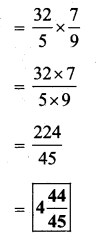
iii)
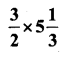
Solution:

![]()
iv)
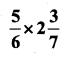
Solution:

v)
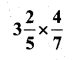
Solution:
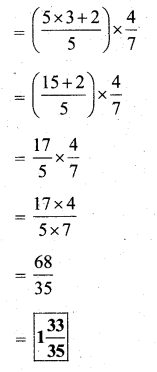
![]()
vi)
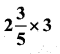
Solution:

vii)
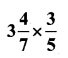
Solution:
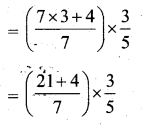

Question 4.
Which is greater :
i)
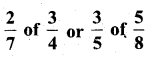
Solution:
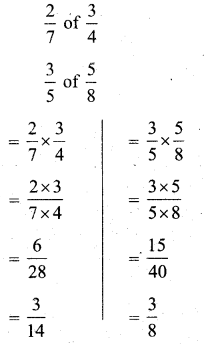
Now,
we have to find greater of
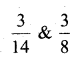
To compare fractions, we make denominator equal.
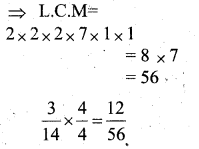
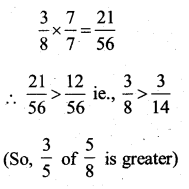
ii)
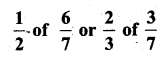
Solution:

Now,
we have to find greater of \(\frac{3}{7}\) & \(\frac{2}{7}\)
Since denominator is same, number with greater numerator is greater.i.e., \(\frac{3}{7}>\frac{2}{7}\)
∴ Thus \(\frac{1}{2}\) of \(\frac{6}{7}\) is greater
![]()
Question 5.
Saili plants 4 saplings in a row, in her garden. The distance between two adjacent saplings is \(\frac{3}{4}\)m. Find the distance between the first and the last sapling.
Solution:
Saili plants 4 saplings, in a row.
The distance between each sapling = \(\frac{3}{4}\) m
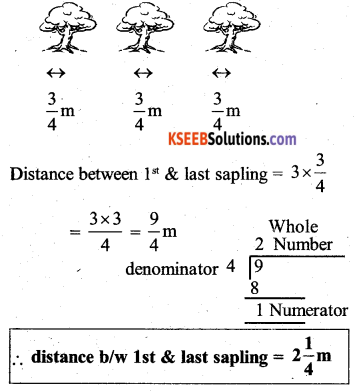
Question 6.
Lipika reads a book for \(1 \frac{3}{4}\) everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book ?
Solution:
Number of hours read everyday = \(1 \frac{3}{4}\) hours
Number of days to read whole book = 6 days
Therefore,
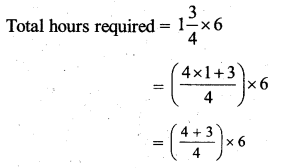

![]()
Question 7.
A car runs 16 km using 1 litre of petrol. How much distance will it cover using \(2 \frac{3}{4}\) litres of petrol.
Solution:
Distance of car runs in 1 litre = 16km

∴ Car will run 44 km in \(2 \frac{3}{4}\) litre of petrol.
Question 8.
a) i) Provide the number in the box □, such that \(\frac{2}{3} \times \square=\frac{10}{30}\)
Solution:

ii) The simplest form of the number obtained in □ is ___
Solution:

b) i) Provide the number in the box □, such that \(\frac{3}{5} \times \square=\frac{24}{75}\)
Solution:
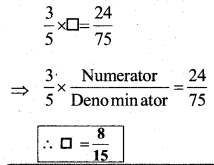

b) ii) The simplest form of the number obtained in □ is ___.
Solution:
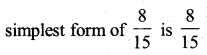
it cannot be simplified further