Students can Download Chapter 12 Algebraic Expressions Ex 12.3, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.3
Question 1.
If m = 2, find the value of:
i) m – 2
2 – 2 = 0
ii) 3m – 5
3 × 2 – 5 = 6 – 5 = 1
iii) 9 – 5m
9 – 5 × 2 ÷ 9 – 10 = -1
![]()
iv) 3m2 – 2m – 7
= 3 × 22 – 2 × 2 – 7
= 3 × 4 – 4 – 7
= 12 – 11 = 1
v)
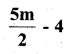
Solution:
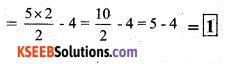
Question 2.
If p = -2, find the value of :
Solution:
i) 4p + 7
= 4x – 2 + 7
= -8 + 7 = -1
ii) -3p2 + 4p + 7
= -3 (-2)2 + 4 (-2) + 7
= 3 × 4 – 8 + 7
= 12 – 8 + 7
= -13
![]()
iii) -2p3 – 3p2 – 4p + 7
= -2 (-2)3 – 3(2)2 + 4 (-2) + 7
= -2(-8) – 3(4) – 8 + 7
= 16 – 12 – 8 + 7
= 16 + 7 – 12 – 8
= 23 – 20 = 3
Question 3.
Find the value of the following expressions, when x = -1:
i) 2x – 7
= 2(-1) – 7
= -2 – 7 = -9
ii) -x + 2
= -1 + 2 = 1
iii) x2 + 2x + 1
= 1 – 2 + 1 = 0
iv) 2x2 – x – 2
= 2(-1)2 – (-1) – 2
= 2 × 1 + 1 – 2
= 2 + 1 – 2 = 1
![]()
Question 4.
If a = 2, b = -2, find the value of:
i) a2 + b2
= 22 + (-2)2
= 4 + 4 = 8
ii) a2 + ab + b2
= 22 + 2 × -2 + (-2)
= 4 – 4 + 4 = 4
iii) a2 – b2
= (2)2 – (-2)2 = 4 – 4 = 0
Question 5.
When a = 0, b = -1, find the value of the given expressions :
i) 2a + 2b
= 2 × 0 + 2 × -1
= o – 2 = -2
ii) 2a2 + 2b2 + 1
= 2(0)2 + (-1)2 + 1
= 0 + 1 + 1 = 2
iii) 2a2b + 2ab2 + ab
= 2 × 02 × -1 + 2 × 0 × (-1)2 + 0 × -1
= 0 + 0 + 0 = 0
iv) a2 + ab + 2
= (0)2 + 0 × -1 + 2
= 0 + 0 + 2 = 2
![]()
Question 6.
Simplify the expressions and find the value if x is equal to 2
Solution:
i) x + 7 + 4 (x – 5)
= x + 7 + 4x – 20 (re-arranging the terms)
= 5x – 13 = 5(2) – 12
= 10 – 13 = -3
ii) 3(x + 2) + 5x – 7
= 3x + 6 + 5x – 1
= 8x – 1 = 8(2) – 1
= 16 – 1 = 15
iii) 6x + 5 + 5(x – 2)
= 6x+ 5x – 10
= 11x – 10 = 11(2) – 10
= 22 – 10 = 12
iv) 4(2x – 1) + 3x + 11
= 8x – 4 + 3x + 11
= 8x + 3x – 4 + 11 (re-arranging the terms)
= 11x + 7 = 11(2) + 7 = 22 + 7 = 29
Question 7.
Simplify these expressions and find their values if x = 3, a = -1, b = -2.
i) 3x – 5 – x + 9
= 3x – x + 9 – 5
= 2x + 4 = 2(3) + 4 = 6 + 4 = 10
ii) 2 – 8x + 4x + 4
= 2 + 4 – 4x
= -4x + 6
= -4 × 3 + 6
= -12 + 6 = -6
![]()
iii) 3a + 5 – 8a + 1
= 3a – 8a + 5 + 1
= -5a + 6
= -5(-1) + 6
= 5 + 6 = 11
iv) 10 – 3b – 4 – 5b
= -3b – 5b + 10 – 4
= -8b + 6
= -8 (-2) + 6
= 16 + 16 = 22
v) 2a – 2b – 4 – 5 + a
= 2a – 2b – 9
= 3a – 2b – 9
= 3(-1) – 2 (-2) – 9
= -3 + 4 – 9
= -12 + 4 = -8
![]()
Question 8.
i) If z = 10, find the value of z3 – 3(z – 10)
= (10)3 – 3 (10 – 10)
= 1000 – 3(0)
= 1000 – 0 = 1000
ii) If p = -10, find the value of p2 – 2p – 100
= (10)2 – 2(-10) – 100
= 100 + 20 – 100
= 120 – 100
= 20
Question 9.
What should be the value of a if the value of 2x2 + x – a equals to 5, when x = 0 ?
Solution:
= 2x2 + x – a
= 2(0)2 + 0 – a
= 5
= 0 + 0 – a = 5
∴ a = -5
![]()
Question 10.
Simplify the expression and find its value when a = 5 and b = -3, 2(a2 + ab) + 3 – ab
= 2a2 + 2ab + 3 – ab
= 2(5)2 + 2 × 5 × -3 + 3 – 5 × -3
= 2 × 25 – 30 + 3 + 15
= 50 – 30 + 3 + 15
= 50 + 3 + 15 – 30
= 68 – 30 = 38