Students can Download Chapter 12 Algebraic Expressions Ex 12.2, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.2
Question 1.
Simplify combining like terms :
i) 21b – 32 + 7b – 20b
(re-arranging the terms)
= 21b + 7b – 20b – 32
= 28b – 20b – 32
= 8b – 32
ii) z2 + 13z2 – 5z + 7Z2 – 15z
(re-arranging the terms)
= -z2 + 13z2 – 5z – 15z + 7z3
= 12z2 – 20z + 7z3
iii) p – (p – q) – q – (q – p)
= p – p + q – q – q + p
(re-arranging the terms)
![]()
= p – q
![]()
iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= 3a – a – a – 2b + b + b – ab – ab + 3ab
![]()
= a + ab
v) 5x2y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
(re-arranging the terms)
= 5x2y + 3yx2 – 5x2 + x2 – 3y2 – y2 – 3y2 + y2
= 8x2y – 4x2 – 7y2 + 8xy2
vi) (3y2 + 5y – 4) – (8y – y2 – 4) .
3y2 + 5y – 4 – 8y – y2 – 4
(re-arranging the terms)
3y2 + y2 + 5y – 8y – 4 + 4
= 14y2 – 3y
Question 2.
Add:
i) 3mn, -5mn, 8mn, -4mn
3mn + 8nm – 5mn – 4mn
(re-arranging the terms)
= 11mn – 9mn = 2mn
ii) t – 8tz, 3tz – z, z – t
![]()
(re-arranging the terms)
= -8tz + 3tz = -5tz
iii) -7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
-7mn + 12 mn + 9mn – 2mn + 5 + 2 – 8 – 3
(re-arranging the terms)
= -7mn – 2mn + 12mn + 9mn + 7 – 11
= -9mn + 21 mn -4
= 12mn – 4
iv) a + b -3, b – a +3, a – b + 3
![]()
(re-arranging the terms)
= (2a – a + 2b – b + 6 – 3)
= a + b + 3
v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(re-arranging the terms)

= 17x + 51
vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(re-arranging the terms)
= 5m – 4m + 2m – 7n + 3n – 3mn + 2 – 5
= 7m – 4m – 7n + 3n – 3mn – 3
= 13m – 4n – 3mn – 3
vii) 4x2y, – 3xy2, 5y2, 5x2y
(Re-arranging the terms)
4x2y + 5x2y – 3xy2 – 5xy2
= 9x2y – 8xy2
viii) 3p2q2 – 4pq + 5, 10p2q2, 15 + 9pq + 7p2q2
3p2q2 – 10p2q2 + 7p2q2 – 4pq + 9pq + 5+ 15
(Re-arranging the terms)
= 3p2q2 + 7p2q2 – 10p2q2 – 4pq + 9pq + 5 + 15
![]()
= 5pq + 20
![]()
ix) ab – 4a, 4b – ab, 4a – 4b
![]()
(Re-arranging the terms)
(All terms are cancelling)
= 0
x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
(Re arranging the terms)
![]()
= -x2 – y2 – 1
Question 3.
Subtract :
i) -5y2 from y2
= y2 – (-5y2)
= y2 + 5y2 = 6y2
ii) 6xy from – 12xy
= -12xy – (6xy)
= -12xy – 6xy = -18xy
iii) (a – b) from (a + b)
= a + b – (a – b)
![]()
= 2b
iv) a(b – 5) from b(5 – a)
= ab – 5a from 5b – ab
= (5b – ab) – (ab – 5a)
= 5b – ab – ab + 5a
= 5a – 5b – 2ab
v) -m2 + 5mn from 4m2 – 3mn + 8
= (4m2 – 3mn + 8) – (-m2 + 5mn)
= 4m2 – 3mn + 8 + m2 – 5mn
= 4m2 + m2 – 3mn – 5mn + 8
= 5m2 – 8mn + 8
vi) -x2 + 10x – 5 from 5x – 10
= (5x – 10) – (-x2 + 10x – 5)
= 5x – 10 + x2 – 10x + 5
= 5x – 10x + x2 – 10 + 5
= x2 – 5x – 5
vii) 5a2 – 7 ab + 5b2 from 3ab – 2a2 – 2b2
= (3ab – 2a2 – 2b2) – (5a2 – 7ab + 5b2)
= 3ab – 2a2 – 2b2 – 5a2 + 7ab – 5b
= -2a2 – 5a2 – 2b2 – 5b2 + 7ab + 3ab
= -7a2 – 7b2 + 10ab
![]()
viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
= (5p2 + 3q2 – pq) – (4pq – 5q2 – 3p2)
= 5p2 + 3q2 – pq2 – 4pq + 5q2 + 3p2
= 5p2 + 3p2 + 3q2 + 5q2 – 4pq – pq
= 8p2 + 8q2 – 5pq
Question 4.
a) What should be added to x2 + xy + y2 to obtain 2x2 + 3xy ?
Solution:
= 2x2 + 3xy – (x2 + xy + y2)
= 2x2 + 3xy – x2 – xy – y2 – 2x2 – x2 + 3xy – xy – y2
(re-arranging the terms)
∴ x2 + 2xy – y2 should be added to x2 + xy + y2 to get 2x2 + 3xy
b) What should be subtracted from 2a + 8b + 10 to get -3a + 7b + 16 ?
Solution:
= (2a + 8b + 10) – (-3a + 7b + 16)
= 2a + 8b+ 10 + 3a – 7b – 16
= 2a + 3a + 8b – 7b + 10 – 16
(re-arranging the terms)
= 5a + b – 6
∴ (5a + b – 6) should be subtracted from 2a + 8b +10 to get -3a + 7b + 16.
Question 5.
What should be taken away from – 4y2 + 5xy + 20 to obtain -x2 – y2 + 6xy + 20?
Solution:
= (3x2 – 4y2 + 5xy + 20) – (-x2 – y2 + 6xy + 20)
= 3x2 – 4y2 + 5xy + 20 + x2 + y2 – 6xy – 20
= 3x2 + x2 – 4y2 + y2 + 5xy – 6xy + 20 – 20
(re – arranging the terms)
= 4x2 – 3y – xy
∴ 4x2 + 3y2 – xy should be taken away from 3x2 – 4y2 + 5xy + 20 to obtain -x2 – y2 + 6xy + 20
Question 6.
From the sum of 3x – y + 11 and -y – 11, subtract 3x – y – 11.
Solution:
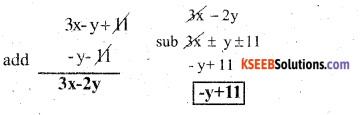
![]()
b) From the sum of 4 + 3x and 5 – 4x + 2x2, subtract the sum of 3x2 – 5x and -x2 + 2x + 5.
Solution:

or
[(4 + 3x) + (5 – 4x + 2x2)] – [(3x2 – 5x) + (x2 + 2x + 5)]
= 4 + 3x + 5 – 4x + 2x2 – 3x2 + 5x + x2 – 2x – 5 = 4 + 3x – 4x + 2x2 + 5 – 3x2 + x2 + 5x – 2x – 5
(re-arranging the terms)
![]()
= 2x + 4