Karnataka Board Class 9 Maths Chapter 13 Surface Area and Volumes Ex 13.5
Question 1.
A matchbox measures 4 cm × 2.5 cm × 1.5 cm. What will be the volume of a packet containing 12 such boxes ?
Solution:
Match box is in the form of cuboid.
Its length, l = 4 cm.
breadth, b = 2.5 cm.
height, h = 1.5 cm.
∴ Volume of Cuboid, V = l × b × h
= 4 × 2.5 × 1.5
V = 15 cm3.
Volume of 1 match box is 15 cm3.
Volume of 12 match boxes …?… .
= 15 × 12
= 180 cm3.
Question 2.
A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold ? (1 m3 = 1000 l)
Solution:
Length of cuboidal water tank, l = 6 m
breadth b = 5 m
height, h =4.5 m
∴ Volume of cuboidal water tank, V= l × b × h
= 6 × 5 × 4.5
V= 135 m3.
1 m3 = 1000 l.
135 m3 = ? = 135 × 1000
= 135000 lit.
∴ Number of litres of water tank = 1350000 litres.
Question 3.
A cuboidal vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid ?
Solution:
Volume of cuboidal vessel, V = 380 m3.
length, l = 10 m
breadth, b = 8 m height, h = ?
Volume of vessel, V= l × b × h
380 = 10 × 8 × h
380 = 80 h
![]()
∴ h = 4.75 m.
Question 4.
Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of Rs. 30 per m3.
Solution:
Length of cuboidal pit, l = 8 m
breadth, b = 6 m height, h = 3 m
∴ Volume of pit, V = l × b × h
= 8 × 6 × 3
= 144 m3.
∴ Cost of digging a cuboidal 1 m3 is Rs. 30
Cost of digging a cuboidal pit for 144 m3 … ? …
= 144 × 30
= Rs. 4320.
Question 5.
The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are respectively 2.5 m and 10 m.
Solution:
Volume of cuboidal tank, V = 50000 lit.
1 c.c = 1000 litres
∴ Volume of tank = \(\frac{50000}{1000}\) = 50 c.c
length of tank, l = 2.5 m
height, h = 10m
breadth,b = ?
Volume of cuboid, V = l × b × h
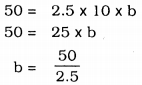
∴ b = 2m.
Question 6.
A village, having a population of 4000, requires 150 litres of water per head per day. It has a tank measuring 20m × 15m × 6m. For how many days will the water of this tank last ?
Solution:
Length of cuboid water tank, l = 20 m
breadth, b = 15 m
height, h = 6 m
Volume, V = ?
Volume of water tank, V = l × b × h
= 20 × 15 × 6
= 1800 m3.
1m3 = 1000 litres
∴ 1800m3 = 1800 x 1000
= 1800000 litres.
Water required daily per man= 150 litres
∴ Quantity of water required for 4000 men?
= 4000 × 150
= 600000 litres.
Quantity of water for 1 day = 600000
Number of days for consuming 1800000 litres … ? …
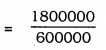
= 3 Days.
Question 7.
A godown measures 40 m × 25 m × 15 m. Find the maximum number of wooden crates each measuring 1.5 m × 1.25 m × 0.5 m that can be stored in the godown
Solution:
Length of rectangular godown, l1 = 40 m
breadth, b1 = 25 m
height, h1 = 10 m
∴ Volume of godown, V= l1 × b1 × h1
= 40 × 25 × 10
= 10000 m3.
Length of wooden crate, l2 = 1.5 m
breadth, b2 = 1.25 m
height, h2 = 0.5 m
∴ Volume of wooden crate. V = l2 × b2 x h2
= 1.5 × 1.25 × 0.5
= 0.9375 m3.
For 0.9375 m3, 1 crate
![]()
= 10666.66
Question 8.
A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Solution:
Each side of a cube, a = 12 cm.
∴ Volume of cube, V = a3
= (12)3
= 1728 cm3.
Solid cube is cut into 8 cubes of equal volume.
Volume of each small cube,
![]()
∴ l3 = 216
∴ l = 6 cm.
∴ Each side of small cube is 6 cm.
Ratio of outer area :
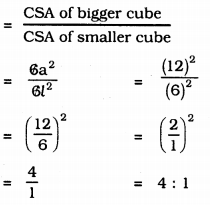
Question 9.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
Solution:
Depth of river, h = 3m
breadth, b = 40 m
1 Km. = 1000 m
∴ 2 Km. = 2000 m.
Speed of the river per hour is 2 Km.
For 60 minutes, 2000m
For 1 minute …?… = \(\frac{2000}{60}\)
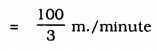
∴ Depth of river in 1 minute, l = \(\frac{100}{3}\) m.
Volume of water flows in 1 minute,
V = l × b × h
= \(\frac{100}{3}\) × 40 × 3
= 4000 m3
∴ In One minute, 4000 m3 water reaches the sea.