Karnataka Board Class 9 Maths Chapter 13 Surface Area and Volumes Ex 13.4
(Assume π = \(\frac{22}{7}\), unless stated otherwise)
Question 1.
Find the surface area of a sphere of radius :
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm.
Solution:
![]()
Surface area of the sphere = \(4 \pi r^{2}\)
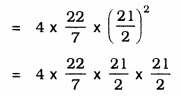
= 22 × 3 × 21
= 1386 cm2.
(ii) r = 5.6 cm. = \(\frac{56}{10}\)cm.
Surface area of the sphere = \(4 \pi r^{2}\)
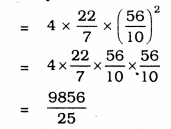
= 394.24 cm2.
(iii) r = 14 cm.
Surface area of the sphere = \(4 \pi r^{2}\)
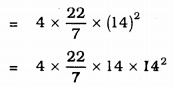
= 88 × 28
= 2464 cm2.
Question 2.
Find the surface area of a sphere of diameter :
(i) 14 cm
(ii) 21 cm
(iii) 3.5 m.
Solution:
(i) Diameter, d = 14 cm.
![]()
Surface area of a sphere = \(4 \pi r^{2}\)
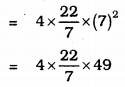
= 616 cm2.
(ii) Diameter, d = 21 cm.
![]()
Surface area of a sphere = \(4 \pi r^{2}\)
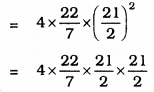
= 1386 cm2.
(iii) Diameter, d = 3.5 m. = \(\frac{7}{2}\)
![]()
Surface area of a sphere = \(4 \pi r^{2}\)
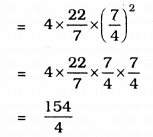
= 38.5 m2.
Question 3.
Find the total surface area of a hemisphere of radius 10 cm.
(Use π = 3.14 )
Solution:
r = 10 cm.
Total surface area of a hemisphere = \(3 \pi r^{2}\)
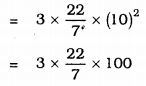
= 942 cm2.
Question 4.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution:
Radius of spherical balloons be r1 and r2, r1 = 7 cm. and r2 = 14 cm.
Ratio of surface area

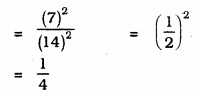
∴ Ratio of surface areas of the balloons = 1 : 4.
Question 5.
A hemispherical bowl made of brass has an inner diameter of 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs. 16 per 100 cm2.
Solution:
Inner diameter of hemispherical bowl = 10.5 cm.
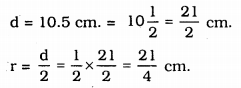
Curved surface area of the bowl = \(2 \pi r^{2}\)
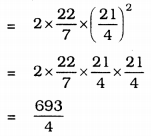
= 173.25 cm2.
Cost of tin-plating for 100 cm2 is Rs. 16.
Cost of tin-plating for 173.25 sq.cm. …?…
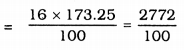
= Rs. 27.72.
Question 6.
Find the radius of a sphere whose surface area is 154 cm2.
Solution:
Total surface area of a sphere= 154 cm2
Radius, r =?
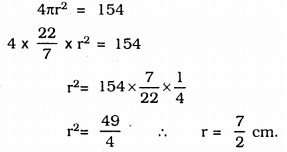
∴ r = 3.5 cm
Question 7.
The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface areas.
Solution:
Let the diameter of earth be d’ unit
∴ Diameter of Moon = \(\frac{d}{4}\)
radius of the earth = \(\frac{\mathrm{d}}{2}\)
radius of the moon = \(\frac{1}{2} \times \frac{\mathrm{d}}{4}=\frac{\mathrm{d}}{8}\)
Ratio of surface area,

= 1 : 16
Question 8.
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Solution:
Thickness of the hemispherical bowl = 0.25 cm.
inner radius, r = 5 cm.
∴ Outer Surfce area= 5 + 0.25 = 5.25 cm.
Outer Curved Surface area = 2πr2
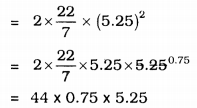
= 173.25 cm2.
Question 9.
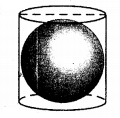
A right circular cylinder just encloses a sphere of radius r (see Fig. 13.22). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder
(iii) ratio of the areas obtained in (i) & (ii).
Solution:
(i) If radius of a sphere is ‘r’ cm, its Surface area = 4πr2
(ii) height of cylinder, h = diameter of sphere
h = r + r
∴ h = 2r
∴ Curved surface area of cylinder = 2πrh
= 2πr × h
= 2πr × 2r
= 4πr2

= 1 : 1