KSEEB Solutions for Class 9 Maths Chapter 12 Circles Ex 12.6

Karnataka Board Class 9 Maths Chapter 12 Circles Ex 12.6

Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.

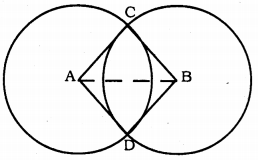
Solution:
Data: Two circles having centres A and B, intersect at C and D.
To Prove: ∠ACB = ∠ADB.
Construction: Join A and B.
Proof: In ∆ABC and ∆ABD,
AC = AD (∵ radii of same circle are equal)
BC = DD
AB is common.
∴ ∆ABC ≅ ∆ABD (SSS Postulate.)
∴ ∠ACB = ∠ADB.

Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm., find the radius of the circle.

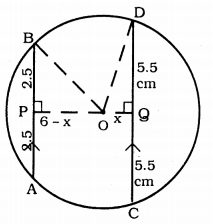
Solution:
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre.
Distance between AB and CD is 6 cm.
To Prove: Radius of the circle, OP =?
Construction: Join OP and OQ, OB, and OD.
Proof: Chord AB || Chord CD.
AB = 5 cm, and CD =11 cm.
OP ⊥ AB
∴ BP = AP = \(\frac{5}{2}\) = 2.5 cm.
OQ⊥CD
∴ CQ = QD = \(\frac{11}{2}\) = 5.5 cm.
PQ = 6 cm. (Data)
Let OQ = 2 cm then, OP = (6 – x) cm.
In ∆BPO, ∠P = 90°
As per Pythagoras theorem,
OB² = BP² + PO²
= (2.5)² + (6 – x)²
= 6.25 + 36 – 12x + x²
OB² = x²– 12x + 42.25 …………….. (i)
In ∆OQD, ∠Q= 90°
∴ OD² = OQ² + QD²
= (x)² + (5.5)²
OD² = x² + 30.25 ……………….. (ii)
OB = OD (∵ radii of same circle)
From (i) and (ii).
x² – 12x + 42.25 = x² + 30.25
-12x = 30.25 – 42.25
-12x = -12
12x = 12
∴ x = \(\frac{12}{12}\)
∴ x = 1 cm.
From (ii),
OD² = x² + 30.25
= (1)² + 30.25
= 1 + 30.25
∴ OD² = 31.25
OD = \(\sqrt{31.25}\)
∴ OD = 5.59 cm.
∴ Radius of circle OP = OD = 5.59 cm.

Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm, from the centre, what is the distance of the other chord from the center?

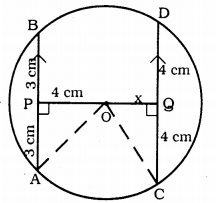
Solution:
Data: Chords of a circle are 6 cm. and 8 cm. are parallel. The smaller chord is at distance of 4 cm. from the centre.
To Prove: Distance between bigger chord and centre =?
Construction: Join OA and OC.
Proof: AB || CD, AB = 6 cm, CD = 8 cm.
OP⊥CD, OQ⊥CD.
In ∆OPA, ∠P = 90°
∴ OA² = OP² + PA² (According to Pythagoras theorem)
= (4)² + (3)² = 16 + 9
OA² = 25
∴ OA = 5 cm.
OA = OC = 5 cm. (radii of the same circle.)
Now, in ∆OQC,
OC² = OQ² + QC²
(5)² = x² + (4)²
25 = x² + 16
x² = 25 – 16 = 9
∴ x = \(\sqrt{9}\) ∴ x = 3 cm.
∴ Bigger chord is at a distance of 3 cm from the centre.

Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.

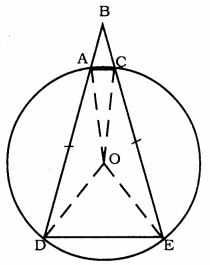
Solution:
Data: The vertex of angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle.
To Prove: ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre. OR
∠ABC= \(\frac{1}{2}\) [∠DOE – ∠AOC].
Construction: OA, OC, OE, OD are joined.
Proof: In ∆AOD and ∆COE,
OA = OC, OD = OE radii of same circle.
AD = CE (Data)
∴ ∆AOD ≅ ∆COE (SSS Postulate)
∠OAD = ∠OCE ……….. (i)
∴∠ODA = ∠OEC …………. (ii)
OA = OD
∴ ∠OAD = ∠ODA …………. (iii)
From (i) and (ii),
∠OAD = ∠OCE = ∠ODA = ∠OEC = x°.
In ∆ODE, OD = OE
∠ODE = ∠OED = y°.
ADEC is a cyclic quadrilateral.
∴ ∠CAD + ∠DEC = 180°
x + a + x + y = 180
2x + a + y = 180
y = 180 – 2x – a ……….. (iv)
But, ∠DOE = 180 – 2y
∠AOC = 180 – 2a

Question 5.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.

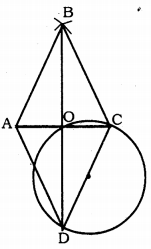
Solution:
Data: ABCD is a rhombus. Circle is drawn taking side CD diameter. Let the diagonals AC and BD intersect at ‘O’.
To Prove: Circle passes through the point ‘O’ of the intersection of its diagonals.
Proof: ∠DOC = 90° (Angle in the semicircle) and diagonals of rhombus bisect at right angles at ‘O’.
∴ ∠DOC = ∠COB = ∠BOA = ∠AOD = 90°
∴ Circle passes the point of intersection of its diagonal through ‘O’.

Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.

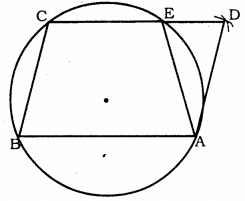
Solution:
Data: ABCD is a parallelogram. The circle through A, B, and C intersect CD at E. AE is joined.
To Prove: AE = AD
Proof: ∠AEC + ∠AED = 180° …………. (i) (linear pair)
ABCE is a cyclic quadrilateral.
∴ ∠ABC + ∠AEC = 180° ………….(ii) (opposite angles)
Comparing (i) and (ii),
∠AEC = ∠AED = ∠ABC + ∠AEC
∠AED = ∠ABC ………….. (iii)
But, ∠ABC = ∠ADE (Opposite angles of quadrilateral)
Substituting in equation (iii),
∠AED = ∠ADE
∴ AE = AD.

Question 7.
AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
Solution:
Data : AC and BD are chords of a circle bisect each other at ‘O’.
To Prove:
i) AC and BD are diameters.
ii) ABCD is a rectangle.
Construction: AB, BC, CD and DA are joined.

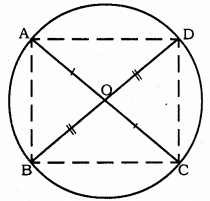
Proof: In ∆AOB and ∆COD,
AO = OC (Data)
BO = OD (Data)
∠AOB = ∠COD (vertically opposite angles)
∴ ∆AOB ≅ ∆COD (SAS postulate)
∴ ∠OAB = ∠OCD
These are pair of alternate angles.
∴ AB || CD and AB = CD.
∴ ABCD is a parallelogram.
∴ ∠BAD = ∠BCD (Opposite angles of parallelogram)
But. ∠BAD + ∠BCD = 180 (∵ Angles of cyclic quadrilateral)
∠BAD + ∠BAD = 180
2(∠BAD) = 180
∴ ∠BAD = \(\frac{180}{2}\)
∴ ∠BAD = 90°.
If angles of a quadrilateral are right angles it is rectangle. ABCD is a recrtangle.
∠BAD = 90°
∠BAD is separated from chord BD.
∴ This is the angl in semicircle.
∴ Chord BD is a diameter.
Similarly, ∠ADC = 90°
∴ Chord AC is a diameter.

Question 8.
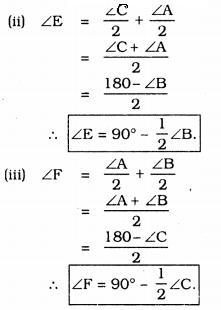
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – \(\frac{1}{2}\) A, 90° – \(\frac{1}{2}\) B and 90° – \(\frac{1}{2}\) C.
Solution:
Data: AD, BE and CF are angular bisectors of angles A, B and C of ∆ABC intersects its circumference at D, E and F respectively.

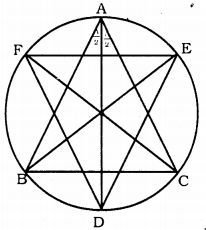
To prove: Angles of ∆DEF are 90° – \(\frac{1}{2}\) A, 90° – \(\frac{1}{2}\) B and 90° – \(\frac{1}{2}\) C.
Proof: AD, BE and CF are angular bisectors of angles A, B and C of ∆ABC.
∴ ∠BAD = ∠CAD = \(\frac{\angle \mathrm{A}}{2}\)

Question 9.
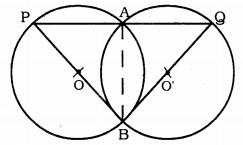
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lies on the two circles.
Prove that BP = BQ.

Solution:
Data : Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles.
To Prove: BP = BQ
Construction: Join AB.
Proof: Two congruent triangles with centres O and O’ intersects at A and B. Through A segment PAQ is drawn so that P, Q lie on the two circles.
Similarly, ∠AQB= 70° in circle subtended by chord AB. Because Angles subtended by circumference by same chord.
∴ ∠APB = ∠AQB = 70°.
Now, in ∆PBQ, ∠QPB = ∠PQB.
∴ Sides opposite to each other are equal.
∴ BP = BQ.

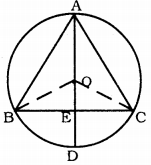
Question 10.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.

Solution:
Data: In ∆ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect each other. O is the centre of the circle.
To Prove: Angle bisector of ∠A and perpendicular bisector of BC intersect at D.
Construction: Join OB, OC.
Proof: Angle subtended at the Centre
= 2 × angles subtended in the circumference.
∠BOC = 2 × ∠BAC
In ∆BOE and ∆COE,
∠OEB = ∠OEC = 90° (∵ OE⊥BC)
∴ BO = OC (radii)
OE is common.
∴ ∆BOE ≅ ∆COE (RHS postulate)
But, ∠BOE + ∠COE = ∠BOC
∠BOE + ∠BOE = ∠BOC
2∠BOE = ∠BOC
2∠BOE = 2∠BAC
∴ ∠BOE = ∠BAC
But, ∠BOE = ∠COE = ∠BAC
∠BAD = \(\frac{1}{2}\) ∠BAC
∠BAD = \(\frac{1}{2}\) ∠BOE
∠BAD = \(\frac{1}{2}\) ∠BOD
∴ ∠BOD = 2∠BAD
∴ The angle subtended by an arc at the centre is double the angle subtended by it at any point on the circumference.
∴ Angle bisector of ∠A and perpendicular bisector of BC intersect at D.

KSEEB Solutions for Class 9 Maths