Students can Download Maths Chapter 7 Rational Numbers Ex 7.4 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 7 Rational Numbers Ex 7.4
1. Represent the following rational numbers on the number line.
Question (i)
\(\frac{-8}{5}=-2 \frac{2}{3}\)
Answer:
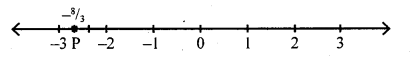
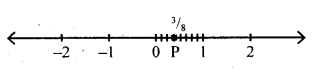
Question (ii)
\(\frac { 3 }{ 8 }\)
Answer:
Question (iii)
\(\frac { 2 }{ 7 }\)
Answer:

Question (iv)
\(\frac{12}{5}=2 \frac{2}{5}\)
Answer:
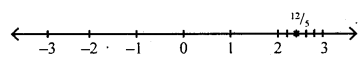
Question (v)
\(\frac{45}{13}=3 \frac{6}{13}\)
Answer:

Question 2.
Write the following rational numbers in ascending order.
\(\frac{3}{4}, \frac{7}{12}, \frac{15}{11}, \frac{22}{19}, \frac{101}{100}, \frac{-4}{5}, \frac{-102}{81}, \frac{-13}{7}\)
LCM of the denominators in 35550900
Answer:


= 66023100 < 44767800 < 2840720 < 20737850 < 26663175 < 35906409 < 41164200 < 48478500
∴\(\frac{-13}{7}<\frac{-102}{81}<\frac{-4}{5}<\frac{7}{12}<\frac{3}{4}<\frac{101}{100}<\frac{22}{19}<\frac{15}{11}\)
Question 3.
Write 5 rational number between \(\frac { 2 }{ 5 }\) and \(\frac { 3 }{ 5 }\) having same denominator.
Answer:
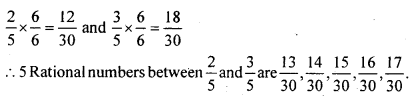
Question 4.
How many positive rational numbers less than 1 are there such that the sum of the denominator and numerator does not exceed 10?
Answer:
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \frac{1}{7}, \frac{1}{9}, \frac{1}{3}, \frac{2}{3}, \frac{2}{3}, \frac{2}{5}, \frac{2}{4}, \frac{3}{4}, \frac{3}{5}, \frac{3}{7}, \frac{4}{5}\)
are lesser than 1. There are 15 rational numbers.
Question 5.
Suppose \(\frac { m }{ n }\) and \(\frac { p }{ q }\) are two positive numbers. Where does \(\frac{m+p}{n+q}\) lie, with respect to \(\frac { m }{ n }\) and \(\frac { p }{ q }\) .
Answer:
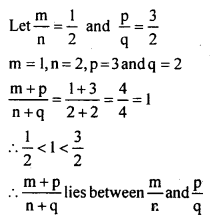
Question 6.
How many rational numbers are there strictly between 0 and 1 such that the denominator of the rational number is 80?
Answer:
Rational numbers with denominator 80 and numerator from 1 to 79 \(\left(\text { like } \frac{1}{80}, \frac{2}{80},-\cdots-\frac{79}{80}\right)\)
There are 79 such rational numbers.