Students can Download Maths Chapter 14 Introduction of Graphs Ex 14.1 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 14 Introduction of Graphs Ex 14.1
Question 1.
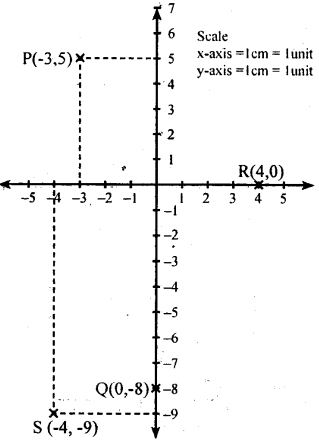
Fix up your own coordinate system on a graph paper and locate the following points on the sheet,
i. P(-3,5)
ii. Q(0,-8)
iii. R(4,0)
iv. S (-4, -9)
Answer:
Question 2.
Suppose you are given a coordinate system to determine the quadrant in which the following points lie.
Answer:
i. A (4, 5) – I Quadrant
ii. B (-4, -5) – III Quadrant
iii. C (4, -5) – IV Quadrant
Question 3.
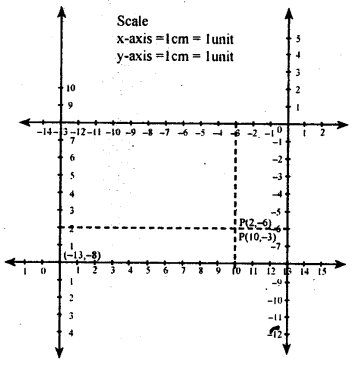
Suppose p is a point with coordinate (-8, 3) with respect to a coordinate system X1 O X → Y1 OY. Let X11 O1 X1 ↔ Y1OY be another system with X1OX || X11O1X1 and O1 has coordinates (9,5) with respect to X1OX ↔ Y1O Ywhat are the coordinate of p in the system X11 O1X1 Y11O1Y1?
Answer:
Let (x1 ,y1) be the coordinates point p in X11 O1 X1 ↔ Y1OY.
Then x = a + x1 and y = b + y1
but (a, b) = (9, 5)
∴ – 8 = 9 +x1 y = b + y1
– 8 – 9 = x1 3 = 5 + y1
-17 = x1 3 – 5 = y1
∴ (x1 , y1 ) = (-17,-2)
∴ Coordinatesof pin X11 O1 X1 ↔ Y1OY are (-17,-2)
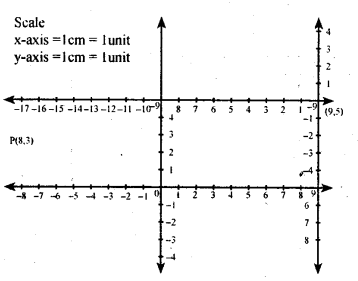
Question 4.
Suppose P has coordinates (10,2) in a coordinate system X’OX ↔ Y’OY and (-3,-6) in an other coordinates system X’1O1 X↔Y’1O1X1. Determine the coordinates of O with respect to the system X’1 O1 X1 || Y’1 O1Y1’.
Answer:
Given p(x , y) = (10 , 2), (x’, y’) = (-3, -6)
Let the coordinates of O, in
X’1O1 X1 ↔ Y’1O1 Y1 be (a,b) then
x = a + x1 y = b + y1
10 = a + (-3) 2 = b + (-6)
10 = a – 3 2 = b – 6
10 + 3 = a 2 + 6 = b
a = 13 b = 8
Coordinates of O1 in
X’1 O 1Y1, ↔ Y1 O 1Y’1 is (13 , 8) we should find the coordinates of O
(0, 0) in X’1O 1X1↔ Y’1O1Y1
Let (x , y) = (0 , 0) , (x’, y’) = (13 , 8) .
(a ,b) = ? y = b + y’
0 = a + 13 0 = b + 8
-13 = a -8 = b
(a = – 13) b= -8
The coordinates of O w.r.t to
X’1 O 1Y1, ↔ Y1 O 1Y’1 are (-13 , -8).