You can Download Chapter 5 Theoretical Distribution Questions and Answers, Notes, 2nd PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Question Bank Chapter 5 Theoretical Distribution
2nd PUC Statistics Theoretical Distribution One and Two Marks Questions and Answers
Question 1.
Write down the probability mass function of a Bernoulli distribution.
Answer:
The Bernoulli distribution is:-
P(x) = PX( 1 – P)1 – X. where P> O, and X = 0,1;
OR p(x) = Pxq1 – X; x = o,1 (Range); .
P-parameter, Mean = p, Variance = P(1 – p) 0r pq; mean> variance
Ex:- (i) A coin is tossed & getting H or T
(ii) A new born baby is a male or female ¡s a Bernoulli variate with the parameter P = 0.5.
Question 2.
Write down the p.m.f of Binomial distribution and with its two features and examples.
Answer:
The Binomial distribution is:- P(x) = ncx px qn-x;
Featurcs: Where x = 0,1,2,3… n and d 0 < P < 1
Range – 0, 1, 2 n; Mean = np, var(x) = npq; rnean>variance, le., np > npq;
![]()
B.D is symmetrical when p = 1/2
Ex:- Ñurnber of Heads obtained when 5 coins are tossed / Number of male children in a family of 5 children.
Question 3.
Write down the p.m.f of Poisson distribution and with its two features and examples.
Answer:
The Poisson distribution is P(x) = \(\frac{\mathrm{e}^{-\lambda} \lambda^{\mathrm{x}}}{\mathrm{x} !}\) ;x = 0,1,2…∞ ,& λ >0
Range = (0, oo ), λ – parameter, Mean = λ, Var = λ; Mean = Variance.
Theoretical Frequecy: Tx = \(\frac{\lambda}{\mathrm{x}}\) Tx-1
Ex:- Number of telephone calls received by a receptionist/ Number of printing mistakes in book of 200 pages
Question 4.
Write down the p.m.f of Hyperegeometric distribution and with its two features and examples.
Answer:

Hypergeometric distribution tends to Binomial distribution when:
- a is large ie.a → ∞
- b is large ie. b → ∞ and
- \(\frac{\mathrm{a}}{\mathrm{a}+\mathrm{b}}\) = p is fixed.
`Ex:- Number of vegetarians in an office of 18 vegetarians and 12 non-vegetarians; number of apples selected from a bag containing 20 oranges and 10 apples.
![]()
Question 5.
Write down the p.m.f of Normal distribution and with its two features and examples.
Answer:
The Normal distribution is:-
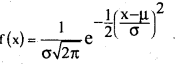
Where -∞ < x < ∞, (Range) σ > 0
Ht./Wt.of students of a class; I.Q.of a large group of children; Wages/Income of employees
Properties:-
- Curve is bell shaped, Mean = Median = Mode ie., The curve is Symmetric ie., non-skew (β1 = 0)
- Mean = µ, Variance = σ2; S.D = σ, Q.D = 2/3 σ, M.D = 4/5 σ
- The curve is Mesokurtic β2 = 3
- The area under the Normal curve is 1
- The curve is asymptotic to the x-axis, ie. It touches the x-axis at -∞ and ∞,
- Q1 & Q3 are equidistant from: X̄ / M / Z = \(\frac{\mathrm{Q}_{3}+\mathrm{Q}_{1}}{2}\)
Question 6.
Write down the p.m.f of Chi-square distribution and students t – distribution with its two features and examples.
Answer:
Chi-square distribution:-
Definition-Let Z1, Z2, Z3, Zn are n S.N.V’s;
Then X2 = Z12+ Z22 + Z32 …….+ Zn2 ~ X2 (n)
Features/Properties:- parameter ‘n’; Mean = n, Variance = 2n.
Mode = (n – 2) for n > 2, Range – (0, ∞ ); The curve is + vely Skewed.
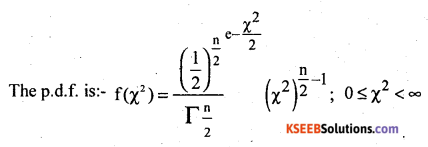
Application/uses:-
- Test for population variance;
- Test for Goodness of fit
- Test for Independence of Attribute.
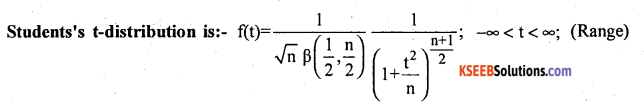
Properties : – n – parameter, Mean = 0, (X̄ = M = Z = 0),
Variance = \(\frac{n}{n-2}\) for n>2, -∞ < t < ∞;
Application:-
- To test for Population mean
- Test for equality of means,
- Test for equality of two population’s means when observations are paired (paired t-test).
Question 7.
What are Bernoulli trials?
Answer:
A random experiment which has only two outcomes as, success and failure with P(success)=P, and P(failure) = q = 1 – P, is called Bernoulli experiment/Trial.
Question 8.
What are the Mean and Variance of a Bernoulli distribution?
Answer:
Mean = p, Variance = P(1 – P).
Question 9.
For a Bernoulli distribution, parameter p = 1/4, the write its p.m.f.
Answer:
P(x) = ( 1 / 4)x (1 – 1 / 4,)1-x , x = 0,1
![]()
Question 10.
Write the Bernoulli distribution with parameter p = 0.23.
Answer:
P(x) = (0.23)x (1 – 1/4,)1-x , x = 0.1
Question 11.
Parameter of Bernoulli distribution is 0.2. What is its mean?
Answer:
Mean: p = 0.2
Question 12.
What are the values that a Bernoulli variate can take?
Answer:
Range: 0.1
Question 13.
If p = 1/3, for Bernoulli distribution, write down mean & variance
Answer:
Mean = p = 1/3 and variance = p(1-p) = 1/3(1 – 1/3) = 0.2211
Question 14.
Mention any two features/properties of a Binomial distribution.
Answer:
- BD has parameters,
- Mean = np,/variance = npq, Here Mean>variance,
- BD.is symmetric when p=q.
Question 15.
If a Binomial distribution has mean = 12 and Sd = 3, obtain the values of n and p.
Answer:
![]()
Question 16.
In a Binomial distribution mean = 7 and variance = 11. Is the above statement correct?
Answer:
Since Mean > Variance, the statement is not correct.
Question 17.
Is mean of Binomial distribution is less than variance
Answer:
No, mean is greater than variance.
Question 18.
For a B.D. mean is 4 and S.D is √2 Find the parameters
Answer:
\(\mathrm{S.D}=\sqrt{\mathrm{var}}=\sqrt{\mathrm{npq}}=\sqrt{2}\) ; squaring both sides; npq = 2; 4q = 2;
∴q = 0 ∴ 5, p = 0.5 & put p = 0.5 in np = 4; ∴ n = 8
Question 19.
In a Binomial distribution with 5 trials the mean is 3. Find P and its variance.
Answer:
n = 5, Mean = np = 3
Put n = 5 in np = 3; 5p = 3; p = 3/5 = 0.6;
P = 0.6; Var(X) = npq = 5 x 0.6(1 – 0.6) = 5 x 0. 6 x 0.4 = 1.2
Question 20.
For what value of ‘p’ in B.D is Symmetrical?
Answer:
P = 1/2 = 0.5 B.d is symmetrical
Question 21.
In a Binomial distribution, if n = 6 and P = 1/3 find the mean.
Answer:
Mean = E(x) = np = 6 × 1/3 = 2
Question 22.
In a Binomial distribution, if n = 8 and mean = 2, find p.
Answer:
Mean = np = 2, 8p = 2; p = 2/8 = 0.25 ie. P = 0.25
![]()
Question 23.
“The mean and variance of Binomial distribution are 4 and 5 respectively” comment on this statement and give reason to your comment:
Answer:
For a Binomial Variate Mean > Variance;but here Mean(4) < Variance (5), statement is incorrect.
Question 24.
Mention any two properties of Poisson distribution
Answer:
λ is parameter; Mean = λ; var (x) = λ, Here Mean = Var (x);
Question 25.
Find p(x = 0) in Poisson distribution with mean 5 e 3
Answer:
\(\frac{\mathrm{e}^{3} 3^{0}}{0 !}\) = 0.0498
Question 26.
In the following p.m.f: p(x) = \(\frac{e^{-3} 3^{x}}{x !}\) ; what is variance?
Answer:
Given λ, = 3; variance = λ = 3
Question 27.
If X is a Normal variate, then what is the value of P(x ≥ μ) OR What is the probability that a Normal variate takes a value greater than its Mean?
Answer:
0.5.
Question 28.
If ‘Z’ is a standard normal variate, find k such that p(z > k) = 0. 4.
Answer:
1.28
Question 29.
Find the area under the Normal curve between Z = – 1.7 and Z = + 1.7
Answer:
2(Area from 0 to 1.7) = 2(0.4554) = 0.9108.
Question 30.
In a Poisson distribution, the first probability term is 0.2725. Find the next probability term.
Answer:
p(x = 0) = 0.2725; ie. e-λ λ0 = 0.2725; e-λ = 0.2725; ∴ From the table X = 1.3.
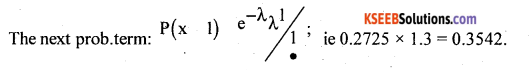
Question 31.
In a Poisson distribution, if P(x = 0) = 0.0408, find λ.
Answer:
from the table λ = 3.
Question 32.
Define S.N.V.AVhat do you mean by SNV?
Answer:
A normal variate with mean µ = 0 and S.D. σ2 = 1 is called S.N.V.denoted by
Z = missing ~N(0,l)
Question 33.
What is the area under the normal curve?
Answer:
Total area under the normal curved is one i.e. 1
![]()
Question 34.
What are the mean and variance of Standard Normal distribution?
Answer:
Mean µ = 0 and variance σ2 = 1
Question 35.
Write the S.D. of SNV.
Answer:
σ = 1
Question 36.
The Quartiles Q1 and Q3 of Normal distribution are 30 and 60 respectively. Find mode.
Answer:
In a Normal distribution the two quartiles are equidistant from the median/ mean / mode.
Mode mode (Z) = \(\frac{\mathrm{Q}_{3}+\mathrm{Q}_{1}}{2} \quad \frac{30+60}{2}=45\) = 45
Question 37.
Find Q.D and M.D.of Normal distribution with mean 30 and S.D.6.
Answer:
For a Normal distribution QD = \(\frac{2}{3} \times \sigma=\frac{2}{3} \times 6\) = 4,
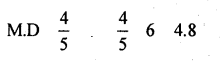
Question 38.
If S.D of a Norrmal distribution is 15, find QD and MD
Answer:
For a Normal distribution QD. = \(\frac{2}{3} \times \sigma=\frac{2}{3} \times 6\) = 4,
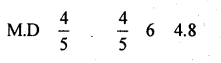
Question 39.
For a normal distribution if variance is 9. Find its Q.D.
Answer:
Variance : σ2 = 9, ∴ σ = 3;
For a Normal distribution Q.D \(\frac{2}{3}\) \(\frac{2}{3}\) 3 2
Question 40.
What are the values of β1 and β2 in a Normal distribution?
Answer:
β1 = 0 and β2 = 3
Question 41.
What is mean of t-distribution?
Answer:
Mean = 0.
![]()
Question 42.
The distribution of variable is given by the law:
Answer:
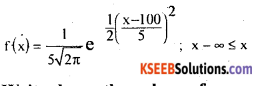
Write down the values of mean and standard deviation.
Answer:
Mean = μ = 100, σ = 5
Question 43.
Write down the probability function of a Normal variate which has mean 8 and variance 9.
Answer:
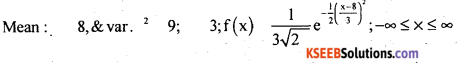
Question 44.
Define – variate for n d.f.and mention its mean, variance.
Answer:
Let Z1, Z2, Z3,…Zn be n independent SNV’s , Then,
χ2 = Z12,+ Z22 + Z32, …. + Zn2 is a χ2 – variate with n d.f; Mean = n, Var (x) = 2n
Question 45.
In an N.D. variance is 9cm2, find Q.D.
Answer:
Q.D = 2/3 , x = 2/3 x3 = 2.
Question 46.
If Z1, Z2, Z3 are 3 independent S.N.V’s then what is the distribution of (Z12 + Z22 + Z32)?
Answer:
It is a χ2 – distribution with 3 d.f.
Question 47.
If Z is a SNV, Name the distribution of Z2, its variance.
Answer:
Chi-square distribution and variance = 2n = 2 × 1 = 2
Question 48.
X is a Normal variate with mean = 25, and S.D = 5. What are the probability distribution of
\(\left(\frac{x-25}{5}\right)\) and \(\left(\frac{x-25}{5}\right)^{2}\)
Answer:
It is SNV~N(0,1), ie Normal distribution, and χ2 – distn with 1 d.f.
Question 49.
If X is Normal variate with mean 15 and Variance 4. What are the probability distribution of
(i) Z
(ii) Z2 Where Z = \(\frac{x-15}{2}\) ?
Answer:
(i) Z~ N(0,l)
(ii) Z2 ~ χ2(1)
![]()
Question 50.
If Z1 and Z2 are two independent standard normal variates thgen name the distribvution of Z12 + Z22. Find its mode.
Answer:
It is a χ2 – distribution with 2 d.f. ie., χ2 (2); Mode (z) = (n – 2) for n ≥ 2; Mode = 2-2 = 0
Question 51.
If χ3 (3) = Z12 + Z22 + Z32 find variance.
Answer:
Given : n(d.f) = 3; variance = 2n = 2 × 3 = 6.
Question 52.
If mean of χ3 -distributions is 6, and then find its S.D.
Answer:
![]()
Question 53.
If the variance of χ2 – variate is 12? What is its Mean?
Answer:
Variance = 2n = 12, mean = n = 6.
Question 54.
Write down the mean and range of chi-square distribution
Answer:
Mean = n, Range is (0, ∞ ) or 0 to ∞ .
Question 55.
What is the parameter of the χ2 – distribution with n d.f.?
Answer:
n d.f.
Question 56.
The degrees of freedom of Chi-square variate is 7. Find its Mean, mode and variance.
Answer:
n = 7, mean = n = 7, Mode = (n – 2) = 5 and Variance = 2n = 2 × 7 = 14.
Question 57.
What d.fiis used in testing the independence of attributes and Goodness of fit?
Answer:
1 d.f.; (n-1) & (n-2)
Question 58.
If the parameter of t-distribution is 6, find the-variance.
Answer:
Variance = \(\frac{n}{n-2}-\frac{6}{6-2}-1.5\)
Question 59.
If the parameter of t-distribution is 4 or 6. Find the variance.
Answer:
Variance = \(\frac{n}{n-2}-\frac{6}{6-2}-1.5\)
Question 60.
If a = 5, b = 15 and n = 3, then find the variance of hyper-geometric distribution.
Answer:
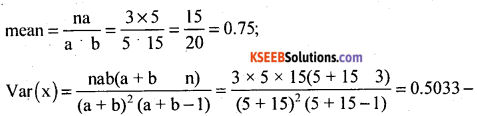
Question 61.
Write down the p.m.f. and mean of a hyper-geometric distribution whose parameters are a = 4, b = 7 and n = 5.
Answer:

Question 62.
For a hyper-geometric distribution the parameters are a = 7, b = 5 and n = 8. What is the range of the hyper-geometric distribution? Also find the S.D.
Answer:
Range is min(a,n) = 0, 1, ,7;
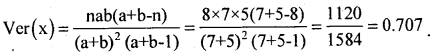
Question 63.
Define a poisson variate.
Answer:
A probability distribution which has the following probability mass function as:’
\(\mathrm{P}(x)=\frac{e^{-\lambda} \lambda^{x}}{x}\) , x = 0,1,2,…../λ > 0
Question 64.
If variance of χ2 variable is 12, What is its mean?
Answer:
Mean = n, Variance = 2n
i.e., 12 = 2n ; n = 6, Mean = 6
Question 65.
If Z is a SNV indicate the value of P [Z > 0].
Answer:
Area from 0 to ∞ = 0.5.
![]()
Question 66.
If S.D. of a poisson variate is 2, then obtain its mean.
Answer:
![]()
2 = √ λ ∴ λ = 4.; ∴ Mean = 4.
Question 67.
If X is a Poisson variate with mean 3, what is its standard deviation ? {June-2008)
Solution:
Given, mean = variance = λ = 3.
![]()
Question 68.
If x is a Normal variate, then what is the value of P[x > z]?
Answer:
In a normal curve, Mean = Median = mode.
∴ P [x > µ] = P [ z > 0] = 0.5
Question 69.
Write the p.d.f of a normal variable with mean 10 and SD 2.
Answer:
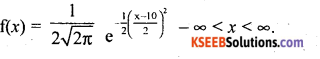
Question 70.
Write the condition that Binomial distribution tends to Normal distribution.
Answer:
(a) n is large (n → ∞)
(b) neither p nor q is very small.
Question 71.
Write any one property of chi square distribution.
Answer:
Mean = n.
Question 72.
What is the parameter of the chi-square distribution with n degrees of freedom?
Answer:
parameter – n.
Question 73.
χ2 – distribution is derived from which distribution?
Answer:
Normal distribution.
Question 74.
Find the mean and standard deviation of the following probability density function
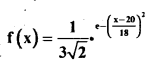
Answer:
This is the p.d.f of normal distribution. Here µ = 20, σ = 3.
Question 75.
Give the mean and mathematical equation of normal probability curve.
Answer:
The probability density function or equation of a normal curve.
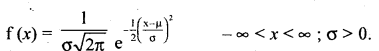
Question 76.
In a poisson distribution the mean is 4, then find its variance.
Answer:
In poisson distribution mean = variance ∴ variance = 4.
Question 77.
In a Binomial distribution, If n = 6 and P = \(\frac{1}{3}\) , find mean.
Answer:
Mean = E(x) = np = \(6 \times \frac{1}{3}\) =2
![]()
Question 78.
In a Poisson distribution if standard deviation is 3″ , the find the mean.
Answer:
Given S.D = √variance = 3
Squaring on both sides
variance = 9
In Poisson distribution mean = variance
∴ mean = 9
Question 79.
Name the distribution in which mean and variance are equal.
Answer:
Poisson distribution.
Question 80.
Give an example for Normal variate.
Answer:
Height/weight of students in a class.
Question 81.
Write the relation between mean and variance of Bernoulli Distribution.
Answer:
mean > variance
i.e., P > P (1 – P)
Question 82.
In a Binomial distribution, if n = 8 and mean = 2, find p.
Answer:
For a Binomial variate mean = nP
Given ,2 = 8p
P = \(\frac{2}{8}\) = 025
Question 83.
If Z is a standard normal variate, then what is the distribution of Z2 ?
Answer:
Z2 ~ χ2(1) i.e., It is a chi-square distribution with 1 degree of freedom.
Question 84.
Define degrees of freedom.
Answer:
Number of independent variable components of the chi-square distribution is called degrees of freedom.
Question 85.
For a Bernoulli distribution parameter P = \(\frac{1}{4}\), find its standard deviation.
Answer:
For a Bernoulli variable x :

Question 86.
If a Binomial distribution has mean 12 and SD 3. Obtain the values of n and p.
Answer:
Mean = np = 12

∴q = 3/4
∴ P = 1 – q = 1/4. Put P = 1/4 in np = 12 n x 1/4 = 12
∴ n = 48
Question 87.
Name probability distributions which are most appropriately used in the case of
(a) No. of male children in a family of 5 children.
(b) No. of telephone calls received at a telephone exchange between 9 am And 10 am.
Answer:
(a) Binomial Distribution.
(b) Poisson Distribution.
![]()
Question 88.
If Z is a standard Normal variate, find k such that P[Z > k] = 0.10.
Answer:
Area from K to ∞ = 0.10
Area from 0 to k = 0.5 – 0.10 = 0.4
∴ From the table k = 1.28
Question 89.
For a poisson distribution p[x = 0] = p[x = 1] ; Find mean.
Answer:
p[x = 0] = p [x = 1]
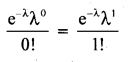
1 = λ ∴ Mean = λ = 1
Question 90.
In a Poisson distribution, the first two frequencies are 100 and 120 respectively. Find the next frequency.
Answer:
Given : T(x = 0) =100; T(x = 1) = 120

Question 91.
Write down mean and S.D of χ2 – variate with 8 d.f.
Answer:
Mean = n = 8.
![]()
Question 92.
Mention any two properties of Normal distribution.
Answer:
(a) The curve is symmetrical β1 = 0. (A)The curve is Mesokurtic β3 = 3.
Question 93.
State any two properties of χ2 – distribution.
Answer:
Range = (0, ∞), Mean = n, Variance = 2n.
Question 94.
Mention any two properties of the Binomial distribution?
Answer:
(i) Mean = np; Variance = npq.
Question 95.
Under which conditions, Binomial distribution tends to Poisson distribution?
Answer:
Binomial distribution tends / leads to Poisson distribution when
(a) n is large i.e., n → ∞
(b) p is very small i.e., P → 0 and
(c) mean = np = λ is the parameter of Poisson distribution.
Question 96.
Under what conditions Binomial distribution tends to poisson distribution?
Answer:
(a) n is large (i.e., n → ∞ ) (b) P is very small (p → 0)
(c) And np = λ is fixed.
Question 97.
Under what conditions does Binomial distribution tend to Normal distribution?
Answer:
(a) When n is large i.e., n → ∞
(b) Neither p nor q are very small and mean = np = µ , S.D = \(\sqrt{n p q}\) = ‘σ’ are the parameters of Normal distribution.
![]()
Question 98.
Find the area under the standard normal curve for P [1 < Z < 2.5].
Answer:
Area from 0 to 2.5 – Area from 0 to 1.
= 0.4938 – 0.3413 = 0.1525.
Question 99.
If mean of Bernoulli distribution is P, then find its standard deviation.
Answer:
![]()
Question 100.
Ifx is a Normal variate with mean 15 and variance 4, what is the probability distribution of (i) Z and (ii) Z2, when Z = \(\frac{x-15}{2}\) ?
Answer:
(i) Normal distribution
(ii) χ2 – distribution with 1 degree of freedom.
Question 101.
What is the relationship between mean and variance in a Binomial distribution?
Answer:
Mean > Variance ; i.e., np > npq.
Question 102.
A Bernoulli variate takes a value 1 and 0 with probabilities 0.2 and 0.8 respectively. Find the mean and variance.
Answer:
The probability distribution is:
![]()
Mean = P = 0.2 .
Variance = P(1 – P) = 0.2 x 0.8 = 0.16
Question 103.
In a Normal distribution if the values of Q1 and Q3 are 25 and 55 respectively. Find Mean.
Answer:
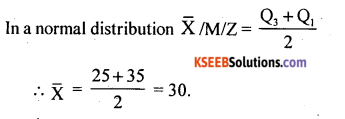
Question 104.
Define Standard Normal Variate.
Answer:
A Normal variate with mean µ = 0 and SD = σ = 1 is called a SNV. It is denoted by Z. Its
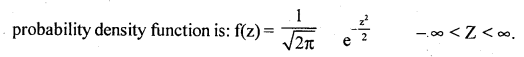
Question 105.
If mean is 10 and standard deviation is 2 for a Normal distribution, find quartile deviation and mean deviation.
Answer:
For the normal distribution-
Quartile deviation = \(\frac{2}{3}\) σ = \(\frac{2}{3}\) .2 = 1.33.
Mean deviation = \(\frac{4}{5}\) = \(\frac{4}{5}\).2 = 1.6
Question 106.
Find the mean and mode of a χ2 = distribution with 7 degrees of freedom.
Answer:
For a χ2 – distribution; mean = n = 7; mode = (n-2) = 7- 2 = 5.
Question 107.
If variance of normal distribution is 9 sq.cms, then find the quartile deviation.
Answer:
Variance = σ2 = 9 ∴σ2 = √9 = 3.
In a normal distribution quartile deviation = \(\frac{2}{3} \sigma=\frac{2}{3} \times 3=2\)
![]()
Question 108.
What are Bernoulli trials? / Define Bernoulli Experiment.
Answer:
A random experiment has only two out comes as ‘success’ and ‘failure’. With the probability of success as ‘p’ and probability failure as ‘q’ is called Bernoulli trial or Bernoulli experiment.
Question 109.
If n = 5; P = 0.3, write down the probability function of Binomial distribution. Answer: The p.m.f of Binomial distribution is:
p(x) = n cx px qn-x; x = 0,1,2, …………n.
Here n = 5, p = 0.3 ; ∴ q = 1 – p = 0.7.
∴ p(x) = 5cx 0.3x 0.75-x; x = 0, 1, 2, ……….. 5.
Question 110.
If x follows a poisson distribution with mean 3, then find the p[x = 0].
Answer:
Given λ = 3

Question 111.
In a normal curve, what is the percentage area formed in the 1.96a neighbourhood of µ.
Answer:
In normal distribution 1.96 a neighbourhood of mean is:
p [µ – 1.96 σ < x < µ + 1.96 σ]
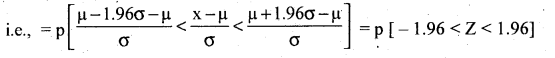
= Area from 0 to (-1.96) + Area from 0 to 1.96.
∴ From the table
= 0.4750 + 0.4750 = 0.9500
∴ The percentage area is : 0.9500 x 100 = 95%
Question 112.
Find the area under the normal curve with mean 0 and variance 1 that lies between (-1.64) and 1.64.
Answer:
Here z~N(0, 1)
∴ p[-1 .64 < Z < 1.64] = Area from 0 to (-1.64) + area from 0 to 1.64
∴ From the table = 0.4495 + 0.4495 = 0.899.
Question 113.
If x is a Binomial variate with n = 8 and P = 1/2 , then find the value of p[x =1].
Answer:
Given: n = 8, p = 1/2 ∴ q = 1 – p = 1/2.
The p.m.f of Binomial distribution is
∴ p(x) = ncx px qn-1:; x = 0, 1, 2 …………. n.
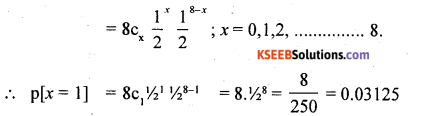
Question 114.
If Z1, Z2 and Z3 are 3 independent standard normal variates, then what is the distribution of Z12 + Z22 + Z32?
Answer:
Here Z12 + Z22 + Z32 is a chi-square distribution with 3 degrees of freedom, i.e., χ(3)2
Variance = 2n = 2.3 = 6.
![]()
Question 115.
Find the mean and mode of a %2 – distribution with 7 degrees of freedom.
Answer:
For a χ2 – distribution, mean = n = 7.
Given n = 7. Mode = (n – 2) for n > 2.
∴ Mode = (7 – 2) = 5
Question 116.
Write down the reccurence relation to find the successive theoretical frequencies in
Answer:

Question 117.
Write down the area properties of a normal distribution.
Answer:
(a) The total are under the normal curve is unity.
(b) p [µ – σ < x< µ + σ] = 0.6826.
(c) p [ µ – 2σ < x < µ + 2σ] = 0.9544.
(d) p [µ – 3σ < x < µ + 3σ] = 0.9974.
Question 118.
What are the mean and variance of a normal distribution?
Answer:
Mean = µ ; Variance = σ2.
![]()
Question 119.
What are the mean and variance of the standard normal variate?
Answer:
Mean = µ = 0 ; Variance = σ2 = 1.
Question 120.
Find the area that lies between 0.4 and 0.8 in a normal curve.
Answer:
i.e.,p[0.4 < z < 0.8]
= Area from 0 to 0.8 = Area from 0 to 0.4
= 0.2881 -0.1554 =0.1327.
Question 121.
If the parameter of /-distribution is 6, find the variance.
Answer:
For t – distribution, variance \(\frac{\mathrm{n}}{\mathrm{n}-2}\) for n>2
\(\frac{\mathrm{6}}{\mathrm{6}-2}\) = 1.5
Question 122.
For a Binomial distribution mean is 4 and standard deviation is √2 Find the parameters.
Answer:
Given : mean = np = 4

Question 123.
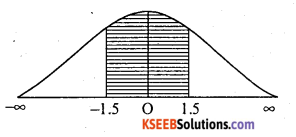
Find the area under the normal curve between z = -1.5 and z = +1.5 Answer: Area under the normal curve.
= Area from (-1.5) to 1.5 .
= Area from 0 to 1.5 + Area from 0 to (- 1.5)
= 0.4342 + 0.4342 = 0.8684
Question 124.
If p1 = 0.3 and p2 = 0.2, find mean of (p1 – p2).
Answer:
Mean of (p1 – p2) = E(p1 – p2) = 0.3 – 0.2 = 0.1
2nd PUC Statistics Theoretical Distribution Five Marks Questions and Answers
Binomial Distribution
Question 1.
A un biased coin is tossed 5 times. Find the probability of getting 2 heads and 3 tails.
Answer:
Let A- be the no. of heads obtained is a Binomial variable with parameters n = 5; p = 1/2 (since the coin, is unbiased). ∴ q = 1 – P = 1/2
The p.m.f is :
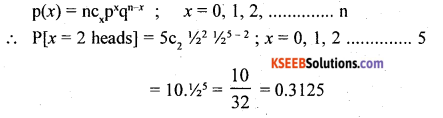
Question 2.
In a family of 4 children, find the probability of that 2 children are males. Given that birth of a male child and birth of a female child are equally likely.
Answer:
Let x denote the no. of male children is a Binomial variate with parameters n = 4, p = 1/2 (since birth of male and female child is equi probable) .∴ q = 1/2.
The p.m.f is-
p(x) = ncx px qn-x ; x = 0, 1, 2, ………… n
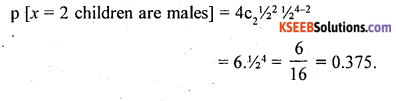
![]()
Question 3.
The probability that a gun shot hitting a target is 1/3. If five gun shots aimed at the target. Find the probability that 2 shots miss the target.
Answer:
Let x be the no. of shots hitting the target then n = 5, p = \(\frac{1}{3}\), ∴ q = \(\frac{2}{3}\)
The p.m.f is

Question 4.
If a fair die is thrown 4 times. If x denote the number of throws results in mutiple of 3. Then find mean and variance of x.
Answer:
Let x be the number of throws results in multiple of 3 is a Binomial variate with n = 4, p = p [a die thrown results in multiple of 3] =\(\frac{2}{6}\) = \(\frac{1}{3}\)
∴ q = \(\frac{2}{3}\)
Then, mean = np = 4 x \(\frac{1}{3}\) = 1.33.
Variance = npq = 4 x \(\frac{1}{3}\) x \(\frac{2}{3}\) = 0.889.
Question 5.
In an office 20% of the employees are females. In a random sample of 5 employees obtain the probability that there are – (a) no females (b) females only.
Answer:
Let x be the no. of the female employees is a Binomial variate with parameter n = 5.
p = p [an employee is a female] = 20% = 0.2. ∴ q = 1 – p = 0.8
The p.m.f. is –
p(x) =ncx px qn – x; x = 0,1,2, …… n
= 5 cx (0.2)x (0.8)5 – x ; x = 0,1,2, … 5
(a) p (no females) = p(x = 0)
= 5co (0.2)0 (0.8)5 – x
= 1 × 1 × 0.3277
= 0.3277
(b) p (females only) = p(x = 5)
= 5C5 (0.2)5 (0.8)5-5
= 1 × 0.00032 × 1
= 0.00032. .
Question 6.
2% of the blades manufactured by a firm are defective. Blades are supplied in packets of 5 each. What is the probability that randomly selected packet will have atleast one defective?
Answer:
Let x denote the number of defective blades is a Binomial variate with the parameters n = 5. p = p[blade is defective] = 2% = 0.02, ∴ q = 0.98.
The p.m.f is –
p(x) = ncx px qn – x; x = 0,1,2, …… n
= 5cx (0.02)x (0.98)5 – x; x = 0,1,2, …….. 5
p (packet has atleast one defective) = p(x ≥ 1)
= 1 – p (packet has no defectives)
= 1 – p (x = 0)
= 1 – 5c0 (0.02)0 (0.98)5-0
= 1 – 0.9039 = 0.0961
[Note: This problem can also be solved by poisson distribution.]
Question 7.
In an industry, the workers are having 25% chance of suffering from an occupational disease. Among 6 randomly selected workers, what is the probability that at most 2 will contract the disease?
Answer:
Let x be the number of workers contracting disease is a Binomial variable with parameters n = 6, p = p [a worker contract the disease] = 25% = 0.25.
∴ q = 0.75.
The p.m.f is –
P(x) = ncx px qn – x; x = 0,1,2, …… n
= 6cx 0.25x (0.75)6-x ; x = 0,1,2, …….. 6
p (at most 2 workers contract the disease)
= p(x ≤2)
= (x – 0) + p(x = 1) + p(x = 2)
= 6c0 (0.25)0 (0.75)6 – 0+ 6c1 (0.25)1 (0.75) 6 – 1 = 6c2 (0.25)2 (0.75) 6 – 2
= 1 ×1 × 0.1799 + 6 × 0.25 × 0.2373 + 15 × 0.0625 × 0.3164
= 0.1779 + 0.3559 + 0.2966
= 0.8304
![]()
Question 8.
In a village \(\frac{1}{3}\) of the people are literate. If 100 investigators meet 5 persons each to see if they are literates, then how many investogators would you expect to report that 2 or more were literates?
Answer:
Let x be the number of literate persons is a Binomial variate with parameters n = 5,
p = p (person is literate) = \(\frac{1}{3}\), ∴ q = 1 -p = \(\frac{2}{3}\); N=100
The p.m.f is –
P(x) = ncx px qn – x; x = 0,1,2, …… n
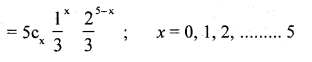
p(2 or more persons were literates)
= p(x ≥ 2)
= 1 – p (less than 2 persons were literates)
= 1 – p (x < 2) = 1 – p (x = 0) + p (x = 1)
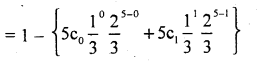
= 1 – {1 × 1 × 0.1317 + 5 × 0.3333 × 0.1975}
= 1 – {0.1313 + 0.3292}
= 1 -0.4605 =0.5395
Number of investigators = 0.5395 x 100 = 53.95 = 54
Question 9.
‘A’ has probability \(\frac{3}{5}\) of winning a game of chess with ‘B’ If they play four games find the probability that A wins (a) exactly one game (b) atleast 3 games.
Answer:
Let x be the number of games that ‘A’ wins, is a Binomial variate with parameters
n = 4, p = \(\frac{3}{5}\) , ∴ q = 1 – p = \(\frac{2}{5}\)
The p.m.f is –
P(x) = ncx px qn – x; x = 0,1,2, …… n
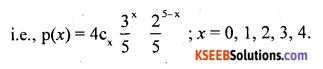
(a) p (A wins exactly one game)
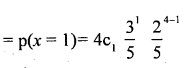
= 4 × 0.6 × 0.064
= 0.1536.
(b) p (A wins atleast 3 games)
= p(x ≥ 3) = p (x = 3) + p (x = 4)
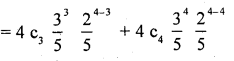
= 4 × 0.216 × 0.4 + 1 × 0.1296 x 1
= 0.3456 + 0.1296
= 0.4752.
Question 10.
The probability that a bomb hits a target is \(\frac{2}{5}\) . 4 bombs are aimed at a bridge. 3 bomb-hits are enough to destroy the bridge. Find the probability that
(i) the bridge is destroyed
(ii) none of the bombs hit the bridge.
Answer:
Let X be the number of bombs hitting a target is a binomial variate, with the parameters 2
= 4,. p = \(\frac{3}{5}\) = 0.4, q = 1 – p = 1- 0.4 = 0.6
The p.m.f is:
P(x) = ncx px qn – x; x = 0,1,2, …… n
= 4cx (0.4)x (0.6)4-x; x = 0,1,2,3,4.
(i) P (the bridge is destroyed)
= p(x ≥ 3) = p(x = 3) + p(x = 4)
=4C3 (0.4)3 (0.6)4 – 3+ 4C4 (0.4)4 (0.6)4 – 4 =0.1536 + 0.0256 =0.172
(ii) P (none of the bomb hit)
= p(x = 0) = 4C0 (0.4)0 (0.6)4 – 0 = 0.1296
![]()
Question 11.
The first and second probability terms of a binomial distribution are 0.0337 and 0.18, with n = 4 find P.
Answer:
Given:
First probability term: P(x = 0) = 0.0337
ie., 4co p0 q4 – 0 = 0.0337
1. 1. q4 = 0.03337 → (1)
Second probability term : P(x = 1) = 0.18
i.e., 4c1 p1 q4 – 1 = 0.18.
4 p q3 = 0.18 → (2)
(2) ÷ (1)

= (1 – p) 1.3353
p = 1.3353 – 1.3353p
p + 1.3353 p= 1.3353
2.3353p= 1.3353
P = \(\frac{1.3353}{2.3353}\) = 0.5718
Question 12.
In a binomial distribution with the parameters n = 3 and P, the second and the third frequency terms are 16 and 15 respectively. Find P.
Answer:
Given: Frequency term:
Tx = P(x)N
∴ First frequency term:
T1 = P(x = 1) N = 16
i.e., 3C1 P1 q3-1 N = 16
3P q2 N = 16 …………(1)
Similarity second frequency terms: T2 = P(x = 2) N = 15
i.e., 3C2 P2 q3-2 N = 15
3P2qN = 15 ………… (2)
(2) → (1)
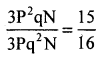
P = 0.9375 q;
∵ q = 1 – P.
P = (l-P) 0.9375;
P = 09375 – 0.9375 P
P + 0.9375 P = 0.9375
1.9375 P = 0.9375
\(\mathrm{P}=\frac{0.9375}{1.9375}=0.4838\)
Poisson Distribution
Question 1.
The chance of contracting tuberculosis bya a workers in a cement factory is \(\frac{1}{50}\). Find the probability that out of 10 workers in the factory, 4 will get the disease.
Answer: Let JC be the number of workers contracting the disease is a Binomial Variate with the parameter
n = 10 and P = P (Worker contracting disease) = \(\frac{1}{50}\) = 0.02
Here P is very small (i.e., p → 0) and n is comparatively large (n → ∞) and np = 10 x 0.02 = 0.2 = λ which leads to poisson distribution. With mean λ = 0.2.
The p.m.f is –

Question 2.
On an average a box contains 3 defective items. Find the probability that a randomly selected box has:
(a) One defective item only
(b) Atleast 2 defective items.
Answer:
Let x be the number of defective items is a Poisson variate with the parameter (mean) X = 3.
The p.m.f is –

(a) p (one defective item) = p(x = 1) =\(\frac{e^{-3} 3^{1}}{1 !}\) = 0.04978 x 3 = 0.1494
(b) p (atleast 2 defective items)
= p(x ≥ 2) = 1 – p(<2) = 1 – {p(x = 0) + p(x = 1)}
[Note: Here in poisson distribution Maximum limit is ∞]
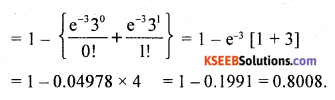
Question 3.
3% of the bulbs manufactured by a company is found be defective. Find the probability that a box of 50 bulbs contains (a) exactly 4 (b) 2 or more defective bulbs.
Answer:
Let x be the number of defective bulbs is a Binomial variate with the parameters n = 50, p = p (defective bulbs) = 3% = 0.03.
Here n is large, p is very small and np = X = 50 x 0.03 = 1.5 which leads to poisson distribution with the parameter λ = 1.5.
The p.m.f is –
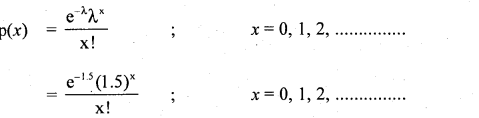
(a) p (exactly 4 defective bulbs)
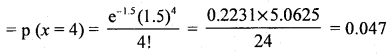
(b) p (2 or more defective bulbs)
= p(x ≥ 2) = 1 – p(x < 2)
= 1 – {p(x = 0) + p(x = 1)}
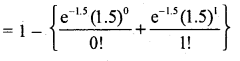
= 1 – e-1.5 (1 + 1.5)= 1 – 0.2231 x 2.5
= 1 – 0.5578 = 0.4422
![]()
Question 4.
2% of the fuses manufactured by a firm are expected to be defective. Find the probability that a box containing 200 fuses contain (a) defective fuses (b) 2 or more defective fuses. –
Answer:
Let x be the number of defective fuses is a Binomial variate with parameters n = 200, p = p (defective fuse) = 2% = 0.02.
Here n is large, p is very small and np = 200 x 0.02 = 4 which leads to poisson distribution.
The p.m.f is –

(a) p (box contains defective fuses)
= p(x ≥ l) = 1-p(x< 1) = 1-p (x = 0)
\(=1-\frac{\mathrm{e}^{-4} 4^{0}}{0 !}\)
= 1 – 01832 = 0.9816
(b) p (2 or more defective fuses)
= p(x ≥ 2)
= 1 – p(x < 2)
= 1 – {p(x = 0) + p(x = 1)}
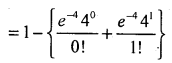
= 1 – e-4 (1 +4)
= 1 – (0.0183 × 5)
= 1 – 0.0915 p(x ≥ 2) = 0.9085.
Question 5.
The probability that a razor blade manufactured by a firm is defect is \(\frac{1}{500}\) Blades are supplied in packets of 5 each. In a lot of 10000 packets. How many packets would (a) be free of defective (b) contain exactly one defective blade?
Answer:
Let x be the number of defective blades is a Binomial variate with parameters n = 5,
p = p (defective blades) = \(\frac{1}{50}\) = 0.002
Here n is large p is very small and np = 1 = 5 x 0.002 = 0.01, which leads to poisson distribution.
The p.m.f. is –

(a) p (free of defectives)
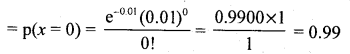
∴The number of packets containing no defective blades = p(x = 0) x N
= 0.99 × 10000 =9900
(b) p (exactly one defective blade)
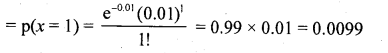
∴ The number of packets containing exactly 1 defective blade = p(x = 1) x N
= 0.0099 x 10000 = 99
Quesiton 6.
In a textbook, on an average 0.2 mistakes per page is found. If there are 565 pages in that book , in how many pages, there will be (a) exactly 2 (b) less than or equal to 1 mistakes.
Answer:
Let ‘x’ be the number of mistakes per page is a poisson variable with the parameter, mean, λ = 0.2
The p.m.f. is –
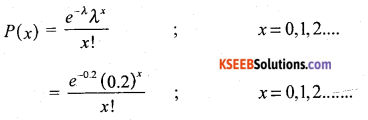
(a) P (exactly 2 mistakes per page)
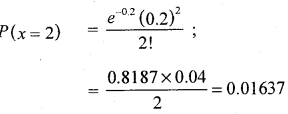
Number of pages with exactly 2 mistakes per page
= P(x = 2) × 565 = 9.25 pages
(b) p (less than or equal to 1 mistakes per page)
= P(x ≤ 1) = P(x = 0) + P(x = l)
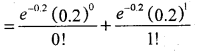
= e-0.2 (1 + 0.2)
= 0.8187 × 1.2 = 0.9824
Number of pages with less than or equal to 1 mistakes per page
= (x ≤ 1) x 565 = 555.08 pages
Question 7.
Fit a Poisson distribution and obtain the theoretical frequencies :

Answer:
If X is a poisson variate the parameter X is obtained as :
We know that mean \(\lambda=\frac{\sum f x}{N}\)
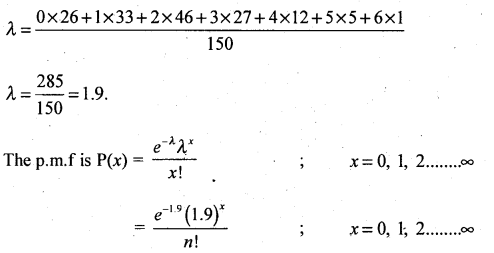
Theoretical frequency : Tx = P(X)N.
To = P (x = 0) × 150
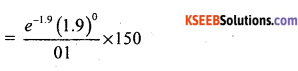
T0 = 0.1496 × 150 = 22.44
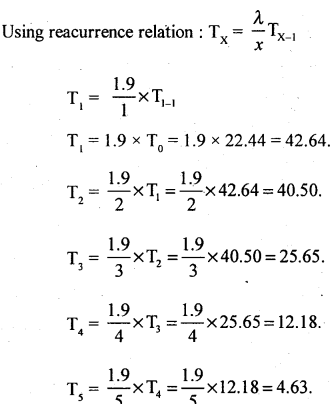
T6 or more = N – [T0 + T1 + T2 + T3; + T4 + T5]
= 150 – [22.44 + 42.64 + 40.50 + 25.65 + 12.18 + 4.63]
T6 or more= 150 – 148.01 = 1.99.
The distribution of observed and theoretical frequency is : (Approximated)

Normal Distribution
Question 1.
Define a Standard Normal variate and mention important properties of normal curve. Answer: A normal variate with mean µ = 0 and standard deviation σ = 1 is called SNV. It is denoted by Z.
The p.d.f. of SNV is-
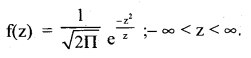
Properties:
- The curve is bell shaped; here X̄ = M = z.
- The curve is symmetric about mean i.e. the distribution is non skewed; β1 = 0.
- The area under the normal curve = 1
- For the distribution : standard deviation = σ
Quartile deviation = \(\frac{2}{3}\) σ
Mean deviation = \(\frac{2}{3}\) σ - The distribution is mesokurtic ; β2 = 3.s
![]()
Question 2.
The mean of a Normal distribution is 120 and SD is 40. Find the probability that the value of the variable selected at random will be: (/) over 150 (//) between 60 and 90,
Answer:
Let x be the Normal variable with mean µ = 120 and cr = 40 then standar normal variate z = x-p O
\frac{\mathrm{x}-\mu}{\sigma}

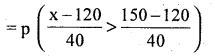
= p (z > 0.75)
= Area from (0.75) to ∞.
= Area from 0 to ∞ – Area from 0 to (0.75)
= 0.5 – 0.2734 = 0.2266
(b) p (variable is between 60 and 200) .
= p (60 < x < 200)
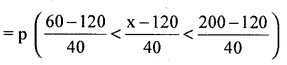
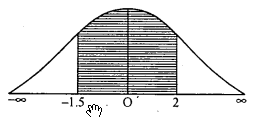
= p(-1.5 < z < 2)
= Area from (-1.5) to 2.
= Area from 0 to (-1.5) + Area from 0 to 2.
= 0.4332 + 0.4772 = 0.9104
Question 3.
x is a normal variate with mean 60 and standard deviation on 12.
Find: (a) p (x ≥78) (b) p (66 ≤ x ≤ 78)
Answer:
Let x be the normal variable with parameters µ = 60 and σ = 12, then SNV
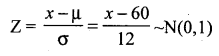
(a) p(x ≥ 66) =
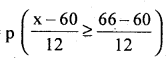
= p(z ≥ 0.5)
= Area from 0.5 to ∞
= Area from 0 to ∞ – Area from 0 to 0.5
= 0.5 – 0.1915 = 0.3085
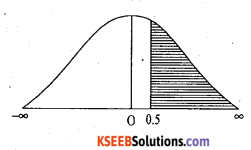
(b)
![]()
= p (66 ≤ x ≤ 78)
= p (0.5<z< 1.5)
= Area from 0.5 to 1.5
= Area from 0 to 1.5 – Area from 0 to 0.5
= 0.4332 – 0.1915 = 0.2417.
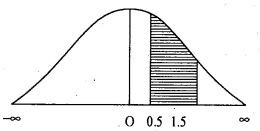
Question 4.
Given a Normally distributed vax-iablexwith mean 18 and SD 2.5.
Find: (a) p(16 < x < 22) (b) (19< x < 23)
Answer:
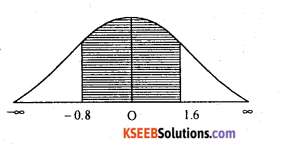
Let x be normal variate with the parameters µ = 18, σ = 2.5 then SNV
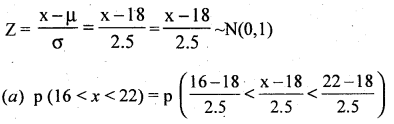
= p(-0.8 < z < 1.6)
= Area from (-0.8) to 1,6
= Area from 0 to (-0.8) + Area from Oto 1.6
= 0.2881 + 0.4452
= 0.7333
(b) p(19<x<23)=
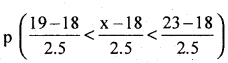
= p (0.4 < 1 < 2)
= Area from (0.4) to 2.
= Area from 0 to 2 – Area from 0 to 0.4
=0.4712 – 01554
= 0.3218
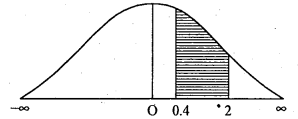
Question 5.
The weight of 100 students are Normally diatributed with mean 50 kg and standard deviation 5 kg. Find the number of students with Weight : (a) below 40 kg (b) between 40 and 55 kg.
Answer:
Let x be the weight of students is a Normal variable with paramctcrs µ = 50 kg and S.D. = σ = 5kg,thenSNV.
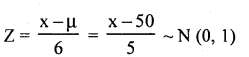
(a) p (weight below 40 kg) p (x < 40)
= 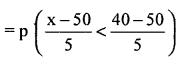
= p(Z < -2)
= Area from (-2) to (-∞)
= Area from O to (-∞) Area from O to (-2)
= 0.5 – 0.4772 (from table)
= 0,0228
The number of students with below 40 kg = p (x < 40) x N
= 0.0228 x 100
= 2.28 = 2 students
(b) p (weight is between 40 and 55 kg)
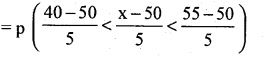
= p (-2 < z < 1)
= Area from (-2) to 1
= Area from 0 to (-2) + Area from 0 to 1
= 0.4772 + 0.3413
= 0.8185
∴ The number of students with weight between 40 and 55 kg.
= p(40 < x < 55) × N
= 0.8185 × 100
= 81.85 ≅ 82 students.
![]()
Question 6.
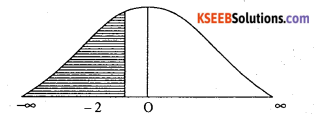
Monthly income of employees follows normal distribution with mean Rs. 8,000 and standard deviation Rs.600. Find the probability that a randomly selected employee’s income
(a) is less than Rs. 6,500
(b) lies between Rs.8,720 and Rs. 9,200.
Answer: Let x be the monthly income of employees is a normal variate with the parameters mean.
µ = 8000 and S.D.σ = 600 ,
then S.N.V. .
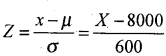
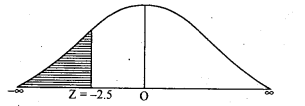
(a) P( income is less than Rs. 6,500)
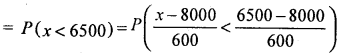
= P(z < – 2.5)
= Area from 0 to (-∞) – Area from 0 to (-2.5)
= 0.5 – 0.4938
P(x < 6500) = 0.0062
(b) P(Income lies between Rs.8,720 and Rs. 9,200)
= P (8720 <x< 9200)
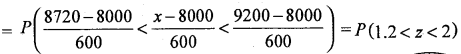
= Area from 0 to 2 – area from 0 to 1.2
P(8720 < x < 9200) = 0.4772 – 0.3 849 = 0.0923
Question 7.
The marks scored by the students of a class follow Normal distribution with mean 80 and SD.5. Find the probability that a student selected at random from the class scored,
(a) more than 90 marks
(b) between 70 and 85 marks.
Answer:
Let ‘x’ be marks scored by the student is a Normal Variate with the parameters, µ = 80, σ = 5, then S.N.V. is
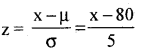
(a) P(marks scored more than 90)
= P (x > 90)
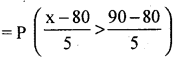
P(z > 2)
Area from 2 to ∞
=Arcafrom 0 to ∞ – Area from 0 to 2
P(x > 90) 0.5 – 0.4772 = 0.0228
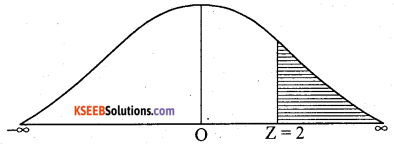
(b) P (marks score between 70 and 85)
P(70 < x < 85)
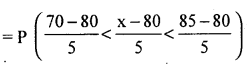
P(-2 < Z < 1)
Area from (-2) to 1
= Area from 0 to (-2) + Area from 0 to 1
= 0.4772 + 0.3413 = 0.8 185
![]()
Question 8.
The weights of 1000 Punjabi youths are normally distributed with mean 50 kgs and S.D. 5 kgs. Find the number of Punjabi youths with weight in between 45 kgs and 55 kgs.
Answer:
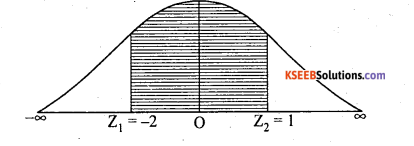
Let X be the weights of youths is a nomal variate with mean µ = 50 and S.D σ = 5, then S.N.V.
![]()
Number of youths with weight between 45 and 55 kgs
= p(45 < x < 55) x 1000
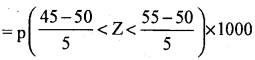
= p(-1 < Z < 1) × 1000 = Area from (-1) to 1 × 1000
2(Areafrom 0 to 1) × 1000= 2 × 0.3413 × 1000 = 0.6826 × 1000.
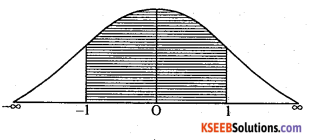
Hypergeometric Distribution
Question 1.
A bag contains 18 balls of which 13 are white and 5 are black in colour. Arandom sample of 5 balls are selected. Find (i) Expected number of black balls drawn
(ii) the probability that 2 are black balls
(iii) all are black balls.
Answer:
Let x denote the number of black balls drawn is a Hyper geometric variate with parameters a = 5, b = 13 and n = 3 The p.m.f is:-

(i) Expected number of black balls drawn = E(x)
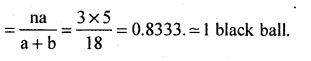
(ii) P(2 are black balls) = P(x = 2)
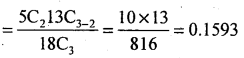
(iii) P(all are black balls) = P(x = 3)
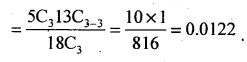
Question 2.
In a office, 20 members are vegetarians and 12 members are non – vegetarian A commi-tee of 6 members are formed. Find the probability the among the members
(i) resctly 2 are vegetarians and
(ii) at least 2 are vegetariAnswer:
Answer:
Let x denote the number of vegetarians in a commitee is a Hyper geometric variate with parameters a = 20, b = 12 and n = 6. then the p.m.t. is:-

(i) P(exactly 2 are vegatarians)
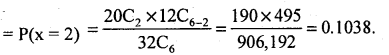
(ii) P (atleast 2 are vegetarians)
= P(n ≥ 2) = 1 – P(x < 2)
= 1 – [P(n = 0) + P(x = 1)]
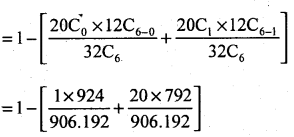
= 1 – (0.00102 + 0.01748
= 1 – 0.0185
P(x ≥ 2) =0.9815.
Question 3.
There are 10 boys and 5 girls in a class. 4 stadents are randly selected. Find the probability that among the selected students
(i) have no girls
(ii) atleast two girls.
Answer:
Let x denote the number of girls in the selection is a Hyper geometric variate with the parametex a = 5, b = 10, n = 4. Then the p.m.f. is:-

(i) P(selecting no girls)
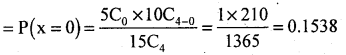
(ii) P(Selecting atleast 2 girls)
= P(x > 2) = P(x = 2) + P(x = 3) + P(x = 4) OR
= 1 – P(x < 2)= 1 – [P(x = 0) + P(x= 1)]
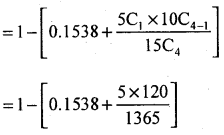
= 1 – 0.5934
P(x ≥ 2) = 0.4066.
![]()
Question 4.
A box has 12 Red and 8 pink marbles. 5 marbles are randomly picked. Find mean, variance and S.D. of Hyper geometric distribution of pink marbles drawn.
Answer:
Here x ~ pink marbles.
a = 8, b = 12, n = 5, Here a + b = 20

Question 5.
A bag has 8 white and 5 yellow balls. 3 balls are selected at random. Let x denote the number of white balls drawn and let y denote the number of yellow balls drawn.
(i) Find the expected number of white balls in the selection. Also find variance.
(ii) Find the expected number of yellow balls in the selection.
(iii) Find the var(x) and var (y).
Answer:
x ~ no. of white balls.
a = 8, b = 5, a + b = s, n = 3 a + b = 1
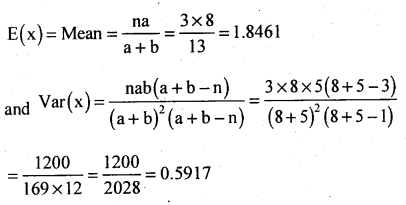
(i) x ~ No. of yellow balls drawn,
a – 5, b = 8, a + b =s, n = 3
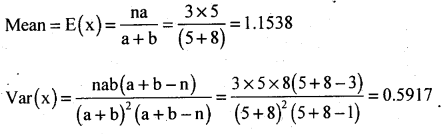
2nd PUC Statistics Theoretical Distribution Ten Marks Questions and Answers
Question 1.
5 fair coins are tossed 128 times. Write down the theoritical frequencies of the distribution of heads.
Answer: Let x be the number of heads obtained is a Binomial variate with n = 5, P = Vi (coin is fair).
q = 1/2
The p.m.f is
p (x) =ncx px qn – x; x = 0,1,2, …… n
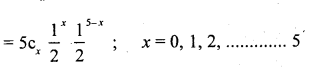
Theoretical frequency = Tx = p [x] x N.
∴ T0 = p[x = 0] x 128
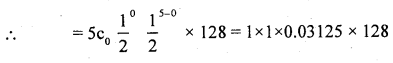
∴ T0 =4
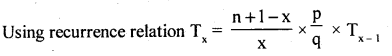
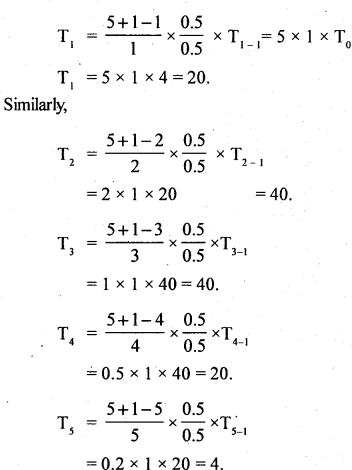
∴ The theoritical frequency distribution of numbers heads is –

[Note: Since the coin unbiased t le frequncies are symmetrically distributee •]
Question 2.
7 fair coins are tossed 384 times. Find the expected frequencies of the number of heads obtained.
Answer:
Let x be the number of heads obtained is a binomial variate with the parameters n = 7 and N = 384. Since the coin is fair.
Therefore P = \(\frac { 1 }{ 2 }\) and q = \(\frac { 1 }{ 2 }\)
The p.m.f is : P(x) = ncx px qn – x; x = 0,1,2, …… n
7cx0.5x0.57 – x; x = 0,1,2, …… 7
Theoretical / expected frequency : Tx = P(x) × N
To = P(x = 0) x 384
= 7C0(0.5)0(0.5)7-0 × 384
T0 = 3
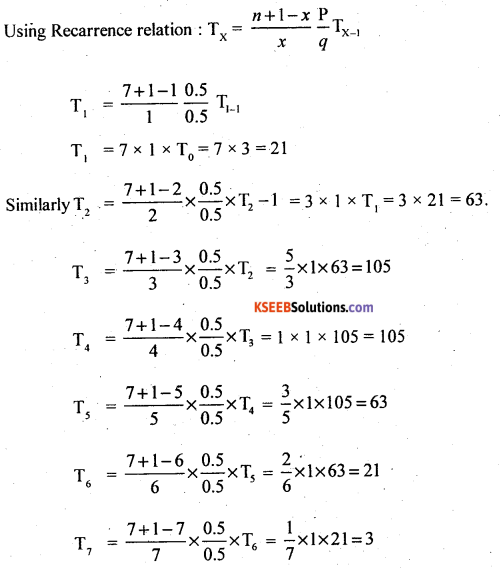
The expected frequencies of the number of distribution of heads is:

Question 3.
Fit a binomial distribution for the following data and obtain the expected frequencies.

Answer:
Here x is the number of defectives is a Binomial variate with n = 5. The parameter p can be obtained as below.
We know that mean = X̄ = np = \frac{\Sigma \mathrm{fx}}{\mathrm{N}}=\frac{100}{50} = 2 [ from the frequency distribution]
i.e 5p = 2. ∴ p = 0.4 ∴ q = 0.6
The p.m.f is –
P(x) = ncx px qn-x; x = 0,1,2, …… n
= 5cx (0.4)x (0.6)5-x ; x = 0,1,2, …….. 5
Theoretical/Expected frequency = Tx= p[x] × N.
∴ Tx = p[x = 0] x 50
= 5C0 (0.4)0 (0.6)5-0 × 50 = 1 × 1 × 0.07776 × 50 T0 =3.88
T0 = 3.88

The fitted observed and theoritical frequency distribution is: (Approximated)

Question 4.
The following table gives the number of deaths per day in a hospital for 400 days. Fit a poisson distribution and obtain the theoritical frequencies for the data.
Answer:
Let x be the number of deaths per day is a poisson variate, the parameter λ can be obtained as:
Let f be the number of days, then we know that

Theoretical frequncy = Tx = p(x) × N.
∴ T0 = p(x = 0) × 400.
= \(\frac{\mathrm{e}^{-16}(1.6)^{0}}{0 !}\) × 400 = 0.2019 × 400= 80.76

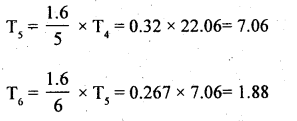
T(7 or more) = N – [ T0 + T1 + T2 +…. + T6 ]
= 400 – [80.76 + 129.22.103.38 + 55.14 + 22.06 + 7.06 + 1.88]
= 400 – 399.5
= 0.5
∴ The fitted observed and theoretical frequency distribution is:

![]()
Question 5.
Fit a poisson distribution to the following data and hence find theoretical frequencies:

Answer:
Let x be poisson variate, then the paramter λ can be obtained as :-
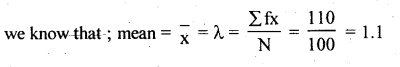
The p.m.f is

The theoritical frequency Tx = p(x) × N
∴ T0 = p(x = 0) × 100
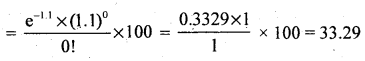
∴ T0 = 33.29
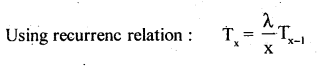

∴ The fitted observed and theoretical frequency distribution is Approx

Question 6.
If the height of 500 soldiers are found to be normally distributed with mean 70” and standard deviation 12”, find the number of soldiers whose heights are (/) below 56″ (JI) above 73″ («7) between 66″ and 73″.
Answer:
Let x be the height of soldiers is a Normal variate with meari μ = 70″ and SD = σ = 12″, then
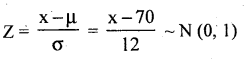
(i) p (height is below 56″) = p(x < 56)
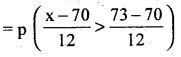
= p (Z ← 1.17)
= Area from (-1.17) to (-∞) – Area from 0 to (-1.17)
= 0.5-0.3790
= 0.1210
∴ The number of soldiers whose height is below 56″
= p (x < 56) × N
= 0.1210 × 500
= 60.5 ≅ 61 soldiers 19
(ii) p (height is above 73″) = p(x > 73)
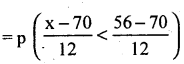
= p (Z > 0.25)
= Area from 0.25 to ∞.
= Area from 0 to ∞ – Area from 0 to 0.25
= 0.5 – 0.0987 = 0.4013.
∴The number of soldiers whose height is above 73″
= p (x > 73) × N
=0.4013 × 500
= 200.65 ≅ 201 soldiers.
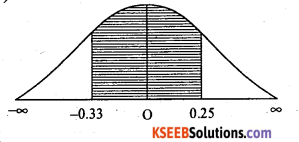
(iii) p (height is between 66″ and 73″) = p(66 < x < 73)
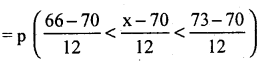
p(-0.33 < Z < 0.25)
= Area from (0.33) to (0.25)
= Area from 0 to 0 to (-0.33) – Area from 0 to (0.25)
= 0.1293 + 0.0987
p (66 < x < 73) = 0.228.
∴ The number of students whose height is between 66″ and 73″
= p (66 < x < 73)× N
= 0.228 × 500
= 114 soldiers.
Question 7.
Heights of 2000 soldiers are normally distributed with mean 160 cms and standard deviation 5 cms. Find the number of soldiers with height.
(i) less than 155 cms
(ii) between 160 cms and 165 cms
(iii) more than 170 cms.
Answer:
Let X be the heights of soldiers is a normal variate with the parameters mean m = 160 and S.D. s = 5, then S.N.V,
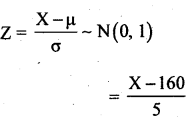
(i) Numbcr of soldiers with height less than 155 ems.
=P(x < 55) × 2o00
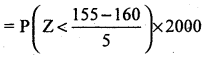
=P(Z < -1) × 2000
= Area from (-1) to (-∞) × 2000
= Area from 0 to (-∞) – Area from 0 to (-1) × 2000
=0.5 – 0.3413 – 0.1587 × 2000
=317.4
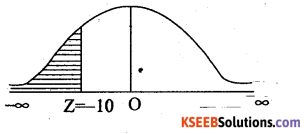
(ii) P(height between 160 and 165 cms)
= P(160 < X < 165)
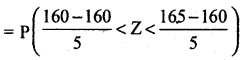
=P(0 < Z < 1)
= Area between 0 to 1
= Areafrom 0 to 1
= 0.3413
Number of soldeirs with height between 160 & 165 cms.
= 0.3413 × 2000= 682.6
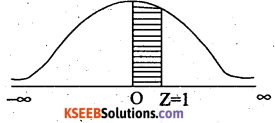
(iii) P(hcight more than 170 ems)
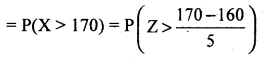
= P(Z> 2)
= Area from 2 to ∞
=Area from 0 to ∞ – Areafrom 0 to 2
= 0.5 – 0.4772
= 0.0228
Number of soldiers whose height is more than 170 ems = 0.0228 × 2000 = 45.6.
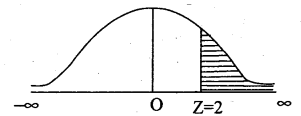
Question 8.
The weekly wages of 1000 workmen are normally distrbuted around a mean of Rs.70 and with standard deviation of Rs.5. Estimate the number of workers whose weekly wages wil be: (i) Between Rs. 69 and Rs. 72, (ii) more than Rs.75.
Answer:
Let x be the weekly wages is a normal variate with mean µ= 70 and SD σ = 51, given
N = 1000. then SNV,
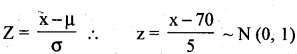
(i) p (wage is between Rs. 69 and Rs. 72)
= p (69 < x < 72)
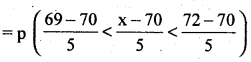
= p (-0.2 < Z < 0.4)
= Area from (0.2) to (0.4)
= Area from 0 to (-0.2) + Area from 0 to (0.4)
= 0.0793 + 0.1554
= 0.2347
∴ The number of workers whose weekly wages is between Rs. 69 and Rs. 72
= p (69 < x < 72) × N
= 0.2347 × 1000 = 234.7 ~ 235 workers
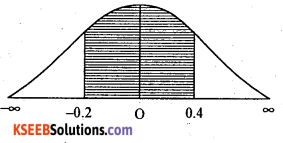
(ii) p (wage is more than Rs. 75)
= p (x >75)
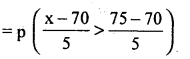
= p(z > 1)
= Area from 0 to ∞ – Area from 0 to 1
= 0.5-0.3413 = 0.1587
∴ The number of workers whose weekly wage is more than Rs. 75
= p(x >75) × N = 0.1587 × 1000
= 158.7 ≅ 159 workers.
Question 9.
The mean and standard deviation of marks obtained by the candidates in a competitive examination are 50 and 15 respectively. If 1200 candidates appear for the examination find:
(i) The number of candidates who are expected to score more than 70 marks.
(ii) The expected number of candidates who score between 58 and 80 marks:
Answer:
Let x be the marks obtained in an examination is a normal variate with the parameters mean
µ = 50 and SD = σ = 15. Given N = 1200 then SNV,
![]()
(i) p (marks more than 70)
= p(x> 70)
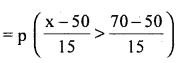
= p (z > 1.33)
= Area from 1.33 to ∞.
= Area from 0 to ∞ – Area from 0 to (1.33)
= 0.5 – 0.4082
∴ The number of candidates who are expected to score more than 70 marks
= p (x > 70) × N
= 0.0918 × 1200
= 110.16 ~ 110 candidates.
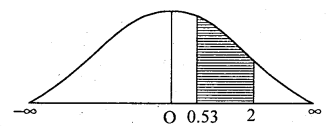
(ii) p (marks between 58 and 50)
p(58 < x < 80)
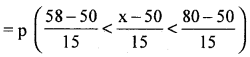
= p(0.53 < Z Z < 2)
= Area from O to 2
Area from 0 to 2 – Area from Oto 0.53
= 0.4772 – 0.2019
= 0.2753
= 0.2753
∴ Expected number of candidates who score between 58 and 80 marks
= p (58 < x < 80) × N.
= 0.2753 × 1200
= 330.36 ~ 330 candidates.