Students can Download 2nd PUC Statistics Previous Year Question Paper March 2015, Karnataka 2nd PUC Statistics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Previous Year Question Paper March 2015
Time: 3 Hrs 15 Min
Max. Marks: 100
Section-A
I. Answer any TEN of the following questions : (10 × 1=10)
Question 1.
Define expectation of life.
Answer:
It is the average number of years a person aged x can expected to live under the prevailing mortalite conditions.
Question 2.
If the general price level goes up by 80% between 2000 and 2012. What is the index number for 2012 with base 2000?
Answer:
Index number for 2012 = 180
Question 3.
Name the index number which satisfies circular test.
Answer:
Kelly’s method and simple geometric mean of price relatives method.
Question 4.
Which index is used for the measurement of seasonal variation?
Answer:
Seasonal Indices method.
![]()
Question 5.
If p = \(\frac { 1 }{ 4 }\) for a Bernoulli distribution, write down the p.m.f.
Answer:
p.m.f is P(x) = \(\left(\frac{1}{4}\right)^{x}\left(1-\frac{1}{4}\right)^{1-x}\) : x = 0,1
= (0.25)x (0.75)1-x: x = 0 , 1
Question 6.
What is the probability that a normal variate takes a value greater than its mean?
Answer:
0.5
Question 7.
Define sampling distribution of a statistic.
Answer:
It is distribution of the values of a statistic for different samples by same size.
Question 8.
What is power of a test?
Answer:
It is the probability rejecting to, when it is not true : (1- β) i Here β = P (Type II error)
Question 9.
If p = 0.02 and n = 64 then find SE (p).
Answer:

Here Qo = 1 – Po = 1 – 0.02 = 0.98
Question 10.
Define acceptance sampling.
Answer:
It is the process of inspecting a random sample of goods and deciding whether to accept the entire lot based on the results.
Question 11.
What is meant by lead time?
Answer:
It is the time gap between the placing of order and arrival of goods at the Inverotory (T).
Question 12.
When a T.P. balanced?
Answer:
When Σai -Availabilities = Σbj – Requirements then the T-P is said to be balanced.
Section – B
II. Answer any TEN of the following questions : (10 × 2=20)
Question 13.
In a locality 10,000 live births occnred. The number of infant deaths was 500. Calculate infant mortality rate.
Answer:
![]()
Question 14.
State two characteristics of index numbers.
Answer:
- Index numbers are specialised averages.
- Index numbers are expressed in ratios but for better comparision expressed in percentages.
Question 15.
Quantity index number of current year is 250. If the number of units produced in the current year is 120 then find the number of units produced in the base year.
Answer:

![]()
Question 16.
Diagrammatically represent ‘Business Cycle’ with stages
Answer:

Question 17.
Define ‘Interpolation’ and ‘Extrapolation’.
Answer:
‘Interpolation’ is the technique of estimating a value of the dependent variable (y) for any intermediate value of the independent variables (x) ‘Extrapolation’ is the technique of estimating the value of dependent variable (y) for any value of the independent variable (x) which is outside the range of the given series.
Question 18.
For a hypergeometric distribution the parameters are a = 7, b = 5 and n = 8. Find the variance.
Answer:

19.
If z1 and z2 are two independent SNVs, then name the distribution of z12, + z22 and find its mean.
Answer:
(z12, + z22,) ~ χ2(2) d.f. ie; is a chi-square distribution with n = 2 degress of freedom mean = n = 2.
20.
Write two applications of t-test.
Answer:
Under small sample tests t-distribution is used
- to test whether the population has the given mean,
- to test whether two population means are equal (=/>/<)
21.
Mention two conditions for applicability of Chi-square test of goodness of fit.
Answer:
- Total number of frequency N should be large.
- Theoretical/Expected frequency each Ei should be 5 or more (Ei ≥ 5) if any one is below it should be pooled with the adjacent frequencies (untill together 5 or more)
- If any one of the parameter is estimated from the data for each such estimation one degrees of freedom should be lessened.
22.
In a floor mat manufacturing company, the average number of defects per square meter of floor mat is known to be 4. Find the upper control limit for the number of defects.
Ans.
Given: λ1 =4. The upper control limit for C – chart: UCL = \(\lambda^{1}+3 \sqrt{\lambda^{1}}=4+3 \sqrt{4}=10\)
23.
Under what conditions is E.O.Q. model with shortage applicable.
Answer:
- Uniform demand
- Production is Instantaneous
- Lead time is Zero
- Shortages are allowed.
24.
From the following T.P. test whether the solution is non-degenerate:

Answer:
Here no. positive allocations = 4; m + n – 1 = No. of rows + No. of columns -1 = 3 + 3 -1 = 5
Here no. of allocations < (m + n – 1) the solution is degenerate / not a non-degenerate.
![]()
Section – C
III. Answer any EIGHT of the following questions : (8 x 5 = 40)
)Question 25.
Compute the Gross reproduction rate from the following data :

Answer:



W. S. F. R (15-19) = \(\frac { 19 }{ 1658 }\) × 100 = 11.459
Similarly for remaing age groups W.S.F.R can be computed. Here i = 5
G. R. R. = 5 × 200.272 = 1001.36 Female births / 1000 women of (15-49) years.
Question 26.
Briefly explain TRT and FRT.
Answer:
TRT: Time reversal test requires that the index number computed backward (P10) should be reciprocal of the index number computed time forward (P10)
i.e., P10 = \(\frac{1}{\mathrm{P}_{01}}\); Exccept the factor 100.
FRT: Factor reversal test requires that the product of price and quantity index numbers both computed time forward is equal to the total change in the value.

Question 27.
compute the cost of living index number by using the following data

Answer:
Weights (W) are given , so use family budged method to compute cost of living imdex number C.P.I./IO = \(\frac{\Sigma \mathrm{PW}}{\Sigma \mathrm{W}}\) ; Where, p = \(\frac{P_{1}}{P_{0}} \times 100\) the price relative and W – Weghts

I01 = \(\frac { 3560 }{ 27 }\) = 131.85 ≅ 132
There is net in crease of cost of living by 32% (132-100) in the current year as compared to base year.
Question 28.
Compute trend values by using 4-yearly moving averages method:
| Year | Sales (000) |
| 2000 | 70 |
| 2001 | 85 |
| 2002 | 75 |
| 2003 | 70 |
| 2004 | 70 |
| 2005 | 65 |
| 2006 | 60 |
| 2007 | 55 |
| 2008 | 60 |
| 2009 | 75 |
Answer:
Let x and y be the year and sales.

From the trend values the sales shows down word trend.
![]()
Question 29.
Interpolate and extrapolate the production for the year 2006 and 2010 for the following data:

Answer:
Let x and y be the year and production.

The number of known values of y; n = 4 and so, the normal expansion (y – 1)4= 0.
y4 – 4y3 + 6y2 – 4y1 + y0 = 0
26 – 4(15) + 6 (10) – 4y1 + 5 = 0
26 – 60 + 60 – 4y1 + 5 = 0
31 – 4y1 = 0; ∴ y1= \(\frac { 31 }{ 4 }\) = 7.75 .
So, the production for the year 20.6 = 7.75
For the entropolation for y5 consider the equation 1, increase the suffixes of y by 1, we get
y5 – 4y4 + 6y3 – 4y2 + y1= 0
y5 – 4(26)+ 6 (15) – 4(10) + 7.75 = 0
y5 – 104 + 90-40 + 7.75 = 0
y5 – 46.25 = 0; ∴ y5 = 46.25
∴ The production for the year 2010 = 46.25 tons.
Question 30.
In a certain school 40% of the students have opted for first language Kannada. Assuming 20 teachers take a sample of 4 students each, how many teachers will report that 2 or 3 students opted for first language Kannada?
Answer:
Let x be the numbers students opted first language kannada is a Binomnal variate with the parameters.
n = 4; P = 40% = 0.4; q = 1 – p = 0.6 and N = 20.
The p. m. f. is P(x) = nCxPx qn-x = 1 – p = 0.6 and N = 20
P(x) = 4Cx(0.4)x (0.6)4 – x ; x = 0,1,2,3,4
Number of teachers will report 2 or more students opted for first language kannada
= P(x = 2) + P(x = 3) = 4C2(0.4)2 (0.6)4 – 2 + 4C3(0.4)3(0.6)4-3
= 0.3456 + 0.1536 = 0.4992 × 20 = 9.98
Question 31.
In a text book, on an average 0.3 mistakes per page is found. If there are 500 pages in that text book, in how many pages will there be at the most two mistakes?
Answer:
Let x be the numbers of print mistakes pef page is a poisson variate with the parameter λ = 0.3, then the p.m.f. is :

Number of pages having at the most 2 mistakes
= P(x ≥ 2)N = 1 – P(x < 2)N = 1 – [P(x = 0) + P(x = 1)

= 1 – e-0.3(1 + 0.3) = [1 – 0.7048 × 1.3] = 1 – 0.9630
= 0.037 × 500 = 18.5 symbol undi 19 pages
Question 32.
A random sample of 400 tins of Vanaspathi has mean weight 4.96 kg and S.D. 0.4 kg. Test at 1% L. O. S. that the average weight of tins of Vanaspathi is less than 5 kg.
Answer:
Given : n = 400; x̄ = 4.96; S = 0.4, α = 1% µ = 5
H0 : Mean weight of tens is 5 kg (Ho: p = 5kg) –
H1 : Mean weight of tens is less than 5kg
(H1 : µ < 5 kg) { Lower tail test; -K}

under H0 the test statistic is :-

Zcal = -2
At α = 1% the lower tail critical value – K = -2.33
Here Zcal lies in A.R .
∴ H0 is Accepted
Conclusion: Mean weight of tins is 5kg.
Question 33.
Following is the data regarding I.Q. of five students before and after performing yoga.

Is training effective? (Use 5% L.O.S.)
Answer:
H0 : Mean I.Q. be for and after Yoga is same (H0: µ1 = µ2)
H1 : Mean I.Q. has increased after Yoga (H, : µ1 < µ2) {Upper tail test + K}
Under H0, the paired t-test statistic is

let x and y be I. Q. before and after yoga.


At ∝ = 5% for (q-1) = 5-1 = 4.d.f.
The lower tail critical value -K = -2.13
Here tcal lies in R. R.
∴ H0 is rejected and H1 is accepted
Condusion : I. Q. has improved after yoga

![]()
Question 34.
For the following data find out the control limits for X̄ – chart. (Given A2 = 0.577)

Answer:
Standands not known; for X̄ chart we need

The control limits for X̿ – chart K = 6
C.L = X̿ = 49.5
L.C.L= X̿ – A2R̄
= 49.5 – 0.577 × 10.16
= 43.63
U.C.L =X̿ + A2R̄
= 49.5 + 0.577 × 10.16
= 55.36
Question 35.
Graphically solve the given L.P.P.
Maximize Z = 12x + 40y
S.t.
3.v + 3y ≤ 12
6x + 3y ≤ 18 and x, y ≥ 0.
Answer:
Consider the constraints as equalities and find co-ordinates
3x + 3y = 12;
Put x = 0; We get y = 4; (0,4)
Put y = 0; We get x = 4; (4,0)
6x + 3y = 18;
Put x = 0; We get y = 6; (0,6)
Puty = We get n = 3; (3,0)
and x = 0; y = o

From the graph the feasible region exists at the comer points 0(0,0), A (0,4), B(2,2), C(3,0)
Determination of optimun value of objective function.

From the above table. Objective function ‘Z’ maximizes at the comer point A (0,4) The suggested optimun solution for the L.P.P. is x = 0, y = 4 and z A = 160
OR
(For Blind Students Only)
Write down the steps in the graphical method of solving LPP.
Answer:
Finding a solution to a L.P.P. by graphical method.
- Consider the constraints as equalities.
- Find the co-ordinates for each constraints.
- Draw the graph and represent by straight line.
- Identify the feasible region, which satisfies the non-negativity restrictions and constraints . simultaneously.
- Locate the comer points of the feasible region.
- Find the value of the objective function each of the corner points of the feasible region.
- get the optimom value and suggest the solution for the L.P.P.
Question 36.
The following are the maintenance and depreciation costs per year of a vehicle whose purchase price is Rs. 50,000. –

When should the vehicle be replaced?
Answer:
Given Depreciation cast: (P-sn) and maintenance cost Ci and P = 50,000.
The Vehicle is suggested to replace when its Annual average maintenance cost is A(n) is least/ minimum over a period.

Here T = (P-Sn) + ΣCi
From the above table the Annual average maintenance cast A(n) is least for the year n = 6 and so, the vehicle should replace after the use of 6 years, and A(6) = Rs. 17083.33
![]()
Section – D
IV. Answer any TWO of the following questions : (2 x 10 = 20)
Question 37.
For the following two towns compute standardized death rates and comment:

Answer:

be the standardised death rates of town A and B and Ps. The standard population, A and B be their respective Age specific death rates.

![]()
ASDR (0-20) = \(\frac { 128 }{ 8000 }\) × 1000 = 18
SDR (A) = \(\frac { 19,05,000 }{ 1,00,000 }\)

ASDR (0 – 20) = \(\frac { 72 }{ 4000 }\) × 1000 = 18
SDR (B) = \(\frac { 16,75,000 }{ 1,00,000 }\) = 16.75
Here S.D.R. (B) < S.D.R. (A) and so, town B is healthier than town A.
Question 38.
Compute Marshall-Edgeworth’s and Dorbish-Bowley’s price index numbers from the following data:

Answer:



Question 39.
Population figures for a-city are given below:

Fit a curve of the type Y = abx and estimate the population for the year 2014.
Answer:
The exponential curve is : Y = abx
The normal equations are : n loga + logb. Σx = Σloga (1)
Σ x + logb Σx2 = logy …… (2)
Let x and y be the years and the population.

Since Σ x = 0;
From (1)

∴ a = A.L (loga) = A.L (2.1960) = 157.036
From (2)

∴ b = A.L (logb) = A.L (0.0399) = 1,0962
The fitted exponential trend equation is:
y = abx
ŷ = 157.036(1.0962)x
Estimation of the population for the year 2014; x = 4;
ŷ(2014) = 157.036 (1.962)4 = 226.7905 (000’s)
Question 40.
Five unbiased coins are tossed 128 times and the frequencies of number heads are noted below. Fit a Binomial distribution. Test at 5% L. O. S. that it is a good fit.

Answer:
Let x be the number of heads obtained is a Binomnal variate with the parameters n = 5, and P = \(\frac { 1 }{ 2 }\) = 0.5. Sinpe the coin is unbiased ∴ q = 1 – P = 1 – 0.5 = 0.5 N = 120 (Given as 128 is a misprint). Then the P.m.f. is :
P(x) = nCxPxqn-x, x = 0, 1, 2 …n
= 5Cx(0.5)x(0.5)5-x, n = 0, 1,2 …n
Theoretical / Expected frequence: Tx = P(x) M.
So, T0/E0 = P(x = 0) × 100
= 5Co(0.5)° (0.5)5-0 × 100 = 3.125
Using recurrence relation:

T1 = \(\frac{5+1-1}{1}\left(\frac{0.5}{0.5}\right)\) T1-1 = 5 × 3.125 = 15.625
T0 = \(\frac{5+1-2}{2}\) × 1 × 15.625=31.25
T3 = \(\frac{5+1-3}{3}\) × l × 31.25 = 31.25
T4 = \(\frac{5+1-4}{4}\) × 1 × 31.25 = 15.625 4
T5 = \(\frac{5+1-5}{5}\) × 1 × 15.625 = 3.125
The fitted observed and theoretical frequency distribution is

Chi-Square test:
H0: B.D is a good fit (ie.,Oi = Ei)
H1: B.D is not a good fit (i.e., Oi ≠ Ei) {Upper tail test K2}
Under H0, the χ2– test statistic is :
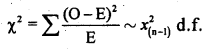
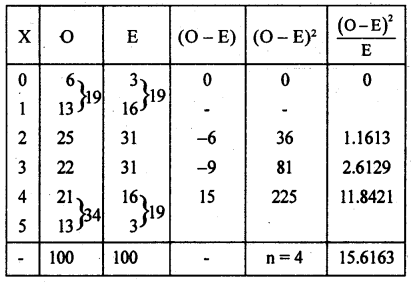
χ2cal = 15.6163
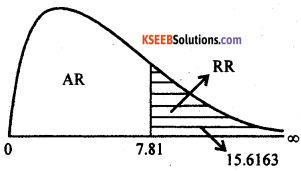
At α = 5% L.O.S for (n – 1) = 4 – 1 = 3 d.f the upper tail critical value K2 = 7.81
Here χ2cal lies in RR
∴ H0 is rejected and H1 is accepted.
Conclusion: B.D. is not a good fit.
![]()
Section – E
V. Answer any TWO of the following questions: (2 x 5 = 10)
Question 41.
The weights of 1000 students are normally distributed with mean 55 kgs and S.D. 3 kgs. Find the number of students with weight between 57 kgs and 60 kgs.
Answer:
Let x be the weights is a normal variate with mean: μ = 55 kgs and S.D: σ = 3kgs. N = 1000
Then S.N.V
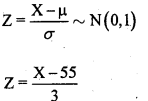
No of students with weight between 57kg and 60kg
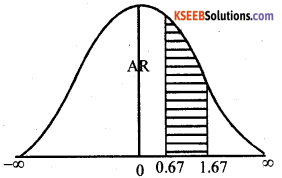
= p(57 < ×< 60)
\(=\mathrm{P}\left(\frac{27-55}{3}<\mathrm{Z}<\frac{60-55}{3}\right)\)
= P(0.67 < Z < 1.67)
= Area from 0.67 to 1.67
= Area from 0.67 to ∞ – Area from 1.67
= 0.2514 – 0.0475
= 0.2039 × 1000
= 203.9 ≅ 204
Question 42.
A random sample of 100 people from a city in the year 2011 revealed that 65 were cricket match viewers. Another random sample of 100 people from same city in the year 2013 revealed that 75 were cricket match viewers. Examine whether there is a significant increase in proportion of cricket match viewership at 1% level of significance.
Answer:
n1 = 100; x1, = 65; n2 100; x2 = 75
H0: Proportion of cricket viewers in two years are same (i.e., P01 = P02)
H1: Proportion of cricket viewers has increased in two years (i.e.,P01 < P02) {Lower tail test}
Under H0, the test statistic is:
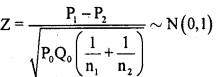
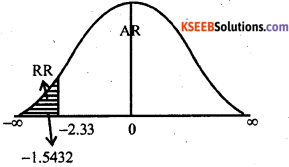

At 1% the lower tail critical value -K = -2.33
Here Zcal lies in A.R. ∴ H0 is Accepted.
Conclusion: P01 = P02
Question 43.
From the following data, test whether ‘education’ and ‘employment’ are independent at 5% level of significance.
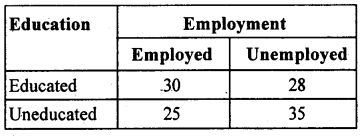
Answer:
H0: Education and employment are independent
H1: Education and employment are dependent.
The given data can be written in a 2 × 2 contingency table as below.
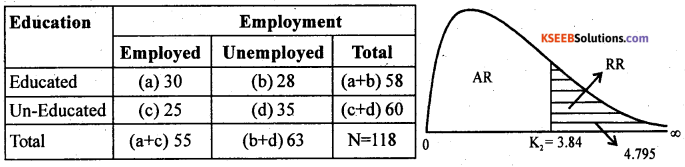
Under H0 the χ2 -test statistics is
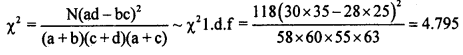
At α = 5% for l.df the upper tail critical value K2 = 3.84. Here χ2 -cal lies in R.R.
∴ H0 is rejected and H1 is Accepted
Conclusion: Education and employment are dependent
![]()
Question 44.
Obtain the value of the game and mention the best strategies of the players.

Answer:
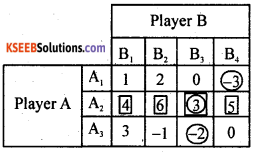
Using maximum-minimax principle –
- Minimum Payoff in each row is/are circled.
- Pay off in each column are/is boxed.
- From the above process the Payoff 3 at (2, 3) is circled as well as boxed, is the saddle point
- The suggested optimal strategies for the players are A2, B3
- The value of the game V = 3