Students can Download Maths Chapter 9 Differential Equations Ex 9.2 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 9 Differential Equations Ex 9.2
2nd PUC Maths Differential Equations NCERT Text Book Questions and Answers Ex 9.2
In each of the Exercises 1 to 10 verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:
Question 1.
y = ex + 1 : y’’- y’ = 0
Answer:
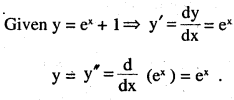
Given, y’’- y’= ex – ex =0
∴ Hence given function is solution of
corresponding differential equation.
Question 2.
y5= x2 + 2x + C : y’ – 2x – 2 = 0
Answer:
Given y = x2 + 2x + C
⇒ \(y^{\prime}=\frac{d}{d x}\) to + 2x + C) = 2x + 2
Given, y’ = 2x -2 = 2x + 2 – 2x – 2 = 0
LHS = RHS
Hence y = x2 + 2x + C, is solution of given differential equation.
![]()
Question 3.
y = cos x + C : y’+ sin x = 0
Answer:
Given y = cos x + C
⇒ \(y^{\prime}=\frac{d}{d x}\) (cos x + C) = – sin x
Given, y’ + sinx = 0sinx + sinx = 0
LHS = RHS
Hence y = cos x + C, is solution of given differential equation.
Question 4.
\(y=\sqrt{1+x^{2}} \quad: y^{\prime}=\frac{x y}{1+x^{2}}\)
Answer:

(1) and (2), Hence \(y=\sqrt{\left(1+x^{2}\right)}\)is solution of given differential equation.
Question 5.
y = Ax : xy’ = y (x ≠ 0)
Answer:
Given, y = Ax ⇒ y’=A
Given, x y’ = y ⇒ x x A = Ax => Ax = Ax
Hence y = Ax, is solution of given differential equation.
Question 6.
\({ y }={ x }\sin { x } \quad :{ x }{ y }^{ \prime }={ y }+{ x }\sqrt { { x }^{ 2 }-{ y }^{ 2 } } \\ (x\neq 0{ \quad and }\quad x\quad >\quad y{ \quad or }\quad x<-y)\)
Answer:
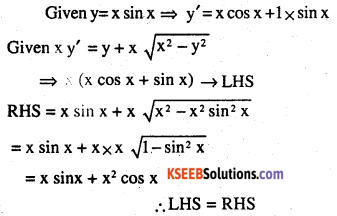
![]()
Question 7.
\(x y=\log y+C \quad: y^{\prime}=\frac{y^{2}}{1-x y}(x y \neq 1)\)
Answer:
Given xy = log y + C
Differentiating w.r.t x, we get
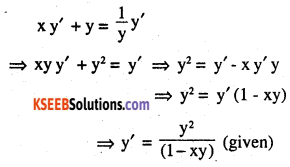
Hence xy = log y + C, is a solution of given differential equation.
Question 8.
y – cos y = x : (y sin y + cos y + x) y’ = y
Answer:
Given y-cos y = x ⇒ x + cos y = y …(1)
Differentiating w.r.t x, we get
⇒ y’+sin yy’= 1 ⇒ y'(1+sin y)= 1 ….(2)
LHS = (y sin y + cos y + x) y’ ………… (3)
putting (1) in (3) = (y sin y + y) y’
= {y (siny +1)} y’
= { y'(1+ siny)} y putting (2) in (3)
= 1 x y = y = RHS
LHS = RHS
Hence y – cos y = x, is solution of given differential equation.
Question 9.
x + y = tan1 y : y2 y’ + y2 + 1 = 0
Answer:
x + y = tan-1 y (given) .
differentiating w.r.t x
\(1+\mathrm{y}^{\prime}=\frac{1}{\left(1+\mathrm{y}^{2}\right)}\left(\mathrm{y}^{\prime}\right) \Rightarrow\left(1+\mathrm{y}^{\prime}\right)\left(1+\mathrm{y}^{2}\right)=\mathrm{y}^{\prime}\)
⇒ 1+ y’ + y2 + y2 y’ = y’
⇒ 1 + y2 + y2 y’ = 0
⇒ y2 y’ + y2 + 1 = 0 (given)
Hence x + y = tan’1 y, is solution of given differential equation.
![]()
Question 10.
\(\begin{aligned}y=& \sqrt{a^{2}-x^{2}} & x \in(-a, a): x+y \frac{d y}{d x}=0(y \neq 0)\end{aligned}\)
Answer:

Hence \(y=\sqrt{a^{2}-x^{2}}\), is solution of given differential equation.
Question 11.
The number of arbitrary constants in the general solution of a differential equation of fourth order are:
(A) 0
(B) 2
(C) 3
(D) 4
Answer:
The number of arbitrary constants in general solution of a differential equation of nth order is n. Hence answer is (D) 4.
![]()
Question 12.
The number of arbitrary constants in the particular solution of a differential equation of third order are:
(A) 3
(B)2
(C)1
(D) 0
Answer:
In particular solution of differential equation, there is no arbitrary constant. Hence answer is (D) 0.