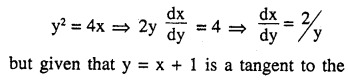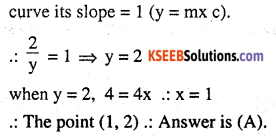Students can Download Maths Chapter 6 Application of Derivatives Ex 6.3 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 6 Application of Derivatives Ex 6.3
2nd PUC Maths Application of Derivatives NCERT Text Book Questions and Answers Ex 6.3
Question 1.
Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
Answer:
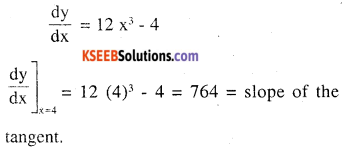
Question 2.
Find the slope of the tangent to the curve
\(y=\frac{x-1}{x-2}, x \neq 2 \text { at } x=10 \)
Answer:
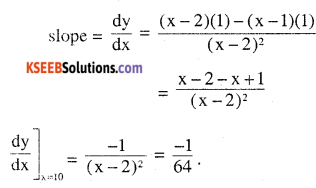
Question 3.
Find the slope of the tangent to curve y = x3 – x + 1 at the point whose x- coordinate is 2.
Answer:
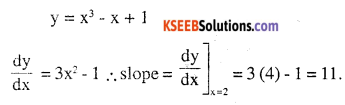
Question 4.
Find the slope of the tangent to the curve y = x3 – 3x + 2 at the point whose x-coordinate is 3.
Answer:
\(\frac{d y}{d x}\) = 3x2 – 3 dx
slope at x = 3 is 3 (9) – 3 = 24.
![]()
Question 5.
Find the slope of the normal to the curve
\(x=a \cos ^{3} \theta, y=a \sin ^{3} \theta \text { at } \theta=\frac{\pi}{4}\)
Answer:
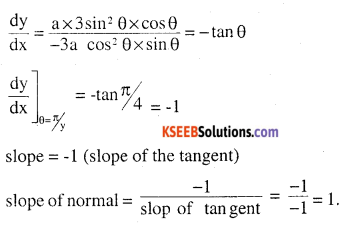
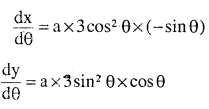
Question 6.
Find the slope of the normal to the curve
\(x=1-a \sin \theta, y=b \cos ^{2} \theta \text { at } \theta=\frac{\pi}{2}\)
Answer:
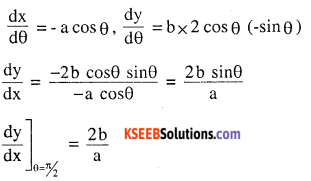
Question 7.
Find points at which the tangent to the curve y = x3 – 3x2 – 9x + 7 is parallel to
the x-axis.
Answer:
\(\frac{d y}{d x}\) = 3x2 – 6x – 9, slope of the tangent
since the tangent is parallel to x-axis \(\frac{d y}{d x}\) = 0
3x2 – 6x – 9 = 0
3 (x + 1) (x – 3) = 0, x = 3, x = -1
when x = 3, y = 27 – 27 – 27 4- 7 = -20
when x = -1, y = -1 -3 + 9 + 7 = 12
The points at which the tangent parallel to x – axis are (3, -20) and (-1, 12).
Question 8.
Find a point on the curve y = (x – 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Answer:
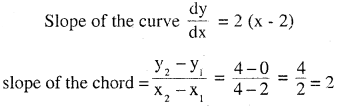

Question 9.
Find the point on the curve y = x3 – 11x + 5 at which the tangent is y = x – 11.
Answer:
Slope of the line y = x – 11 is 1
slope of the curve \(\frac{d y}{d x}\) = 3x2 – 11
∴ 3x2 – 11 = 1 ‘
3x2 = 12 ⇒ x2 = 4, x = +2
when x = 2, y = (2)3 – 11 (2) + 5 = -9
when x = -2, y = -8 + 22 + 5 = 19
points are (2, -9) and (-2, 19)
equation of tangent at (2, -9) and slope is 1
y + 9 = 1 (x – 2)
y = x- 11 equation of tangent at (-2, 19)
y – 19 = 1 (x + 2) ⇒ y = x + 211
∴ (2, -9) is the only point at which the tangent is y = x – 11.10.
![]()
Question 10.
Find the equation of all lines having slope – 1 that are tangents to the curve
\(y=\frac{1}{x-1}, x \neq 3\)
Answer:
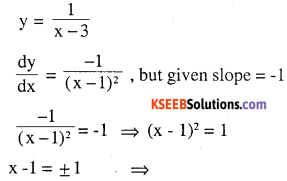
x = 2, x = 0
when x = 2, y = 1
when x = 0, y = -1
The points are (2, 1) and (0,-1)
equation of line though (2,1) having slope = -1
is y – 1 = -1 x (x – 2) ⇒ y + x = 3
or x + y – 3 = 0 and equation of line through (0,- 1)y + 1 = -1 (x – 0)
∴ y + x + 1 = 0.
Question 11.
Find the equation of all lines having slope 2 which are tangents to the curve
\(y=\frac{1}{x-3}, x \neq 3\)
Answer:
slope of the line = 2
slope of the curve = \(\frac{-1}{(x-3)^{2}}\)
\(\frac{-1}{(x-3)^{2}}\) =2
⇒ 2 (x -3)2 = -1
⇒ 2 (x2 – 6x + 9) = -1
⇒ 2x2 – 12x + 19 = 0
which has no real roots b2 – 4ac < 0
hence there is no point on the curve.
Question 12.
Find the equations of all lines having slope 0 which are tangent to the curve
\(y=\frac{1}{x^{2}-2 x+3}\)
Answer:
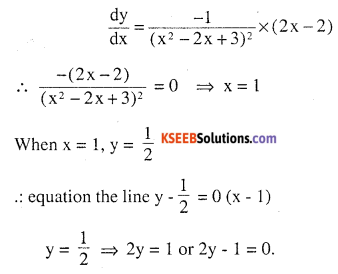
Question 13.
Find the points of curve \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\) which the tangents are
(i) parallel to x-axis
(ii) parallel to y-axis.
Answer:
16x2 + 9y2 = 144
16 x 2 x + 9 x 2y x \(\frac{d y}{d x}\) = 0
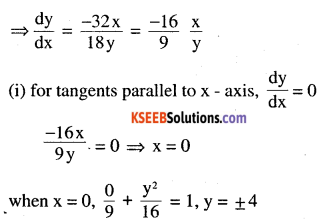
(0,4) and (0, -4) are the points on the curve at which tangent is parallel to x – axis.
![]()
(ii) For tangents parallel to y – axis \(\frac{d y}{d x}\) = \(\frac{1}{0}\)
\(\frac{-16 x}{9 y}=\frac{1}{0} \Rightarrow y=0\)
when y = 0, x2 = 9x = ± 3 point is (3,0) and (-3,0)
(3, 0) and (-3, 0) are the points at which the curve is parallel to y – axis.
Question 14.
Find the equations of the tangent and normal to the given curves at the indicated points:
(i) y = x4 – 6x3 + 13x2 – 10x + 5 at (0, 5)
Answer:
y = x4 – 6x3 + 13x2 – 10x + 5 at (0, 5) dy
\(\frac{d y}{d x}\) = 4x3 – 18x2 + 26x – 10 dx
slope at (0,5) = -10
∴ Equation of tangent at (0, 5) is
y – 5 = -10 (x – 0)
y – 5 = -10 x 10 x + y – 5 = 0
slope of the normal at (0,5)
\((0,5)=\frac{-1}{-10}=\frac{1}{10}\)
∴ equation of normal is
y – 5 =\(\frac{1}{10}\) (x – 0) = 10y – 50 = x
x – 10y + 50 = 0
(ii) y = x4 – 6x3 + 13x2 – 10x + 5 at (1, 3)
Answer:
\(\frac{d y}{d x}\) = 4x3 – 18x2 + 26x – 10 dx
slope of the tangent at x = 1
(iii) y = x3 at (1,1)
Answer:
\(\frac{d y}{d x}=3 x^{2}\)
∴ slope of the tangent at x = 1 = 3
∴ Equation of tangent is y – 1 = 3(x – 1)
3x – y – 2 = 0
∴ slope of normal = \(\frac{-1}{3} \)
∴ equation of normal is y – 1 = \(\frac{-1}{3} \)(x – 1)
3y – 3 = – (x – 1)
x + 3y – 4 = 0.
![]()
(iv) y = x2 at (0, 0)
Answer:
\(\frac{d y}{d x}=2 x\)
∴ slope at x = 0 =0
∴ Equation of tangent is y – 0 = 0 (x – 0) ⇒ y = 0
slope of the normal = -1/(0)
∴ equation of normal \(y – 0=\frac{-1}{0}(x-0) \Rightarrow x=0\)
(v) x = cos t, y = sin t at \(\frac{\pi}{4}\)
Answer:


Question 15.
Find the equation of the tangent line to the curve y = x2 – 2x +7 which is
(a) parallel to the line 2x – y + 9 = 0
Answer:
\(\frac{d y}{d x}\) = 2x – 2 also slope = 2
2 x – 2 = 2 ⇒2x = 4 ⇒ x = 2
when x = 2, y = (2)2 – 2 (2) + 7 = 7
∴ equation of tangent is y – 7 = 2 (x – 2)
2x – y + 3 = 0 ⇒ 2x – y + 3 = 0.
(b) perpendicular to the line 5y – 15x = 13.
Answer:
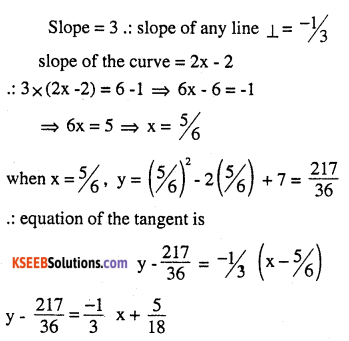
12x + 36y – 227 = 0
Question 16.
Show that the tangents to the curve y = 7x3 + 11 at the points where x = 2 and x = – 2 are parallel.
Answer:
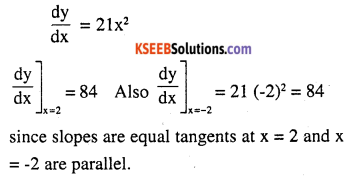
![]()
Question 17.
Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
Answer:
y = x3
\(\frac{d y}{d x}\) = 3x2,
Given that \(\frac{d y}{d x}\) = y = x3
∴ 3x2 = x3 ⇒ x2 (3 – x) = 0 ⇒ x = 0 or x = 3
when x = 3, y = 33 = 27, when x = 0, y = 0
∴ The required points are (0, 0), (3, 27).
Question 18.
For the curve y = 4x3 – 2x5, find all the points at which the tangent passes through the origin.
Answer:
y = 4x3 – 2x5 dy
\(\frac{d y}{d x}\) = 12x2 – 10x4 dx
Let (a, b) be the point on the curve at which the tangent passes through the origin.
∴ Equation of tangent is
y – b = (12a2 – 10a2) (x – a)
but this passes through the origin
∴ 0 – b = (12a2 – 10a4) (-a) b = 12a3 – 10a5 ….(1)
Also from the equation b = 4a3 – 2a5 …. (2)
from (1) and (2) 12a3 – 10a5 = 4a3 – 2a5
8a3 = 8a5
a3 (1 – a2) = 0 ⇒ a = 0, a = + 1
when a = 0, b = 0, (0, 0)
a = 1,b= 12(1)- 10(1) = 2, (1,2)
a = -1, b = 12 (-1) -10 (-1) = -2, (-1, -2)
Hence the required points are (0,0), (1,2), (-1,-2).
Question 19.
Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to the x-axis.
Answer:

![]()
Question 20.
Find the equation of the normal at the point (am2,am3) for the curve ay2 = x3.
Answer:

Question 21.
Find the equation of the normal to the curve y = x3 + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
Answer:
y = x3 + 2x + 6
\(\frac{d y}{d x}\) = 3x2+ 2
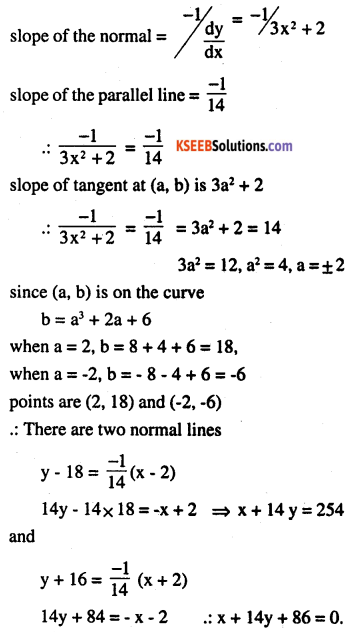
Question 22.
Find the equations of the tangent and normal to the parabola y2 = 4ax at the
point (at2, 2at).
Answer:

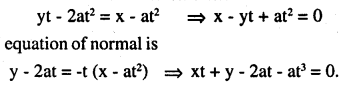
Question 23.
Prove that the curves x = y2 and xy = k cut at right angles* if 8k2 = 1.
Answer:

Question 24.
Find the equations of the tangent and normal to the hyperbola
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) at the point (x0, y0)
Answer:
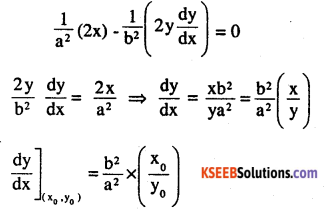

Question 25.
Find the equation of the tangent to the curve
\(y=\sqrt{3 x-2}\) which is parallel to the line 4x – 2y +5 = 0
Answer:

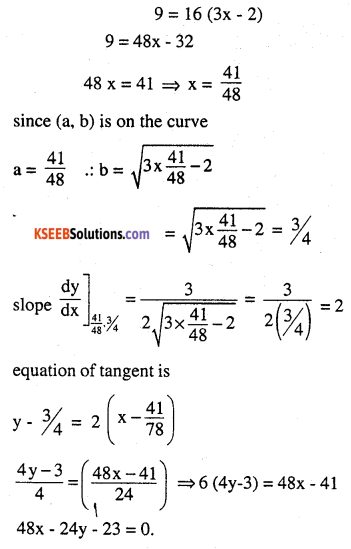
![]()
Choose the correct answer in Exercises 26 and 27.
Question 26.
The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is
(A) 3
(B) 1/3
(C) -3
(D) -1/3
Answer:

Question 27.
The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(A) (1, 2)
(B) (2,1)
(C) (1, – 2)
(D) (- 1, 2)
Answer: