Students can Download Maths Chapter 4 Determinants Ex 4.2 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 4 Determinants Ex 4.2
2nd PUC Maths Determinants NCERT Text Book Questions and Answers Ex 4.2
Using die property of determinants and without prove the following Q. 1-5
Question 1.
\(\left|\begin{array}{lll}{\mathbf{x}} & {\mathbf{a}} & {\mathbf{x}+\mathbf{a}} \\{\mathbf{y}} & {\mathbf{b}} & {\mathbf{y}+\mathbf{b}} \\{\mathbf{x}} & {\mathbf{c}} & {\mathbf{x}+\mathbf{c}}\end{array}\right|=\mathbf{0}\)
Answer:

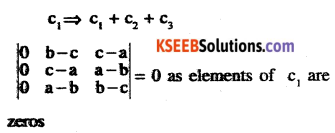
Question 2.
\(\left|\begin{array}{ccc}{\mathbf{a}-\mathbf{b}} & {\mathbf{b}-\mathbf{c}} & {\mathbf{c}-\mathbf{a}} \\{\mathbf{b}-\mathbf{c}} & {\mathbf{c}-\mathbf{a}} & {\mathbf{a}-\mathbf{b}} \\{\mathbf{c}-\mathbf{a}} & {\mathbf{a}-\mathbf{b}} & {\mathbf{b}-\mathbf{c}}\end{array}\right|=\mathbf{0}\)
Answer:
Question 3.
\(\left|\begin{array}{lll}{2} & {7} & {65} \\{3} & {8} & {75} \\{5} & {9} &{86}\end{array}\right|=0\)
Answer:
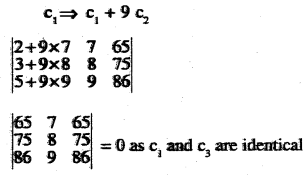
![]()
Question 4.
\(\left|\begin{array}{lll}{\mathbf{1}} & {\mathbf{b} \mathbf{c}} & {\mathbf{a}(\mathbf{b}+\mathbf{c})} \\{\mathbf{1}} & {\mathbf{c} \mathbf{a}} & {\mathbf{b}(\mathbf{c}+\mathbf{a})} \\{\mathbf{1}} & {\mathbf{a} \mathbf{b}} & {\mathbf{c}(\mathbf{a}+\mathbf{b})}\end{array}\right|=\mathbf{0}\)
Answer:
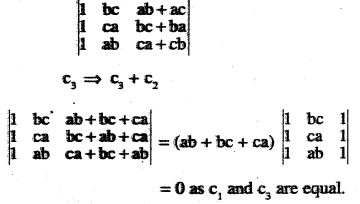
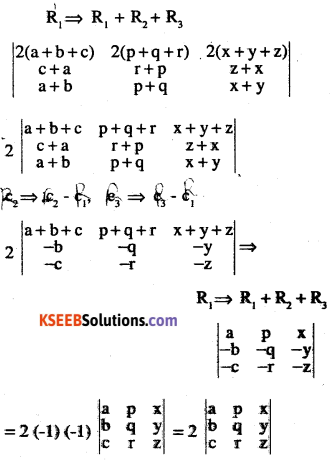
Question 5.
\(\left|\begin{array}{ccc}{\mathbf{b}+\mathbf{c}} & {\mathbf{q}+\mathbf{r}} & {\mathbf{y}+\mathbf{z}} \\{\mathbf{c}+\mathbf{a}} & {\mathbf{r}+\mathbf{p}} & {\mathbf{z}+\mathbf{x}} \\{\mathbf{a}+\mathbf{b}} & {\mathbf{p}+\mathbf{q}} & {\mathbf{x}+\mathbf{y}}\end{array}\right|=\mathbf{2}\left|\begin{array}{ccc}{\mathbf{a}} & {\mathbf{p}} & {\mathbf{x}} \\{\mathbf{b}} & {\mathbf{q}} & {\mathbf{y}} \\{\mathbf{c}} & {\mathbf{r}} & {\mathbf{z}}\end{array}\right|\)
Answer:
By using properties of determination .show that
![]()
Question 6.
\(\left|\begin{array}{ccc}{\mathbf{0}} & {\mathbf{a}} & {\mathbf{-} \mathbf{b}} \\{-\mathbf{a}} & {\mathbf{o}} & {\mathbf{-c}} \\{\mathbf{b}} & {\mathbf{c}} & {\mathbf{0}}\end{array}\right|=\mathbf{0}\)
Answer:

Question 7.
\(\left|\begin{array}{ccc}{-a^{2}} & {a b} & {a c} \\{b a} & {-b^{2}} & {b c} \\{c a} & {c b} & {-c^{2}}\end{array}\right|=4 a^{2} b^{2} c^{2}\)
Answer:

Question 8.
(i)
\(\left| \begin{array}{ccc} { 1 } & { a } & { a^{ 2 } } \\ 1 & b & { b }^{ 2 } \\ { 1 } & { c } & { c^{ 2 } } \end{array} \right| =(a-b)(b-c)(c-a)\)
Answer:
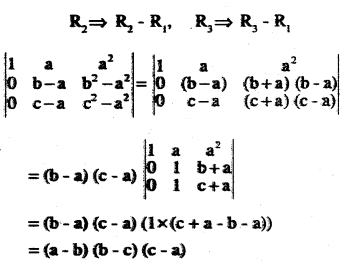
![]()
(ii)
\(\left| \begin{array}{lll} { { l } } & { { 1 } } & { { 1 } } \\ { { a } } & { { b } } & { { c } } \\ { { a }^{ { 3 } } } & { { b }^{ { 3 } } } & { c }^{ { 3 } } \end{array} \right| \)
Answer:
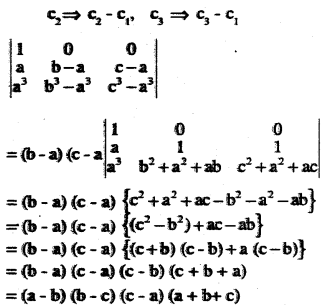
Question 9.
\(\left|\begin{array}{lll}{\mathbf{x}} & {\mathbf{x}^{2}} & {\mathbf{y} \mathbf{z}} \\{\mathbf{y}} & {\mathbf{y}^{2}} & {\mathbf{z} \mathbf{x}} \\{\mathbf{z}} & {\mathbf{z}^{2}} & {\mathbf{x} \mathbf{y}}\end{array}\right|\)
Answer:

Question 10.
(i)
\(\left|\begin{array}{ccc}{x+4} & {2 x} & {2 x} \\{2 x} & {x+4} & {2 x} \\{2 x} & {2 x} & {x+4}\end{array}\right|=(5 x+4)(4-x)^{2}\)
Answer:

![]()
(ii)
\(\left|\begin{array}{ccc}{\mathbf{y}+\mathbf{K}} & {\mathbf{y}} & {\mathbf{y}} \\{\mathbf{y}} & {\mathbf{y}+\mathbf{k}} & {\mathbf{y}} \\{\mathbf{y}} & {\mathbf{y}} & {\mathbf{y}+\mathbf{k}}\end{array}\right|=\mathbf{k}^{2}(5 \mathbf{y}+\mathbf{k})\)
Answer:
R1⇒ R1 + R2 + R3

Question 11.
(i)
\(\left|\begin{array}{ccc}{\mathbf{a}-\mathbf{b}-\mathbf{c}} & {\mathbf{2 a}} & {\mathbf{2} \mathbf{a}} \\{\mathbf{2} \mathbf{b}} & {\mathbf{b}-\mathbf{c}-\mathbf{a}} & {\mathbf{2} \mathbf{b}} \\{\mathbf{2 c}} & {\mathbf{2 c}} & {\mathbf{c}-\mathbf{a}-\mathbf{b}}\end{array}\right|=(\mathbf{a}+\mathbf{b}+\mathbf{c})^{3}\)
Answer:

![]()
(ii)
\(\left|\begin{array}{ccc}{\mathbf{x}+\mathbf{y}+2 \mathbf{z}} & {\mathbf{x}} & {\mathbf{y}} \\{\mathbf{z}} & {\mathbf{y}+\mathbf{z}+2 \mathbf{x}} & {\mathbf{y}} \\{\mathbf{z}} & {\mathbf{x}} & {\mathbf{z}+\mathbf{x}+2 \mathbf{y}}\end{array}\right|=2(\mathbf{x}+\mathbf{y}+\mathbf{z})^{3}\)
Answer:
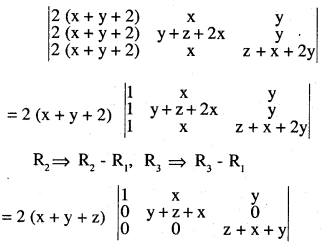
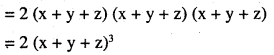
Question 12.
\(\left|\begin{array}{ccc}{\mathbf{1}} & {\mathbf{x}} & {\mathbf{x}^{2}} \\{\mathbf{x}^{2}} & {\mathbf{1}} & {\mathbf{x}} \\{\mathbf{x}} & {\mathbf{x}^{2}} & {\mathbf{1}}\end{array}\right|=\left(1-\mathbf{x}^{3}\right)^{2}\)
Answer:

![]()
Question 13.
\(\left|\begin{array}{ccc}{1+a^{2}-b^{2}} & {2 a b} & {-2 b} \\{2 a b} & {1-a^{2}+b^{2}} & {2 a} \\{2 b} & {-2 a} & {1-a^{2}-b^{2}}\end{array}\right|=\left(1+a^{2}+b^{2}\right)^{3}\)
Answer:

Question 14.
\(\left|\begin{array}{ccc}{\mathbf{a}^{2}+\mathbf{1}} & {\mathbf{a} \mathbf{b}} & {\mathbf{a c}} \\{\mathbf{a b}} & {\mathbf{b}^{2}+\mathbf{1}} & {\mathbf{b c}} \\{\mathbf{c a}} & {\mathbf{c b}} &{\mathbf{c}^{2}+\mathbf{1}}\end{array}\right|=\mathbf{1}+\mathbf{a}^{2}+\mathbf{b}^{2}+\mathbf{c}^{2}\)
Answer:

Question 15.
Let A be a square matrix of order 3 x 3 then |KA| is equal to
(A) K |A|
(B) K2 |A|
(C) K3 |A|
(D) 3K |A|
Answer:
|KA| = K3 |A|
hence (C) is the correct answer.
![]()
Question 16.
Which of the following is true
(A) Determinant is a square matrix
(B) Determinant is a member associated to a matrix
(C) Determinant is a number associated with a square matrix.
(D) None of these
Answer:
Determinant is a number associated with . a square matrix hence the answer is (C).