Students can Download 2nd PUC Maths Previous Year Question Paper June 2017, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Previous Year Question Paper June 2017
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions
- The question paper has five parts namely A, B, C, D, and E. Answer all the parts.
- Use the graph sheet for the question on Linear programming in Part – E
Part – A
Answer ALL the following questions: (10 × 1 = 10)
Question 1.
Find the identity element for the binary operation *, defined on the set Q of rational numbers by a * b = \(\frac{a b}{4}\)
Solution:
Let e be the identity element.
a * e = a
⇒ \(\frac{a e}{4}\) = a
⇒ e = 4
Question 2.
Write the values of x for which \(\tan ^{-1} \frac{1}{x}=\cot ^{-1} x\), holds.
Solution:
x > 0
![]()
Question 3.
Construct a 2 × 2 matrix, A = [aij], whose elements are given by, aij = \(\frac{i}{j}\)
Solution:

Question 4.
Find the values of x for which \(\left|\begin{array}{ll}3 & x \\x & 1\end{array}\right|=\left|\begin{array}{ll}3 & 2 \\4 & 1\end{array}\right|\)
Solution:
3 – x2 = 3 – 8
⇒ x2 = 8
⇒ x = ±√8 = ±2√2
Question 5.
Find \(\frac{d y}{d x}\), if y = sin (x2)
Solution:
\(\frac{d y}{d x}\) = cos(x2) . 2x
![]()
Question 6.
Find ∫cos 3x dx
Solution:
\(\frac{\sin 3 x}{3}+c\)
Question 7.
Find unit vector in the direction of vector \(\hat{i}+\hat{j}+2 \hat{k}\)
Solution:
\(\hat{a}=\frac{\vec{a}}{|\vec{a}|}=\frac{\hat{i}+\hat{j}+2 \hat{k}}{\sqrt{6}}\)
Question 8.
Write the direction cosines of the y-axis.
Solution:
0, 1, 0
Question 9.
Define the optimal solution in a linear programming problem.
Solution:
Any feasible solution of LPP which maximizes or minimizes the objective function is called an optimal solution.
![]()
Question 10.
If P(A) = 0.8 and P(B|A) = 0.4 then find P(A∩B).
Solution:
P(A∩B) = P(A) × P(B/A)= 0.8 × 0.4 = 0.32
Part – B
Answer any TEN questions: (10 × 2 = 20)
Question 11.
Show that if f : A → B and g : B → C are onto, then gof : A → C is also onto.
Solution:
Given an arbitrary element z – C, there exists a pre-image y of z under g such that g(y) = z i.e., g is onto. Further, for y ∈ B, there exists an element x in A with f(x) = y, since f is onto. Therefore, gof(x) = g(fx)) = g(y) = z, showing that gof is onto.
Question 12.
Show that \(2 \tan ^{-1} x=\cos ^{-1} \frac{1-x^{2}}{1+x^{2}}, x \geq 0\)
Solution:

Question 13.
Find the value of \(\sin ^{-1}\left(\sin \frac{3 \pi}{5}\right)\)
Solution:
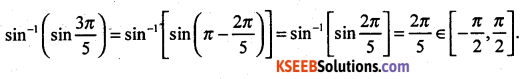
Question 14.
Using the determinant method, find the area of the triangle whose vertices are (1, 0), (6, 0) and (4, 3).
Solution:

Question 15.
Differentiate (sin x)x with respect to x.
Solution:

![]()
Question 16.
Find \(\frac{d y}{d x}\), if 2x + 3y = sin y.
Solution:
Differentiate both sides w.r.t x
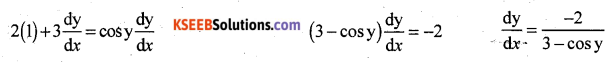
Question 17.
Find the point on the curve \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\) at which the tangents are parallel to x-axis.
Solution:
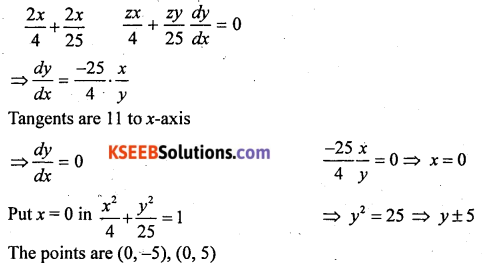
Question 18.
Evaluate: \(\int \frac{\sqrt{\tan x}}{\sin x \cos x} d x\)
Solution:

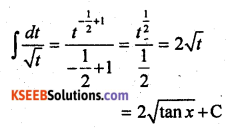
Question 19.
Evaluate: \(\int \frac{x-3}{(x-1)^{3}} e^{x} d x\)
Solution:

Question 20.
Find the order and degree, if defined of the differential equation \(\frac{d^{4} y}{d x^{4}}+\sin \left(\frac{d^{3} y}{d x^{3}}\right)=0\)
Solution:
Order = 4
Degree = not defined.
![]()
Question 21.
If \(\vec{a}\) is a unit vector and \((\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8\), then find \(\vec{x}\)|.
Solution:
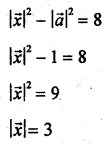
Question 22.
Find the area of the parallelogram whose adjacent sides are given by the vector \(\vec{a}=3 \hat{i}+\hat{j}+4 \hat{k}\) and \(\vec{b}=\hat{i}-\hat{j}+\hat{k}\)
Question 23.
Find the angle between the pair of lines given by \(\vec{r}=2 \hat{i}-5 \hat{j}+\hat{k}+\lambda(3 \hat{i}+2 \hat{j}+6 \hat{k})\) and \(\vec{r}=7 \hat{i}-6 \hat{k}+\mu(\hat{i}+2 \hat{j}+2 \hat{k})\)
![]()
Question 24.
If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) P(B’).
Solution:
P(Atleast one of A or B) = P(A ∪ B) [∵ A and B are independent events]
= P(A) + P(B) – P(A ∩ B)
= P(A) + P(B) – P(A) . P(B)
= P(A) + P(B) – (1 – P(A))
= 1 – P(A’) + P(B) P(A’)
= 1 – [P(A’) + P(B)P(A’)]
= 1 – P(A’) [1 – P(B)]
= 1 – P(A’) P(B’)
= RHS.
Part – C
Answer any TEN questions: (10 × 3 = 30)
Question 25.
Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive or symmetric.
Solution:
R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}
2 ∈ A, But (2, 2) ∉ R
∴ R is not reflexive
(2, 3) ∈ R, But (3, 2) ∉ R
∴ R is not Symmetric
![]()
Question 26.
Solve : tan-1 2x + tan-1 3x = \(\frac{\pi}{4}\). Find the value of ‘x’.
Solution:
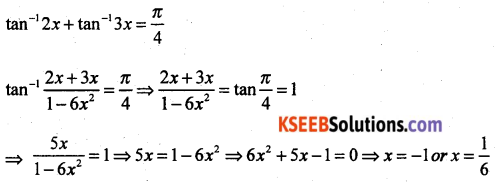
Since x = -1 does not satisfy the equation, x =\(\frac{1}{6}\) is the only solution of the given equation.
Question 27.
By using elementary transformations, find the inverse of A = \(\left[\begin{array}{rr}1 & 2 \\2 & -1\end{array}\right]\)
Solution:
A = I A
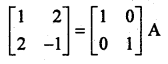

Question 28.
Find \(\frac{d y}{d x}\), if x = a (cos t + log tan\(\frac{t}{2}\)], y = a sin t.
Solution:

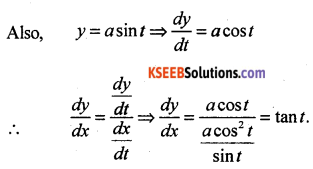
![]()
Question 29.
Verify Mean Value Theorem for the function f(x) = x2 in the interval [2, 4].
Solution:
The function f(x) = x2 is continuous in {2, 4} and differentiable in {2, 4} as its derivative f(x) = 2x is defined in (2, 4).
Now f(2) = 4 and f(4) = 16. Hence
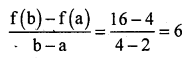
MVT states that there is a point c ∈ (2, 4) such that f'(c) = 6. But f'(x) = 2x which implies c = 3.
Thus at c = 3 ∈ (2, 4), we have f'(c) = 6.
Question 30.
Find two positive numbers whose sum is 15 and the sum of whose squares is minimum.
Question 31.
Evaluate: \(\int \frac{x}{(x+1)(x+2)} d x\)
Solution:

Question 32.
Evaluate: \(\int \frac{x \cos ^{-1} x}{\sqrt{1-x^{2}}} d x\)
Solution:
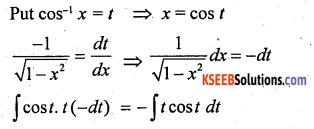
![]()
![]()
Question 33.
Find the area bounded by the curve y = cos x between x = 0 and x = 2π.
Solution:
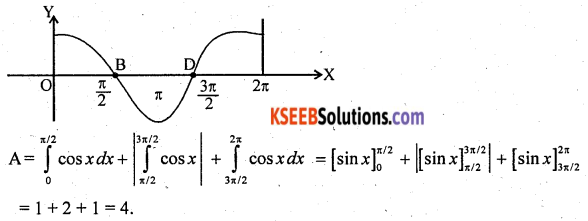
Question 34.
Find the equation of a curve passing through the point (-2, 3), given that the slope of the tangent to the curve at any point (x, y) is \(\frac{2 x}{y^{2}}\)
Solution:

Question 35.
Show that the position vector fo thepoint P, which divides the line joining the points A and B having position vectors \(\vec{a}\) and \(\vec{b}\) internally in the ratio m : n is \(\frac{m \vec{b}+n \vec{a}}{m+n}\).
![]()
Question 36.
Find x such that the four point A(3, 2, 1), B(4, x, 5), C(4, 2, -2) and D(6, 5, -1) are coplanar.
Solution:
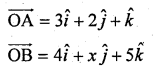

Question 37.
Find the vector and cartesian equations of the plane which passes through the points (5, 2, -4) and perpendicular to the line with direction ratios 2, 3, -1.
Solution:

Question 38.
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
Solution:
P(S1) = Probability that six occurs = \(\frac{1}{6}\)
P(S2) = Probability that six does not occur = \(\frac{5}{6}\)
P(E|S1) = Probability that man reports that six occurs when six has actually on the die = Probability that the truth occurs = \(\frac{3}{4}\)

Part – D
Answer any SIX questions: (6 × 5 = 30)
Question 39.
Prove that the function f : R → R defined by f(x) = 4x + 3 is invertible and find the inverse of f.
![]()
Question 40.
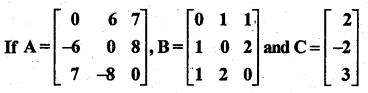
Calculate AC, BC and (A + B)C. Also, verify that (A + B)C = AC + BC.
Solution:
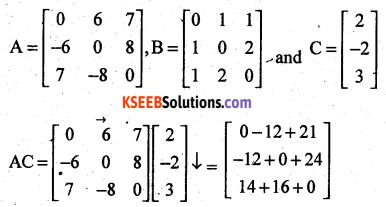
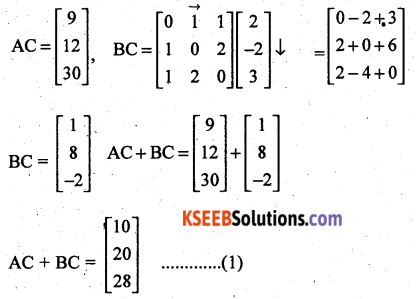

Question 41.
Solve the following system of equations by matrix method.
x – y + z = 6
y + 3z = 11
x – 2y + z = 0
Solution:

Question 42.
If y = 3 cos(log x) + 4 sin(log x), show that x2 y2 + x y1 + y = 0.
Solution:


![]()
Question 43.
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
Solution:
Let r be the radius, h be the height and V be the volume of the sand cone at any time t.

Hence, when the height of the sand cone is 4 cm, its height is increasing at the rate of \(\frac{1}{48 \pi}\) cm/s
Question 44.
Find the integral of \(\sqrt{a^{2}+x^{2}}\) with respect to x and hence evaluate \(\int \sqrt{1+x^{2}} d x\)
Solution:

Question 45.
Find the smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2.
Solution:
The smaller area enclosed by the circle, x2 + y2 = 4 and the line x + y = 2 is represented by the shaded area ACBA.
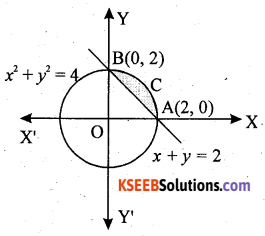
The intersection points of circle and line are A(2, 0) and B(0, 2).
Required area (shown ¡n shaded region)
= Area OACBO – Area (∆OAB)

![]()
Question 46.
Find the general solution of the differential equation y dx – (x + 2y2) dy = 0.
Solution:
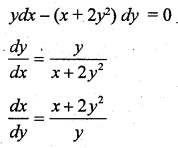

Question 47.
Derive the equation of a line in space passing through two given points both in vector and cartesian form.
Solution:


Question 48.
If a fair coin is tossed 10 times, find the probability of
(i) exactly six heads and
(ii) at least six heads.
Solution:

Part – E
Answer any ONE question: (1 × 10 = 10)
Question 49(a).
Minimize z = -3x + 4y subject to the constraints
x + 2y ≤ 8
3x + 2y ≤ 12
x ≥ 0, y ≥ 0
by graphical method.
Solution:
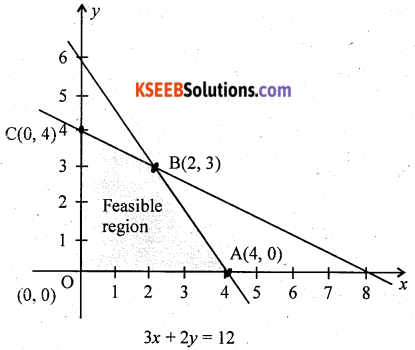
Draw the graph of the line, x + 2y = 8
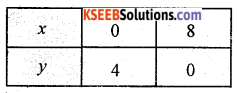
Putting (0, 0) in the inequality x + 2y ≤ 8, we have
0 + 0 ≤ 8
0 ≤ 8 (which is true)
So, the half-plane is towards the origin,
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
Draw the graph of the line, 3x + 2y = 12
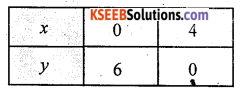
Putting (0, 0) in the inequality 3x + 2y ≤ 12, we have
3 x 0 + 2 x 0 ≤ 12 ⇒ 0 ≤ 12 (which is true)
So, the half-plane is towards the origin,
The feasible region is OABCO.
On solving equations x + 2y = 8 and x = 2 and y = 3
Intersection point B is (2, 3)
The corner points of the feasible region are O(0, 0), A (4, 0) and B(2, 3) and C(0, 4).
The values of Z at these points are as follows:
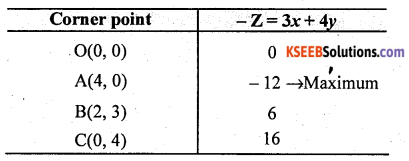
Therefore, the maximum value of Z is -12 at point A(4, 0).
![]()
Question 49(b).
Prove that: \(\left|\begin{array}{ccc}1 & a & a^{2} \\1 & b & b^{2} \\1 & c & c^{2}\end{array}\right|=(a-b)(b-c)(c-a)\)
Solution:


Question 50(a).
Prove that:
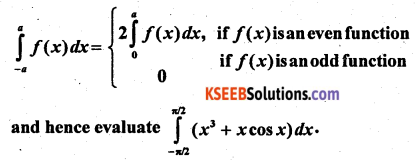
Solution:

f(x) = x3 + x cos x
f(-x) = (-x)3 – x cos (-x) = -x3 – x cos x = -[x3 + x cos x] = -f(x)
∴ f(x) is odd
∴ \(\int_{-\pi / 2}^{\pi / 2}\left(x^{3}+x \cos x\right) d x=0\)
![]()
Question 50(b).
For what value of λ is the function defined by
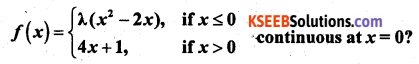
Solution:
When x < 0, f(x) = λ(x2 – 2x) being a polynomial is continous. When x > 0, f(x) = 4x + 1 being a polynomial is continous.
At x = 0
f(0) = λ(02 – 2 × 0) = 0
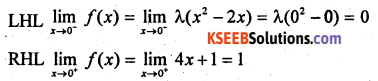
∴ LHL ≠ RHL
∴ lim f(x) does not exists for x = 0
∴ f is discontinous at x = 0 for any value of λ.