Students can Download 2nd PUC Maths Model Question Paper 3 with Answers, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Model Question Paper 3 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 100
Instructions:
- The question paper has five parts namely A, B, C, D and E. Answer all the parts.
- Use the graph sheet for the question on Linear programming in PART E.
Part – A
I. Answer all the questions ( 10 × 1 =10 )
Question 1.
Let * be a binary operation defined on the set of Rational numbers Q defined by a*b = ab + 1 prove that * is a commutative.
Answer:
If * be a commutative binary operation.
a*b = b*a
⇒ a*b = ab + 1 = ba + 1= b*a
∴ * is commutative binary operation on *.
Question 2.
Find the principle value of cos-1(-1/2)
Answer:

Question 3.
Define a diagonal matrix.
Answer:
A square matrix in which except the principle diagonal elements all the elements are zero.
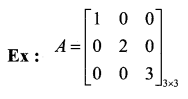
![]()
Question 4.
If A = \(\left[ \begin{matrix} 1 & 2 \\ 4 & 2 \end{matrix} \right]\) then find the value of |2A|.
Answer:
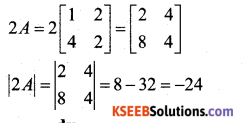
Question 5.
Find \(\frac{\mathrm{d} y}{\mathrm{d} x}\) if y = cos(1 – x).
Answer:
y = cos(1 – x)
Dijf w.rl.x
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) = cox(1 – x)
= -sin(1 – x) x \(\frac{d}{d x}\) (1 – x) dx
= -sin(1 – x)x – 1 = sin(1 – x)
Question 6.
Evaluate ∫(2x – 3 cos x + ex ).dx
=> ∫(2x – 3cosx +ex ).dx
= ∫ 2 x.dx – 3 ∫ cos x.dx + ∫ ex .dx
= 2 x \(\frac{x^{2}}{2}\) – 3 x sinx + e +c
= x2 – 3sin x + ex + c
Question 7.
Define a Unit vector.
Answer:
A vector having Unit magnitude along any vector \(\vec{a}\) is Called a unit vector in the direction of \(\vec{a}\) add is denoted \(\vec{a}|\vec{a}|\) = 1
![]()
Question 8.
If a line makes angle 90°, 60° and 30° with positive direction of x, y and z axis respectively. Find its direction cosines.
Answer:
The Direction cosines are given by.
=(cos90°, cos60°, cos30°).
= (0, 1/2, √3/2 )
Question 9.
In linear programming problems, define linear objectives function.
Answer:
The linear function z = ax + by where a, b are constants which has to be maximised or minimized is called linear objective function.
Question 10.
If P(A) = 0.6 P(B) = 0.3 and P(A ∩B ) = 0.2 find P|A|B).
Answer:
P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{0.2}{0.3}=\frac{2}{3}\)
Part – B
II. Answer any Ten questions :
Question 11.
S.T. function f : N → N by f (1) = f(2) = 1 and f(x) = x -1 for every x > 2, is on to but not one-one.
Answer:
f : N → N by f(1) = f(2) = 1 and f(x) = x – 1.
f is not one-one because
f (1) = 1 and f(2) = 1
∴ f(1) = f(2)
but
1≠2
∴ f is not one-one
for every y ∈ N then
f(x) = y – x – 1 then y = x – 1
⇒ x ∈ N
∴ y ∈ N ∋ x ∈ N
∴ f is onto.
![]()
Question 12.
P.T. tan -1 – cot -1 x = \(\frac{\pi}{2}\) ∀ x ∈R
Answer:
Let tan -1 x = y
x = tan y = cot ( \(\pi / 2\) – y)
cot -1 x = \(\pi / 2\) – y
cot -1 x + y = \(\pi / 2\)
cot -1 x – tan -1 x = \(\pi / 2\)
Question 13.
Write the simplest form of \(\tan ^{-1}(\sqrt{\frac{1-\cos x}{1+\cos x}})\) 0 < x < π
Answer:

Question 14.
Find the equation of a line passing through (3,1) (9,3) using determinants.
Let P(x,y) be the line passing through (3,1) and (9,3)
∴ Let A(3,1) B (9,3)
∴ If P is a point on the line AB then Area of the Δle is zero

∴x(1 – 3) – y(3 – 9) + 1(9 – 9) = 0
-2x – y (-6) + (0) = 0
-2x + 6y = 0
6y = 2x
x = 3 y
∴ Equation of line is x = 3y
Question 15.
if \(\sqrt{x}+\sqrt{y}=\sqrt{10}\) S.T \frac{d y}{d x}+\sqrt{\frac{y}{x}}=0[/latex]
Answer:

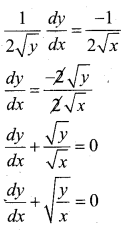
![]()
Question 16.
Find \(\frac{\mathrm{d} \mathbf{y}}{\mathrm{d} \mathbf{x}}\) If y = (log x)cos x
Answer:
y = (log x)cos x
Take log on both side
log y – log(log x)cos x
log y – cos x. log(log x)
Diff w.r.t x, we get
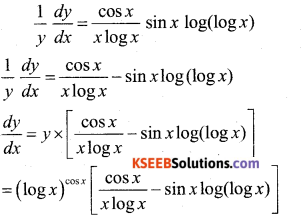
Question 17.
Approximate √36.6 by using differential.
Answer:
y = √x Let x = 36 and Ax = 0.6 then
Δy = \(\sqrt{x+\Delta x}-\sqrt{x}=\sqrt{36.6}-\sqrt{36}=\sqrt{36.6}-6\)
√36.6 = 6 + Δy
Now dy is approximately equal to Ay and is given by.
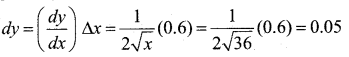
The approximate value of √36.6 is 6+0.05 = 6.05.
Question 18.
Integrate sinx. sin(cosx) w.r.t. x
∫sinx. sin(cosx).dx
Take cos x = t
Diff w.r.t x, we have
-sinx = \(\frac{d t}{d x}\)
-sin x.dx = dt
sin x.dx = -dt
⇒ ∫sin(cosx).sinx.dx
= ∫sin(t)λ – dt = – ∫ sin t.dt
= -x – cos t. + c =cost + c = cos(cosx) + c
![]()
Question 19.
Evaluate \(\int_{0}^{1} \frac{1}{1+x^{2}} \cdot d x\)
Answer:
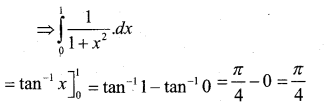
Question 20.
Find the order and degree of differential equation.
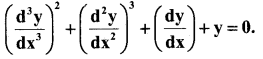
Answer:
order – 3 degree – 2
Question 21.
Find the area of parallelogram whose adjacent sides determine by the vectors.
\(\overrightarrow{\mathrm{a}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{b}}=\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}\)
Answer:
Area of the parallelogram whose adjacent sides are given by.

Question 22.
Obtain the projection of the vector \(\vec{a}=2 \hat{i}+3 \hat{j}+2 \hat{k}\) on the vector \(\overrightarrow{\mathbf{b}}=\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\hat{\mathbf{k}}\)
Answer:

Question 23.
Find the equation of the plane through the inter section of planes 3x – y + 2z – 4 = 0 and x + y – z – 2 = 0 and the point (2,2,1).
Answer:
Equation of any plane through the intersection of the given planes, is of the form.
3x – y + 2z – 4 + λ (x + y – z – 2) = 0
(3 + λ)x + (λ – 1)y + (2 – λ) z – (4 + 2λ) = 0
By Data it is passes through (2,2,1)
⇒ (3 + λ)2 + (λ -1)2 + (2 – λ)1 – (4 + 2λ) = 0
⇒ 6 + 2λ + 2λ – 2 + 2 – λ – 4 – 2λ = 0
⇒ 2 + λ = 0
λ = – 2
Thus the required equation is
(3 – 2)x + (-2 -1 )y + (+2 – 2)1 – (4 + 2(-2) = 0
x – 3y + (0)(1) – (4 – 4) = 0
x – 3y = 0
![]()
Question 24.
A die is thrown. If E is the event the number appearing is a multiple of 3 are F be the event the number appearing is even, then prove that E and F are independent events.
Answer:
A die is thrown the sample space are {1,2,3,4,5,6}
E is the event “the number appearing is a multiple of 3”
E = {3,6} P(E) = \(\frac{n(E)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)
F be the event the number appearing is even
F = {2, 4, 6} P(F) = \(\frac{n(F)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)
⇒ (E∩F) = {6} =P(E∩F) = \(\frac{n(E \cap F)}{n(s)}=\frac{1}{6}\)
∴P(E)
∴ P(E) × P(F) = P(E∩F)
∴ \(\frac{1}{3} \times \frac{1}{2}=\frac{1}{6} \Rightarrow \frac{1}{6}=\frac{1}{6}\)
∴ E and F are independent Events.
Part – C
III. Answer any Ten questions :
Question 25.
Show that the Relation R in the set Z of integers given by R= {(x y) : 2 divides (x-y)} is an Equivalence Relation.
Answer:
→ R – {(xy): 2 divides (x – y) }
→ R is Reflexive as 2 divides (a – a) ∀ a ∈ z.
If (a b) ∈ R then 2 divides a – b.
2 divids b – a Hence (ba)∈R
⇒R is Symmetric.
(ab) ∈ R and (be) ∈ R
⇒ a – b and b-c are divisible by 2
Now a – c = (a – b) + (b – c)
= is even
.’. a – c is divisible by 2.
⇒ R is Transitive
R is Reflexive, Transitive, Symmetric
.’. R is an Equivalence Relation in Z.
![]()
Question 26.
Prove that \(\tan ^{-1} x \tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)\) = \(\tan ^{-1}\left[\frac{3 x-x^{3}}{1-3 x^{2}}\right] \cdot|x|<\frac{1}{\sqrt{3}}\)
Answer:
→ Take tan-1 x = θ ⇒ x = tanθ
![]()

Question 27.
For any square matrix A with Real numbers. Prove that A + A1 is a symmetric and A – A1 is a skew symmetric.
Answer:
Let B = A + A1 then
B1 = (A + A1)1 = A1 + (A1)1
= A1 + A= A + A1 =B
∴ B1 =B ∴B is symmetric matrix
∴ A + A1 is a symmetric matrix.
C = A – A1
C1 = (A – A1 )1 = A1 – (A1)1
= A1 – A = -(A – A1) = -C
C1 = -C is a skew-symmetric matrix.
∴ A – A1 is a skew-symmetric matrix.
Question 28.
If x = a(θ + sinθ) and y = a(1 – cosθ). Prove that \(\frac{d y}{d x}=\tan \frac{\theta}{2}\)
Answer:
⇒ x = a(θ + sinθ)
Diff.w.r.t θ

Question 29.
Verify mean value theorem if f(x) = x2 – 4x – 3 in the interval [ab]
where a = 1 and b = 4.
→ Given f(x) = x2 – 4x – 3
⇒ f1 (x) = 2x – 4 which exists ∀ x in R.
⇒f is derivable for all x in particular it is derivable in
[a b] = [1 4] and hence continuous in[a b]= [ 1 4] Since f is derivable in [1 4 ] ⇒ f is derivable in (1 4).
∴ Both the condition of L.M.V. Theorem as satisfied.
∃ at least one real C in (1 4) ∋
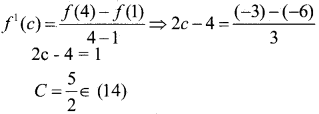
⇒ MVT is verified for f(x) in [14],
Question 30.
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
→ x + y = 60
y = 60 – x
P = xy3
P = x(60 – x)3
P = x(60 – x)3
Diffw.r.t x.
![]()
= x.3(60 – x)2 x (-1) + (60 – x)2.1
= -3x(60 – x)2 + (60 – x)3
= (60 – x)3 – 3x(60 – x)2
=(60 – x)2 [60-x – 3x)
= (60 – x)2 (60 – 4x)
xy3 is to be maximum
\(\frac{d p}{d x}\) = 0
0 = (60-x)2 (60-4x)
60 – 4x = 0
+4x = -60
x = \(\frac{60}{4}\)
x = 15
∴ x = 15 y = 45
x + y = 60
y = 60 – x
= 60 – 15
= 45
![]()
Question 31.
Evaluate ∫sin3x.cos4x.dx.
∫cos4x.sin3x.dx
= ∫ \(\frac{1}{2}\) sin(4x + 3x) – sin(4x -3x)]. dx
= ∫(sin 7x – sin x) dx
= \(\frac{1}{2}\) ∫ sin 7x – ∫\(\frac{1}{2}\) sin x.dx
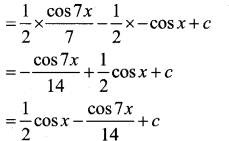
Question 32.
Integrate x2.ex w.r.t x.
answer;

Question 33.
Determine the area of the region bounded by y2 = x and the lines x = 1 and x = 4 and the x-axis in the first quadrant.
Answer:
→ Given that y2 = x
Its a Equation of the Parabola and the Lines x = 1 and x = 4
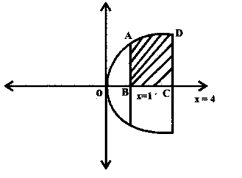
∴ The Required area of the

![]()
Question 34.
Form the differential Equation of the family of circles touching the x-axis at origin.
Answer:
→ Let C denote the family of circles touching x – axis at origin. Let (0,a) be the co-ordinates of the centre of any member of the family.
∴ Equation of family C is. x2 + (y – a)2 = a2
x2 + y2 = 2 ay
Where a is an arbitary constant.
Differentiating both side w.r.t x, we get
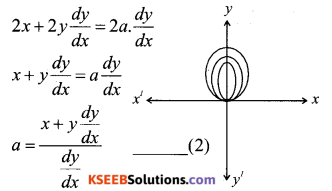
Substitute the value of a from solution. (2) in eqn. (1), we get.
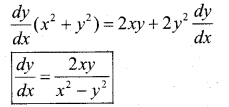
Question 35.
If the two vector \(\overrightarrow{\mathrm{a}}\) and \(\overrightarrow{\mathrm{b}}\) such that \(|\overrightarrow{\mathrm{a}}|\) = 2
\(|\overrightarrow{\mathrm{b}}|\) = 3 and \(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=4\) final \(|\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}|\)
Answer:

Question 36.
Find a Unit Vector perpendicular to each of the vector \((\vec{a}+\vec{b})\) and \((\vec{a}-\vec{b})\).
Where \(\overrightarrow{\mathbf{a}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}\)\(\overrightarrow{\mathbf{b}}=\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}\)
Answer:

Question 37.
Find the shortest distance between the lines l1and l2 whose vector equations are \(\overrightarrow{\mathbf{r}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+\lambda(2 \hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}) and \vec{r}=2 \hat{i}+\hat{j}-\hat{\mathbf{k}}+\mu(3 \hat{\mathbf{i}}-5 \hat{\mathbf{j}}+2 \hat{\mathbf{k}})\)
Answer:

Hence the shortest distance b/w the given lines is given by.
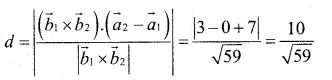
![]()
Question 38.
Bag-I contains 3 red and 4 black balls while another Bag-II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from Bag-II.
Answer:
→ Let E1 be the event of choosing the bag I. E2 be the event of choosing the bag II and A be the event of drawing a red ball.
Then P(E1) = P(E1) = \(\frac{1}{2}\)
P(A / E1) = P (drawing a red ball from Bag I) = \(\frac{3}{7}\)
P(A / E2) = P (drawing a red ball from Bag II) = \(\frac{5}{11}\)
Now, the probability of drawing a ball from Bag – III. being given that it is red, is P(E2/A).
By using Baye’s theorem, we have
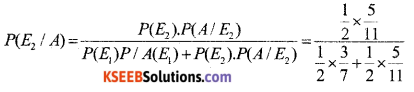
= \(\frac{35}{68}\)
Part – D
IV. Answer the following questions
Question 39.
Prove that the function f:N → N defined by ‘ f(x) = x2 where y = {y:y = x2, x ∈ N} is invertible. Also find the inverse of f.
Answer:
f : N → N defined by f(x) = x2 then ∃ another function g : N →N by g(y) = x.
f(x) = x2
⇒ y = x2
x = √y
∴ g(y) =√y
To show that f is invertible
fog(x) = x
gof(y) = y
fog(x) = f[g(x)]
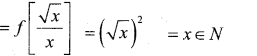
gof(y) = g[f/(y)]
= g[y2] = y ∈N
∴ gof{y) = y ∈ N
∴ f is invertible
∴ inverse of f exist
∴ f-1 : N → N f-1(y) = x
f-1(y) = √y .
Question 40.
If A = \(\left[ \begin{matrix} 1 & 2 & 3 \\ 3 & -2 & 1 \\ 4 & 2 & 1 \end{matrix} \right]\) then show that A3 – 23 A – 40 I = 0
Answer:


Question 41.
Solve the system of linear equation using matrix method,
x – y + 2z = 7
3x + 4y – 5z = -5
2x – y + 3z = 12
Answer:
The given system of equation can be expressed as AX = B, where
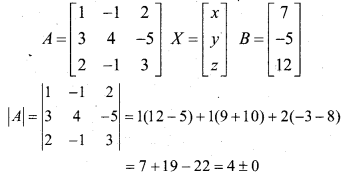
∴ A is non-singular matrix so A-1 exists.
A11 = 7, A12 = -19, A13 =-11, A21 =1, A22= -1, A23 = -1, A31 = -3, A32 = 11, A33 = 7.
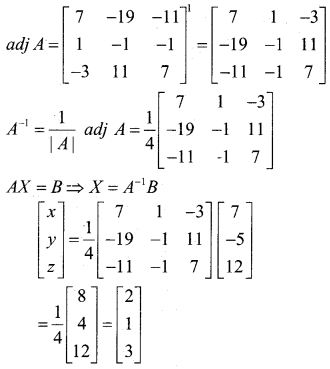
on equating, we get x = 2, y = 1, z = 3
![]()
Question 42.
Given y = 3 cos (logx) + 4 sin (logx).
x2y2 + xy1 + y = 0
Answer:
y = 3 cos (logx) + 4 sin (logx)
Diff w.r.t x
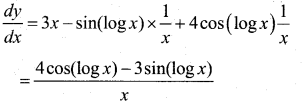

Question 43.
The length x of a rectangle is decreasing at the rate 5 cm/min and width y is increasing at the rate of 4cm/ min when x = 8cm and y = 6cm. Find the rate of change of (i) The perimeter (ii) The rate of the rectangle.
Answer:
Given \(\frac{d x}{d t}\) = -5 cm /min and \(\frac{d y}{d t}\) = 4 cm /min
a) perimeter = 2(x+ 5) ⇒ P = 2 (x + 4)
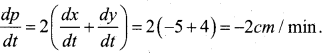
b) A Area of.rectangle = xy
⇒ A = x.y
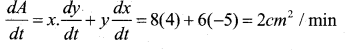
Question 44.
Find the integral of \(\frac{1}{\sqrt{x^{2}+a^{2}}^{2}}\) with respect to x and hence. Evaluate \(\int \frac{1}{\sqrt{x^{2}+7}} \cdot d x\)
Answer:
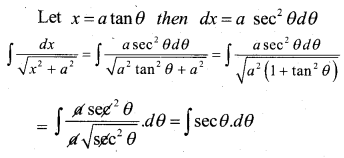

Question 45.
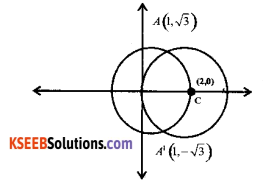
Find the area of the region enclosed b/w the two Θles. x2 + y2 = 4 and (x – 2)2 + y2 = 4
Answer:
Equations of the given circles are
x2 + y2 = 4 …………….. (1)
(x – 2)2 + y2 = 4 …………………….(2)
Equation (1) is a circle with centre O at the origin and radius 2. Eqn. (2) is a circle with centre C (2,0) and radius 2. Solving Eqn. (1) and (2), we have.
(x – 2 )2 + y2 = x2 + y2
x2 – 4x + 4 + y2 = x2 + y2
+ 4x = -4 ⇒ x = 1
x = 1 which given y = ± √3
Thus the points of intersection of the given circles are A(1,√3) and A1( 1,-√3} as shown in the fig.
Required area of the enclosed region OACA1O between circle s =2 [area of the region ODCAO]
=2 [area of the region ODAO + area of the region on DCAD]
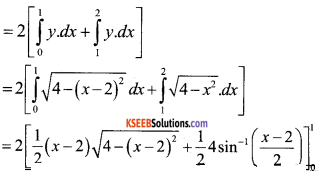

![]()
Question 46.
Solve \((x \log x) \frac{d y}{d x}+y=\frac{2}{x}(\log x)\)
Answer:

Question 47.
Derive equation of a line in a space through a given point and parallel to a vector both in the vector and cartesian form.
Answer:
Let \(\vec{a}\) be the position vector of the given point A with respect to the origion O of the rectangular co-ordinate system. Let l be the line which passes through the point A and is parallel to a given vector \(\vec{b}\) Let \(\vec{r}\) be the position vector of an arbitary point P on the line.
Then \(\vec{AP}\) is parallel to the vector \(\vec{b}\) i.e. \(\overrightarrow {A P}=\lambda \vec{b}\) where λ is some real number.
But \(\overrightarrow{A P}=\overrightarrow{O P}-\overrightarrow{O A}\)
\(\lambda \vec{b}=\vec{r}-\vec{a}\)
Conversely for each value of the parameter λ, this equation gives the position vector of a point P on the line.
Hence the vector equantion of the line is given by
\(\vec{r}=\vec{a}+\lambda \vec{b}\)
Derivation of cartesian form from vector form.
Let the co-ordinates of the given point A be (x, y, z) and the direction ratios of the line a b c consider the co-ordinates of any point P be (x,y,z) then
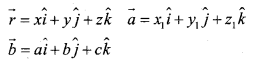
Substituting these values in (1) and equating the co-efficients i, \(\hat{i}\) and \(\hat{r}\) we get
x = x1 + λa ; y = y1 + λb ; z = z1 + λc ,
These are parametric equation of the line. Eliminating the Parameter λ from (2) we get
![]()
This is the cartesian equating of the line.
Question 48.
If a fair coins is tossed 10 times. Find the probability of
(i) Exactly six heads and
(ii) at least six heads.
Answer:
The repeated toss of a coin are Bernoullis trial s. Let X denote the number of heads in the experiment of 10 trials.
Clearly, X has the binomial distribution with
n = 10 and P = \(\frac{1}{2}\)
∴ P(X = x) = nCxqn-x – px. x = 1,2,3 ……………….. n
n = 10 and P = \(\frac{1}{2}\) q = 1 – p = \(\frac{1}{2}\)
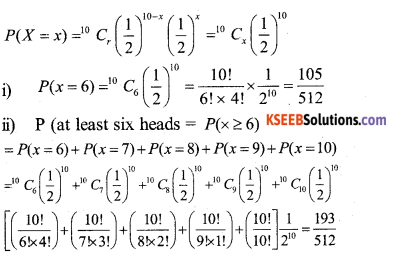
Part – E
V. Answer any One question :
Question 49.
a) Prove that \(\int_{a}^{b} f(x) \cdot d x=\int_{a}^{b} f(a+b-x) d x\) and hence. Evaluate \(\int_{\pi / 3}^{\pi / 3} \frac{1}{1+\sqrt{\tan x}} d x\)
Answer:
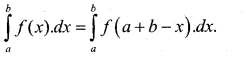
Let t = a + b – x then dt – dx
When x = a and x = b
t = b t = a

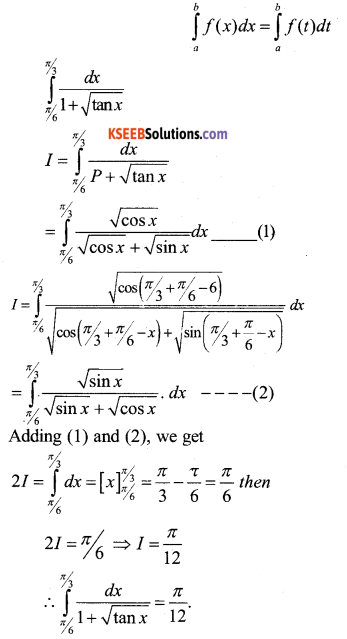
(b) Determine the value of k, if
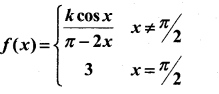
is continuous x = \(\pi / 2\)
Answer:
If f is continuous at x = \(\pi / 2\)
⇒ \(\lim _{x \rightarrow \pi / 2} f(x)=f(\pi / 2)\)
Given at x = \(\pi / 2\)
f( \(\pi / 2\) ) = 3

![]()
Question 50.
a) Minimize and maximize
Z = 5x + 10y
subject to the constraints
x + 2y ≤ 120
x + y ≥ 60,
x – 2y ≥ and x ≥ 0, y ≥ 0 by graphical method.
Answer:
Given : Z = 5x + 10y ……………. (1)
subject to constraints x + 2y ≤ 120 …………….(2)
x + y > 60 …………….(3)
x – 2y ≥ 0 …………….(4)
x ≥ 0, y ≥ 0 …………….(5)
First we locate the region represented by (2), (3), (4) & (5) for this consides the lines ;
x + 2y = 120 which passes through A(120, 0) & B(0, 60)
x + y = 60 which passes through C (60, 0) & B (0, 60) and x – 2y = 0 which passes through 0 (0, 0) & P (40, 20)
Now that P(40, 20) lies on BC also. Also x – 2y = 0&x + 2y= 120 meet in Q (60, 30)
The feasible region is shown shaded in the figure (indicated as feasible region) note that (0,0) does nopt lie in this region as it doesnot satisfy (3) The point C(60,0) lie this region as it saties fies all the constraints (2) (3) (4) and (5).
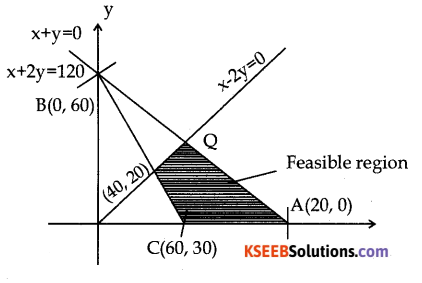
The corner points of the feasible region which are to be examined for optimum solution are C(60,0) A( 120,0) Q(60, 30) and P(40,20)
At C(60, 0), Z = 5 × 60 + 10 × 0 = 300
At A(120, 0), Z = 5 × 120 + 10 × 0 = 600
At Q(60, 30), Z = 5 × 60 + 10 × 30 = 600
At P(40, 20), Z = 5 × 40 + 10 × 20 = 400
Hence Z is minimum at C(60,0) and min Z = 300 and max Z = 600 at A and also at Q ⇒ max Z will be attained at every point of segment AQ.
b) Find the value of k, if
f(x) = \(\frac{1-\cos 2 x}{1-\cos x}\) , x≠ 0
f(x) = k ,x= 0
is continuous at x = 0.
Answer:
