2nd PUC Maths Model Question Paper 1 with Answers

Students can Download 2nd PUC Maths Model Question Paper 1 with Answers, Karnataka 2nd PUC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Model Question Paper 1 with Answers

Time: 3 Hrs 15 Min
Max. Marks: 100

Instructions:

1. The question paper has five parts namely A, B, C, D and E. Answer all the parts.
2. Use the graph sheet for the question on Linear programming in PART E.

Part – A

I. Answer all the following questions ( 10 x 1 = 10 )

Question 1.
Give an example of a relation which is reflexive and symmetric but not transitive.
Answer:
R = {(1,2),(2,3),(2,1),(1,3), (3,2)}

Question 2.
Find the value of cot (tan^-1 x + cot^-1 x)
Answer:
cot ( tan ^-1 x cot ^-1 x = cot ( \(\frac{\pi}{2}\) ) = 0

Question 3.
Define a scalar matrix.
A diagoral matrix is said to be a scalar if the principal diagoral are same.

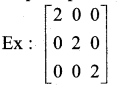
Question 4.
If
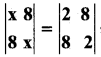, find the values of x.
Answer:

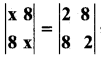
⇒ x² – 64 = 4 – 64
⇒ x² = 4
⇒ x = ±2

Question 5.
Differentiate sin √X with respect to x
Answer:

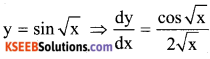
Question 6.
Evaluate : ∫ \(\frac{1-x}{\sqrt{x}} d x\)
Answer:

Question 7.
Find the vector components of the vector with initial point {2,1} and terminal point (-5, 7)
Answer:

Question 8.
What is the equation of the plane that cuts the coordinate axes at (a, 0,0), (0, b, 0) and (0, 0, c)
Answer:
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)

Question 9.
Define the term corner point in the L.p.p
Answer:
A comer point of a feasible region is a point in the region which is the intersection of the two boundary lines.

Question 10.
If E is an event of a sample space S of an experiment then find P(SIF)
Answer:
P(S/F) = \(\frac{\mathrm{P}(\mathrm{SnF})}{\mathrm{P}(\mathrm{F})}\)

Part -B

Answer any Ten questions: ( 10 x 2 = 20 )

Question 11.
Verify whether the operation * defined on Q by a*b = \(\frac{\mathrm{ab}}{4}\) is associative or not.
Answer:
a*b = \(\frac{\mathrm{ab}}{4}\)

from 1 and 2
(a*b)*c = a*(b*c)
⇒ * is associative

Question 12.
Find the value of tan^-1(√3) -sec^–(-2)
Answer:
tan^-1(√3) -sec^–(-2)

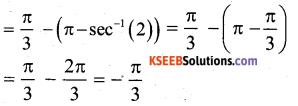
Question 13.
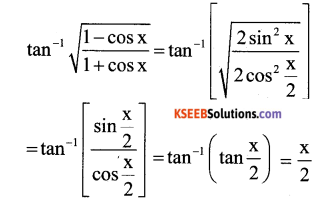
Write the simplest form of \(\tan ^{-1}(\sqrt{\frac{1-\cos x}{1+\cos x}})\) , 0 < x < π

Question 14.
Let A(1, 3), B(0, 0) and C(K, 0) be the vertices of triangle ABC of area 3 sq. units. Find k using determinant method.
Answer:

A = \(\frac { 1 }{ 2 }\) [1(0 – 0) – 3(0 – K) + 1(0 – 0)
A = \(\frac { 1 }{ 2 }\)[3K]
Given , Area = 3 sq. units,
Thus- \(\frac { 3k }{ 2 }\) = +3 \(\frac { 3k }{ 2 }\) = -3
⇒ 3k = 6, 3k = -6
k = 2, k = -2

Question 15.
Prove that greatest integer function defined by f(x) = [x], 0<<3 is not differentiable at x = 1
Answer:
Since fis not continuous at every Integral
point or at x= I
⇒ It follows that [x] cannot differentiate at x = 3.

Question 16.
Find \(\frac{\mathrm{d} y}{\mathrm{d} x}\) ,If x 4t and y = \(\frac{4}{t}\)
Answer:
x = 4t \(\frac{\mathrm{d} x}{\mathrm{d} x}\) = 4
y = \(\frac{4}{t}\) \(\frac{\mathrm{d} y}{\mathrm{d} x}\) = \(\frac{-4}{t^{2}}\)

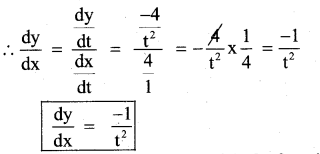
Question 17.
Find the intervals in which the function fgivenby f(x) = x² – 4x + 6 is strictly increasing.
Answer:
f(x) = x² – 4x +6
f¹ (x) = 2x -4
f¹ (x ) =0 given, 2x – 4=0 ⇒ 2x =4
⇒ x = 2
Thus f¹(x ) =0 at x =2
Now, the point x = 2 divides the real line
into two disjoint intervals namely,
(-∞,2) and (2,∞).
At (2,∞),f¹ (x) > 0
⇒ f is strictly increasing at(2,∞)

Question 18.
Evaluate : ∫sin3x.cos4xdx
Answer:
Let I = ∫ sin 3x.cos 4x dx
USE:
sin A. cos B = \(\frac{1}{2}\) [sin(A + B)+sin(A + B)]
= \(\frac{1}{2}\)∫ [sin(3x + 4x) + sin(3x – 4x)J dx
= \(\frac{1}{2}\)∫ [sin7x + sin(-x)] dx
= \(\frac{1}{2}\) ∫[sin7x + sin x] dx

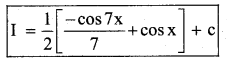
Question 19.
Evaluate : ∫logx dx.
Answer:
I = ∫logx dx = ∫logx.1 dx
= ∫uv dx =u∫v dx – ∫[\(\frac{d}{d x}\) x∫vdx] dx
Iogx ∫1. dx_∫[\(\frac{d}{d x}\) (logx)x∫1.dx] dx
=1ogx(x)∫( \(\frac{1}{x}x x\) ) dx
=xlogx – ∫1. dx
I = x logx – x + c

Question 20.
Form the differential equation of the family of curves \(\frac{x}{a}+\frac{y}{b}=1\), by eliminating the contants “a” and “b”
Answer:

Question 21.
If either \(\overrightarrow{\mathbf{a}}=\overrightarrow{\mathbf{0}}\) or then \(\mathbf{a} \cdot\overrightarrow{\mathbf{b}}=\mathbf{0}\) but the converse need not not be true. Justify your answer with an example.
Answer:

\(\overrightarrow{\mathrm{a}} . \overrightarrow{\mathrm{b}}\) = 6(4)+2(-4) + (-8)(2)
= 24 – 8 – 16
=0
=> \(\overrightarrow{\mathrm{a}}\) is Δ^r to b
Take any two non – zero perpendicular vectors \(\overrightarrow{\mathrm{a}}\) & \(\overrightarrow{\mathrm{b}}\)
Hence, the convrse need not be true

Question 22.
Find the angle θ between the vectors \(\overrightarrow{\mathbf{a}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{b}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}\)
Answer:

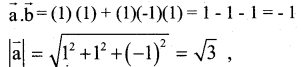
Question 23.
Find the distance between the parallel – lines
\(\vec{r}=\hat{\mathbf{i}}+2 \hat{\mathbf{j}}-4 \hat{\mathbf{k}}+\lambda(2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+6 \hat{\mathbf{k}}) and \overrightarrow{\mathbf{r}}=3 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}-5 \hat{\mathbf{k}}+\mu(2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+6 \hat{\mathbf{k}}\) )
Answer:

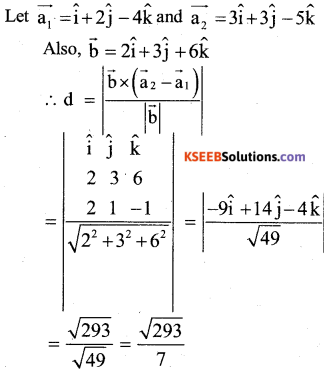
Question 24.
A fair die is rolled. Consider the events E = {1, 3, 5}, F = {2, 3} and G{2, 3, 4, 5}. Find (i) P(E/F) ii) P(E/G)
the set A = {l,2,3,4,5,6}
Answer:

Part – C

Answer any Ten Questions : ( 10 x 3 = 30 )

Question 25.
Determine whether the relation R in the set A={I,2,3,4,5,6} as R={x,y}:y is divisible by x} is reflexive, symmetric and transitive.
Answer:
(1) R is reflexive, as (a,a) ∈ R ⇒ a is
divisible by a ∴ R is reflexive.
(2) Let (1,2) ∈ R ⇒ 2 is divisible by 1
But (2,1) ∈ R ⇒ 1 cannot divide by 2
∴ R is not symmetric.
(3) Let (1,2)∈ R ⇒ 1(2, 4)ER
⇒ 2 is divisible by I and 4 is divisibly by 2
Now, (1,4) ∈ R ⇒ 4 is divisible by 1
∴  (1,2)∈ R I(2,4) ∈ R ⇒ (1,4)∈ R
∴ R is transitive.

Question 26.
Find the values of x, if

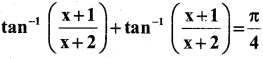
Answer:

⇒x² = 4 – 3 = 1
∴ x = ±1

Question 27.
Answer:
Find the values of x and y.
Answer:

Question 28.
If y^x + x^y = a^b, find \(\frac{d y}{d x}\)
y^x + x^y = a^b …..(1)
‘ Let u = y^x and v = x^y

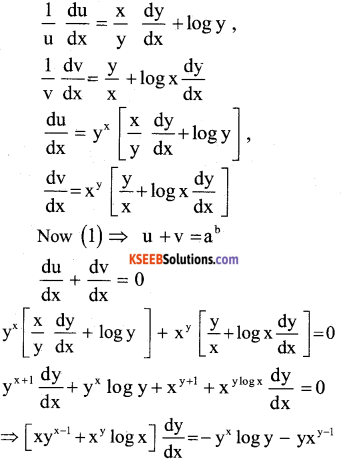
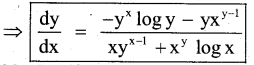
Question 29.
Verify Mean value theorem for the
function f(x) = x³ – 5x² – 3x , in the interval[a,b] where a= 1 and b = 3
(1) f(x) = x³ – 5x² – 3x is continuous in [1,3]
(2) f¹(x) = 3x² – 10x – 3 exists in [1, 3]

3c² – 10c – 3 +10 = 0
3c² – 10c + 7 = 0
= 3c² – 3c – 7c + 7 = 0
= 3c (c – 1) – 7 (c – 1) = 0
=(3c – 7) ((c- 1)) = 0
c = \(\frac{7}{3}\) or c=1
But c ∉ (1,3) ∴c = \(=\frac{7}{3}\)∈ (1 , 3 )

Question 30.
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Answer:
Let one number be x. Then other number is (16 – x)
Let S(x) = x³ +(16 – x)³
S¹ (x) = 3x² +3(16 – x)² (-1)
S¹¹(x) =6x + 6(16 -x)¹(+1)
S¹(x) = 0 gives, 3x² – 3 (16 – x)² =0
⇒ x² – (16 – x)² =0
⇒ x² = (16 – x)²
⇒ x² – 256 + x² – 32x
⇒ 32x = 256
x = \(\frac{256}{32}\)
x =8
Also, S¹¹ (x) = 6(8)+ 6(16 – 8)
= 48 + 6(8)
= 48 + 48
= 96 > 0
∴ By second derivative test, x = 8 is the point of local minima of s.
Hence sum of cubes of numbers is
minimum when the numbers are 8 and 16-8 = 8

Question 31.
Find ∫\(\frac{x}{(x+1)(x+2)} d x\)
Answer:
Let I = \(\frac{x}{(x+1)(x+2)} d x\)
Resolve into partial fractions,

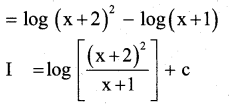
Question 32.
Evaluate ∫\(\frac{1}{1+\tan x} d x\)
Answer:

Question 33.
Find the area of the region bounded by the curve y = x² and the line y=4
Answer:

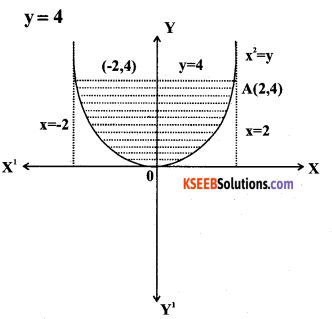
Given y = x² and y = 4
To find A and B:
put y = 4 in y = x²
⇒ x² = 4
⇒ x =±2
put x = 2, y = 4 ⇒(2,4)
x = -2, y = 4 ⇒ (-2,4)

Question 34.
Prove that the equation
x²\(\frac{d y}{d x}\) = x² – 2y² + xy is a homogeneous differential equation.
Answer:
x²\(\frac{d y}{d x}\) = x² – 2y² + xy

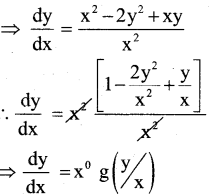
:. (1) is homogeneous DiffentiaI Equation.

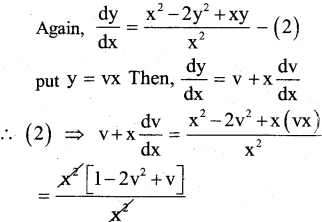
Question 35.
Find a vector perpendicular to each of the vectors \(\overrightarrow{\mathbf{a}}=2\) \(\hat{\mathbf{i}}+\hat{\mathbf{j}}+3 \hat{\mathbf{k}}\)
\(\overrightarrow{\mathbf{b}}=3 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}+2 \hat{\mathbf{k}}\) which has magnitude 10 units.
Answer:
Let \(\overrightarrow{\mathbf{a}}=2\) \(\hat{\mathbf{i}}+\hat{\mathbf{j}}+3 \hat{\mathbf{k}}\) and
\(\overrightarrow{\mathbf{b}}=3 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}+2 \hat{\mathbf{k}}\)

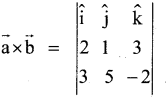
= î[- 2 – 15] – ĵ[-4 – 9] + k̂[10 – 3]
= î[-17] – ĵ [-13] + k̂[7]
= -17î + 13 ĵ + 7k̂

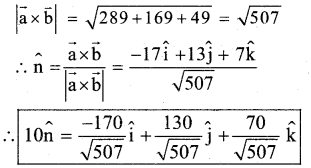
Question 36.
Show that the points and A (-1, 4, -3), B(3,2,-5) C (-3,8,-5) D(-3,2,1)are coplanar.
Answer:
\(\overrightarrow{\mathrm{AB}}=4 \hat{\mathrm{i}}+(-2) \hat{\mathrm{j}}+(-2) \hat{\mathrm{k}}\)
\(\overrightarrow{\mathrm{BC}}=-6 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}+0 \hat{\mathrm{k}}\)
\(\overrightarrow{\mathrm{CD}}=0 \hat{\mathrm{i}}-6 \hat{\mathrm{j}}+6 \hat{\mathrm{k}}\)

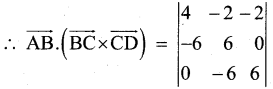
= 4[36 + 0] + 2 [- 36 – o] – 2[36 – 0]
= 144 – 72 – 72 = 144 – 144 = 0
∴ A, B, C & D arc coplanar.

Question 37.
Find the cartesian and vector equation of the line that passes through the points (3,-2,-5) and (3,-2,6)
Answer;

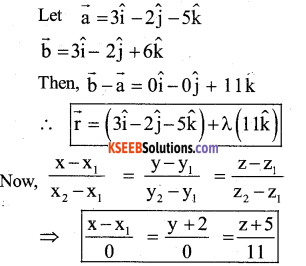
Question 38.
A die is thrown. If E is the event “the number appearing is a multiple of 3” and F be the event “The number appearing is even”. Then find whether E and F are independent
Answer:
s = {1,2,3,4,5,6}
E={3,6} ∴P(E) = \(\frac{2}{6}=\frac{1}{3}\)
F={2,4,6} ∴ P(F) = \(\frac{3}{6}=\frac{1}{2}\)
we have, P(EnF) = P(E)P(F)
\(\frac{1}{6}\) = \(\frac{1}{3} x \frac{1}{2}\)
\(\frac{1}{6}\) = \(\frac{1}{6}\)
∴ E and F are Independent

Part – D

Answer any sir auestinns: ( 6 x 5 = 30 )

Question 39.
If f:A → A defined by f(x) = \(\frac{4 x+3}{6 x-4}\) where A = R{ \(\frac{2}{3}\) }
show that is invertible and f ^-1 = f.
Answer:

Question 40.
If
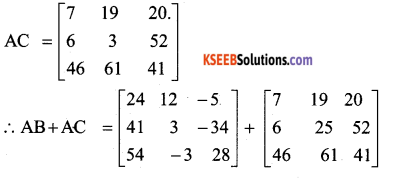
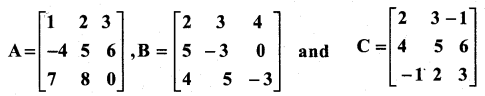, Prove that A(B + C) = AB + AC.
Answer:

Question 41.
Solve the following system of equation by
method:x + 2y + 3z = 2; 2x + 3y + z = -1 and x – y – z = -2
Answer:
Consider A x B → (1) ⇒ x = A^-1 B – (2)

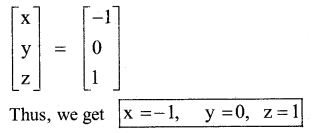
Question 42.
ir y = (tan^-1x)², prove that
(x² +1)² y₂ + 2x(x² +1)y₁ =2
Answer:
y = (tan^-1x)²

Question 43.
A particle moves along the curve 6y=x³ + 2. Find the points on the curve at which the y – coordinate is changing 8 time as fast as the x- coordinate.
Answer:
6y = x³+2 ……… (1)

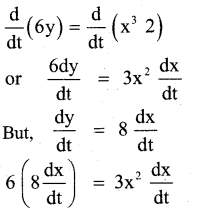
(or) 3x² = 48
(or) x² = 16
∴ x = ±4
from (1): y = 11 and Y = \(\frac{31}{3}\)
Hence , the required points are (4 , 11) and (-4, \(\frac{-31}{3}\))

Question 44.
Find the integral of \(\frac{1}{\sqrt{\mathbf{a}^{2}-\mathbf{x}^{2}}}\) with respect to x, and hence evaluate \(\int \frac{d x}{\sqrt{5-4 x-x^{2}}}\)
Answer:
Let I = ∫\(\frac{1}{\sqrt{a^{2}-x^{2}}} dx\) -(1)
Put x = a sin θ (or) θ = sin ^-1 ( \(\frac{x}{a}\) )
Then dx = a cosθ dθ

Question 45.
Find the area of the of the circle x² + y² = a² by the method of the integration and hence find the area of the circle x² + y² = 2.
Answer:

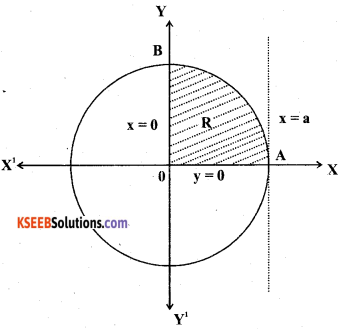
Question 46.
Find the general solution of the differential equation
\(\frac{d y}{d x}\) + y.cotx = 2x + x².cotx
\(\frac{d y}{d x}\) + y.cotx = 2x + x² .cotx
Let P = cot x, Q = 2x + x²cot x
I.F = e^∫pdx = e^∫cotxdx = e∫^{log(sin x )} = sin x
Sol is
y (I.F) = ∫ (QxI.F) dx +C
y sinx = ∫(2x + x²cotx)sin dx + c
= ∫(2x + x2 cotx) dx +c
=2 ∫ x sin xdx + ∫x² cosx dx + c
= 2[x(-cosx)-(1)(-sinx)] +[x² sinx – 2x(-cosx) + 2c(-sinx)]
=2xcos x+2sin x +x²sinx
y sin x = x² sinx + c

This is the Required General solution for the given differential Equation.

Question 47.
Derive the formula to find the shortest distance between the two skew lines \(\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{a}}_{1}+\lambda \overrightarrow{\mathbf{b}}_{1}\) and
\(\overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{a}}_{2}+\mu \overrightarrow{\mathbf{b}}_{2}\) in the vector form.
Answer:

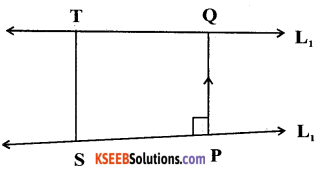
(1) Let \(\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}_{1}+\lambda \overrightarrow{\mathrm{b}}_{1}\) and \(\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{a}}_{2}+\mu \overrightarrow{\mathrm{b}}_{2}\) be two skew lines.
(2) Take any point S on l₁, with posotion vector \(\overrightarrow{\mathrm{a}}_{1}\) and T on l₂ with the position vector \(\overrightarrow{\mathrm{a}}_{2}\)
(3) clearly \(\overrightarrow{\mathrm{PQ}}=\mathrm{d} \hat{\mathrm{n}}\) where \(\hat{n}=\frac{\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{b}}_{2}}{\left|\overrightarrow{\mathrm{b}}_{1} \times \overrightarrow{\mathrm{b}}_{2}\right|}\)
where, d – shortest distance
\(\hat{n}\) – units Normal vector
(4) Let θ be angle between \(\overrightarrow{\mathrm{PQ}} and \overrightarrow{\mathrm{ST}}\)
Then, PQ = ST|COSθ| — (1)
(5) But,

This is the required shortest Distance between two skew lines.

Question 48.
A fair coin is tossed 8 times. Find the probability of at most 5 Heads.
Answer:
Let p = probability of getting head = \(\frac{1}{2}\)
q = Probability of getting tail = \(\frac{1}{2}\)
n = 8

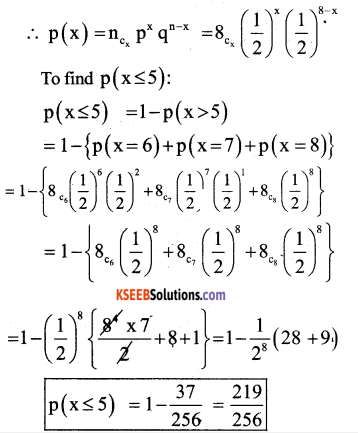
Part – E

Answer any one question: ( 1 x 10 = 10 )

Question 49.
(a). A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs7.OO per package on bolts. How many packages of each should be produced each day so as to maximize his profit if he operates his machines for at the most 12 hours a day?
Let x → nuts, y → bolts

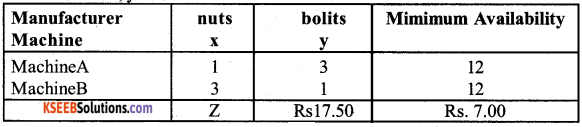
Maximimum: Z = Rs. 17.50 x + Rs 7.00 y
x + 3 ≤ 1 2
3x + y ≤ 12 where, xy ≥ 0

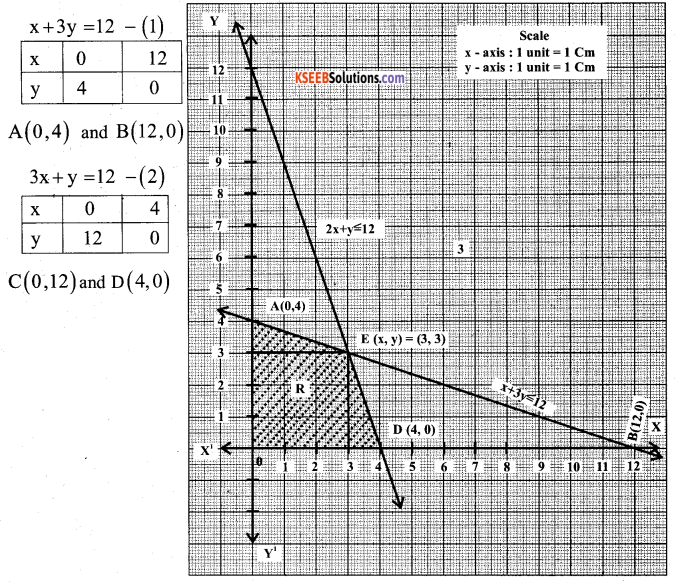
The shaded portion OAED Represents feasible region and it is bounded.
The feasible solution is obtained at all these comer points.

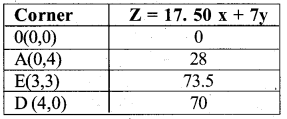
∴ (z)_max =73.5atx =3 andy =3.
Thus the manufactures gets maximum prom 01 KS ,j.5 on producing 3 packets of nuts and 3 packets of bolts.

(b).

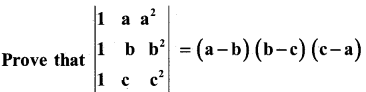
Answer:


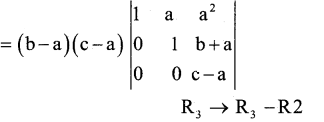
On Expanding along c₁
= (b – a) (c – a) {1[(- b)] J
= (b – a) (c – a) (c – b)
= (a – b) (b – c) (c – a)
= RHS

Question 50.
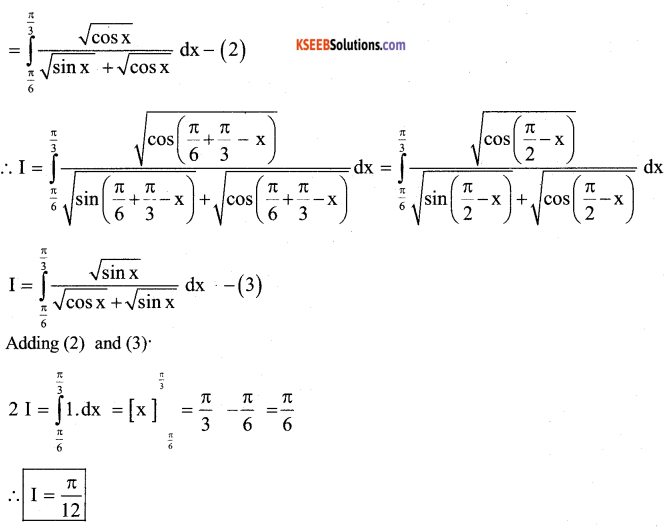
(a) Prove that \(\int_{2}^{b} f(x) d x=\int_{a}^{b} f(a+b-x) d x\) and hence evaluate \(\int_{\frac{\pi}{3}}^{\frac{\pi}{3}} \frac{\mathrm{dx}}{1+\sqrt{\tan x}}\)
Answer:
Let t = a + b – x. Then dt = -dx
when x = a, t = b
and x = b, t=a

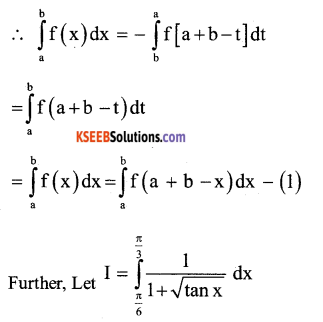
(b). Find all the points of discontinuity on f defined by f(x) =|x| – |x+1|
Answer:
f(x) = |x| – |x+1|
f(c)= |c | – |c+1|
Let c = O, f(0) = |0 |-|1| = 0-1= -1
Lt f(x) = It|x| – |x+1|= |c| – |c+1|
x→ c X → C
let c = 0, Lt f(x)=0 – 1 = – 1
x—+0
∴ \(\underset{x \rightarrow 0}{\mathrm{Lt}}\) f(x) = f(0)=-1
⇒ f is continuous at x =0
There is no point of Discontinuity.