2nd PUC Biology Model Question Paper 3 with Answers

Students can Download 2nd PUC Biology Model Question Paper 3 with Answers, Karnataka 2nd PUC Biology Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Biology Model Question Paper 3 with Answers

Time: 3.15 Hours
Max Marks: 70

General Instructions:

1. This question paper consists of four parts A, B, C and D. Part D consists of two parts, Section – I and Section – II.
2. All the parts are Compulsory.
3. Draw diagrams wherever necessary. Unlabelled diagrams or illustrations do not attract any marks.

Part – A

I. Answer the following questions in One Word or One Sentence each : ( 10 × 1 = 10 )

Question 1.
Name the site of fertilization in female human beings.
Answer:
Upper limb (Ampullary – isthmic junction) of fallopian tube.

Question 2.
Define adaptive radiation
Answer:
It is the evolution of different animals in different direction from a common ancestor adapting to different ecological niches. It is also called as divergent evolution.

Question 3.
Name the organism that causes typhoid.
Answer:
Salmonella typhi.

Question 4.
What is green revolution?
Answer:
The dramatic increase in food production due to improvement of high yielding and disease resistant crop varieties is called green revolution.

Question 5.
Name the microbe that causes big holes in the Swiss cheese.
Answer:
Propioni bacterium sharmanii

Question 6.
Why does the logistic growth curve becomes S shaped?
Answer:
In sigmoid growth unlimited resources are rare, population growth is, therefore becomes stable due to environmental resistance.

Question 7.
Breast feeding during the initial period of infant growth is recommended. Give reason?
Answer:
The yellowish milk (colostrum) secreted from mammary glands during the initial days contains antibodies (IgA) to boost the development of immune system of the child.

Question 8.
Give an example for chemical carcinogen that causes cancer.
Answer:
Alcohol or tobacco or coal tar or coal gas or asbestos cement etc

Question 9.
What is totipotency?
Answer:
The capacity to generate a whole plant from any cell or explant is called totipotency

Question 10.
How do birds cope with temporary fluctuations in their environmental conditions?
Answer:
They migrate to hospitable areas for food and breeding purposes during unfavourable conditions in their habitat.

Part – B

II. Answer any FIVE of the following questions in 3 – 5 sentences each, wherever applicable : ( 5 × 2 = 10 )

Question 11.
Name the plant that shows unusual flowering phenomenon in hilly tracks of Karnataka, Kerala and Tamilnad.
Answer:
Strobilanthus kuluthiana ( Neelakuranji)

Question 12.
What is Biochemical Oxygen Demand (BOD)? Mention its significance.
Answer:
BOD refers to the amount of oxygen that would be consumed if all the organic matter in one liter of water were oxidized by bacteria.

Significance

• The BOD test measures the rate of uptake of oxygen by micro-organisms in a sample of water.
• Indirectly BOD is a measure of the organic matter present in the water.
• The greater the BOD of waste water more is its polluting potential.

Question 13.
Differentiate test cross and out cross.
Answer:
Test cross
It is a cross between F₁ hybrid and homozygous recessive parent.

Out cross
It is a cross between F₁ hybrid and homozygous dominant parent.

Question 14.
Give two examples for natural selection in organisms.
Answer:

1. Industrial melanism in Biston betularia
2. Antibiotic resistance in bacteria

Question 15.
What are single cell proteins? Mention their importance?
Answer:
Dried biomass of a single species of microbes that can be used as protein source in the diet is known a single cell protein (SCP).

Single cell proteins (SCP) are alternative source of proteins used to feed the ever increasing population with protein rich diet to overcome the problems of protein malnutrition.

Question 16.
Why is India said to have greater ecosystem diversity than Norway?
Answer:
India with diverse ecosystems such as rain forests, coral reefs, wet lands, coastal areas, mangroves, estuaries and deserts has greater ecosystem diversity than Norway.

Question 17.
Draw a diagram of sparged tank bioreactor and label the parts.
Answer:

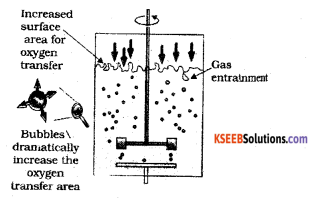
Question 18.
Explain the mechanism of action of restriction endonucleases.
Answer:
Restriction endonucleases recognize a specific base sequence of a DNA molecule.
They cut double stranded DNA at different sites. This generates protruding (51 or 31) ends. Such ends are called cohesive or sticky ends. These ends can join with single stranded sequences of other DNA having complementary base pairs.
E.g. EcoRI, Bam H1

Cuts symmetrically placed around the line of symmetry

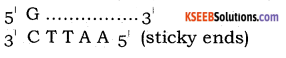
Part – C

III. Answer any FIVE of the following Questions in 40-80 words each, wherever applicable. ( 5 × 3 = 15 )

Question 19.
Describe the different phases of life cycle.
Answer:
Juvenile phase
The period of growth from birth till individual attains sexual maturity is called Juvenile phase. It is known as vegetative phase in plants.

Reproductive phase
The period of growth after Juvenile or vegetative phase during which individual reaches sexual maturity and capable of producing gametes is called reproductive phase. In human beings reproductive phase begins on the onset of puberty usually after 13 or 14 years. In plants flowering marks the beginning of reproductive phase.

Senescent phase
The phase begins after reproductive phase and marks the end of growth cycle in organisms.

Question 20.
Give a brief account of Human Origin and evolution.
Answer:

• Human evolution states that humans developed from primate or ape like ancestors.
• Human origin occurred in Central Asia and Africa, China, Java and India (Shivalik hills).
• The first mammals were shrew like terrestrial, insectivores or rat like creatures.
• The insectivorous mammals namely tree shrews gave rise to the primitive primates called prosomians which include tarsiers, lemurs and lories and anthropoids (marmosets, baboons, monkeys, apes and man).
• Modem man Homo sapiens belongs to class mammalia, order primata and suborder anthropoidea.
• Dryopithecus africanus is regarded as common ancestor of man and apes.
• It is lived about 20 – 25 million years ago (Miocene).
• Dryopithecus gave rise to Rama pithecus; he appeared 14-15 million years ago.
• The fossil of Rama pithecus was discovered from Pliocene rocks of Shivalik hills of India by Edward Lewis.
• Rama pithecus gave rise to Australo pithecus after a gap of 9 – 10 million years.
• Rama pithecus the first ape man commonly called southern ape .He appeared about 5 million years ago (early Pleistocene).
• Homo habillus lived in early Pleistocene about 2 million years ago.
• He was the first tool maker or handy man.
• Homo erectus is the direct ancestor of modern man.
• Homo erectus evolved from homo habillus about 1-7 million years ago in middle Pleistocene.
• Homo erectus include Java ape man, pieking man and Heidelberg man.
• The Neanderthal man existed in the late Pleistocene he was roughly equal to the modem man.
• Cro-Magnon is regarded as direct and most recent ancestor of the living modem man.
• He lived about 34.0000 years ago in Holocene epoch.
• The cranial capacity was about 1650cc and considered more intelligent than the man of today.
• The modern man Homo sapiens arose in Africa about 25.0000 years ago in Holocene epoch.
• It is believed that the man of today appeared about 11.000 or 10.000 years ago in the region around Caspian and Mediterranean seas from their members migrated west wards, eastwards and south wards respectively changing into present day white or Caucasoid, Monogoloid and black or Negroid races.
• Modern man underwent cultural evolution. Cave art developed about 18.000 years ago.
• Agriculture came around 10.000 years back and human settlement started.

Question 21.
List the various public health measures as a safeguard against infectious diseases?
Answer:
Following are the public health measures, considered safe against infectious diseases.

1. Maintenance of personal and public hygiene like proper disposal of waste and excreta through proper sanitation.
2. Provision of safe water supply, periodic cleaning and disinfection of water reservoirs, pools, and tanks, etc.
3. Standard practices of hygiene in public health catering.
4. Avoiding stagnation of water in and around residential areas to prevent breeding of mosquitoes and vectors.
5. Spraying of insecticides like DDT in ditches, drainage areas, swamps, etc., to prevent mosquito breeding.
6. Measures against vector borne diseases like dengue and chikungunya, include fixing of wire meshes to doors and windows to prevent the entry of mosquitoes.
7. Regular health camps, immunization (Vaccination) programmes to prevent the spread of infectious diseases.

Question 22.
What is food chain? Describe the types of food chain.
Answer:
The transfer of food energy from producers to decomposers through a series of organisms with repeated eating and being eaten is called food chain.
1. Grazing food chain
The food chain begins with producers (green plants) at the first trophic level. It involves grazing Of grass by herbivores and flow of energy occurs from smaller organisms (herbivores) to larger animals (consumers). It is based on prey – predator relationship and is therefore, called predator food chain.
Grass → Deer → Tiger

2. Parasitic food chain
The food chain begins with producers and flow of energy goes from larger organisms (host) to smaller organisms (parasites) as parasites draw nourishment from the host. This is based on host – parasite relationship.

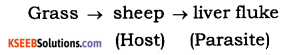
3. Detritus or saprophytic food chain
The food chain begins with dead and decaying organic matter (detritus). Which is acted upon by decomposers or saprophytes and energy from decomposers goes to detrivores.
Leaf litter → Earth worm → bird → hawk

Question 23.
Define the terms
(a) Emasculation
Answer:
The removal of anthers from the flower bud of a bisexual flower before the anther dehisces is called emasculation.

(b) Bagging
Answer:
The process of covering the emasculated flowers with a bag of suitable size to prevent contamination with unwanted pollen is called bagging.

Question 24.
What is transformation? Explain any two methods of introduction of recombinant DNA in to host organism.
Answer:
Transformation is the process by which plasmid or DNA can be introduced into a cell.

1. Gene gun or particle gun or Biolistics method
It is a popular and widely used direct gene transfer method for delivering foreign genes into any cells and tissues or even intact seedlings.

• The foreign DNA is coated or precipitated onto the surface of minute gold or tungsten particles (1-3 pm).
• It is bombarded or shot onto the target tissue or cells using the gene gun or micro projectile gun or shot gun.with a device much like a particle gun. Hence the term biolistics
• The bombarded cells or tissues are cultured on selection medium to regenerate plants from the transformed cells.

2. Micro injection
In this technique a solution of DNA is directly injected in to the host nucleus using a fine micro capillary pipette or micro syringe, under a phase contrast microscope to aid vision.

Question 25.
Define trophic level. Show schematically the different tropic levels in a food chain.
Answer:
The amount of energy available at each step in food chain is called Trophic level.

Question 26.
What is pedigree? Show diagrammatic representation of pedigree for sickle cell anemia.
Answer:
Pedigree is a chart of graphic representation of record of inheritance of a trait through several generations in a family

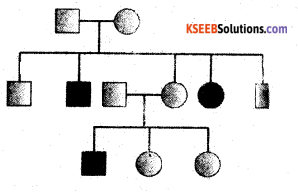
Part – D

Section – I

IV. Answer any FOUR of the following questions on 200 – 250 words each, wherever applicable . ( 4 × 5 = 20 )

Question 27.
What are assisted reproductive technologies? Describe the various reproductive technologies to assist an infertile Couple to have children.
Answer:
The couple can be assisted to have children through certain special techniques known as assisted reproductive technologies (ART).
1. In vitro fertilization and embryo transfer (IVF-ET)

• In this technique egg cells are fertilized by sperm (usually 100,000 sperm / ml) outside the body in almost similar conditions as that in the body.
• In this process Ova from the wife or donor female and sperm from husband or donor male are allowed to fuse in shallow containers called Petri dishes. (Made of glass or plastic resins) Under laboratory condition.
• The fertilized egg (zygote) is then transferred to the patient’s uterus this called embryo transfer (E.T.), Where she provides suitable conditions for the development of embryo.
• The baby born by this technique is called test tube baby.

2. ZIFT ( Zygote intra fallopian transfer)
Zygote or early embryo up to eight blastomeres is transferred into the fallopian tube.

3. Gamete intra fallopian transfer (GIFT)
Transfer of an ovum collected from a donor to fallopian tube of another female who cannot produce ova, but provide suitable conditions for fertilization and further development up to parturition.

4. Intra uterine transfer (IUT)
Embryo with more than eight blastomeres is transferred in to the uterus.

5. Intra cytoplasmic sperm injection (ICSI)
The sperm is directly injected into the cytoplasm of the ovum to form an embryo in the laboratory and then embryo transfer is carried out.

6. Artificial insemination (AI)

• This method is used in cases where infertility is due to the inability of the male partner to inseminate the female or due to very low sperm counts in the ejaculates.
• In this method, the semen collected from the husband or a healthy donor is artificially introduced into the vagina or into the uterus (IUI – Intra uterine insemination).

Question 28.
What is dihybrid cross? State and explain Mendel’s second law of independent assortment.
Answer:
When a cross is made between two parents differing in two pairs of contrasting characters like round yellow and wrinkled green is called dihybrid cross.

Based on the results obtained from dihybrid cross, Mendel postulated his second law “The law of independent assortment”. It states that, when two pairs of contrasting characters are brought into the hybrid they behave independently of each other without contamination. The presence of one character is not contaminated with the other character. These characters are assorted independently of one another during the formation of gametes.
Mendel conducted dihybrid cross for which he selected two characters at a time.

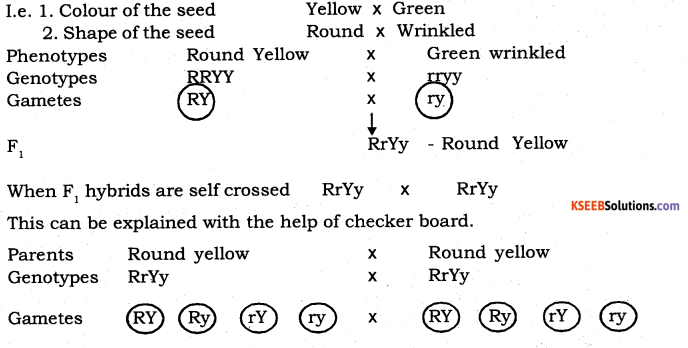
Self crossed (F2)

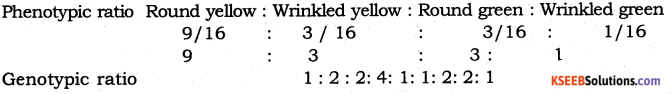
Question 29.
What is meant by semi conservative replication? How did Meselson and Stahl prove it experimentally?
Answer:

It is a process by which DNA produces daughter DNA molecules, which are exact copies of the original DNA. In each new DNA molecule, one strand is old (original) while the other is newly formed. Hence, Watson and Crick described this method as semi-conservative replication.

Meselson and Stahl conducted experiments on E.coli to prove that DNA replication is semi conservative.

1. They grew E.coli cells in a culture medium containing radioactive isotopes N¹⁵ (NH₄cl).
   The ¹⁵N was incorporated into the newly synthesized DNA and other nitrogen containing compounds.
2. Bacteria labeled with ¹⁵N are transferred into a medium containing normal ¹⁴NH₄cl.
3. The analysis was done after every generation at regular intervals.
4. The DNA samples were separated by centrifugation on CSCl₂ gradient.
5. The hybrid DNA separated from fresh generations possesses one heavier strand contributed by parental with ¹⁵N isotope which is radioactive and lighter strand is newly synthesized with ¹⁴N isotope, is non-radioactive.
6. The DNA of the second generation showed that in one DNA molecule one strand was radioactive (¹⁵N) and other was non radioactive (¹⁴N), Whereas both the strands of other DNA molecule were non-radioactive (¹⁴N).
7. It is clear that the DNA of the first generation is intermediate it contains both ¹⁵N and ¹⁴N.
8. In the second generation there were two types of DNA one heavier DNA with ¹⁵N and ¹⁴N isotopes while the lighter DNA with ¹⁴N and ¹⁴N, the ratios of two types of DNA was 50:50.
9. In the third generation the ratio of intermediate (¹⁵N and ¹⁴N) was reduced from 50% to 25% while the lighter fraction (¹⁴N and ¹⁴N) increased from (50% – 75%).
10. In the 4^th generation the percentage of intermediate still reduced to 12.5% while that of lighter fraction increased from 75% to 87.5%.
11. These experiments prove that DNA shows semi conservative replication.

Question 30.
What is water pollution? Write short notes on the following with respect to water pollution.
a) Eutrophication
b) Biomagnifications
Answer:
Any undesirable change in the physical, chemical and biological characteristics of water, which makes water unfit for human use and harmfully affect aquatic organisms is called water pollution.

a) Eutrophication
It the process of nutrient enrichment of water bodies and subsequent loss of species diversity like fishes.
Harmful effects

1. Excess nutrients cause algal bloom, which may cover the whole surface of water body and release toxins.
2. It causes oxygen deficiency in water that leads, to the death of aquatic animals like fishes.

b) Biomagnifications
It refers to increase in concentration of toxic substances at successive trophic levels in a food chain. Example: Biomagnifications of DDT in an aquatic food chain.

Harmful Effect
High concentration of DDT disturbs calcium metabolism in birds, which causes thinning of egg shell and their premature breaking, causing decline in bird’s population.

Question 31.
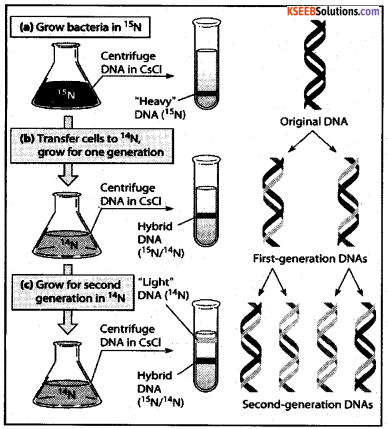
Explain the structure of an anatropous ovule with a neat labeled diagram.
Answer:

Ovule is the female gametophyte develops inside the ovary from a cushion like structure called placenta. It is attached to placenta by a stalk known as funicle. The nutritive tissue enclosed inside the ovule is the nucellus. Nucellus is surrounded by outer and inner integuments. These integu-ments leave a small pore at the anterior end called micropyle. Anterior end of the ovule is micropyle chalazal end is the posterior part.

Question 32.
Distinguish DNA and RNA with respect to their structure or Chemistry and function.
Answer:

DNA	RNA
1. Present mainly in the chromatin the nucleus.	1. Most of RNA is present in the cell of cytoplasm (90%) and a little (10%) in the nucleolus
2. Normally double stranded and rarely single stranded.	2. Normally single stranded and rarely double stranded.
3. It contains deoxyribose sugar.	3. It has ribose sugar.
4. It contains bases like Adenine, Guanine, cytosine and Thymine.	4. It contains bases like, Adenine, Guanine cytosine and uracil.
5. DNA acts as template for its Synthesis.	5. RNA does not act as a template for its synthesis.

Section – II

Answer any THREE of the following questions in 200 – 250 words each, wherever applicable. ( 3 × 5 = 15 )

Question 33.
What is biocontrol? Name the principle behind biological method of pest control. Mention examples of biocontrol agents and their function.
Answer:
It is the use of micro organisms to control or eliminate insect pests. The micro organisms employed in biological control are called bio control agents.

Principle
It is based on prey – predator relationship.

Examples
1. Ladybird and Dragon flies useful to get rid of aphids and mosquitoes.

2. Bacillus thuringiensis (Bt) is used to control butterfly caterpillar. Spores available in sachets are mixed with water and sprayed on plants, eaten by insect larva, toxin released in gut kills larvae.
Example: Bt toxin genes are introduced into cotton plants and made resistant to insect pests such as cotton boll worms, stem borer, aphids and beetles.

3. Nucleo polyhedrovirus ( NPV) is a virus suitable for narrow spectrum insecticide applications. It has no negative impacts on plants, mammals, birds, fish or target insects. It is suitable for overall integrated pest Management programme (IPM) in ecologically sensitive areas.

Question 34.
What is logistic growth? Explain sigmoid curve with a suitable diagram.
Answer:
The rate of population growth slows as the population size approaches carrying capacity, leveling to a constant level.

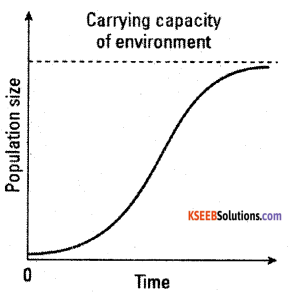
Logistic growth curve or S-shaped growth curve (sigmoid growth curve) is characteristic of all higher animals including man and microbes like yeast cells growing in a natural environment.

Logistic growth is a pattern of growth in which the population density of few individuals introduced into the new habitat increases slowly initially, in a positive acceleration phase (lag phase) then increases rapidly, approaching an exponential growth rate (log phase) due to abundance of food, favourable environmental conditions such a climate, few predators and low levels of disease. Then declines in a negative acceleration phase.

This decline reflects increasing environmental resistance at higher population densities. This type of population growth is termed density-dependent, since growth rate depends on the numbers present in the population. The point of stabilization, or zero growth rates, is termed the saturation value or carrying capacity (K) of the environment for that organism.

When population growth rate is plotted graphically against time S shaped or sigmoid curve is obtained. This type of population growth is also called Verhulst- pearl logistic growth.
The mathematical equation for sigmoid growth is
dN / dt = rN(N – K) / k
Where
N = Population size at a given time
t = Time,
r = intrinsic rate of natural increase
k = Saturation value or carrying capacity for that organism in that environment.

Question 35.
What is animal breeding? Explain the controlled methods of animal breeding and mention their significance.
Answer:
The production of new varieties of animals which are superior to their parents through selective breeding or mating is called animal breeding.
There are two control breeding methods

1. Artificial insemination
2. Multiple ovulation embryo transfer technology (MOET)

Artificial insemination
Semen of superior male is collected and-injected unto the reproductive tract of selected female.

Significance:

1. It helps to overcome several problems of normal mating.
2. Semen of a desirable bull can be inseminated into cows.
3. Semen can be stored by cryopreservation to use at later stages and can be easily transported to distant places.
4. Semen of single ejaculation can be used to inseminate large number of cows.

Multiple Ovulatuion Embryo transfer technology (MOET)
Technique for herd improvement by successful production of hybrids

1. Hormones (FSH) are administered to the cow for inducing follicular maturation and super ovulation.
2. Cow produces 6-8 eggs instead of one egg and is either mated with, superior bull or artificially inseminated.
3. Fertilized egg at 8-32 cell stage are recovered non-surgically & transferred to surrogate mother.

Significance:

1. It is practiced in cattle, sheep, rabbits, buffaloes, etc.
2. Genetically superior animals can be produced.
3. It solves the problems of infertility.
4. A single female can donate many ovules.
5. Preservation and transport of embryos is convenient.

Question 36.
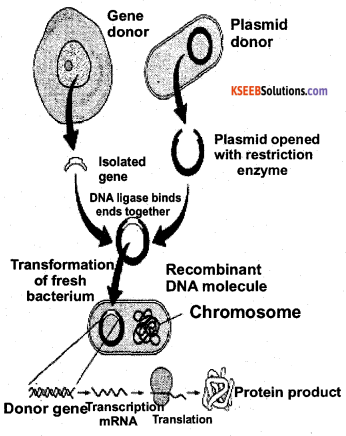
What is recombinant DNA technology? Draw a schematic representation of various steps involved in recombinant DNA technology.
Answer:
The branch of biotechnology that deals with altering the characters of an organism by introducing genes selected from desired organism is called genetic engineering or gene cloning or gene splicing.

Question 37.
What is gametogenesis? Mention the types. Explain spermatogenesis with a schematic representation.
Answer:
The process of formation of haploid male and female gametes in gonads is called gametogenesis.
It is of two types

1. Spermatogenesis
2. Oogenesis

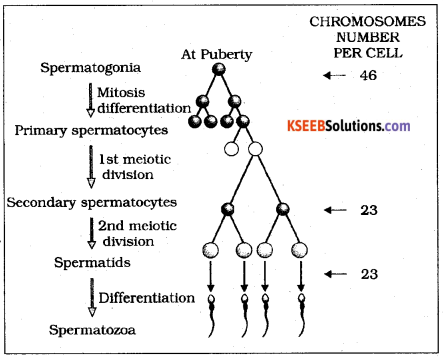
1. Multiplication phase (mitosis)
Each testis is composed of numerous seminiferous tubules. Epithelial cells lining these tubules are called germinal epithelium. At the time of gametogenesis some cells of the epithelium become active, detach from the layer and start dividing mitotically to produce large number of primordial germ cells (2n), in turn primordial germ cells undergo repeated mitotic divisions to form sperm mother cells or spermatogonial cells which are diploid in nature.

2. Growth phase
Some of the spermatogonial cells (2n) stop dividing and enter into the seminiferous tubule where they grow in size by accumulating cytoplasm and duplication of DNA; sertoli or nurse cells provide necessary nutrients for the growing sperm mother cells, now sperm mother cells are termed as primary spermatocytes.

3. Maturation phase (meiosis)
Each primary spermatocyte (2n) enters into first meiotic division and forms two cells with haploid number of chromosomes called secondary spermatocytes. The secondary spermatocytes undergo second meiotic division to give rise to four haploid spermatids. The spermatids are unspecialized cells and do not undergo further division; all the four spermatids are transformed into four haploid sperms. This process of transformation of spermatids into mature and motile sperms is called spermiogenesis or spermateliosis.