Students can Download Basic Maths Exercise 19.4 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 19 Application of Derivatives Ex 19.4
Part-B
Application to Economics
2nd PUC Basic Maths Application of Derivatives Ex 19.4 Two or Three Marks Questions and Answers
Question 1.
Find the Average cost and Marginal cost if the total cost function of an article is given by C = 5x2 + 2x + 3 (x = quantity).
Answers:
Given T.C = C(x) = 5x2 + 2x + 3; M.C = \(\frac{d}{d x}\) (T.C) = 10x + 2
A.C = \(\frac{C(x)}{x}=\frac{T \cdot C}{x}=\frac{5 x^{2}+2 x+3}{x}\) = 5x + 2 + \(\frac{3}{x}\)
Question 2.
The total cost of a commodity is given by C = -x2 + 5x + 7 (x = number of unit) and the price per unit is ₹12. Find the profit function.
Answer:
Given T.C = -x2 + 5x + 7; T.R = 12x
profit function = p(x) = T.R. – T.C = 12x -(-x2 + 5x + 7) = x2 + 7x + 7
Question 3.
For the demand function 2x – 5y = 7 (x = number of unit and y is the price / unit). Find the Total Revenue, Marginal Revenue and Average Revenue.
Answer:
Given 2x – 5y = 7 ⇒ y = \(\frac{2 x-7}{5}\) = price
T.R. = price y quantity = \(\frac{2 x-7}{5} \cdot x=\frac{2 x^{2}-7 x}{5}\)
M.R. = \(\frac{d}{d x}\left(\frac{2 x^{2}-7 x}{5}\right)=\frac{1}{5}(4 x-7)\)
A.R. = \(\frac{T \cdot R}{x}=\frac{2 x-7}{5}\)
![]()
Question 4.
The total cost of L ot output Q is given by C = 300Q – 10Q2 + \(\frac{\mathrm{Q}^{3}}{3}\) Find the output level at which the marginal costand the Average cost attain their respective minimum
Answer:
Given T.C = c(x) = 300Q – 10Q2 + \(\frac{\mathrm{Q}^{3}}{3}\)
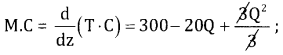
\(\frac{d}{d q}\) (M.C) = 0 ⇒ 2Q – 20 = 0
⇒ Q = 10
\(\frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{q}^{2}}\) (M.C) = 2 > 0 ⇒ MC is Maximum
\(\mathrm{A.C}=\frac{\mathrm{T.C}}{\mathrm{x}}=\frac{300 \mathrm{Q}-10 \mathrm{Q}^{2}+\frac{\mathrm{Q}^{3}}{3}}{\mathrm{Q}}=300-10 \mathrm{Q}+\frac{\mathrm{Q}^{2}}{3}\)
\(\frac{\mathrm{d}}{\mathrm{d} q}(\mathrm{A.C})=-10+\frac{2 \mathrm{Q}}{3}=0 \Rightarrow 2 \mathrm{Q}=30 \Rightarrow \mathrm{Q}=15\)
\(\frac{d^{2}(A C)}{d Q^{2}}=\frac{2}{3}>0\) ⇒ AC is Maximum.
Question 5.
The total cost of the production of a firm in given by the following function C = 0.7x +18 (x = output) Find
(i) the Total cost for an output 10 unit
(ii) the Average cost for an output 9 unit
(iii) the Marginal cost for an output of 6 unit
Answer:
Given C(x) = 0.7x + 18
(a) Total cost when x = 10
C(x) = (0.7 × 10) + 18 = 25
(b) Ave cost when x = 9
\(\mathrm{A.C}=\frac{\mathrm{T.C}}{\mathrm{x}}=\frac{0.7 \mathrm{x}+18}{\mathrm{x}}=\frac{0.7(9)+18}{9}=\frac{24.3}{9}=2.7\)
(C) Marginal cost when x = 6
MC = \(\frac{d}{d x}\) (TC) = \(\frac{d}{d x}\) (0.7x + 18) = 0.7.
Question 6.
If R = 250x + 45x2 – x3, (R = Total Revenue, x = no. of unit) what will be the Marginal Revenue if x = 25 unit and the Average Revenue if x = 10 unit.
Answer:
\(\text { A.R }=\frac{T R}{x}=\frac{250 x+45 x^{2}-x^{3}}{x}=250+45 x-x^{2}\)
When x = 10, A.R = 250 + 450 – 100 = 600
MR = \(\frac{d}{d x}\) (T.R) = \(\frac{d}{d x}\) (250x + 45x2 – x3)
= 250 – 90x – 3x2
At x = 25, M.R = 250 + 25(90) – 75 = 2425
![]()
Question 7.
The total cost function of a manufacturer is C = 5x2 + 500x + 50000. Find the output (x) when AC = MC.
Answer:
Given T.C. = 5x2 + 500x + 50000
A.C. = 5x + 500 + \(\frac{50000}{x}\)
M.C = \(\frac{d}{d x}\) (T.C) = \(\frac{d}{d x}\) (5x2 + 500x + 50,000)
= 10x + 500
![]()
⇒ \(\frac{50000}{x}\) = 5x ⇒ x2 = 10,000
⇒ x = 100
Question 8.
If R = x \(\left(15-\frac{x}{30}\right)\) What is the Marginal Revenue function and what will be the Marginal Revenue if 100 units are produced?
Answer:
Given T.R = 15x – \(\frac{x^{2}}{30}\)
∴ M.R = 15 – \(\frac{2 x}{30}\)
At x = 100 M.R = \(15-\frac{200}{30}=\frac{450-200}{30}=\frac{25}{3}\)
Question 9.
The Total Revenue (R) and the total cost (C) function of a company are given by R(Q) = 300Q – Q2 and C(Q) = 20 + 4Q (Q = output). Find the equilibrium output. (Hint: equilibriums MR = MC).
Answer:
Given T.R = R(Q) = 300Q – Q2
M.R = \(\frac{d}{d q}\) (T.R) = 300 – 2Q
T.C = 20 + 4Q
M.C = \(\frac{d}{d q}\) (T.C) = 4
M.R = M.C ⇒ 300 – 2Q = 4
⇒ 296 = 2Q
⇒ Q = 148.
![]()