Students can Download Basic Maths Exercise 10.1 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 10 Learning Curve Ex 10.1
Part – A
2nd PUC Basic Maths Learning Curve Ex 10.1 One Mark Questions with Answers
Question 1
Define learning curve.
Answer:
Learning curve is defined as curvilinear relation between the decrease in average labour hours’ per unit with the increase in the total output.
Question 2.
Write what does it deals.
Answer:
The theory of learning curve deals with labour efficiency.
Question 3.
Write the learning curve ratio.
Answer:
8th line LCR = Curve ratio
![]()
Question 4.
Write the formula for learning index.
Answer:
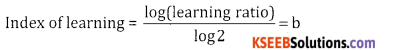
Question 5.
Write the learning curve equation.
Answer:
Y = axb
Question 6.
Find the index of learning for 70% learning effect?
Answer:
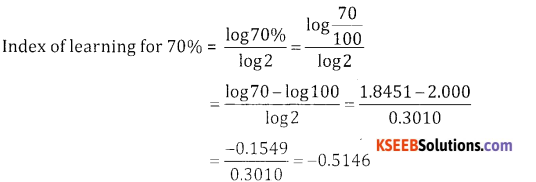
Question 7.
Find the index of learning for 80% learning effect?
Answer:
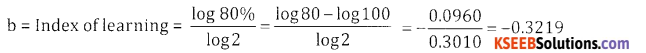
Question 8.
What do you mean by 80% learning effect?
Answer:
80% learning effect means that when the cumulative output is doubled the cumulative average labour hours per unit will be 80% of the previous level.
Question 9.
Calculate the index of learning for 90% L effect.
Answer:
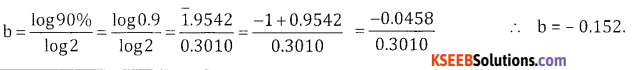
Question 10.
The average labour cost of 1st150 units of production by a factory is ₹ 100, when the output was doubled
to 300 units, the ave labour cost was ₹ 50. Find the L.C.R & the learning curve percent.
Answer:
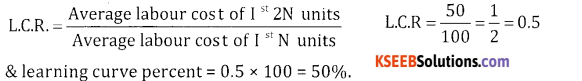
![]()
Part – B
2nd PUC Basic Maths Learning Curve Ex 10.1 Five Marks Questions with Answers
Question 1.
An engineering company has 80% learning effect and spends 1000 hours to produce 1 lot of the product. Estimate the labour cost of producing 8 lots of the product if the labour cost is ₹ 40 per hour.
Answer:
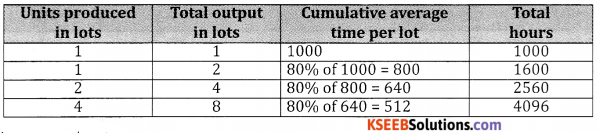
Total time for lots = 4096 hours
Total labour cost at ₹ 40 per hour = 4096 × 40 = ₹ 163840.
Question 2.
ABC company required 1000 hours to produce first 30 engines. If the learning effect is 90% find the total labour cost at 20 per hour to produce total of ₹ 20 engines?
Answer:
Let 30 Engines = 1 unit
∴ 120 engines = units Units
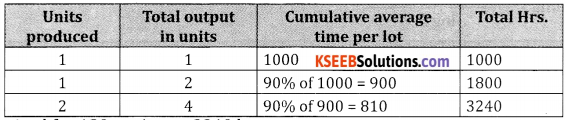
∴ Total time required for 120 engines = 3240 hrs.
Total labour cost at ₹ 20 per hour = 3240 × 20 = ₹ 648000
Question 3.
The production manager of a company obtained the following equation for the learning effect. Y = 1400 X-0.3 This function is based on the company’s experience for assembling the first 50 units of the product. The company was asked to bid a new order of 100 additional units and the labour cost for producing an additional 100 units at the rate of ₹ 20 per hour.
Answer:
Given a = 1400, 1 lot = 50 units = 2 lots = 100 units
∴ x = 2, y = 1400(2) -0.3
Taking logarithm both sides we get
Log Y = log(1400) – 0.3 log(2) = 3.1461 -0.3 × 0.3010
Log y = 3.1461 – 0.0903 = 3.0558
∴ y = A . L (3.0558) = 1137.0 hrs per lot
Total time required for 2 lots = 1137 × 2 = 2274.
Labour cost at for ₹ 20 per hour = 2274 × 20 = ₹ 45480.
![]()
Question 4.
An aircraft manufacturer supplies aircraft engines to different airlines. They have just completed an initial order for 30 engines involving a total of 6000 direct labour hours at ₹ 20 per hour. They have been asked to bid for a prospective contract for a supply of 90 engines. It is expected that there will be 80% learning effect. Estimate the labour cost for the new order.
Answer:
Let 30 engines = 1 unit, 120 engines = 4 units.

∴ Total hours for 90 engines = Total hours for 120 engines – Total hours for 30 engines = 15360 – 6000 = 9360.
The total labour cost for 90 engines at 20 per hour = 9360 × 20 = 1,87,000
Question 5.
A first sample batch of 50 units of product A took 80 hours to make. The company now wishes to estimate | the average time per unit will be if the total output of product A is 200 units and 80% learning rate
applies. Answer: Let 50 units = 1 lot ⇒ 200 units = 4lots

∴ Total hours for 200 units (4 lots) = 204.8 hours and average time per 4 lots
= 51.2 hours
Some Important Questions from Previous Question Papers
Part – C
2nd PUC Basic Maths Learning Curve Ex 10.1 Five Marks Questions with Answers
Question 1.
The time required to produce the first unit of a product is 1000 hours. If the manufacturers experiences 80% learning effect calculate the average time pr unit & the time taken to produce altogether 8 units. Also find the total labour charges for the production of 8 units at the rate of ₹ 12.50 per hour.
Answer:
I. Table method
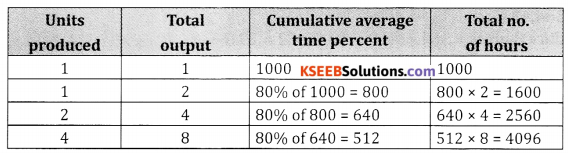
Total time to produce 8 units = 4096 hrs.
Given labour charges for 1 hour = ₹ 12.50
∴Labour charges for 4096 hours = 4096 x 12.50 = ₹ 51,200
II. Formula Method:
Given a = 1000, x = 8 units

y = axb
log y = loga + b log x = log1000 + (-0.3219) log 8
= 3.000 – 0.3219 x 0.9031 = 3.000 – 0.2907
log y = 2.7093
y = AL (2.7093) = 512 hrs. per unit
∴ Total time for 8 units = 512 x 8 = 4,096 hrs.
Labour charges per hour = ₹ 12.50.
∴ Labour charges for 4,096 hrs. = 4,096 x 12.50 = 51,200
Question 2.
An engineering company has won the contract for supplying aircraft engines of a new type. The prototype constructed to win the contract took 500 hours. It is expected that these will have 90% learning effect. Estimate the labour cost of producing 8 engines of new orders. If the labour cost is ₹ 40 per hour.
Answer:
Table Method
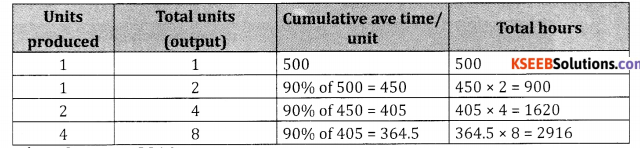
Total time to produce 8 units = 2916
Given labour charges per hour = ₹ 40
:: Labour charges for 2916 hrs. = 2916 ~ 40 = ₹ 1,16,640
Formula Method
Given a = 500 hrs. x = 8,
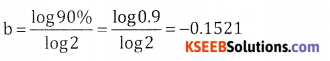
y = axb
log y = log a + b log x
= log 500 – 0.1521 log 8
= 2.6990 – 0.1521 x 0.9031
= 2.6990 – 0.1374
y = AL (2.5616)
= 364.43
∴ Ave time /unit = 364.43
Total time to produce 8 units = 364.43 × 8 = 2915.452 = 2916
Given labour charges 1hr. = ₹ 40
∴Labour charges for 2916 hrs. = 2916 × 40 = 1,16,640.
![]()
Question 3.
The manager of a company obtained the following equation for the learning effect Y= 1450 X-0.2512. The function is based for assembling the first 50 units of the product find the total labour hours required to assemble 100 units.
Answer:
Given the total time for producing a lot of 50 units of a product.
∴ 100 units would constitute 2 lots of 50 units. Each :: 1 = 1450, x = 2, b = -0.2512.
y = axb
log y = log a + b log x
= log 1450 – 0.2512 log2
= 3.1614 – 0.2512 × 0.3010 = 3.0858
y = A.L (3.0858) = 1216 hrs. per lot
∴ Total time required for 2 lots = 2 × 1216 = 2432 hrs.
Question 4.
A manager of a company obtained the following equation for the learning effect y= 200 x-0.3219. The first unit of product requires 200 labour hours. If the company is planning to assemble 100 units of the product find the total labour hours required.
Answer:
Given y = 200 x X-0.3219 Where x = 100 units
Y = 200 × x-0.3219
Where x = 100 units
y = 200 × (100)-0.3219
log y = log 200 – 0.3219 log 100
= 2.3010 – 0.3219 × 2.0
= 2.3010 – 0.6438 = 1.6572
y = A.L (1.6572) = 45.41 per unit
∴ Total labour hours for 100 units = 45.41 × 100 = 4541 hours
Question 5.
The production manager of an electronic company obtained the following equation for the learning effect y = 1356 x -0.3219. The function is based on the company experience for assembling the first 50 units of the product. The company was asked to bid a new order of 100 additional units. Find the labour hours
required to assemble 100 units.
Answer:
Given y = 1356 x-0.3219
Let 50 units = 1 lot
y = 1356(2)-0.3219
∴ 100 units = 2 lots = x
log y = log 1356 -0.3219 log 2
= 3.1322 – 0.3219 (0.3010) = 3.1322 – 0.0969 = 3.0353.
y = A.L (3.0353) = 1085.00 hours /lot
∴ The total no. of labour hours required to assemble 2 lots (100 units) = 1085 2
= 2170 hours.
Question 6.
An aircraft manufacturer supplies aircraft engines to different Airlines. They have just completed an
initial trial order for 30 engines involving a total of 6000 direct labour hours at ₹ 20 per hour. They have been asked to bid prospective contract for supply of 90 engines. It is expected that these will be 80% learning effect. Estimate the labour cost for the new order.
Answer:
Given
a = 6000 hrs., 1 lot = 30 engines, x = 120 engines = 4 lots
Table method
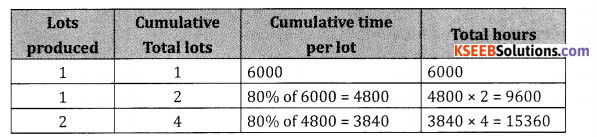
Total time taken to produce 120 engines = 15360
Time taken to produce 30 engines = 6000
Total time taken to produce 90 engines = 15360 – 6000 = 9360
Labour cost at ₹ 20 per hour = 9360 × 20 = 1,87,200
Formula Method
a = 6000 hours, x = 4,
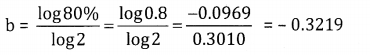
y = axb
log y = log a + b log x
= log 6000 – 0.3219 x log 4
= 3.7782 – 0.3219 × 0.6021 = 3.7782 – 0.1938 = 3.5844
y = A.L (3.5844) = 3841
Total number of hours required to produce 4 lots (120 engines) = 3841 × 4 = 15364 hours.
∴ Total number of hours required to produce 90 engines = 15364 – 6000 = 9364 hrs.
Labour cost at ₹ 20 per hour = 20 × 9364 = ₹ 1,87,280
![]()
Question 7.
A company requires 253.5 hours to produce the 1st 30 units. If the learning effect is 80% Find the number of hours required to produce an additional number of 120 units. Also find the total labour cost at ₹ 20/hr.
Answer:
1 lot = 30 units
120 units = 4 lots

Total time required for 120 units = 648.96 hrs.
Additional time taken for 30 units = 253.5 hrs.
∴ Total time required to complete 150 units = 648.96 +253.5 = 902.46
∴ Total labour cost at 20₹ /hour = 902.46 × 20 = 18049.2
Question 8.
A company requires 2134.2 hours to produce the first 40 machines. If the learning effect is 80%. Find the number of hours required to produce next 120 machines.
Answer:
Let 40 units = 1 lot
120 units = 3 lots

Total time required for 4 lots (160 machines) = 5463.55
∴ Total time for 3 lots (120 machines) = 5463.55 – 2134.20 = 3329.35
Question 9.
The first unit of a product took 80 hours to manufacture. If the workers show 80% learning effect find the
total time taken to produce 6th, 7th & 8th units.
Answer:
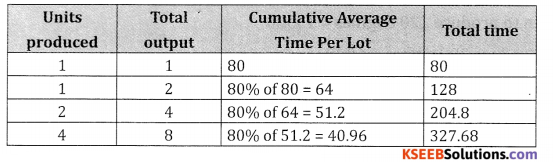
Total time taken to produce 5 units = Time taken to produce
= 4 units + 1 unit = 204.8 + 80 = 284.8
∴ The total time taken to produce 6th, 7th & gth units.
= Time taken to produce 8 units – Time taken to produces 5 units
= 327.68 – 284.8 = 42.88.
Question 10.
A company requires 100 hrs. to produce the fst ten units at 15/per hour. If the learning effect is 80%. Find the total number of hours required to produce 160 units & also the total cost to produce 160 units.
Answer:
Given
a = 100 hrs. 10 units = 1 lot
∴ 160 units = 16 lots
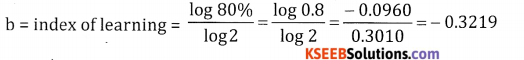
y = axb
log y = log a + b log x
= log 100 – 0.3219 log 16
= 2 – 0.3219 1.2041 = 2 – 0.3875 = 1.625
y = A(1.6125) = 40.98 hours/unit
∴ Total time required for 160 units or 16 lots = 40.98 16 = 655.68 hrs.
∴ Total cost to produce 16 units at ₹ 15/hr. = 655.68 × 15 = ₹ 9835.20
Table method
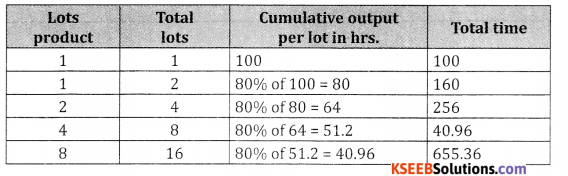
Total time for 16 lots = 655.36 hrs.
∴ Total cost to produce 16 lots at ₹ 15/hr. = 655.36 × 15 = ₹ 19830.4.
![]()
Question 11.
ABC company Ltd., has observed that a 90% learning effect applies to all labour related costs whenever a new product is taken up for production. The anticipated production is 320 units for the coming year. The production is done in lots of 10 units each & each lot requires 1000 labour hours at ₹16 per hour. You are required to compute the total labour hours & labour costs to manufacture 320 units.
Answer:
10 units = 1lot 320 units = 32 lots
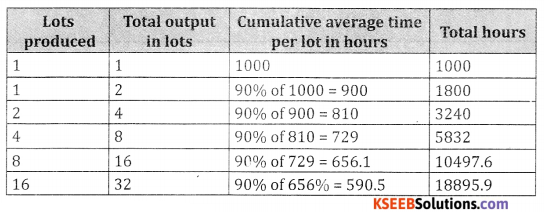
Total labour hours for 32 lots = 18,895.9 hours
Labour cost at 16₹ per hour = 18,895.9 × 16 = ₹ 3,02,334.
Question 12.
A company requires 200 hrs. to produce the first ten units at ₹ 10 per hour. If the learning effect is expected is 90%. Find the total no. of hours required to produce 320 units & also the total cost to produce 320 units.
Answer:
10 units = 1 lot
320 units = 32 lots
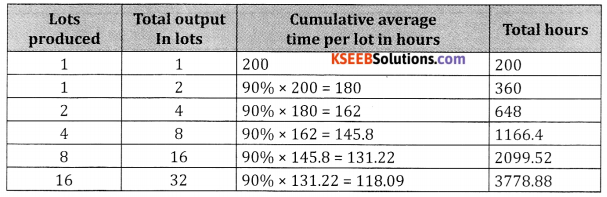
Total number of hours to produce 320 units = 3778.88
∴ Total cost at ₹ 10 per hour = 37762.88 × 10 = 37788.8