You can Download Chapter 6 Analysis of Bivariate Correlation and Regression Questions and Answers, Notes, 1st PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Statistics Question Bank Chapter 6 Analysis of Bivariate Correlation and Regression
1st PUC Analysis of Bivariate Correlation and Regression Two Marks Questions and Answers
Question 1.
What is correlation?
Answer:
Correlation is said to exists between two variables if they vary directly or indirectly together.
Question 2.
Mention different types of correlation.
Answer:
- Positive correlation
- Negative correlation
- zero correlation
Question 3.
Give examples for different types of correlation.
Answer:
- Demand and supply, Height and weight -positive correlation
- Price and demand, price and sales-negative correlation
- Height or Weight of a student and marks obtained in an exam-zero correlation
Question 4.
Define the co-efficient of correlation
Answer:
The degree or the extent of the correlation that exists between the variables is called coefficient of correlation, denoted by gamma (γ).
![]()
Question 5.
What is scatter diagram?
Answer:
When the values of the two variables are plotted on graph on an xy-plane, the spread or the scattered ness of the plotted points gives the types of correlation and the degree of the correlation that exists between the variables, the diagrams is called scattered diagrams.
Question 6.
Define positive correlation and negative correlations.
Answer:
The two variables are said to be positively correlated if they vary in the same direction, eg., demand and supply and, the two variables are said to be negatively correlated if they vary in the opposite direction, eg., price and sales.
Question 7.
What is causation?
Answer:
The cause and effect relationship between the two correlated variables is called causation.
Question 8.
What is spurious correlation?
Answer:
The absence of causation between two variables even though they vary together is called spurious correlation.
Question 9.
Write down any two properties of coefficient of correlation.
Answer:
- It is independent of units of measurement
- It is independent of origin and the scale.
Question 10.
What is the range of correlation co-efficient?
Answer:
γ = ±1 ie., it can take the least value -1 and the highest value +1
Question 11.
What is the value of co-efficient correlation for any two independent variables?
Answer:
γ = 0
Question 12.
Define Rank correlation.
Answer:
The ordinary co-efficient of correlation between the two ranking variables OR the product moment co-efficient correlation between the two ranking variables is called rank correlation, denoted by ‘p’/R
Question 13.
Write any difference between correlation and Rank correlation.
Answer:
Correlation is the measure of relationship between two quantitative characteristics called variables, such as ht. & wt, age & wt, of persons, ages of husbands and wives etc.,Where as the Rank correlation is the measure of relationship of two qualitative characteristics called attributes, such as the aesthetic senses as IQ, Beauty, Intelligence, Taste etc between the persons.
Question 14.
Define the term regression.
Answer:
Regress means go back to the origin, regression means estimation of unknown value of a given variable by knowing all values of the other variable when the variables are correlated
Question 15.
What are regression equations? And write down the two regression equations.
Answer:
The functionai relation developed between the two correlated variables are called regression equations.
The regression equation of x on y is: (X – X̄) = bxy (Y – Ȳ) where bxy-the regression coefficient of x on y.
The regression equation of y on x is: (Y – Ȳ) = bxy (X – X̄) where byx-the regression coefficient of y on x.
![]()
Question 16.
What are regression lines?
Answer:
The graph of regression equations are called regression lines.
17.
What are regressions co-efficient?
Sol.
bxy and byx are called regression co-efficients.
18.
Write the properties of regression lines.
Sol.
- The two regression lines coincides at \((\bar{x}, \bar{y})\)
- The two regression lines intersect when there is a perfect correlation.
- The two regression lines are perpendicular to each other when there is no correlation.
19.
Write the properties of regressions co-efficients.
Sol.
- The regression co-efficients are independent of the origin but dependent on the scale.
- The geometric mean of the two regression co-efficients is numerically equal to the co-efficient of correlation, ie., \(r=\pm \sqrt{b_{x y} \times b_{y x}}\)
- Since the r cannot be greater than 1, so the product of the two regression co-efficients never exceeds 1.
- If the value of one of regression co-efficient is greater than 1 and the other should be less than 1.
1st PUC Analysis of Bivariate Correlation and Regression Problems
Question 1.
Draw a slatter diagram or the following data ant common on correlation.

Answer:
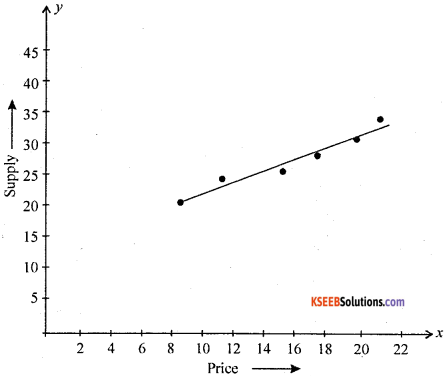
From the diagram, the scatterd points shows raising straight line. There exists a high degree positive correlation between price and supply.
Question 2.
Draw a scatter diagram for the following data and interpret it.

Answer:
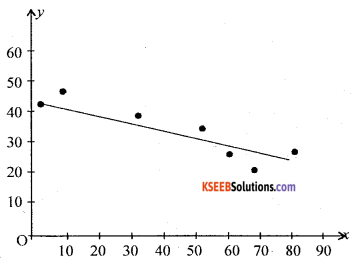
From the scattered diagram, the spraded for the points show down ward diagram. Hence x and y are negatively correlated.
Question 3.
The following data gives the age of a motor cycle and the annual maintenance cost over a period. Find the product moment coefficient of correlation and interpret the same.

Answer:
Let x and y be the age and maintenance cost, the data is small in size, so use direct method.
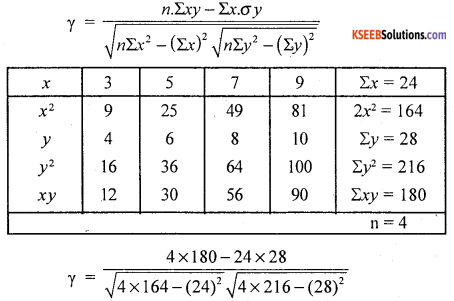
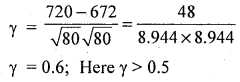
∴ There exists a high degree positive correlation.
Question 4.
Calculate karl pearson’s coefficient of correlation between x and y.

Answer:
The data is large in size, so use step deviation or short cut method.
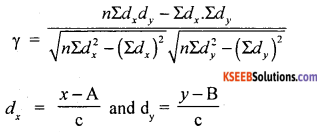
where A, B assumed means and C – common factors from x and y.
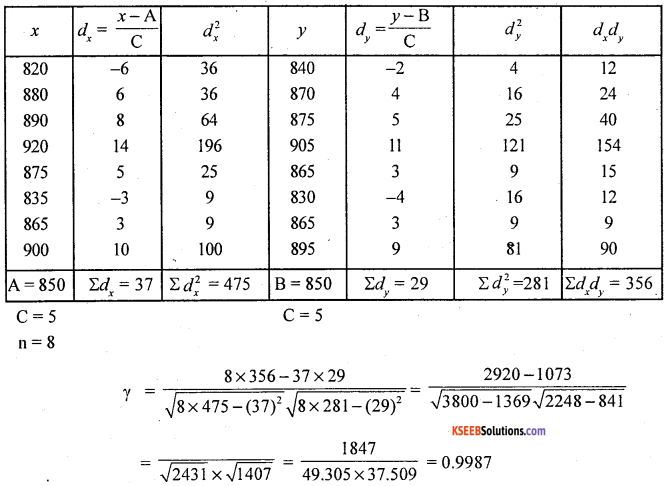
Here γ > 0.5. The exists high degree or close to perfect positive correlation.
![]()
Question 5.
Find K.P.C.C of the following data

Answer:
Let X and Y be ages of husbands and wifes. Here by observation method, Arithmetic means are Whole numbers/ integers. 50, it is convenient to use actual mean method
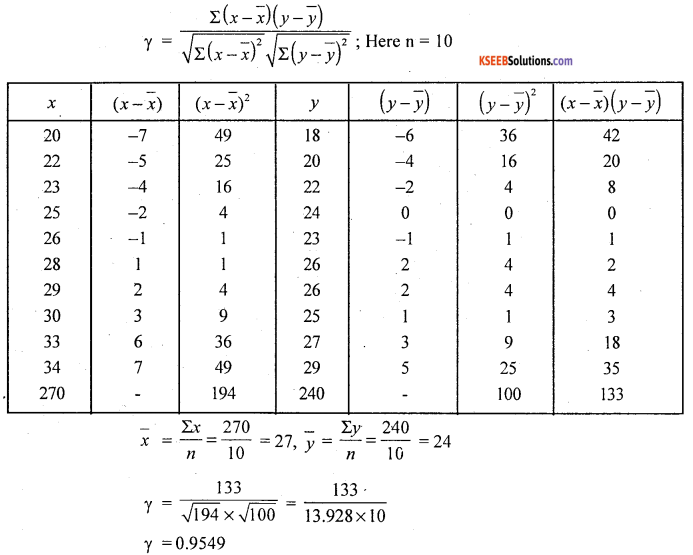
Question 6.
Calculate the coefficient fo correlation between the number of children and age of mothers from the following bivariate frequency table.
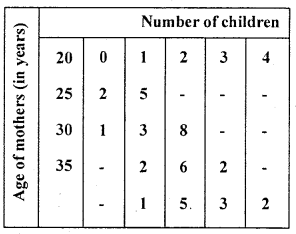
Answer:
Let x and y be the ages of mothers and number of children.
The data is discrete nature for y and with a common difference in x:
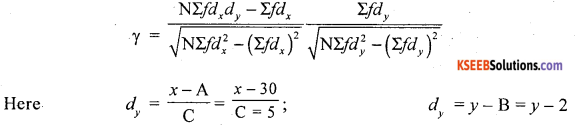
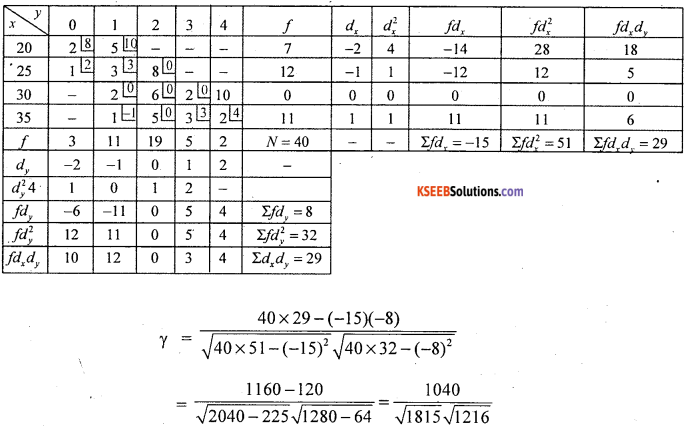
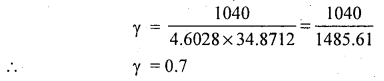
There exists a high degree negative correlation between ages of mothers and number of children.
Question 7.
Calculate the karl pearson’s coefficient of correlation between ages of students and marks obtained in a certain test and interpret.
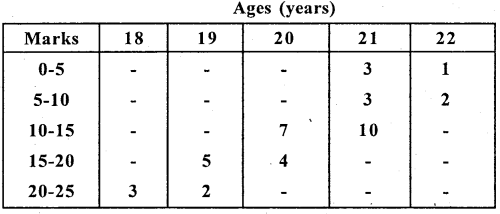
Answer:
Let x and y be the marks and age
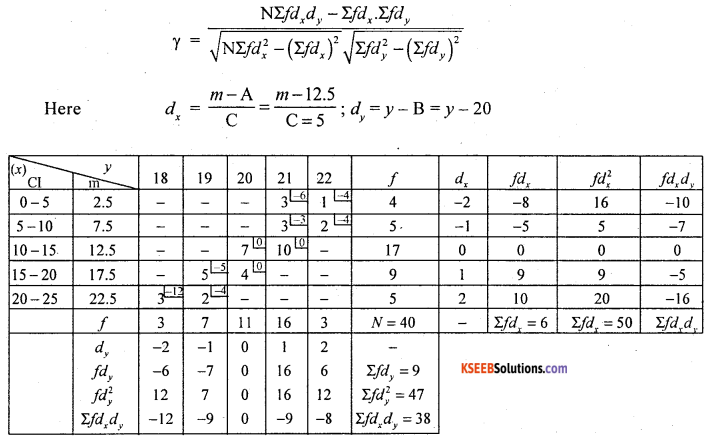
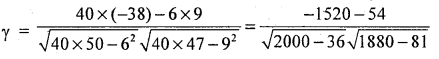
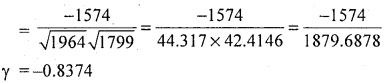
Here, there exists high degree negative correlation between Age of students and their marks.
Question 8.
Calculate K.P.C.C from the following date.
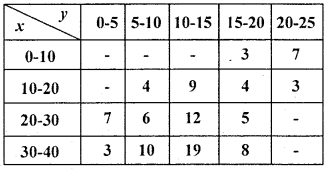
Answer:
Both variables are continuous so, use step deviation method.
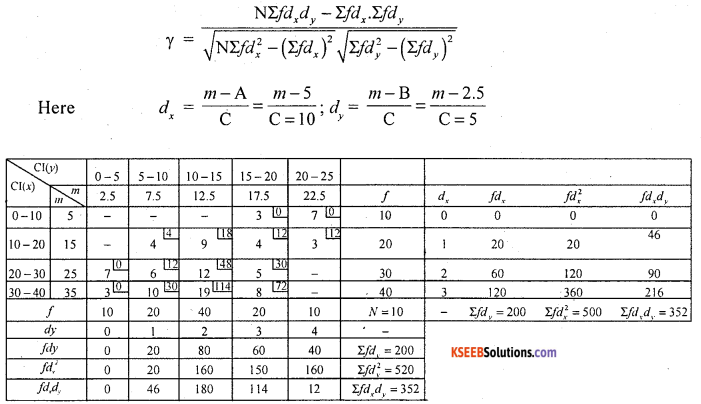
Question 9.
If the covariance between x and y variables is 12.5 and variance of x and y are respectively 16.4 and 13.8. Find the coefficient of correlation between them.
Answer:
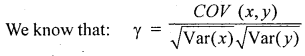
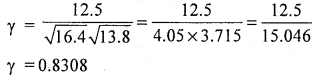
Question 10.
Given COV (x,.y) = -30, Var (x) = 225 and Var (y) = 9, find karl pearson’s coefficient of correlation.
Answer:
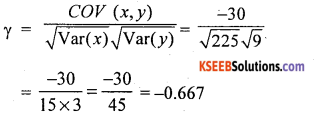
![]()
Question 11.
In a bivariate data, if standard deviations of x and y are 5 and 9 respectively. If the COV (x, y) = 8, find the coefficient of correlation.
Answer:
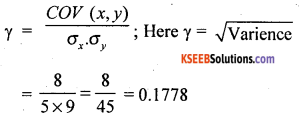
Question 12.
In a bivariate Σ(x – x̄)2 = 35, Σ(x – x̄)2 = 60, Σ(x – x̄)(y – ȳ) = 42. Find the coefficient of correlation
Answer:
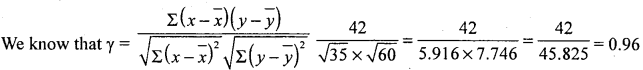
Question 13.
In a bivariate data Σxy = 500, Σx = 15, Σy = 200, Σx2 = 98, Σy2 = 23250 and n = 10. Find the coefficient of correlation.
Answer:

Question 14.
The coefficient of correlation between two variables x and y is 0.65, their covariance is 2.32. The variance of x is 18. Find standard deviation of y.
Answer:
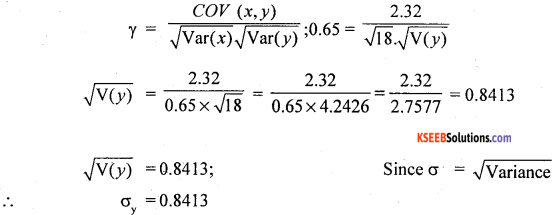
Question 15.
If the coefficient of correlation between x and y is ‘o’ comment.
Answer:
If γ = 0. the two variables x and y are independent, i.e., Non correlated.
Question 16.
Define spurious correlation.
Answer:
Absence of causation between the variables is called sparious correlation.
Question 17.
Calculate spearman’s rank correlation for the following data regarding sports and studies of 8 students:

Answer:
Ranks are given. Let R1 and R2 be the ranks in sports and studies.

There exists low degree negative correlation between sports and studies.
Question 18.
Ten competitors in a pointing competition are ranked by two judges. Using rank correlation find out whether the two judges have common table in painting:

Answer:
Ranks are given. Let R1 and R2 be the ranks of judges I and II

the two Judges have high degree of similar taste in beauty of paintings.
![]()
Question 19.
The corresponding values of 2 series are given below.

Find the coefficient of rank correlation of the above series.
Answer:
Ranks are not given. We have to assign rank. Assign ranks R1 and R2 for the variables x and y in descending order as highest value as 1, 2, upto 7.
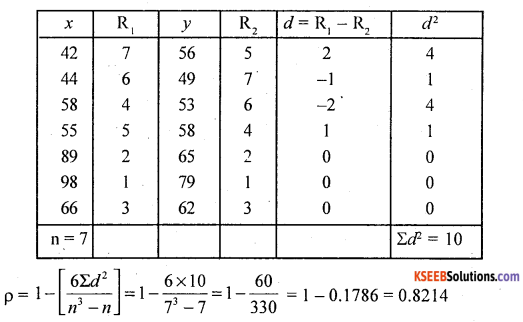
There exsits a high degree positive correlation
Question 20.
Calculate rank correlation from the following marks in Accountancy and statistics

Answer:
Ranks are not given. Assign ranks as R1 and R2 for the marks in Accountancy and statistics as 1st who got highest marks and 2nd to next less marks.
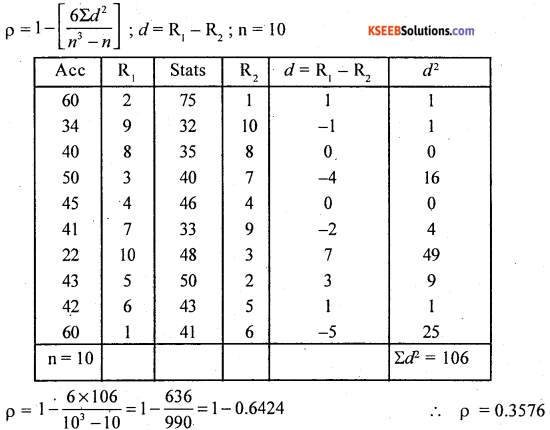
There exists low degree correlation between marks in Accountancy and Statistics.
Question 21.
Calculate rank correlation coefficient from the following data:

Answer:
Here the values of the variables are repeated,
So use, the formula:

m1 = 3 (65 repeated 3 times)
Ranks are averaged as = \(\frac{6+7+8}{3}=7\)
m2 = 2(13 repeated 2 times)
Ranks are averages as = \(\frac{4+5}{2}=4.5\)
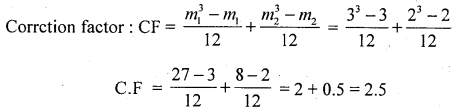
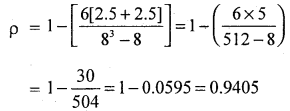
There exists high degree positive correlation between x and y.
Question 22.
Calculate coefficient of correlation undere rank difference method for the following data

Answer:
Repeated values in the variables, so use correation factor formula.

m – available repeated number of times
Let R1 and R2 be the ranks of variables x and y.

There exsits a low degree positive correlation between the variables.
Question 23.
Mention the uses of Rank correlation.
Ans.
Spearman’s rank correlation useful
- To find the correlation between two qualitative characteristics, such as Honesty, Intelligence, Taste etc.
- This method is easy and simple as compared to karl pearsons method when the data has no repetitions.
Question 24.
When do you use Rank method of correlation?
Ans.
Rank method of correlation is used to find correlation between two qualitative characteristics.
Question 25.
The coefficiently rank correlation is 0.75 and the sum of the squares of the difference in rank is 30, then find the value of V.
Answer:
Given: p = 0.75, Σd2 = 30
∴ \(r=1-\frac{6 \Sigma d^{2}}{n^{3}-n}\) \(0.76=1-\frac{6 \times 30}{n^{3}-n}\)
\(\frac{180}{n^{3}-n}=1-0.75=0.25\)
\(\frac { 180 }{ 0.25 }\) = n3 – n 720 = n3 – n
9 × 80 = n(n2 – 1) 9(81 – 1) = n(n2 – 1)
9(92 – 1) = n(n2 – 1) ∴ n= 9
Question 26.
If n = 10 and Σd2 = 200, find the coefficient of rank correlation.
Answer:
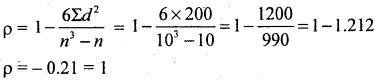
Question 27.
If Σd2 = 182 and r = -0.1030 find ‘n’
Answer:
\(\mathrm{r}=1-\frac{6 \Sigma d^{2}}{n^{3}-n} \quad-0.1030=1-\frac{6 \times 182}{n^{3}-n}\)
\(\frac{1092}{n^{3}-n}=1+0.1030=1.103 ; \quad n^{3}-n=\frac{1092}{1.103}\)
n3 – n = 990 = 10 × 99; n(n2 – 1) = 10(100 – 1)
n(n2 – 1) = 10(102 – 1); ∴ n = 10
![]()
Regression
Question 28.
From the following data:
(a) Calcualte the regression equation of x on y.
(b) Estimate the value of x when y = 40.

Answer:
Regression equation x on y is :
(x – x̄) = bxy (y – ȳ)
Here, x and y variables have their Arithmetic means with whole number / integers. So, it is convenient to use actual mean method.
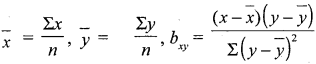

\(n=5 ; \bar{x}=\frac{140}{5}, \bar{y}=\frac{80}{5}=16\)
bxy = \(\frac { 160 }{ 160 }\) = 1
(a) Regression equation of x on y is
x – 28 = 10-16)
x = y- 16 + 28 ∴ x = y + 12
(b) Estimation of x when y = 40
x = 40 + 12 = 52
Question 29.
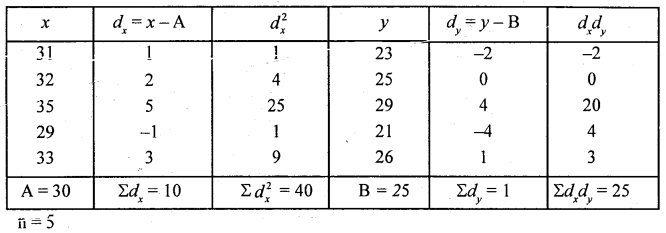
From the following data of the age of Husband (x) and the age of the wife (x) obtain the regression equation of y on x and calculate the wife’s age (y). When husband’s age(x0’s 25 years.

Answer:
Regression equation y on x is (y – ȳ) = byx (x – x̄)
Here x and y variables Arithmetic means are not in whole numbers/ integers. So, it is better to use shortcut method.
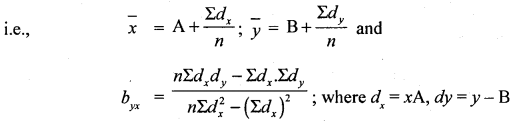
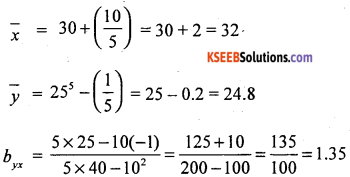
Regression equation of y on x is:
y – 24.8 = 1.35 (x – 32)
y -24.8 = 1.35x – 1.35 × 32
y = 1.35x- 43.2 + 24.8
∴ y = 1.35x – 18.4
Estimation of (y) wife’s age when husbands age (x) is 25:
y = 1.35 (25) – 18.4 = 33.75 – 18.4
y = 15.35 years.
Question 30.
Construct two regression equations for the following data and estimate the value of x when y = 70 and y when x = 650.

Answer:
The two regression equations are:
Regression equation of x on y : (x – x̄) = bxy (y – ȳ)
Regression equation of y on x : (y – ȳ) = bxy (x – x̄)
Both variables having common differences, so use step deviation methods.
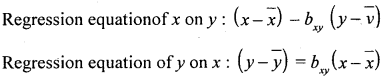
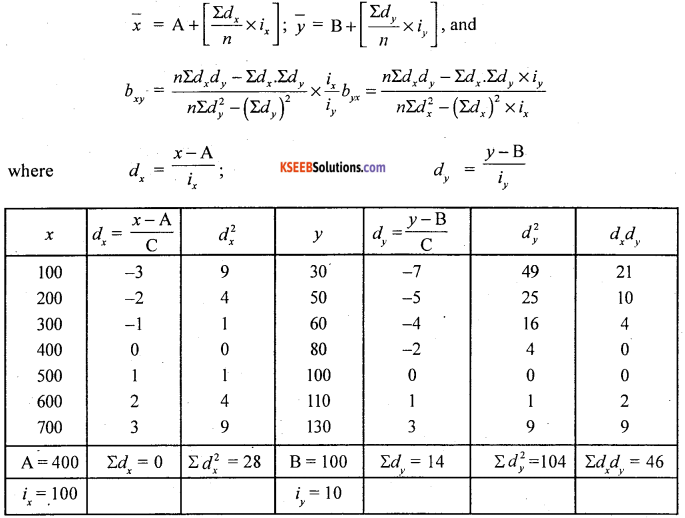
Here ix common width in x = 100
iy common width in v = 10 and n = 7;

Regression equation of x on y:
x – 400 = 6.05 (y-80) = 6.05y-605 × 80
x = 6.05y – 48.4+ 400
Regression equation of x on y : (x – x̄) = bxy (y – ȳ)
x – 14 = 1(y – 8)
x = y – 8 + 14
∴ x = y + 6
and regression equation y on x is : (y – ȳ) = bxy (x – x̄)
y – 8 = 0.8695 (x – 14)
y = 0.8695x – 12.173 + 8
∴ y = 0.8695x -4.173
Estimation of x when y = 20.
∴ From the Regression equation of x on y:
x = 20 + 6 = 26
We know that the coeffiicent of correlation:
\(\gamma=\pm \sqrt{b_{x y} \cdot b_{y x}}=\sqrt{1 \times 0.8695}=0.9325\)
![]()
Question 31.
Eight observations on each of two variables x and y are given below:

1. obtain two regression equation and
2. Find γxy
Answer:
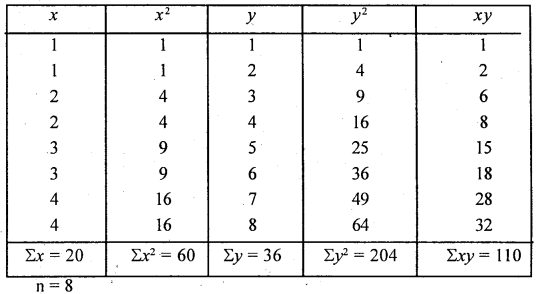
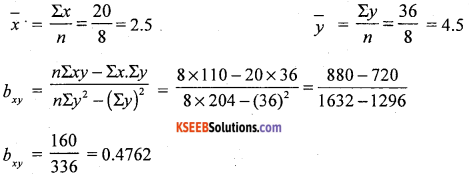
∴ x = 6.05y – 84
pregression equation of y on x:
y – 80 = 0.1643(x – 400)
= 0.1643x – 0.1643 × 400
= 0.1643x – 65.72+80
∴ y = 0.1643x + 14.28
Equation y when x = 70
x = 605 (70) – 84 = 423.5 – 84
∴ x = 339.5
Equation y when x = 650
y = 0.1643(650) + 14.28 = 106.795 + 14.28
y = 121.075
Question 32.
Calculating the regression equation of x on y and y on x from the following data and estimate x when y = 20. Also determine the value of correlation coefficient.

Answer:
The values of x and y varibles are small in size so, use direct method for easy calculation.
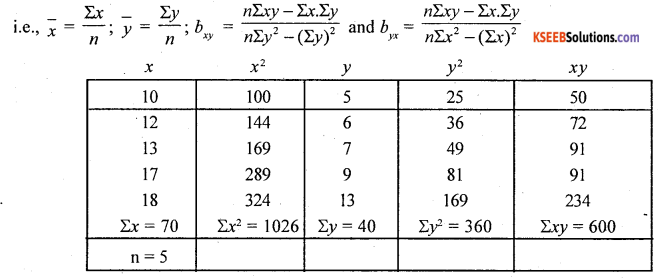

Regression coefficient of x on y: (x – x̄) = bxy (y – ȳ)
x – 2.5 =0.4762 (y – 4.5)
= 0.4762y – 0.4762x
x = 0.4762y – 2.1429 + 2.5
∴ x = 0.4762j + 0.3571
Regression equation of y on x = (y – ȳ) = bxy (x – x̄)
y – 4.5 = 2(x – 2.5)
y = 2x – 2 × 2.5 + 4.5
y = 2x – 5 + 4.5
∴ = 2x – 0.5
We know the relation between coefficient of correlation and the regression coefficients:
\(\gamma=\pm \sqrt{b_{x y} \cdot b_{y x}}=\sqrt{0.4762 \times 2}\)
γ =0.9759
Question 33.
Calculate the two regression equations from the following bivariate table and determine y.
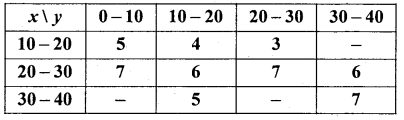
Answer:
For Bivariate, both x andy variables having common differences. So use step deviation method:


Regression equation of x on y : (x – x̄) = bxy (y – ȳ)
x – 25 = 0.256 (y – 19.8)
= 0.256y – 0.256 × 19.8x
=0.256y – 5.0688 + 25
∴ x = 0.256y + 19.9312
Regression equation of y on x = (y – ȳ) = bxy (x – x̄)
y – 19.8 = 0.667(x – 25)
∴ = 0.6667x – 0.667 × 25
y = 0.6667x – 16.675 + 19.8
∴ y = 0.667x + 3.125
and \(\gamma=\pm \sqrt{b_{x y} \cdot b_{y x}}=\sqrt{0.256 \times 0.667}\)
γxy = 0.4132
![]()
Question 34.
Obtain the regression equation of y on x and hence estimate y when x = 32
Answer:
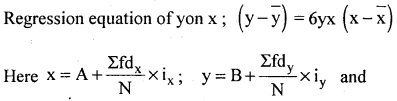
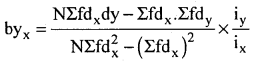
Choose A and B the assumed means as : A = 25, and B = 27.5 from the respective mid points of the variables x and y width x: ix = 10 and width y : iy = 5
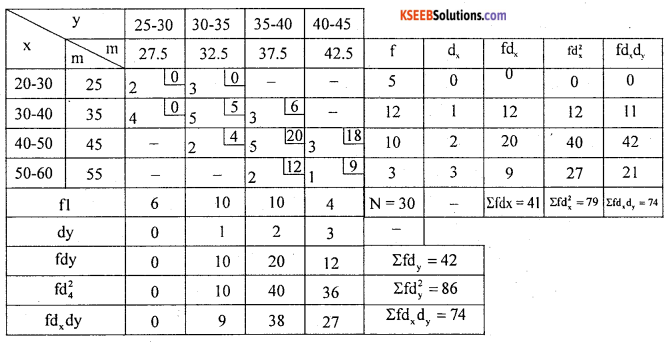
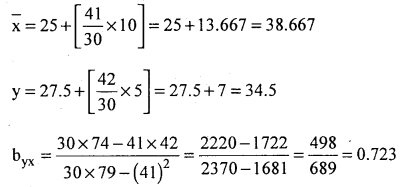
Regression equation of y on x
4 – 34.5 = 0.723 (x – 38.667)
= 0.723 x – 27.96 + 34.5
y = 0.723 x – 27.956+ 34.5
y = 0723x +6.544
Estimation of y when x = 32
y = 0.723 (32)+ 6.544
= 23.136 + 6.544 = 29.68
Question 35.
Find the most probable value of y if x is 70 and the most probable value of x when y 1890 give that
| X series | Y series | |
| Mean | 18 | 100 |
| Standard deviation | 14 | 20 |
co-efficient of correlation between x and y is 0.8
Answer:
Given:
x̄ = 18 ȳ = 100
σx = 14, σy = 20 and γ xy = 0.8
To find y when x = 70 we need regression equation of y on x:

= 1.1429(52)
y = 59.43 + 100
∴ y= 159.43
To find x when y = 90, we need regression equation of x on y.
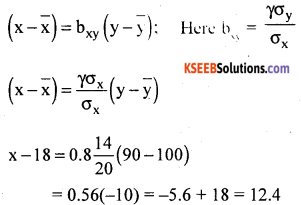
Question 36.
The following data relates to marks obtained by 250 students in accountancy and statistics is 0.8. (i) Esitimate the marks obtained by a student in statistics in II PUC. Examination
| Subject | Arithmetic mean | Variance |
| Accountancy (x) | 48 | 16 |
| Statistics (y) | 55 | 25 |
Co-efficient of correlation between mavasin accountancy and statistics is 0.8
1. Estimate the marks obtained by a student instatistics who secured 50 marks in accountancy and
2. Estimate the marks obtained in accountancy when marks in statistics is 65.
Answer:
Given:
\(\bar{x}=48, \bar{y}=55\) σx2 = 16, ∴ σx = 4
σ24 = 25 ∴ σy = 5 and γ = 0.8
1. Estimation y when x = 50 regression equation of yon x : (y – ȳ) = bxy (x – x̄)
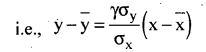
y – 55 = 0.8 \(\frac { 5 }{ 4 }\) (50-48)
y = 1 (2) + 55
∴ y = 2 + 55 = 57
2. Estimation g x when y = 65, use regression equation g x on y : (x – x̄) = bxy (y – ȳ)
![]()
x – 48 = 0.8 ×\(\frac { 4 }{ 5 }\)(65-55)
∴ x = 64+48 = 54.4
![]()
Question 37.
Find two regression equations when x̄ = 68.2, ȳ = 99, \(\frac{\sigma_{y}}{\sigma_{x}}\) = 0.44 and g = 0.76. Also
estimate (a) the most probable value g x when y is 12 (b) the most probable value of 4 when value g x is 16.
Answer:
Given : \(\frac{\sigma_{y}}{\sigma_{x}}\) = 0.44, Also \(\frac{\sigma_{y}}{\sigma_{x}}\) = \(\frac { 1 }{ 0.44 }\) = 2.272
The regression equation of x on y is
![]()
x – 682 = 0.76 × 2.272 (y – 9.9) = 1.7267 y – 1.7267 × 9.9
x= 1.7267 y – 17.0943 + 68.2
∴ x = 17267y + 51.1057
(a) Estimation g x when y = 12
x= 1.7267 (12) + 51.1057 x = 71.8261
The regression equation of yon x is :
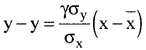
y – 9.9 = 0.76 × 0.44 (x – 68.2) = 0.3344 x – 0.3344 × 68.2 = 0.3344 x – 22.806 + 9.9
y = 0.3344x – 12.906
(b) Estimation of y when x = 16
y = 0.3344 (16) – 2.906 .
y = 5.3504 – 12.906 = – 7.5556
Question 38.
If the regression lines x and y are given by 2x – 3y = 0 and 47 – 5x – 8 = 0. Find the means of JC and y, also the coefficient of correlation.
Answer:
2x – 3y = 0 and 4y – 5x – 8 = 0
Solving both equations we get x and y. And so x̄,ȳ
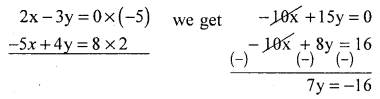
Put y = – 2.286 in 2x – 3y = 0
2x – 3(-2.286) = 0
2x = 6.8568
∴ x = 3.4284
x̄ =3.4284, ȳ = -2.286
Consider, 2x – 3y = 0. be the regression of y on x :
3y = 2x + 0
y = \(\frac { 2 }{ 3 }\)x + 0
∴ byx = \(\frac { 2 }{ 3 }\)
And 4y – 5x = 8 be the regression equation g x on J18
5x = 44 – 8
x = \(\frac { 4 }{ 5 }\)y – \(\frac { 8 }{ 5 }\)x
∴ bxy = \(\frac { 4 }{ 5 }\)
The coefficient of correlation is : \(\gamma=\pm \sqrt{\mathrm{b}_{\mathrm{xy}} \cdot \mathrm{b}_{\mathrm{yx}}}\)
\(\gamma=\sqrt{\frac{4}{5} \times \frac{2}{3}}=0.7303\)
Question 39.
Calculate the two regression coefficients when γ = 0.9, σx = 10, and σy = 1.5
Answer:
Regression coefficient g x ony : \(\mathrm{b}_{\mathrm{xy}}=\frac{\gamma \sigma_{\mathrm{x}}}{\sigma_{\mathrm{y}}}\)
\(b_{x y}=0.9 \times \frac{10}{1.5}=6\)
Regression coefficient of yon x is :\(\mathrm{b}_{\mathrm{yx}}=\frac{\gamma \sigma_{\mathrm{y}}}{\sigma_{\mathrm{x}}}\)
\(b_{y x}=0.9 \times \frac{1.5}{10}=0.135\)
Question 40.
If bxy = 0.8 and byx = 0.6. Find γxy
Answer:
\(\gamma_{x y}=\pm \sqrt{b_{x y} \cdot b_{y x}}=\sqrt{0.8 \times 0.6}=0.6928\)
Question 41.
Find y when the two regression coefficients are 0.6 and – 1.4
Answer:
\(\gamma=\pm \sqrt{\mathrm{b}_{\mathrm{xy}} \cdot \mathrm{b}_{\mathrm{yx}}}=\pm \sqrt{-0.6 \times-1.4}\)
∴ γ = -0.9165 (Based on properties of regression coefficients and correlation coefficient all are negative or positive)
Question 42.
A student calculated the regression co-efficients g xony as – 1.25 abd regression co¬efficient g yon x is -2.40 commenton his calculation.
Answer:
Given bxy =-1.25 and byx =-2.4
It is the property of the two regression coefficient is that, the geometic mean of two regression coefficients is numbericaliy equi to the coefficient of correlation. And coeficient of correlation
taks a value between + 1 and – 1. i.e., \(\gamma=\pm \sqrt{\mathrm{b}_{\mathrm{xy}} \times \mathrm{b}_{\mathrm{yx}}}\)
Here both regression coefficients are more than 1 and so their product is also greater than 1. The students calculation is wrong.
Question 43.
If one of the regression coefficient is 1.5 and y = 0.55, find the value of other regression coefficient.
Answer:
we know that \(\gamma=\pm \sqrt{\mathrm{b}_{\mathrm{xy}} \cdot \mathrm{b}_{\mathrm{yx}}}\)
\(\begin{array}{l}{0.55=\sqrt{\mathrm{b}_{\mathrm{xy}} \times 1.5}} \\ {(0.55)^{2}=\mathrm{b}_{\mathrm{xy}} \times 1.5} \\ {\frac{0.3025}{1.5}=\mathrm{b}_{\mathrm{xy}}}\end{array}\)
∴ bxy =0.2017
![]()