1st PUC Statistics Question Bank Chapter 10 Random Variables and Mathematical Expectation

You can Download Chapter 10 Random Variables and Mathematical Expectation Questions and Answers, Notes, 1st PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.

Karnataka 1st PUC Statistics Question Bank Chapter 10 Random Variables and Mathematical Expectation

1st PUC Random Variables and Mathematical Expectation Two Marks Questions and Answers

Question 1.
Define Random variable.
Answer:
Random variable is a function which assigns a real number to every sample point in the sample space.

Question 2.
Define discrete random variable
Answer:
A random variable ‘ X ’ which takes the specified values x₁x₂,…,x_n with a respective probabilities p₁, p₂,….., p₁ is a discrete random variable.

Question 3.
Define continuous random variable.
Answer:
A random variable which assumes all the possible values in its range is called a continuous random variable.

Question 4.
Define Mathematical expectation of a random variable/Mean of random variable.
Answer:
Let ‘X’ be a discrete random variable which can takes the values x₁, x₂, x₃,… ,x_n with respective probabilities p₁, p₂,p₃,… , p_n then, the mathematical expectation of ‘ X ’ is:E(X) = x₁p₁ + x₂P₂ + x₃P₃ + – + x_nP_n
Then E(X) = Σ x p(x) ;it is also called as mean of discrete random variable (X)

Question 5.
Define probability distribution.
Answer:
A systematic presentation of the values taken by a random variable with respective probabilities is called the probability distribution of a random variable’.

Question 6.
Probability mass function (pmf).
Answer:
Probability mass function (pmf): Let ‘ X ’ be a discrete random variable . And let p(x) be a function : p(x) = p(X=x) . Then p(x) is called the probability mass function of ‘ X ’. If the following conditions are satisfied,

• p(x) ≥ 0 for all values X, and
• Σ p(x) =1.

Question 7.
Probability density function (pdf).
Answer:
Probability density function (pdf): Let ‘ X ’ be a continuous random variable taking values in the interval [a, b], then,
A function f(x) is said to be the probability density function of the continuous random variable ‘ X ’, if it satisfies the following conditions :

• f(x) ≥ 0 for all ‘ X’ in the interval [a, b] .
• For two distinct numbers c & d in the interval [a, b]:
  P(c ≤ X ≤ d) = (Area under the probability curve between ordinates at X =c and X=d).
• Total area under the curve is 1. i.e. , P(- ∞ < x < ∞) = 1 .

Question 8.
Writedown the formulae of all Mathematical Expectations:
Answer:

• E(X) = XΣX.P (X)
• E(a) = a,
• E(aX) = a E(X) and
• E(aX+b) = aE(X)+b.

Question 9.
Write down the Formulae of Variances:
Answer:

• Var(X)= {E(X²)-[E(X)]²} ,
• V (a)=0,
• V(aX)=a² V(X),
• V(aX+b)=a²V(X), and S.D.(X)= \(\sqrt{\mathrm{v}(\mathrm{x})}\).

Question 10.
Write down the Formula of Co-Variance:
Answer:
Cov(X, Y) =E(XY) – E(X).E(Y),

Question 11.
Write down the co-efficient of correlation:
Answer:

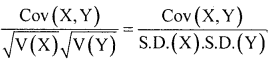
Question 12.
State Addition theorem expectation
Answer:
Statement: Let X and Y be two random variables with respective expectations E(X) and E(Y). Then, E(X + Y)=E(X) + E(Y)

Question 13.
State Multiplication of expectation.
Answer:
statement: Let X and Y be two independent random variables with respective expectations E(X) and E(Y). Then expectation of the product of these random variables is; E(XY) = E(X) E(Y)

Question 14.
If E(X)=2, then find the value of E(-x/4)
Answer:
Given E(-x/4) = E(-l/4. x) =-l/4.E(X) = -1/4. 2 =-1/2 since E(aX) = a E(X)

Question 15.
If E(X)=2/5, find E(5x/3)
Answer:
Given E(5x/3) = E(5/3.x) = 5/3.E(x) = 5/3.2/5 = 2/3

Question 16.
If X is a random variable and E(X) =1.5, then what is the value of E(3 + 4X)?
Answer:
E(3 + 4X) = E(4x + 3) = 4.E(x) + 3 = 4.(1.5) + 3 = 6 +3 = 9 since
E(ax+b) = aE(x)+b

Question 17.
If E(X) = 2, find the value of E(3X – 6).
Answer:
E(3X – 6) = 3E(x) – 6 = 3(2) – 6 =6 – 6 =0

Question 18.
If E(X+Y) =7 and E(X) =4, then find the value of E(Y).
Answer:
We know that E(X+Y) = E(X) + E(Y) ;
7 = 4 + E(y)
E(y) = 7 – 4 = 3

Question 19.
If E(X) = 3 and E(Y) = 5, then find E(3X+2Y), E(3X -Y)
Answer:
E(3X + 2Y) = 3 E(x) + 2 E(y) = 3(3) + 2(5) = 9 + 10=19
E(3X – Y) = 3 E(X) + (-1) E(Y) = 3(3)- 5 = 9 – 5 = 4

Question 20.
If X and Y are two independent random variable, E(XY)=10 and E(X)= 4, then what is the value of E(Y)?
Answer:
We know for any two independent random variables:
E(XY) = E(X)E(Y);
10 = 4 E(Y); E(Y)= 10/4 = 2.5

Question 21.
What is the value of co-efficient of correlation for two independent variables?
Answer:
Zero ie., r = 0

Question 22.
For a random variable X, E(X²) = 50 and V(X)=14, then what is E(X)?
Answer:
We know that V(X) = E(X²)-[E(x)]²
14 = 50-[E(x)]²
[E(x)]² = 50 – 14 = 36
Squaring on both sides, we get E(x) = \(\sqrt{36}\) = 6

Question 23.
If E(X)=3 and E(X²)=45, find the value of S.D.
Answer:
We know S.D(x)
\(\begin{array}{l}{=\sqrt{\mathrm{V}(\mathrm{x})}=\sqrt{\mathrm{E}(\mathrm{X} 2)-[\mathrm{E}(\mathrm{x})] 2}} \\ {=\sqrt{45-[3]^{2}=\sqrt{45-9}}=\sqrt{36}=6}\end{array}\)

Question 24.
If E(X) = 4, E(X²) = 25, find V(5X – 9).
Answer:
V(5x-9)this is of the type V(aX+b)=a²V(X)
V(5x-9) = 5². V(x)
Here V(X) = E(X²) – [E(x)]²;
= 25 – 4² = 25 – 16 = 9
∴ V(5×-9) = 5². V(x) = 25(9) = 225

Question 25.
If V(X)=4 then find V(2X)
Answer:
V(2x) = 2²V(x) = 4 (4) = 16; Since V(aX) = a² V(X)

Question 26.
If V(X) = 5 then find V(-5X).
Answer:
V(-5X) = (5)² V(x) = 25(5) = 125; Since V(aX)=a²V(X)

Question 27.
For a random variable V(X) = 4. Find V(3X +4) and V(-3X).
Answer:
V(3X+4) = 3² V(x) = 9 (4) = 36;
V(-3X) = (-3)² V(x) = 9 (4) = 36; Since V(aX+b)=a² V(X),

Question 28.
If V(x)=1.6, then find V(2X – 5).
Answer:
V(2X-5) = 2² V(x) = 4 (1.6) = 6.4; Since V(aX+b)=a² V(X),

Question 29.
If E(X) = 5, E(Y) = 2, E(XY) = 11, then find Cov(X,Y).
Answer:
We know that Cov(X, Y) = E(XY) – E(X).E(Y)
= 11 – (5) (2)=11 -10= 1.

Question 30.
When X and Y are two discrete random variables with E(X)=5, E(Y)=6, E(X²)=34, E(Y²)=52, and E(XY)=25, then find Cov(X,Y) andin a bi-variate data
Answer:
Cov (X, Y) = E(XY)-E(X).E(Y) = 25 – (5) (6) = 25 – 30 = -5;

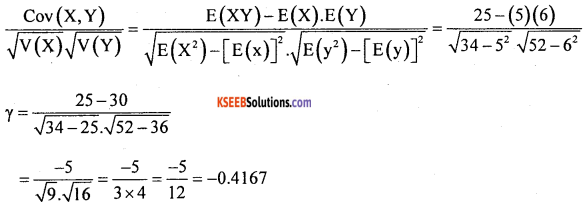
Question 31.
If V(X)=V(Y)=Cov(X,Y), then what is the value of ?
Answer:
γ = 1

Question 32.
If P(X = 3) = 2/3 and P(X = -2) = 1/3, then find E(X) and V(3X + 4)
Answer:
Given probability distribution is:

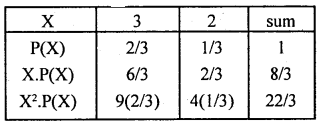
E(x) =8/3;
V(x) = E(X²)-[E(X)]²
= – (8/3)²
= 22/3-7.0756 = 7.3333-7.0756 = 0.2577
V(3X + 4) = 3². V(X) = 9 (0.2577) = 2.3193

Question 33.
If P(X) is a probability mass function (p.m.f) then what is ΣP (x)?
Answer:
ΣP(X)=1

Question 34.
Find the mean and standard deviation for the following probability distribution.

Answer:
We Know that : Mean = E(x) : Σx.P(X)=1
\(=(-2) \times \frac{1}{5}+(-1) \times \frac{2}{5}+0 \times \frac{1}{5}+2 \times \frac{1}{10}+4 \times \frac{1}{10}\)
E(x) =-0.4 -0.4 + 0 +0.2+ 0.4 = -0.2
Var(x) = E(x²) – [E(x)]²
Here E(x²) = [x². P(x)]
\(=(-2)^{2} \times \frac{1}{5}+(-1)^{2} \times \frac{2}{5}+0^{2} \times \frac{1}{5}+2^{2} \times \frac{1}{10}+4^{2} \times \frac{1}{10}\)
= 0.8+ 0.4+ 0 + 0.4+ 1.5
E(x²) = 3.2
∴ Var(x) =3.2-(-0.2)² = 3.2 – 0.04 = 3.16

Question 35.
If two coins are tossed once. Find the mean and variance of number of Heads.
Answer:
S = {HH, HT, TH, TT}
The probability of number of Heads is :

E(x) = Σx. P(x) = \(0 \times \frac{1}{4}+1 \times \frac{2}{4}+2 \times \frac{1}{4}\)
Var (x) = E(X²) [E(x)]²
E(x²) = Ex². P(x) .
\(=0^{2} \times \frac{1}{4}+1^{2} \times \frac{2}{4}+2^{2} \times \frac{1}{4}=0+0.5+1=1.5\)
∴ Var (x) = 1.5 – 1² = 0.5

Question 36.
A fair die thrown once. A person will gets ₹ 5 if the faces of a die results in mulitple of 2. other wise he loses ₹ 2. find his expected amount.
Answer:
Let x denote the expected amount is random variable which can take: 5 (die results in multiple of 2 : 2.46) and -2( die results in 1, 3, 5), with respective probabilities.
P(x = 5) = P(getting multiple of 2) = \(\frac{3}{6}=\frac{1}{2}\)
P(x = -2) = P(Not getting multiple 2) = \(\frac{3}{6}=\frac{1}{2}\)
The probability distribution is :

Expected amount: E(x) = Σx. P(x) = \(5 \times \frac{1}{2}-2 \times \frac{1}{2}=2.5-1\)

Question 37.
A person tosses a fair coin, he gets ₹ 50 if head turns up and loses ₹ 10 if tail appears. Find the expected amount, also find the standard deviation.
Answer:
Let x denote the person to gets the amount is a random variable, which takes the values 50 and -10, with respective probabilities:
P(x = 50) = P(getting Head) = \(\frac { 1 }{ 2 }\) and P(x = -10) = P(getting tail) = \(\frac { 1 }{ 2 }\)
The probability distribution is :

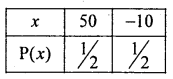
The expected amount: E(x) = Σx. P(x) = 50 × \(\frac { 1 }{ 2 }\) -10 × \(\frac { 1 }{ 2 }\) = 25 – 5 = ₹20

Here E(x²) = Ex². P(x) = (50)² × \(\frac { 1 }{ 2 }\) + (-10)² × \(\frac { 1 }{ 2 }\)
E(x²) = 1250 + 50= 1300
∴ S.D(x) = \(\sqrt{1300-(20)^{2}}=\sqrt{900}\) =₹ 30.

Question 38.
A box has 5 blue and 3 yellow marbles. Two marbles are drawn at random. Find the expected number of blue marbles drawn.
Answer:
Let x denote the number of blue marbles drawn, is a random varible which takes the values: 0, 1,2. The respective probabilities are calcualted as below:
P(x = 0) = P(drawing no blue marbles)
= P(2 yellow marbles) = \(\frac{^{3} \mathrm{C}_{2}}{^{8} \mathrm{C}_{2}}=\frac{3}{28}\)
P(x = 1) = P(drawing one blue and one yellow marbles)
\(=\frac{^{5} \mathrm{C}_{1} \times^{3} \mathrm{C}_{1}}{^{8} \mathrm{C}_{2}}=\frac{15}{28}\)
P(x = 2) = P(drawing two blue marbles) = \(\frac{^{5} \mathrm{C}_{2}}{^{8} \mathrm{C}_{2}}=\frac{10}{28}\)
Then the probability distribution is :

Expected number of blue marbles: E(x) = Σx P(x)
\(=0 \times \frac{3}{28}+1 \times \frac{15}{28}+20 \times \frac{10}{28}=0+0.5357+0.3571\)
∴ E(x) =0.8928

Question 39.
The following is the probability distribution of x. Find k and E(x).

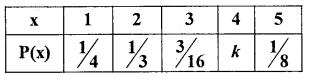
Answer:
For a probability mass funciton : EP(x) = 1
\(\text { i.e., } \frac{1}{4}+\frac{1}{2}+\frac{3}{10}+k+\frac{1}{8}=1\)
\(\mathrm{k}=1-\left[\frac{1}{4}+\frac{1}{2}+\frac{3}{10}+\mathrm{k}+\frac{1}{8}\right]\) ∴K = 1 – 0.8925 = 0.1075
∴ The probability distribution is

E(x) = Σx. P(x) = (1 × 0.25) + (2 × 0.33) + (3 × 0.1875) + (4 × 0.1075) + (5 × 0.125) = 2.5275

Question 40.
From the following probability distribution of x, Find k, E(x), E(x + 3) and Uar (x).

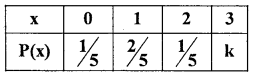
Answer:
By the definition of p.m.f: Σ P(x) = 1
\(\therefore \quad \frac{1}{5}+\frac{2}{5}+\frac{1}{5}+k=1\)  \(\left.\mathrm{k}=-1-\left[\frac{1}{5}+\frac{2}{5}+\frac{1}{5}\right]=0.2+0.4+0.2\right]\)
k = 1 – 0.8 = 0.2
To find E(x), E(2x + 3), (x) and (2x + 3) we need compute from the probability distribution.

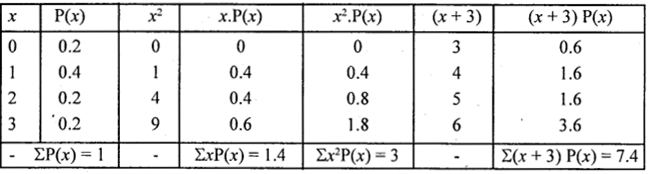
∴ E(x) = Σx. P(x) = 1.4
Var (x) = E(x²) – [E(x)]² = Σx². P(x) – (1.4)²
= 3 – 1.96= 1.04
E(x + 3) = Σ(x + 3) P(x) = 7.4

Question 41.
If x is a discrete random variable and let a, b be two constants, show that
1. E(a) = a
2. E(ax) = aE(x)
3. E(ax + b) = aE(x) + b
4. Var (a) = 0
5. Var (ax) = a² Var (x)
6. Var (ax + b) = a² Var (x).
Answer:
Proof: From the definitions of probability mass function and mathematical expectation
1. E(a) = Σa .P(a) = a. ΣP(x) = a.l = a. ∵ΣP(x) = 1

2. E(ax) = Σax P(x) = aΣx P(x) = a. E(x) ∵Σx P(x) = E(x)

3. E(ax + b) = E(ax + b). P(x) Removing bracket
= Σax. P(x) + Σb.P(x) = aΣx . P(x) + bΣP(x)
= a. E(x) + b. 1 = aE(x) + b

4. Var (a) = E[a – E(a)]²; ∴ V(x) = E[x – E(x)]²
= E[a – a]² = E(0) = 0

5. Var (an) = E[ax – E(ax)]² = E[ax – aE(x)]²; ∴E(ax) = aE(x)
= a²E(x – E(x)]² = a² Var (x)

6. Var (ax + b) = E[(ax + b) – E(ax + b)]²

= E[ax – aE(x)]² = a². E[x – E(x)]² = a² Var (x)

Question 42.
Define joint/ Bivariate probability function.
Answer:
Let x and y be two discrete random variables, then P(x, y) is called bivariate or joint probability function of x and y, if P[x = x] and P(y = y)

Question 43.
Define margined probability functionof x.
Ans.
Margined probability function of x: P(x) is obtained from the joint probability faction of P(x,y).

Question 44.
Define marginal probability function of y.
Ans.
Marginal probability function of y: P,(y) 1’s obtained from the joint probability function of P(x, y).

Question 45.
State and prove the addition theorem of mathematical expectation. ’
Answer:
Statement: Let x and y be random variables with respective expectations E(x) and E(y). Then, the expectations of the sum of the random variables is
E(x + y) =E(x) + E(y)
Proof: Let x and y be two discrete random variables, with their joint probability function : P(x, y) as,
P(x,y) =P(x = x, y = y)
The marginal probability distributions of x and y are:

Question 46.
State tne prove multiplication theorem of mathematical expectation.
Answer:
Statement: Let x and y be two independent discrete random variables with respective expectations E(x) and E(y). then the expectation of the product of these random variables is: E(xy) = E(x) . E(y)
Proof: Let x and y be two independent discrete random variables, then joint probability function P(x, y) is
P(x, y) = P₁(x). P₂(y) ……(i)
Then, by the defintion of mathematical expectation.

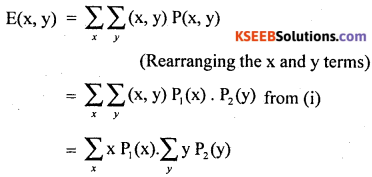
From the definition mathematical expectation
E(x y) = E(x) . E(y), Hence the proof.

Question 47.
Find, Mean, Variance of the following probability distribution.

Answer:
Mean = E(x) = Σx . P(x)
= (-2) × 0.05 + (-1) 0.2 + 0 × 0.25 + 1 × 0.4 + 2 × 0.1
= -0.1 – 0.2 + 0 + 0.4 + 0.2 = 0.3
Var(x) =E(x²) – [E(x)]²
E(x²) = Σx². P(x) = (-2)² x 0.05 + (-1)² x 0.2 + 0 x 0.25 + 1 x 0.4 + 2 x 0.1
= 0.2 + 0.2 + 0 + 0.4 + 0.2 = 1
∴ Var (x) = 1 – (0.3)² = – 0.09 = 0.91

Question 48.
For the following probability distribution find E(x), E(2x + 5), E(x2 + 3), V(x), V(2x).

Answer:
E(x) = Σx . P(x)
= 1 × 0.3 + 2 × 0.4 + 3 × 0.3
= 0.3 + 0.08 + 0.9 = 20
and E(x²) = Σx². P(x)
= 1² × 0.3 + 2² × 0.4 + 3² × 0.3
= 0.3 +1.6+ 2.7 = 4.6
Var (x) = E(x²) – [E(x)]² = 4.6 – (2)² = 0.6
E(2x + 5); From the results : E(ax + b) = aE(x) + b
= 2E(x) + 5; Since E(x) = 2
E(2x + 5)=2 × 2 + 5 = 9
E(x² + 3) = E(x²) + 3 = 4.6 + 3 = 7.6
∴ Var (2x) = 2² Var (x) = 4 x 0.6 = 2.4

Question 49.
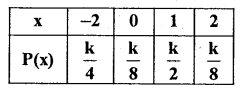
From the Following probability distribution. find k, E(x), E\(\left(\frac{x}{3}\right)\), E(-4x) Var (x) Var (5x) var \(\left(\frac{2 x}{3}\right)^{3}\), Var (-3x).

Answer:
We know from the probability mass function. ΣP(x) = 1
\(\therefore \quad \frac{\mathrm{k}}{4}+\frac{\mathrm{k}}{8}+\frac{\mathrm{k}}{2}+\frac{\mathrm{k}}{8}=1\) \(k\left[\frac{1}{4}+\frac{1}{8}+\frac{1}{2}+\frac{1}{8}\right]=1\)
K.1 = 1; ∴K = 1
The probability distribution reduce now,

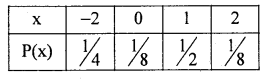
\(\mathrm{E}(\mathrm{x})=\Sigma \mathrm{x} . \mathrm{P}(\mathrm{x})=(-2) \times \frac{1}{4}+0 \times \frac{1}{8}+1 \times \frac{1}{2}+2 \times \frac{1}{8}\)
= -0.5 + 0+ 0.5 + 0.25
E(x) = 0.25
\(\mathrm{E}\left(\mathrm{x}^{2}\right)=(-2)^{2} \times \frac{1}{4}+0^{2} \times \frac{1}{8}+1^{2} \times \frac{1}{2}+2^{2} \times \frac{1}{8}\)
= 1 + 0 + 0.5 + 0.5 = 2
Var (x) = E(x²) – [E(x)]²
= 2 – (0.25)² = 2 – 0.0625 = 1.9375
\(\mathrm{E}\left(\frac{\mathrm{x}}{3}\right)=\mathrm{E}\left(\frac{1}{3} \cdot \mathrm{x}\right)\); From E(ax) = aE(x)
\(=\frac{1}{3} \mathrm{E}(\mathrm{x})=\frac{1}{3} \times 0.25=0.083\)
E(-4x) = -4E()x = -4 × 0.25 = -1
Var (5x) = 5² var (x); from Var (ax) = a² Var (x)
= 25 × 1.9375 = 48.4375
Var\(\left(\frac{2 x}{3}\right)\) = Var\(\left(\frac{2}{3} \cdot x\right)\)
= \(\left(\frac{2}{3}\right)^{2}\)Var(x) = \(\frac { 4 }{ 9 }\) x 1.9375 = 0.861
Var (-3x) = (-3)² Var (x) = 9 × 1.9375 = 17.4375

Question 50.
A purse has 5 Ten rupee coins, 3 five rupee coins and 2 two rupee coins. A coin is drawn at random from the purse. Find expectation of amount draw.
Answer:
Let x denote the expected amount drawn, is a discrete random variable which takes the values : x = 10, 5, 2 with the prababilities
P(x = 10) = P(drawing ₹ 10 coin) = \(\frac { 5 }{ 10 }\)
P(x=5)= \(\frac { 3 }{ 10 }\). P(x = 2)=\(\frac { 2 }{ 10 }\)
Then, the probability distribution is

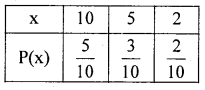
Expected amount draw : E(x) = Ex. P(x)
\(=10 \times \frac{5}{10}+5 \times \frac{3}{10}+2 \times \frac{2}{10}=\frac{50}{10}+\frac{15}{10}+\frac{4}{10}\) = ₹ 6.90

Question 51.
In a lottery there are 1000 tickets costing ₹5 each. There is one first prize worth ₹ 1000. Two second prizes worth ₹ 500 each and ten third prizes worth ₹ 100 each. Find expected gain in buying one lottery ticket.
Answer:
Let x denote the expected gain is a discrete random variable which takes the values x : 995, 495, 95 and -5. Since he buys a ticket of for ₹ 5 is deducted). The respective probability can be calculated as below:
p(x = 995) = \(\frac { 1 }{ 1000 }\): p(x = 495) = \(\frac { 2 }{ 1000 }\)
p(x = 95) = \(\frac { 10 }{ 1000 }\) p(x = -5) = \(\frac { 987 }{ 1000 }\)
The probability distribution is :

Expected gain : E(x) = Σx. P(x)
\(=995 \times \frac{1}{1000}+495 \times \frac{2}{1000}+95 \times \frac{10}{1000}-5 \times \frac{987}{1000}\)
= 0.995 + 0.99 + 0.95 – 4.985 = -2.47
i.e., expected loss in buying a lottery ticket is ₹ 247.

Question 52.
A person enters into a fair by paying ₹10. In the fair if choose to hit a target with airgun by paying ₹ 1 per shot if he hits gets ₹ 50. The probability of hitting a target is 1/2. Find the expect amount.
Answer:
Let x denote the expect amount is a discrete random variable, which takes the values : -11, 39.
The respective probabilities
P(x = -11) = P(not hitting a target) = \(\frac { 2 }{ 3 }\)
P(x = 39) = P(hitting a target) = \(\frac { 1 }{ 3 }\)
Therefore, the expected amount is :
E(x) = Σx. P(x)
= -11 × \(\frac { 2 }{ 3 }\) + 39 × \(\frac { 1 }{ 3 }\) = -7.33 + 13 = Rs. 5.67 profit.

Question 53.
Find expected sum of numbers obtained in a throw of two dice.
Answer:
Let x and y be the numbers appeared on the faces of two dice is a discrete random variable, then each die show with numbers 1, 2,3, 4, 5, 6 with respective probabilities \(\frac { 1 }{ 6 }\) each.
Expected number obtained on the first die be : E( x) = Σx . P(x)
\(=1 \times \frac{1}{6}+2 \times \frac{1}{6}+3 \times \frac{1}{6}+\ldots \ldots+6 \times \frac{1}{6}=3.5\)
Similarly, expected number on the faces of 2^nd die be E(y) = 3.5
The expectation of sum of numbers obtained is
E(x + y) = E(x) + E(y) = 3.5 + 3.5 = 7
Note: Similarly, sum of’ ‘n’ dice of numbers can be calcualted.

Question 54.
A bag has ten tiny of dice. Two dice are randomly drawn. Find the expectation of the product of the numbers obtained on the faces of dice.
Answer:
Let x and y denoted the numbers obtained on the faces of dice, is a discrete random variable with values 1, 2,…. 6 and with the probability \(\frac { 1 }{ 6 }\) each.
Therefore E(x) = \(1 \times \frac{1}{6}+2 \times \frac{1}{6}+\ldots \ldots+6 \times \frac{1}{6}=3.5\)
Similarly, E(y) =3.5
Since, drawing dice are independens, therefore
E(x, y) = E(x) . E(y) = 3.5 × 3.5 = 12.25
Note: Similarly product of’n’ dice of numbers can also be calculated in the square way.

Question 55.
If in a bivoriate data, E(x) = 4, E(x²) = 25, E(y) = 8 and E(y²) = 100 and E(x y ) = 24. Find Var (x), Var (y), Cov (x, y) and the coefficient of correlation (3xy).
Answer:
Var (x) = E(x²) – [E(x)]² = 25 – 4² = 9
Var (x) = E(y²) – [E(y)]² = 100 – 8² = 36
COV (x, y) = E(xy) – E(x) . E(y) = 24 – 4 x 8 = -8

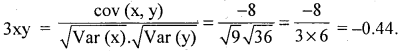
Question 56.
In a bivariate data E(x) = 1.3. E(x²) = 3.4, E(y) = 0 and E(y²) = 4. E(xy) = 0.1 Find S.D(x), SD(y) and rxy.
Answer:

Question 57.
For the following bivariate probaiblity distribution, find E(x + y) and E(xy).

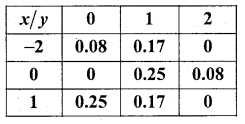
Answer:

Here 0.08, 0.17, 0.25, 0.08, 0.25 and 0.17 are joint probability function P(x, y) of discrete random variables x and y.
E(x.y) =(-2) × 0 × 0.08 + 0 × 0 × 0+1 × 0 × 0.25 + (-2) × 1 × 0.17 + 0 × 1 × 0.25 + 1 × 1 × 0.17 +(2) × 2 × 0 + 0 × 2 × 0.08+ 1 × 2 × 0.
= (0 + 0 + 0) +(0.34 + 0 + 0.17) + (0 + 0 + 0)
∴ E(x.y) =0.17

= (-2 + 0) 0.08 + (0 + 0) 0 + (1 + 0) 0.25 + (-2 + 1) 0.17 + (0 + 1)0.25 + (1 + 1)0.17+ (-2 +2) +0 + (0 + 2) 0.08+ (1 +2)0 = (-0.16 + 0 + 0.25) + (-0.17 + 0.25 + 0.34) + (0 + 0.16 + 0)
= 0.09 + 0.42 + 0.16.
E(x + y) =0.67

Question 58.
From the following bivariate probability distribution, find the coefficient of correlation.

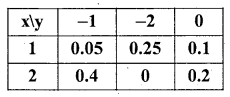
Answer:
The coefficient of correlation is :

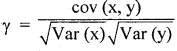
Here Var(x) = E(x²) – [E(x)]²
‘To calculate, obtain the marginal probility distribution of x:

Here : 0.05 + 0.25 + 0.1 = 0.4 and 2 : 0.4 + 0 + 0.2 = 0.6
E(x) = Ex . P(x) = 1 × 0.4 + 2 × 0.6 = 1.6
E(x²) = Ex². P(x) = 1² × 0.4 + 2² × 0.06 = 2.8
∴ Var (x)= 2.8 — (1.6)² = 0.24

The marginal probability distribution of y:

E(y) = Ey P(y) = (-1) × 0.45 + (-2) × 0.25 + 0 × 0.3 = – 0.95
E(y2) = (-1 )² × 0.45 + (-2)² × 0.25 + 0² × 0.3 = 0.45 + 1 + 0 = 1.45
∴ Var(y) = E(y²) – [E(y)]² = 1.45 – (-0.95)² = 1.45 – 0.9025 = 0.5475
cov (x, y) = E(xy) – E(x) . E(y)

= (1 × (-1) × 0.05) + (2 × (-1) × 0.4) + (1 × (-2) × 0.25) + (2 × (-2) × 0) + (1 × 0 × 0.1) +(2 × 0 + 0.2)
= -0.05 -0.8 -0.5 + 0 + 0 + 0
E(xy) =-1.35
∴ cov(x,y) =-1.35- 1.6 x (-0.95) = -1.35 + 1.52 = -0.17

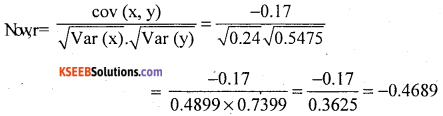
Question 59.
If E(x²) = 65, and E(x) = 4. Find standard deviation of x.
Answer:
Here,

Var(x) = E(x²) = [E(x)]² = 65 – (4²) = 65 – 16 = 49

Question 60.
IfVar(x)=0.4327, and E(x2) = 0.75. Find E(x).
Answer:
Var(x) = E(x²) – [E(x)]²
0.4327 = 0.75 – [E(x)]²
[E(x)]² =0.75-0.4327 = 0.3153
∴ E(x) = \(\sqrt{0.3153}\) =0.5615

Question 61.
If x and y be two independent random variable with E(xy) = 8, and E(x) = 2, then find E(y).
Answer:
Since x and y are independent then E(xy) = E(x). E(y)
i.e., 8 = 2. E(y) ∴ E(y) = 2

Question 62.
For a bivariate data if E(x) = 5, E(y) = 3, E(x²) = 45, E(y²) = 85 and E(x) = 18. Find yxy.
Answer:

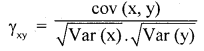
so, Var (x) = E(x²) = [E(x)]² = 45 – (5)² = 45 – 25 = 20
Var (y) = E(y²) – [(y)]² = 85 – (3)² = 85 – 9 = 76
COV (x, y) = E(xy) – E(x) . E(y) =18-5 x 3 = 18- 15 = 3
∴ \(\gamma=\frac{3}{\sqrt{20} \times \sqrt{76}}=\frac{3}{4.472 \times 8.718}=\frac{3}{38.987}=0.0769\)

Question 63.
If E(x) = 5 and E(y) = 12, find E(x + y), E(x – y), E(4x + 2y), and E(-3x + 2y).
Answer:
E(x + y) = E(x) + E(y) , by theorem = 5 + 12= 17
E(x-y) = E(x) – E(y) = 5 – 12 = -7
E(4x + 2y) = 4E(x) + 2E(y) = 4 × 5 + 2 × 12 = 20 + 24 = 44
E(-3x + 2y) = (-3) E(x) + 2E(y) = (-3) × 5 + 2 × 12 = 15 + 24 = 9

Question 64.
If Var (x) = 3, find Var (5x), Var (-8x), Var (-x), Var (4x – 5) and Var (8 – 3x)
Answer:
V(5x); By the results ; Var (ax) = a² Var (x)
∴ Var (5x) = 5² Var (x) = 25 x 3 = 75
Var (-8x) = (-8)² Var (x) = 64 x 3 = 192
Var (-x) = Var (-1 .x) = (-1)2 Var (x) = 1 x 3 = 3.
Var (4x – 5); using the result; Var (ax + b) = a² Var (x)
∴ Var(4x – 5) = 4² Var (x) = 16 x 3 = 48
Var (8 – 3x) = Var (-3x + 8) = (-3)² Var (x) = 9 x 3= 27