Students can Download Maths Chapter 11 Conic Sections Questions and Answers, Notes Pdf, 1st PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Maths Question Bank Chapter 11 Conic Sections
Question 1.
Name the different conics.
Answer:
Circle, parabola, ellipse and hyperbola.
Circles
Question 2.
Define a circle and derive the equation of the circle whose centre and radius is given.
Answer:
Definition: A circle is a set of all points in a plane that are equidistant from a fixed point in a plane. OR A circle is the locus of a point which moves in a plane such that its distance from a fixed point in the plane is constant.
Note:
- Fixed point is called centre.
- The distance from the centre to a point on the circle is called radius.
Equation of a circle, given its centre and radius:
Let C(h,k) be the centre y and r, the radius of the circle. Let P(x,y) be any point on the circle. Then, by definition, |CPl = r
∴ By distance formula, we have
\(\sqrt{(x-h)^{2}+(y-k)^{2}}=r\)
\(\text { i.e., }(x-h)^{2}+(y-k)^{2}=r^{2}\)
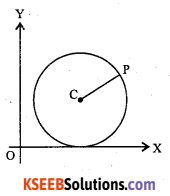
Note: If the centre is at the origin ,then h = 0,k = 0. Therefore the equation of the circle with centre at the origin and radius r is x2 + y2 = r2
Question 3.
Find the equation of the circle with
(i) Centre (0,0) and radius r
(ii) Centre (0,2) and radius 2
(iii) Centre (-2,3) and radius 4
(iv) Centre (-3,2) and radius 4.
(v) Centre (1,1) and radius \(\sqrt{2}\)
(vi) \(\text { Centre }\left(\frac{1}{2}, \frac{1}{4}\right)\) and radius \(\frac{1}{12}\)
(viii) Centre (-a,-b) and radius \(\sqrt{a^{2}-b^{2}}\)
Answer:

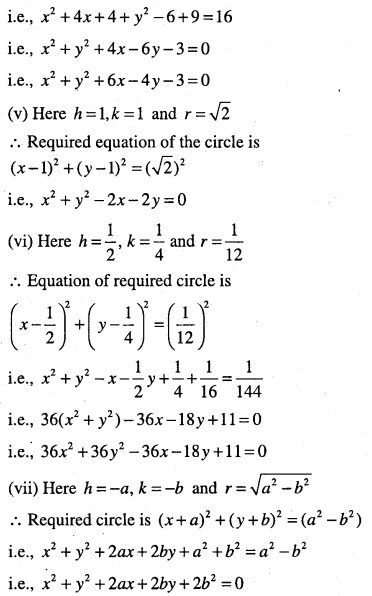
![]()
Question 4.
Write the standard form (General form) of a circle.
Answer:
Standard form of a circle is x2 + y2 + 2 gx + 2 fy + c = 0
(∵ in the above problems, we observe that the equations of the circles are of the form
x2 + y2 + ( )x + ( )y + () = 0
Note:
- Centre = (-g, -f)
\(\text { Radius }=\sqrt{g^{2}+f^{2}-c}\) - The co-efficients of x2 and y2 are equal to unity.
- There is no term containing the product xy.
- If g2 + f2 -c > 0, then the circle is real circle.
- If g2 + f2 – c = 0, then the circle is a point circle.
- If g2 + f2 – c< 0, then the circle is imaginary circle.
- If the centre of the circle is on the x-axis, then equation of the circle is
x2 + y2 + 2gx + c = 0 and conversely. (Here f = 0) - If the centre of the circle is on the y-axis, then the equation of circle is
x2 + y2 + 2fy + c = 0 and conversely. (Here g = 0) - In the equation, x2 + y2 + 2gx + 2fy + c = 0, if c = 0, then the circle passes through the origin and circle equation is x2 + y2 + 2gx + 2fy = 0
Question 5.
Find the centre and radius of the circles.
(i) x2 + y2 + 2gx + 2fy + c = 0
(ii) x2 + y2 + 8x + 10y -8 = 0
(iii) x2 + y2 – 4x – 8y – 45 = 0
(iv) x2 + y2 – 8x – 10y -12 = 0
(v) (x + 5)2 + (y – 3)2 = 36
(vi) 2x2 + 2y2-x = 0
Answer:




![]()
Question 6.
Find the equation of the circle passing through the points (2, -2) and (3, 4) and whose centre lies on the line x + y = 2
Answer:

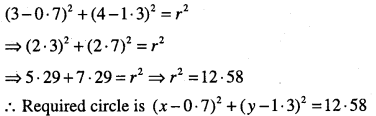
Question 7.
Find the equation of the circle
(i) passing through the points (4, 1) and (6, 5) and whose centre lies on 4x + y = 16.
(ii) Passing through the points (2, 3) and (-1, 1) and centre is on the line x – 3y -11 = 0.
Answer:

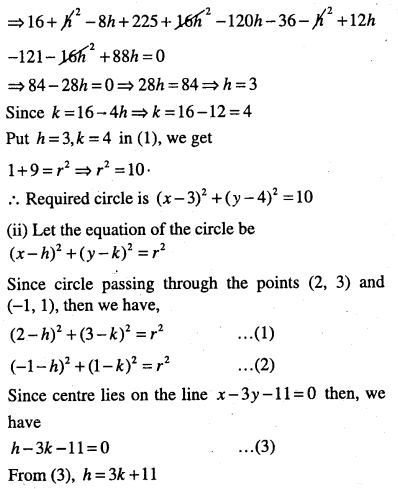

![]()
Question 8.
Find the equation f the circle with radius 5 whose centre lies on x-axis and passing through the point (2,3).
Answer:

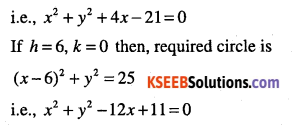
Question 9.
Find the equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes.
Answer:

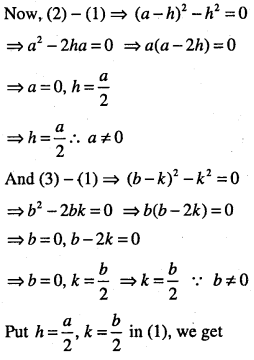

![]()
Question 10.
Find the equation of the circle with centre (2,2) and passes through the point (4,5).
Answer:


Question 11.
Does the point (-2.5, 3.5) lie inside, outside or on the circle x2 + y2 = 25?
Answer:

Parabola:
Question 1.
Define parabola.
Answer:
A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane. OR Parabola is the locus of a point which moves in a plane such that its distance from a fixed point is equal to its distance from a fixed line. The fixed point is called focus and fixed line is called directrix of the parabola.
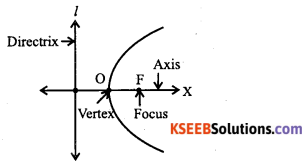
Question 2.
Write the standard equations of parabola and their respective graphs
Answer:
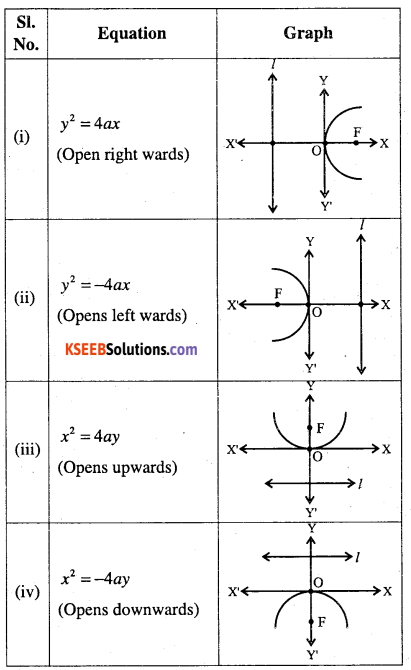
Note: Parabolas are symmetrical about co-ordinate axes.
![]()
Question 3.
Derive the equation of a parabola in the form y2 =4ax
Answer:
Let F be the focus and l be the directrix. Draw FM perpendicular to l. Take the mid-point of FM as origin O and introduce the coordinate axes shown in the figure. Let the distance between the directrix and focus be 2a. (i.e., FM = 2a) Then |OF| = |OM| = a and F = (a,0) and equation of directrix is x = -a i.e., x + a =0.
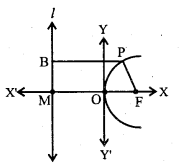

Question 4.
Define latus rectum of a parabola and find the length of the latus rectum of the parabola y2 = 4
Answer:
Definition: Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola.
Length of latus rectum of y2 = 4ax:
By definition of parabola, AF = AC . But
FM = 2a = AC
∴ AF – 2a
Since the parabola is symmetric with respect to x-axis then
AF = FB = 2a
By definition, AB = latus rectum
∴ AB = AF + FB = 2a + 2a = 4a
∴ Length of latus rectum = 4a.
Note: Observations: (Useful for solving exercise) Vertex = (0, 0)
| Equation | Axis | Focus | Directrix | LR |
| y2 = 4ax | x-axis | (a,0) | x + a = 0 | 4a |
| y2 =-4ax | x-axis | (-a, 0) | x-a = 0 | 4a |
| x2 = 4ay | y-axis | (0 ,a) | y + a = 0 | 4 a |
| x2 – 4ay | y-axis | (0 -a) | y – a = 0 | 4 a |
![]()
Question 5.
Find the coordinates of the focus axis of the parabola, equation of the directrix and length of latus rectum.
(i) y2 = 8x
(ii) y2 =12x
(iii) y2 = 10x
(iv) y2 = – 8x
(v) x2 6y
(vi) x2 = – 16y
(vii) x2 = -9y
(viii) 3y1 = 12x
(ix) 3x2 = -4y
(x) 2y2 = -6x (viii, ix, x are not in exercise)
Answer:
Given (i) y2 = 8x. This is of the form
y2 = 4 ax
∴ 4a = 8 ⇒ = 21
We have, Focus: (a,0) = (2,0)
Axis: x-axis
Equation of directive: x + a = 0 i.e., x + 2=0
Length of latus rectum: 4a = 4(2) =8
(ii) Given: y2 = 12x
Form: y2 = 4ax
∴ 4a = 12 ⇒ a = 3
We have,
Focus : (a,0)=(3,0)
Axis : x – axis
Directrix: x + a=0 i.e., x + 3 = O
Latus rectum: 4a = 4(3) = 12
(iii) Try yourself.
\(F=\left(\frac{5}{2}, 0\right), x \text { -axis, } x+\frac{5}{2}=0,10\)
(iv) Given y2 = – 8x
Form: y2 = – 4ax
4a = 8 ⇒ a=2
We have,
Focus: ( – a,0) = ( – 2,0)
Axis: x-axis
Directrix : x – a = 0 ⇒ x + 2 = 0



![]()
Question 6.
Find the equation of the parabola that satisfies the give conditions.

(I)
(i) Vertex (0, 0) passing through (2, 3) and axis is along x-axis.
(ii) Vertex (0, 0) passing through (5, 2) and symmetrix with respect toy – axis.
(iii) Symmetric about y-axis and passing through the point (2, -3).
Answer:
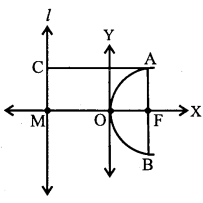
I. (i) Given that
Focus = (2, 0), Directrix : x = – 2
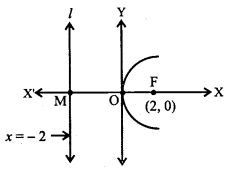
Since (2, 0) lies on the positive then axis of the required parabola is x-axis!
∴ By data, required parabola is
y2 – 4ax ………… (1)
We have, focus = (a,0) = (2,0) (given)
∴ a = 2
∴ (1) = y2 = 4(2)x
⇒ y2 = 8x is the required parabola.
(ii) y2 = 24x (Try yourself)
(iii) Given, F= (0,- 3), l : y =3
Since F lies on the negative y-axis then axis of the parabola is y-axis.
By data, required parabola is
x2 = – 4ay …………. (1)
But F = (0, – 3) = (0, – a)
∴ a = 3
(1) = x2 = -4(3)y ⇒ x2 = – 12y
is the required equation of the parabola.
(II)
(i) Given that, vertex = (0, 0) and focus = (0, 2)
Since focus lies on the positive y-axis then the required equation of the parabola is
x2 = – 4ay ……………….(1)
Since, focus = (0,2) = (0,a) ∴ a = 2
∴ (1) ⇒ x2 = – 4(2)y
⇒ x2 = – 8y is required equation
(ii) Given that, vertex = (0, 0) and focus = (3,0)
Since focus lies on the positive x-axis, then the required equation of the parabola is
y2 =4ax ………………. (1)
Since focus = (3, 0) = (a, 0) a = 3
(1) ⇒ y2 = 4(3)x ⇒ y2 = 12x
(iii) Given that, vertex = (0, 0) and focus = (-2, 0)
Since focus lies on the negative x-axis, then the required equation of the parabola is
y2 = -4ax ………………. (1)
Since focus = (-2, 0) = (-a, 0) a- 2
(1) ⇒ y2 = -4(2)x =5.1
y2 = -8x
![]()
(III)
(i) Given that, Axis: x – axis
Vertex = (0, 0) and point = (2, 3)
Since (2, 3) lies in the first quadrant and axis is x-axis, then the required equation of the parabola is
y2 =4ax ………………. (1)
Since (1) passes through the point (2, 3) then, we have
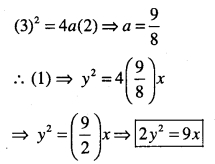
(ii) Given: V = (0, 0), Axis: y-axis, point = (5, 2) Since the point (5, 2) lies in the first quadrant and axis is y-axis then, the required equation of the parabola is
x2 =4ay ………………. (1)
Since (1) passing through the point (5, 2) then, we have
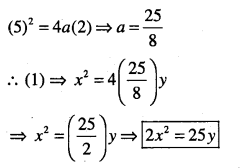
(iii) Given: Axis: y-axis, point = (2,-3)
Since (2, -3) lies in the fourth quadrant and axis is y-axis then, the required equation of the parabola is x2 = -4ay ………………. (1)
Since (1) passing through the point (2, -3) then, we have

Ellipse
Question 1.
Define ellipse.
Answer:
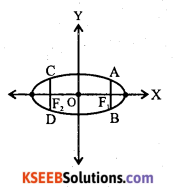
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant. The two fixed points are called foci.
Points to be noted:
- The mid point of the line segment joining the foci is called centre of the ellipse.
- The line segment through the foci is called the major axis.
- The line segment through the centre and perpendicular to the major axis is called minor axis.
- The ends points of major axis are called vertices of the ellipse.
- Length of major axis is 2a
- length of minor axis is 2b
- Distance between the foci is 2c
- Relationship between semi-major axis, semiminor axis and distance of the focus from the centre of the ellipse is a2 =b2 + c2 i.e., \(c=\sqrt{a^{2}-b^{2}}\)
![]()
Question 2.
Define eccentricity of an ellipse.
Answer:
The eccentricity of an ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse. Eccentricity is denoted by \(e.e=\frac{c}{a} \)(Here c <a ∴ e< 1)
Question 3.
Write standard equations of an ellipse and their respective graphs.
Answer:
Standard equations of an ellipse are \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
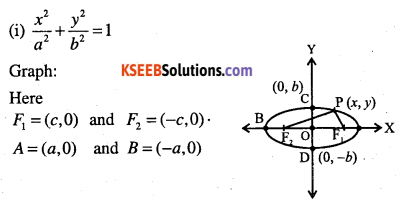
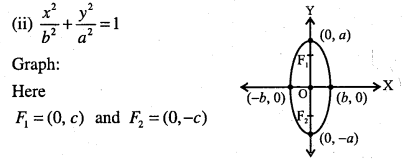
![]()
Question 4.
Derive the equation of an ellipse in the form
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Answer:
Let F1 and F2 be the
foci and ‘O’ be the midpoint of F1F2
Let ‘O’ be the origin and line from ‘O’ <through F1 and F2 be x-axis and through ‘O’ perpendicular to the x-axis be the y-axis.
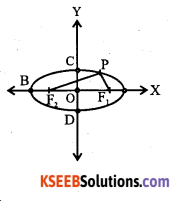
Let F1 =(c,0) and F2 =(-c,0)
Let P(x, y) be any point on the ellipse such that the sum of the distances from P to the two foci be ‘2a’. i.e., PF1 + PF1=2a ………………… (1)
By distance formula, we have

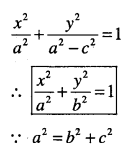
![]()
Question 5.
Define latus rectums of an ellipse and find the length of the latus rectum of the ellipse
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Answer:
Definition: Latus rectum of an ellipse is a line segment perpendicular to Q the major axis through any of the foci and whose ends points lie on the ellipse. In the figure, AB and CD are latus rectum. Let the length of AF1 be l . Then A = (c,l)


Question 6.
Find the coordinates of foci, the vertices, length of major and minor axes, the eccentricity and the latus rectum of the ellipse.
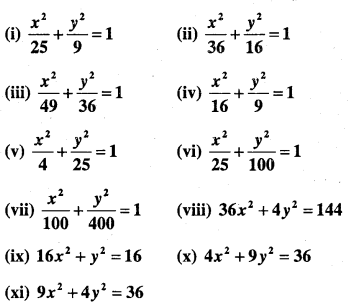
Answer:








![]()
Question 7.
Find the equation for the ellipse that satisfies the given conditions:
(i) Vertices (±5,0), foci (±4,0)
(ii) Vertices (0,±13), foci (0,±5)
(iii) Vertices (±13,0), foci (±5,0)
(iv) Ends of major axis (±3,0) ends of minor axis (0,±2)
(v) Ends of major axis \((0, \pm \sqrt{5})\), ends of minor axis (±1,0)
(vi) Length of major axis 26, foci (±5,0)
(vii) Length of major axis is 20, foci (0,±5)
(viii) Length of minor axis is 16, foci (0,±6)
(ix) Foci (±3,0), a = 4
(x) b = 3, c = 4 centre at the origin; foci on the x-axis.
(xi) Centre (0, 0), major axis on the y-axis and passes through the point (3,2) and (1,6)
(x) Major axis on the x-axis and passes through the points (4,3) and (6,2).
Answer:
(i) Given vertices Vertices (±5, 0), foci (±4,0)
We have, vertices = (±a,0) = (±5,0) a = 5
And foci = (±c, 0) (±4,0) c = 4
We have a2 =b2 + c2
i.e., b2 =a2 -c2
=(5)2 -(4)2 =25-16 = 9
i.e., b2 = 9 ⇒ b = ±3
∴ a = 5 and b = 3
∴ Required equation of ellipse is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \quad( \text { foci lie on } x \text { -axis })\)
\(\text { i.e., } \sqrt{\frac{x^{2}}{25}+\frac{y^{2}}{9}=1}\)
(ii) Given Vertices = (0,±13), foci = (0,±5)
Since foci lie on y-axis, then required equation of the ellipse is \(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\) …………(1)

(iii) Given : Vertices = (±13,0), foci= (±5,0)
Since foci lie on the x-axis, then required equation of the ellipse is
\(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\)
Since, vertices = (±a, 0) = (±13,0) ∴ a =13

(iv) Given: Ends of major axis (±3,0) ends of minor axis (0,±2)
i.e., (± a,0) = (±3, 0) and (0, ±b) = (0,±2)
∴ a = 3 and b = 2
Required equation of the ellipse is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \text { i.e., } \frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)
![]()
(v) Given: Ends of major axis \((0, \pm \sqrt{5})\), ends of minor axis (±1,0)
Since ends of major axis lie on the y-axis, then required equation of the ellipse is,

(vi) Given: Length of major axis 26, foci (±5,0) Since, foci lie on the x-axis, t hen required equation of the
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
We have, length of major axis =2a = 26 (given)
and foci = (±c, 0) = (±5,0)
∴a=\(\frac{26}{2}=13\)
and foci = (±c, 0) = (±5,0)
∴ c = 5

(vi) Given: Length of minor axis is 16, foci (0,±6)
Since, foci lie on the y-axis, then required equation of the ellipse is

![]()
(viii) Given: Length of minor axis is 16, foci (0,±6)
Since, foci lie on the y-axis, then required equation of the ellipse is
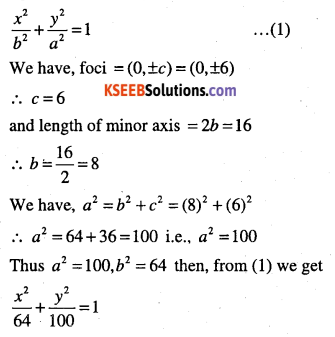
(ix) Given: Foci (±3,0), a = 4
Since foci lie on the x-axis, then the required equation of the ellipse is
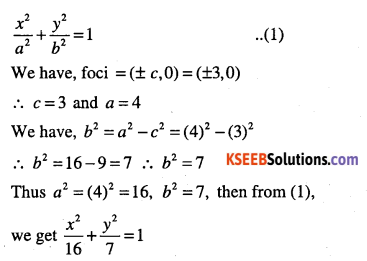
(x) Given: b = 3, c = 4 a = (0,0)
Since foci on the x-axis, then required equation of the ellipse is,
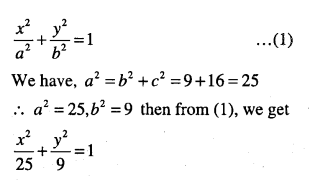
(xi) Given: Centre (0, 0), axis : y-axis
Since major axis is on the y-axis then, required equation of the ellipse is,
\(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\)
Since (1), passes through the point (3, 2) and (1,6) then, we


![]()
Hyperbola:
Question 1.
Define hyperbola.
Answer:
A hyperbola is the set of all points in a plane, the difference of whose distance from two fixed points in the plane is a constant.
Note: Observations
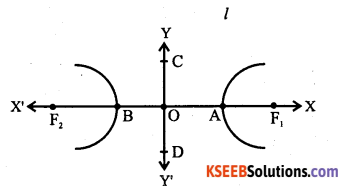
(i) The two fixed points F1, F2 are called foci of the hyperbola.
(ii) The mid-point of the line segment joining the foci is called centre of the hyperbola.
(iii) The line through foci is called transverse axis and the line through the centre and perpendicular to the transverse axis is called conjugate axis
(iv) The points at which the hyperbola intersects the transverse axis are called vertices of the hyperbola.
(v) Distance between foci is denoted by 2c, distance between vertices by 2a, and define the quantity b as \(b=\sqrt{c^{2}-a^{2}} \text { i.e., } \sqrt{b^{2}=c^{2}-a^{2}}\)
(vi) Length of transverse axis = 2a
Length of conjugate axis = 2b
(vii) Eccentricity = \(e=\frac{c}{a}(\text { Here } c \geq a)\)
∴ Eccentricity is never less than 1.
Standard equation of hyperbola and their graphs:
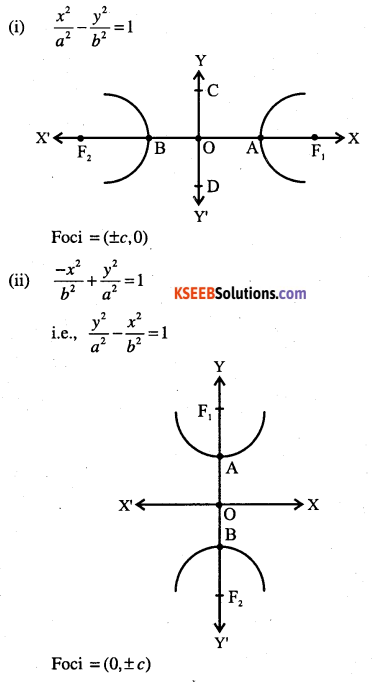
Question 2.
Derive the standard equation of the hyperbola in the form
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
Answer:
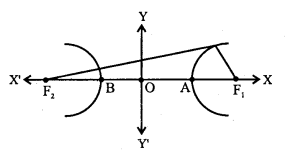
Let F1 and F2 be the foci and ‘O’ be the midpoint of line segment F1F2.
Let ‘O’ be the origin and the line through ‘O’, F1 and F2 be the x-axis. The line through O, perpendicular to the x-axis be the y-axis.
Let F1= (c,0) and F2 = (-c,0)
Let P = (x,y) be any point on the hyperbola such that the difference of the distances from P to the
F1 and F2 be 2a.
i.e., PF2-PF1=2a
Using the distance formula, we have

Length of latus rectum \(=\frac{2 b^{2}}{a}\)
Note: A hyperbola in which a = b is called an equilateral hyperbola.
![]()
Question 3.
Define latus rectum of hyperbola.
Answer:
Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola.
Question 4.
Find the coordinates of the foci, vertices, eccentricity, length of transverse axis and conjugate axis and length of latus rectum of the hyperbola.
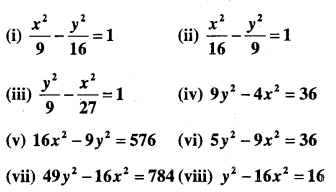
Answer:






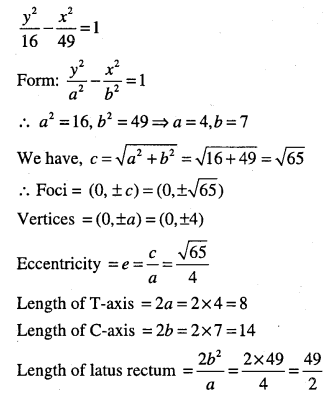

![]()
Question 5.
Find the equations of the hyperbola satisfying the given conditions.
(i) Vertices (±2,0, foci = (± 3,0)
(ii) Vertices = (0, ± 5), foci = (0, ± 8)
(iii) Vertices = (0, ± 3), foci =(0, ± 5)
(iv) Foci = (± 5,0) length of transverse axis = 8
(v) Foci = (0, ±13), length of conjugate axis = 24.
(vi) Foci = \((\pm 3 \sqrt{5}, 0) \), length of latus rectum = 12
(vii) Foci = (± 4,0) length of latus rectum -12
(viii) Foci =\((\pm 7,0), e=\frac{4}{3}\)
(ix) Foci = \((0, \pm \sqrt{10}) \)passing through (2,3)
(x) Foci = (0, ±3) vertices \(=\left(0, \pm \frac{\sqrt{11}}{2}\right)\)
(xi) Foci = (0, ± 12), length of latus rectum = 36.
Answer:
(i) Given, Vertices (±2,0, foci =(±3,0)
Since foci lie on the x-axis then the equation of the hyperbola is of the form
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \ldots(1)\)
We have,
vertices = (±a, 0) = (±2, 0) ∴ a =2
Also foci = (± c,0) = (±3,0)∴ c = 3
Since c2 = a2 +b2
∴ b2 =c2 – a2 = (3)2 – (2)2 =9-4 = 5
∴ (1) \(\Rightarrow \frac{x^{2}}{4}-\frac{y^{2}}{5}=1\)
(ii) Given Vertices = (0, ± 5), foci = (0, ± 8)
Since foci lie on the y-axis then the required equation of the hyperbola is of the form

(iii) \(\frac{y^{2}}{9}-\frac{x^{2}}{16}=1\) (Try yourself)
(iv) Given foci = (± 5, 0) T-axis = 8
Since, foci lie on the x-axis then the required equation of the hyperbola is of the form 2
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \) We have,
foci =(±c,0) = (±5,0) ∴ c = 5
Length of T-axis = 2a = 8 ∴ a = 4
Since b2=c2-a2 =25-16 = 9
(v) Given foci = (0, ±13), c-axis length = 24.
Since foci lie on the y-axis then the equation of the hyperbola is of the form

![]()
(vi) Given foci \(=(\pm 3 \sqrt{5}, 0) \) length of LR = 8
Since foci lie on the x-axis then the required equation of the hyperbola is of the form



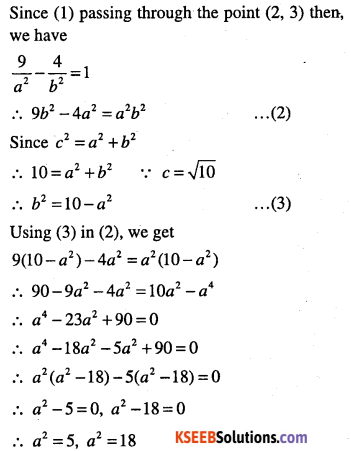

Miscellaneous examples
Question 1.
If a parabolic reflector is 20 cm in diameter and 5 cm deep find the focus.
Answer:
Given: AB = 20 cm, OC =5 cm
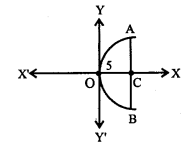
∴ AC – BC = 10 cm (curve is symmetric)
∴ A = (5,10), B = (5, – 10), C = (5, 0)
Let the equation of the parabola be
y2 =4ax
Since A (5, 10) lies on (1), then we have,
(10)2 = 4a(5)
∴100 = 20 a ∴ a =5
∴ Focus = (a, 0) = (5, 0) = c, the mid point of the diameter.
i.e., Focus of the reflector is at the mid point of the given diameter.
![]()
Question 2.
An arch is in the form of a parabola with its axis vertical. The arch is 10 m in high and 5 m wide at the base. How wide is it 2m from the vertex of the parabola?
Answer:
Given that AB = 5m, OC = 10m OD = 2m
Clearly, AC = CB = = \(\frac{5}{2} \)because the curve is symmetric about y-axis.


Question 3.
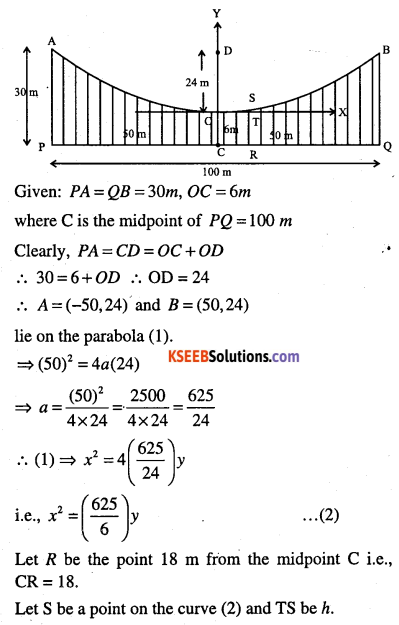
The cable of a uniformly loaded suspension bridge hands in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
Answer:
Cable is in the form of an upward parabola, its equation is
x2 = 4 ay ……………………. (1)

![]()
Question 4.
An arch is in the form of a semi ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.
Answer:
Equation of the arch be

Required height of the arch at a point Q, 1.5 m from one end A is 1.56 m.
![]()
Question 5.
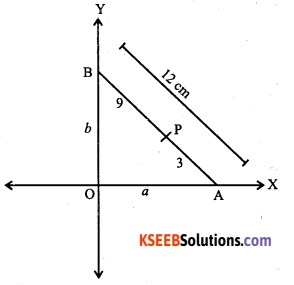
A rod of length 12 cm moves with its ends always touching the co-ordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.
Answer:
Let AB = 12 cm be the rod at any position meet x-axis at A (a, 0) and y-axis at B (0, b).

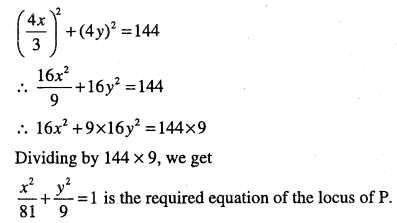
Question 6.
Find the area of the triangle formed by the line joining the vertex of the parabola jc2 = 12y to the ends of its latus rectum.
Answer:

![]()
Question 7.
A man running a race source notes that the stun of the distances from the two flag posts from him is always 10 m and the distance between the flag posts is 8 m. Find the equation of the posts traced by the man.
Answer:
Required equation is of the form
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

Question 8.
An equilater triangle is inscribed in the parabola y2 = 4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
Answer:
Given: ΔAOB is an equilateral triangle inscribed in the parabola y2 = 4ax,
whose vertex is ‘O’


![]()
Question 9.
The focus of a parabolic mirror as shown in the figure is at a distance of 5 cm from its vertex. If the mirror is 45 cm deep, find the distance AB.
Answer:
From the given figure, we have equation of the parabolic mirror is
y2 = 4ax ……………..(1)
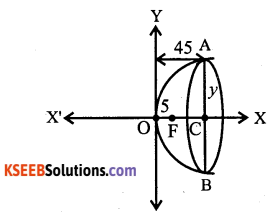
Given: OF =5, F be the focus of (1)
Since F = (a, 0) = (5,0) ∴ a = 5
And OC = 45 = Depth of the mirror.
A = (45,y) and B = (45,-y)
We have, x = 45, y = y and a = 5 then equation (1) gives,
y1 =4 x 5 x 45 = 900 y = ± 30
AB = 2y = 2 x 30 = 60 cm
Question 10.
A rod AB, 15 cm rests in between two co-ordinate axes such that A lies on x-axis and B lies on y-axis. A point P (or, y) is a point on AB such t hat AP = 6 Show that the locus of P is an ellipse.
Answer:
Given: AB = 15, AP = 6 and PB = 9

Validating statements :
Validity of a statement (Truthfulness of a statement) can be established by the following methods.
- Direct method
- Contradiction method
- Contrapositive method
- Counter example method
Note: In mathematics, counter examples are used to disprove the statements.
![]()
Question 1.
Show that the statement p: “If x is a real number such that x3 + 4x = 0, then x is O” is true by
(i) Direct method,
(ii) Method of contradiction
(iii) Method of contrapositive.
Answer:
Given that, p: “If x is a real number such that x + 4x = 0, then x is O”.
(i) Direct method:
Let x3+4x = 0, x ∈ R
⇒ x(x2 + 4) = 0, x ∈ R
⇒ x = 0 ∵ x2 + 4 = 0
⇒ \(x=\pm \sqrt{-4} \notin R\)
⇒ p is a true statement.
(ii) Method of contradiction:
Let x ≠ O, x ∈ R
i.e., Let x be a nonzero real number
⇒ x2 > 0 (y square of non-zero real number is always positive)
⇒ x2 + 4 > 0 + 4
⇒ x2+ 4 > 4 x2 + 4 ≠ 0
⇒ x(x2 +4) ≠ 0
⇒ x3 + 4x = 0, which is a contradiction for x3 + 4x = 0 .
Hence x = 0 ⇒ p is true.
(iii) Method of contrapositive
∵ p: “If x is a real number such that x3 + 4x = 0, then x is O”.
Let q : “x is a real number and x3 + 4x = 0″ r:”x is 0″
∴ p is q ⇒ r
Its contrapositive is ~ r ⇒ ~ q
i.e., “I-x is non-zero real number, then x3 + 4x is also non-zero”.
Now, x ∈ R x 0
⇒ x2 >0
⇒ x2+4>0 + 4
⇒ x2 + 4 > 4
⇒ x2 + 4 ≠ 0
⇒ x(x2+4)≠ 0
⇒ x3 + 4x ≠ 0
i.e., ~ r ⇒~ q is always true.
Hence q ⇒ r is true, i.e., p is true.
![]()
Question 2.
Show that the statement “For any real numbers a and b, a2 = b2 implies that a = b” is not true by giving counter example.
Answer:
Let a = 2 and b = – 2, then a and b are real numbers and a2 = b2
∵ a2 = (2)2 = 4, b2 = (-2)2 = 4
a2 = b2 but a ≠ b (∵ 2 ≠ – 2)
Hence, a,b ∈ R and a2 = b2
⇒ a = b is not true.
Question 3.
Show that the following statement is true by the method of contrapositive, p : If x is an integer and x2 is even, then x is also even.
Answer:
Let q : x ∈ I and x2 is even
r: x is even integer.
∴ Given p is q ⇒ r
Its contrapositive is ~ r ⇒ ~ q.
Now, ~ r: x is not an even integer i.e., ~ r
⇒ x is an odd integer.
⇒x = 2n + 1 for n ∈ 1
⇒ x2 = (2n +1)2 = 4n2 + 4n +1 = 2(2n2 + 2n) +1
⇒ x2 is an odd integer.
⇒ x2 is not an even integer.
⇒ ~q
∴ ~ r ⇒ ~ q is true.
Hence q ⇒ r is true, i.e., p is true.
![]()
Question 4.
By giving counter example, show that the following statements are not true.
(i) If all the angles of a triangle are equal, then the triangle is an obtuse angled triangle.(ii) The equation x2 – 1 = 0 does not have a root lying between 0 and 2.
Answer:
(i) Let PQR be triangle in which P = 60°, Q = 60°, R = 60°, then the triangle PQR is not an obtuse angled triangle. ∴ Given statement is not true.
(ii) Clearly x2 -1 = 0 has x = 1 as one of the root lies between 0 and 2.
∴ Given statement is not true.